一卷胶带纸有多长
2018-08-08谭亚鹏蒋守成
谭亚鹏 蒋守成
【教学目标】
1.探寻“一卷胶带纸有多长”问题解决办法,认识长度单位“微米(μm)”和“码(yd)”。
2.在经历提出问题、解决问题的过程中提升教师的独立思考、自主探索和合作探究能力的提升。
3.在运用数学知识和策略解决问题的过程中,体会数学与生活的联系,增强学生应用相关知识点解决简单实际问题的能力和意识。
【教学重、难点】
在不同解决方法中相互印证,体会转化策略的价值。
【教学流程】
课前谈话
师:今天是咱们第一次见面,老师想玩个小游戏来增加咱们之间的默契,(出示1张A4纸)你觉得这张A4纸最多能被对折多少次?
生1:10次。
生2:15次。
生3:……
师:刚才同学们说了很多可能,但这些只是我们的……
生:猜想。
师:然后我们就要来……
生:验证!
师:老师想请一名男生和一名女生上台折一折、比一比。
(结果:男生和女生都对折了6次)
师:同学们,刚才我们面对“一张A4纸最多能被对折多少次”这个问题时,先提出了自己的猜想,又进行了验证,其实这就是一次小小的数学探究。
【评析:提出“一张A4纸最多能被对折多少次”这个问题,一方面极大的吸引了学生的注意力,调动起学生的课堂氛围;另一方面让学生经历一次数学探究,明确数学探究的过程要经历猜想—验证—结论—应用的过程。】
一、在问题中思考,激发学习兴趣
师:这节课,谭老师就要和同学们一起进行一次数学研究。今天我们要研究的主题是……
生:一卷胶带纸有多长?
师:想过这个问题吗?
生:没有……
二、在探究中理解,沟通知识体系
1.交流讨论,明确基本思路
师:课前老师给大家发了这样的一卷胶带纸,根据平时使用胶带纸的经验,你觉得这卷胶带纸的长度会是多少米?
生1:20米。
生2:35米。
生3:40米。
生4:6米。
师:同学们的答案很多,但這些都只是我们的猜想,要想知道一卷胶带纸到底有多长,我们还需要……
生:验证!
师:是的,那你有办法知道一卷胶带纸的长度吗?把你的想法在四人小组里讨论讨论。
生:可以把胶带纸彻底拉开,拿尺子量一下!
师:好的,这种方法有些原始,很实用,但不方便且浪费。
生:可以先算出一圈胶带纸有多长,再乘有多少圈!
师:这种方法可以吗?
生1:我觉得不行,因为胶带纸有多少圈我们没有办法知道.
生2:而且胶带纸每一圈的周长都不一样。
师:看来,同学们遇到了一些困难,不着急,给大家些提示。让我们拿起桌面上的胶带纸,从侧面看,胶带纸是什么形状的?
生:圆环。
师:如果把一卷胶带纸展开一部分,展开的这个部分是什么图形?
生:长方形!
师:可老师觉得它像一条线段,你们怎么说它是一个长方形呢?
生:因为胶带纸是有厚度的!
师:的确,虽然一层胶带纸很薄,但它也是有厚度的,所以展开部分是一个长方形。
师:再展开一些,得到的又是一个什么图形呢?
生:长方形!
师:如果把这卷胶带纸彻底展开,它又是什么形状呢?
生:还是长方形!
师:谁能说一说,这个长方形的长和宽分别相当于胶带纸的什么?
生:长方形的长相当于胶带纸的长度,长方形的宽相当于胶带纸的厚度。
师:你们同意他的想法吗?还有谁能像他这样再来说一说?
(多名学生举手说)
师:比较胶带纸展开前的圆环和展开后的长方形,认真思考,在这个过程中,什么变了?什么没有变?
生1:形状变了,长度不变,厚度也不变。
生2:面积也没有变!
师:观察得真仔细,也就是说,展开后的长方形的面积应该等于展开前圆环的面积,我们可以用“圆环的面积=长方形的面积”这个等式来表示。
师:研究到这里,对于解决胶带纸有多长这个问题,你有什么新的想法了吗?
生1:用大圆的面积剪去小圆的面积等于长方形的面积
生2:“大圆面积-小圆面积=胶带纸的长度×胶带纸的厚度”。
生3:可以先算出圆环的面积,再除以胶带纸的厚度,就可以得到胶带纸的长度!
2.实践操作,搜集相关数据
师:结合这一个数量关系,你觉得我们还需要测量哪些数据?
生:需要测量大圆和小圆的半径,还有一层胶带纸的厚度。
师:大圆和小圆的半径比较好量,可一层胶带纸很薄,用尺子直接测量厚度的话比较困难,该怎么办呢?
(生露出不解的表情。)
师:回想一下,我们低年级是怎样测量过一张纸的厚度的?
生:我们可以先测量100层胶带纸的厚度,再用这个厚度除以100计算出每一层的厚度。
师:这位同学的想法非常棒,不过数出100层花费的时间略微有点长,可以换一个方式,同学们看到老师手上有一段胶带纸,老师把它对折,有几层了?
生:2层。
师:继续对折呢?
生:4层。
师:再对折?
生:8层。
师:继续呢……
生:16层!
……
师:明白老师的意思了吗?那么现在老师把时间交还给你们,同桌合作,大圆半径、小圆半径,测量出胶带纸单层厚度,并记录下来。
(生合作探究数据)
师:我们请XXX同学来回报一下他们的结果!
生:大圆半径是2.3厘米,小圆半径是1.7厘米,一层胶带纸的厚度是0.00390625厘米!
师:你是怎样得出一层胶带纸的厚度的?
生:我叠了128层胶带纸,量出总厚度是0.5厘米,用0.5除以128得到一层胶带纸厚0.00390625厘米。
师:有和他一样的吗?
(部分生举手)
师:有不一样的吗?
生:我叠了64层,是0.25厘米!算出来也是0.00390625厘米。
师:为了方便大家计算,我们统一一下测量结果,大圆的半径是2.3厘米,小圆的半径是1.7厘米,一层胶带纸的厚度就看成是0.004厘米。有了数据,你会计算了吗?
生:会!
师:在研究单上计算出结果。
(生独立计算。)
师:刚才我们计算除了这卷胶带纸的长度是18.84米,接下来我们用同学们说的第一种方法实际测量来验证这个结果是否正确。我们请两组同学拉开胶带纸量一量!
(生测量)
生:量出来是17.4米,跟算出来的结果不一样!
师:怎么会不一样呢?是我们量错了?还是算错了呢?
生:不是,是我们量的胶带纸的厚度以及直径不精确!
师:是的,在测量的时候能存在一定的误差,所以导致结果不准确。如果能得到更加精确的数据,我们就能够减小这样的误差。
3.回顾反思,形成基本方法
师:同学们,回顾刚才我们解决这个问题的过程,你有什么体会?
生1:我们可以用转化的策略来解决复杂问题。
生2:遇到问题时,我们可以先提出自己的猜想,但猜想不一定正确,我们一定要去验证。
生3:……
【评析:针对学生的解决问题的办法,进行逐步剖析,层层突破,感受到解决问题的快乐,同时不仅提出问题解决问题,更重要的是让学生经历提出问题-猜想-验证的完整过程,掌握基本的數学探究方法,培养学生的应用意识和实践能力,同时通过验证明晰用数学方法进行计算时要控制造成误差的核心因素,就是半径和厚度越精确结果就越准确。】
三、在比较中选择,揭示数学信息
师:悄悄告诉大家,谭老师有一个神奇的本领,不用计算,不用测量,就能知道胶带纸的长度,想了解一下吗?
生:想!
师:由于老师买的胶带纸比较多,所以文具店的叔叔就连着纸箱一起给我了,看!就是这个,仔细观察,你有什么想说的吗?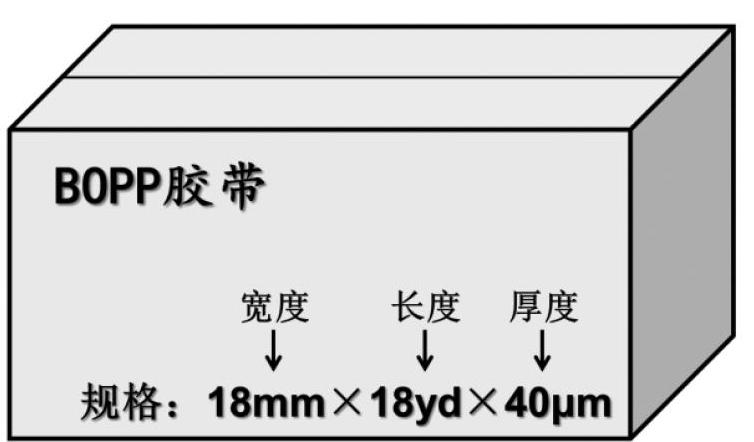
生:乘法算式中一定包含和长度有关的信息!
师:是18mm吗?
生:mm是毫米,18毫米肯定不可能是胶带纸的长度。
师:那它可能是什么?
生:胶带纸的宽度!
师:40μm,μm是什么意思?
生:微米。
师:μm是微米,1000微米是1毫米,40微米可能是胶带纸的……
生:厚度。
师:那只可能是18yd了!这里的yd又是什么单位呢?
(生疑惑)
师:yd是英制单位“码”的缩写,1码=0.9144米,18yd也就是18码的意思,18码是多少米?
生:16.4592米。
师:看来从包装上我们也能看出一卷胶带纸的长度。
【评析:让学生的目光回归生活,发现在包装袋上也能找到相关的信息,从而使学生学会用数学的眼光去观察现实世界,感受生活中的数学密码和数学基因,进一步促进学生用数学的思维去思考现实世界,用数学的语言表达现实世界】
四、在反思中提升,延展课堂价值
师:我们今天一起探究了跟胶带纸有关的问题,我们经历了先猜想再验证的过程。在验证时,我们可以通过计算,也可以通过实践活动来测量,还可以直接在包装纸上获得相关信息。其实生活中还有很多这样有趣的问题,比如一卷蚊香能烧多长时间,一个可乐瓶的容积是多少……希望同学们在生活中做个有心人,多观察,勤思考,在生活中学数学,在生活中用数学。
【评析:一节课的结束并不是学生学习的终点,而是新的起点,教师应该适时在学生心中种下一颗种子,调动起学生继续学习、探究的兴趣,有一个问题的解决到一类问题的思考,提升学生系统化结构化思考的水平。】
【作者简介】
谭亚鹏,常州市金坛区朝阳小学教科室副主任,常州市教学能手;2018年获金坛区小数基本功比赛一等奖,多次获金坛区优质课评比二等奖;多次执教省、市、区级公开课;多篇文章发表于《小学数学教师》《江苏教育报》等报刊杂志。
蒋守成,江苏省小学数学特级教师,江苏省“333工程”培养对象 ,江苏省乡村骨干教师培育站主持人,常州市名师工作室优秀领衔人,常州市中青年专业技术拔尖人才,常州市教育领军人才,金坛市首届名教师,常州市金坛区朝阳小学校长。他连续主持了4项省规划立项课题和重点资助课题,研究成果获得江苏省教学成果奖一等奖。出版了1—6年级数学读本《走进你知道吗》,在研究中他提出了小学数学主题拓展教学的主张,《江苏教育》《生活教育》《学校管理》《江苏教育报》《小学教学设计》《江苏教育新时空》《小学数学教师》等媒体进行了研究成果推广和专题报道,他应邀到上海、北京、浙江、山东、河南等26个省市自治区上数学研究课、做专题报告。
