基于小样本的非等距加速应力试验寿命预测方法

郭学军，盖晓华，刘登第

(1.南阳理工学院 a.数学与统计学院; b. 电子与电气工程学院，河南 南阳 473000;2.空军指挥学院 作战仿真研究所，北京 100097)

0 引言

加速寿命试验是一种采用较产品正常状态更加严酷的试验条件，通过在有限时间内搜集更多的产品寿命与可靠性信息，提高或预测产品寿命与可靠性的内场试验方法，主要是为了节省时间、降低费用.试验的基本思想是利用加速退化数据对高可靠长寿命产品进行可靠性评估与寿命预测.这种试验方法已被广泛地应用在可靠性要求较高行业或领域之中，尤其是航空、航天及军事等领域，多数情况下需要的样本容量较少.如何在小样本的情况下实现比较精确的外推，数据的挖掘建模技术就显得非常重要[1,2].

小样本问题的预测模型有很多种，其中灰色GM(1,1)模型就是一种典型的预测模型.它通过灰生成方式来挖掘数据的深层次信息，弱化系统的随机性，从而使紊乱的原始数据列呈现出某种规律性.由于灰色预测所需要的数据量比较少，样本分布不需要有规律性，检验方便，且预测比较准确，已成功地解决了生产、生活和科学研究中的大量实际问题.传统的GM(1,1)模型其数据序列通常是等距的，然而现实问题中有许多非等距问题.对于非等距问题，文献[3-6]分别从原始数据加权累加生成、背景值构造等方面进行了研究和探讨，并取得了一定的效果，但运用中仍有其解决不了的问题存在.

本文给出了一种新的非等距GM(1,1)模型，该模型与传统的非等距生成方式不同，在数据生成处理时，不是直接利用原始数据进行建模预测，而是通过对原始数据列取对数变换作降幅平滑处理和对背景值作相对权重的加权处理.平滑处理有利于规律的寻求和预测精度的提高.背景值加权的权重是相对距离，而不是绝对距离，可以有效地避免改变原始数据列的性质.

1 温度应力下的Arrhenius模型

以文献[7]所提供的表1数据进行非等距加速应力寿命预测.表1是某厂制造的一种新型材料，为了预测正常温度150 ℃下的寿命，采用加速应力实验得到的4个温度下的寿命数据.

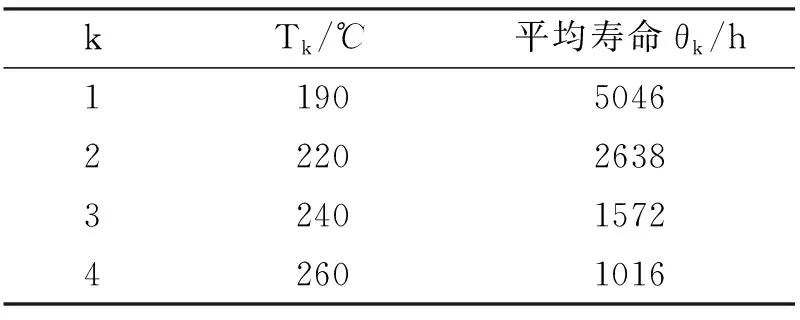
表1 4个温度下电机的平均寿命Tab. 1 Average life of motors at four temperatures

在加速寿命试验中用温度作为应力常数是常见的，因为高温能使产品(电子元器件、绝艳材料等)内部加快化学反应，促使产品提前失效.Arrhenius在1800年研究了这类化学反应，在大量数据的基础上，提出了加速模型:

θ=AeE/KT,

其中:θ是某寿命特征，如中位寿命、平均寿命等;A是一个常数，且A>0;E是激活能，与材料有关，单位是电子伏特，以eV表示;K是玻尔兹曼常数，为80617×10-5eV/℃，从而E/K的单位是温度，故又称E/K为激活温度;T是绝对温度，它等于摄氏温度加273[7].

Arrhenius模型表明，寿命特征随着温度的上升而按指数下降.对此模型两边取对数，可得

lnθ=a+b/T,

(1)

其中a=lnA,b=E/K.它们都是待定的参数.Arrhenius模型表明，寿命特征的对数是温度倒数的线性函数.根据表1中4个温度下电机加速应力实验数据，推测正常温度下(150 ℃)的寿命.

电机的寿命特征随着温度的上升而按指数下降，按照最小二乘原理可求得模型lnθ=a+b/T中的

a=-3.697 5，b=5 674.9940.

寿命预测方程为

lnθ=-3.697 5+5 674.994 0/T.

(2)

根据方程(2)可得历史数据与模拟数据的对比图，如图1所示.

根据方程(2)可得，绝对温度为423 K(150 ℃)时，寿命值为16 623.625 h.现将原始数据和预测数据作对比，并计算相对误差，结果如表2所示.从表2可以得出平均误差为3.1%.

通常情况下，以温度作为电机的加速应力的试验寿命外推常采用Arrhenius模型，但Arrhenius模型是一种物性论模型，它只有当老化过程是一个单一的化学反应，而且用作评定材料老化的性能确能反应材料老化过程中组成或结构的变化时才能应用.这说明Arrhenius模型的使用存在一定的局限性[8,9].

图1 Arrhenius模拟结果Fig. 1 Arrhenius simulation result

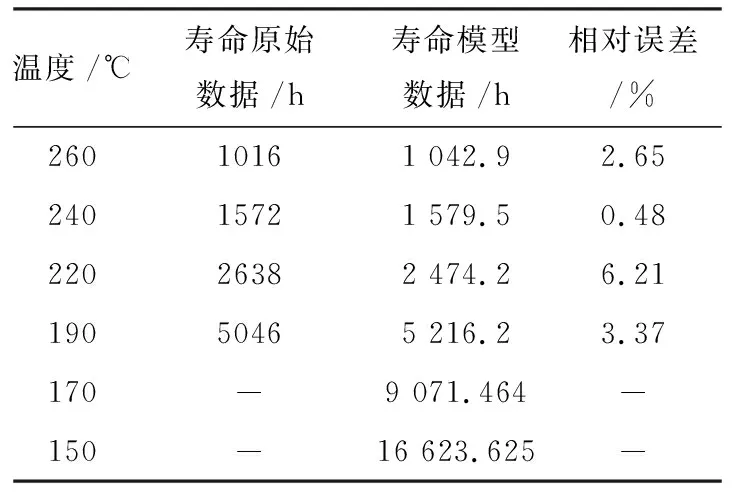
表2 电机寿命值对比表Tab. 2 Comparison of the motor life

由于灰色建模理论是应用数据生成手段来挖掘数据的深层次信息，实验数据本身就蕴含着实验过程的各种信息，这样就可以有效地避免通过单一的因素分析给整体带来的弊端.另一方面，灰色建模通过灰生成的方式弱化了系统的随机性，具有所需样本少、计算简便、检验方便等特点.基于此，为避免Arrhenius模型在电机试验寿命外推中的不足，可用灰色建模理论对电机的可靠性寿命进行预测.然而，灰色预测模型在使用过程中也会遇到检验勉强合格、不合格的状况，即使检验为合格或好，但有时也不一定满足实际要求的精度.于是灰色系统理论提出了利用残差修正模型来进行建模.而残差建模时，修正的残差系列必须是从某一项起，均大于或小于原始数据才能建模，且残差数据列不少于4个才能有效[10-12].为了有效地避免上述问题的发生，下面对灰色非等距GM(1,1)模型进行改进.

2 改进的非等距GM(1,1)模型

2.1 非等距GM(1,1)模型的基本思想

设原始数据列x(0)=(x(0)(t1),x(0)(t2),…,x(0)(tn)),其中Δti=ti-ti-1≠const,i=2,3,…,n，进行一次累加，生成数据列为

x(1)=(x(1)(t1),x(1)(t2),…,x(1)(tn)),

其中

由数据列x(1)建立GM(1，1)模型:

(3)

yn为向量:

yn=(x(0)(t2),x(0)(t3),…,x(0)(tn))T.

白化形式的微分方程的解为

k=1,2,…,n.

(4)

还原模型为

k=1,2,…,n.

(5)

2.2 改进的非等距GM(1,1)模型建模思想和步骤

传统的非等距GM(1,1)模型在对原始数据列进行累加生成时，即

所乘的Δti=ti-ti-1≠const，i=2,3,…,n是绝对距离，不是相对距离，尤其是当原始数据列(x(0)(t1),x(0)(t2),…,x(0)(tn))中的|x(0)(tk)|数值比较小，而Δti的值相对比较大时，所生成的数据x(1)(tk)列会改变原始数据列x(0)(tk)的性质，这样以x(1)(tk)为基础建立的微分方程模型就不能真实反映原始数据列的规律性，求解结果容易产生较大偏差.现对传统非等距GM(1,1)模型作改进，其步骤如下.

1)对原始数据列x(0)=(x(0)(t1),x(0)(t2),…,x(0)(tn))进行对数变换

y(0)=lnx(0)=

(lnx(0)(t1),lnx(0)(t2),…,lnx(0)(tn)).

2)作一次累加生成数据列为

y(1)=(y(1)(t1),y(1)(t2),…,y(1)(tn)),

其中

以y(1)为原始数据列建立GM(1，1)模型

(6)

3)采用加权紧邻均值法构造背景值，

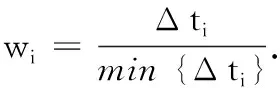
4)按最小二乘法求解得

(7)

k=1,2,…,n,

5)还原计算

(8)

k=1,2,…,n,

x(0)(tk)=ey(0)(tk),k=1,2,…,n.

(9)

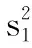
其中，

然后计算后验差比值c及小概率误差p,

c=s2/s1，

根据表3来判定模型的精度.如果模型满足后验差检验要求，即认为模型合格.

表3 灰色预测模型精度Tab. 3 Precision of grey forecast model

灰生成是灰色系统理论最显著的特点之一.改进的非等距GM(1,1)模型正是基于此思想.改进的主要目的和作用体现在两个方面：1)作对数变换的目的是对原始数据列作降幅平滑处理.2)背景值作加权乘积中的权重是相对距离，而不是绝对距离，目的是避免改变原始数据列的性质.

3 非等距加速应力算例分析

3.1 改进的非等距灰色GM(1,1)模型应用

依据表1，根据改进后灰色预测模型的式(7)和式(8)可得还原后的模型方程为

(10)

利用Matlab编程可求得模型参数为

a=-0.073 8,u=6.562 58,

得模型方程

(11)

根据式(11)可绘出预测数据与原始数据对比图，如图2所示.进而可计算各温度下预测寿命值及其相对误差，其结果如表4所示.Matlab运行结果显示p=1，c= 0.030 15，精度等级为好，并且平均相对误差为2.087%.

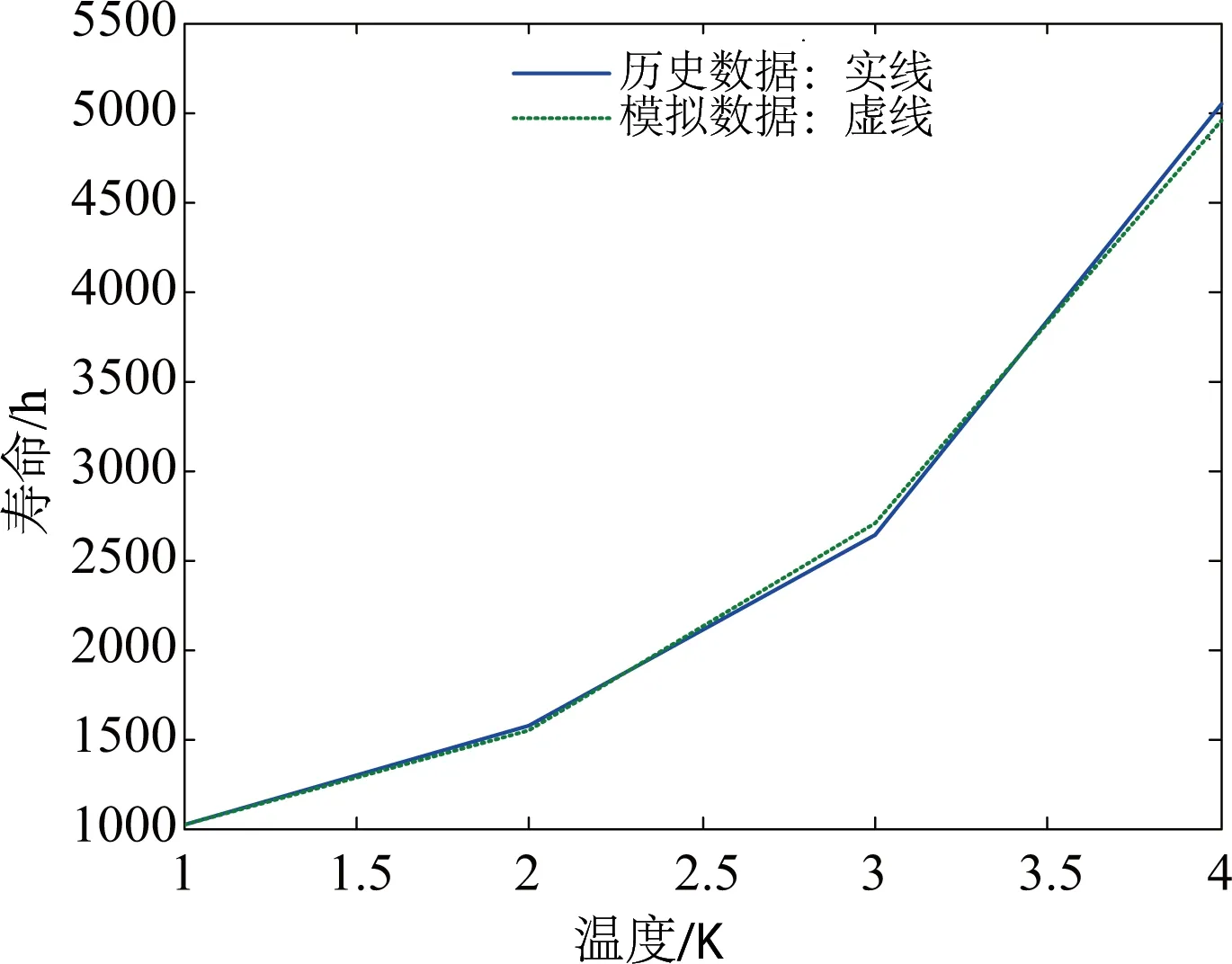
图2 预测值与原始值对比图Fig. 2 Comparison between the predicted value andoriginal value

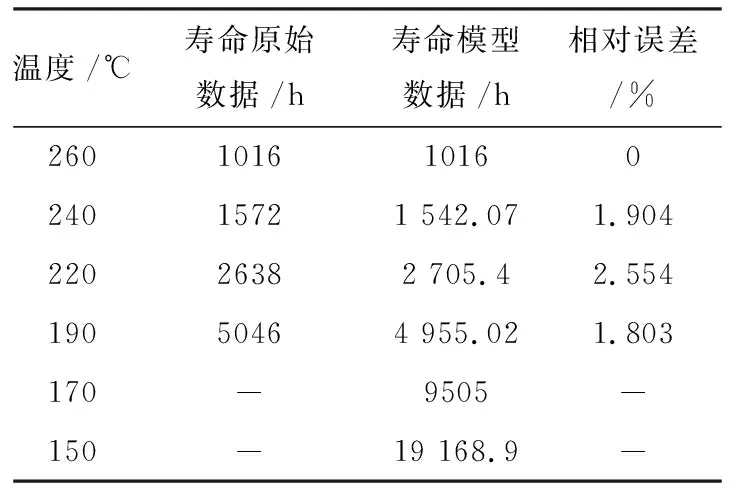
表4 改进非等距GM(1,1)模型预测值与原始值对比表Tab. 4 Comparison between improved non-equidistantGM (1,1) mode predicted data and original data

3.2 传统的非等距灰色GM(1,1)模型

依据表1，根据改进后灰色预测模型的式(7)和式(8)可得还原后的模型方程为

(12)

即，还原后的模型方程为

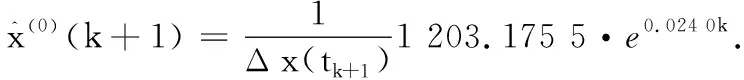
(13)

根据式(13)可绘出预测数据与原始数据对比图，如图3所示.进而可计算各温度下预测寿命值及其相对误差，其结果如表5所示.Matlab运行结果显示p=0.5，c=1.180 0，精度等级为差，并且平均相对误差为97.61%.误差太大，可见式(13)不能作为预测模型.

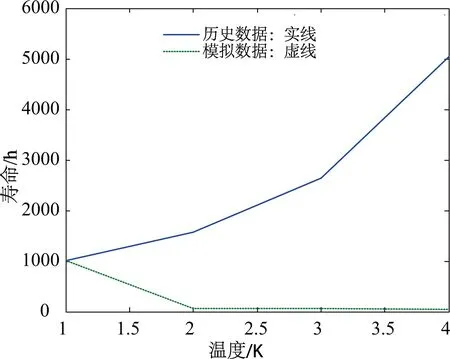
图3 预测值与原始值对比图Fig. 3 Comparison between predicted and original values

表5 传统非等距GM(1,1)模型预测值与原始值对比表Tab. 5 Comparison between traditional non equidistantGM (1,1) mode predicted data and original data

3.3 几种外推方法的比较

为了有效地说明几种方法的优劣，下面把几种模型的平均误差进行对比，其结果如表6所示.从表6可以看出，本文所给出的改进的非等距灰色GM(1,1)模型的效果好.

表6 模型平均相对误差对比表Tab. 6 Comparison of average relative error ofdifferent models

4 结论

本文所给出的改进非等距GM(1,1)模型，从基于小样本的灰色生成思想出发，进一步挖掘了灰色理论的建模优势，不仅改进了非等距GM(1,1)建模方法，而且有效地弥补了Arrhenius模型单因素建模预测的不足，在非等距加速应力预测运用方面显示出了很好的建模优势，相信对相同性质问题的解决具有参考意义.但加速应力寿命试验的外推技术是一个复杂的技术问题，本文所给出的方法仍有进一步探讨的空间.