基于症状的风机复合材料叶片疲劳可靠度及维护策略优化

黄天立，何彦杰，王宁波，张驰，陈华鹏



基于症状的风机复合材料叶片疲劳可靠度及维护策略优化

黄天立1，何彦杰1，王宁波1，张驰2，陈华鹏2

(1. 中南大学 土木工程学院，湖南 长沙，410075；2. Department of Engineering Science, University of Greenwich, Chatham Maritime, Kent, ME4 4TB, London, UK)

针对风力发电机复合材料叶片疲劳问题，基于复合材料疲劳REIFSNIDER模型推导疲劳裂缝长度扩展公式；以疲劳裂缝长度为症状指标，结合WEIBULL症状寿命模型，提出基于症状的风机复合材料叶片疲劳可靠度分析和剩余使用寿命预测方法。考虑检测和修复措施对叶片失效概率和症状可靠度的影响，采用贝叶斯方法予以修正，提出以全寿命周期维护成本为优化目标的复合材料叶片疲劳维护策略优化方法。研究结果表明：检测、修复等维护措施可有效降低叶片失效风险水平，增加症状可靠度水平；采用“检测+修复”综合维护措施比单一采用检测或修复维护措施更有效。

风机复合材料叶片；疲劳；症状可靠度；维护策略优化；贝叶斯修正

风力发电以其环境友好、可持续、成本低、建设周期短、无燃料限制等优点，成为新能源中最具有发展潜力的领域之一。风机叶片作为风力发电机最重要的部件之一，其建造成本占风力发电机总建造成本的15%~20%，其维护成本占风力发电机总维护成本的25%~30%。在恶劣的工作环境和长期风荷载耦合作用下，风机叶片常常产生疲劳破坏，从而导致整个风力发电机失效。因此，实时监测、评价风机叶片的疲劳状态并制定相应合理优化的维护策略，对提高风力发电机的发电效率、降低维护成本、预防可能发生的事故、延长其使用寿命具有重要意义[1−2]。为增强风力发电机的发电效率，风机叶片通常采用轻质、高强的纤维增强复合材料。与传统金属材料相比，虽然复合材料具有更好的抗疲劳性能，但其疲劳机理更复杂，结果离散较大。针对复合材料的疲劳问题，国内外学者提出了一些疲劳损伤模型，主要包括3种类型：1) 基于强度退化演化规律模型[3−4]，如YANG[3]提出的模型认为强度退化综合反映了材料中的损伤程度，剩余强度与载荷的循环数和加载应力水平有关；2) 基于刚度退化演化规律模型[5−6]，如宗俊达等[6]建立了拉－拉疲劳载荷作用下纤维增强树脂复合材料剩余刚度与材料损伤量及剩余寿命的复合模型；3) 基于累积损伤演化规律模型[7]。MAO等[8]通过综述复合材料的疲劳损伤模型后指出，由于问题的复杂性，目前还没有公认的适用于不同复合材料的疲劳损伤模型。如何采用现有复合材料疲劳损伤模型，通过检测/监测手段，评估风机叶片的状态并制定优化的维护策略，基于症状的可靠度理论提供了一种新的思路和解决方法。症状可靠度理论由CEMPEL等[9−10]提出并应用于发动机状态评价。结构症状可靠度可通过采集到的信息数据(如几何、材料性能、结构退化、荷载作用以及静、动力特性等)进行评价。CERAVOLO 等[11−12]采用结构自振周期作为症状指标，通过掌握其随时间的变化规律获得结构的时变症状可靠度指标，进而对桥梁结构剩余寿命进行预测。CHEN等[13−14]采用钢筋锈蚀引起的裂缝宽度和弯曲承载力作为症状指标，对退化的钢筋混凝土结构进行了症状可靠度分析及剩余寿命预测。肖南等[15−16]采用杆件应力作为症状指标，对大气腐蚀环境下的网架结构和考虑应力松弛的索穹顶结构进行了症状可靠度分析及寿命预测。本文作者针对风力发电机复合材料叶片疲劳问题，研究推导基于复合材料疲劳REIFSNIDER模型的疲劳裂缝长度扩展公式；以疲劳裂缝长度为症状指标，结合WEIBULL症状寿命模型，研究基于症状的风机复合材料叶片疲劳可靠度分析和剩余使用寿命预测方法。在讨论检测、修复措施对叶片失效概率和症状可靠度的影响并采用贝叶斯方法予以修正的基础上，研究基于全寿命周期维护成本优化目标的复合材料叶片疲劳维护策略优化方法。采用某典型海上风力发电机复合材料叶片算例验证该方法的有效性和适用性。

1 基于REIFSNIDER模型的复合材料疲劳裂缝扩展公式

1.1 复合材料疲劳损伤机理

复合材料的疲劳损伤机理比金属材料的疲劳损伤机理复杂。在循环应力或应变作用下，复合材料内部可能产生4种基本破坏形式，即基体开裂、界面脱胶、分层和纤维断裂。这些破坏形式在复合材料内部某些部位产生不可逆局部损伤，随着循环次数增加，这些局部损伤进一步扩展和增多，最终累积导致复合材料宏观力学性能发生改变，例如材料的强度或刚度减小。图1所示为REIFSNIDER等[17]基于试验观察获得的复合材料在其疲劳寿命不同时期内产生的不同损伤形式。从图1可以看出：复合材料的疲劳损伤演化规律是非线性的。在复合材料寿命前期，在材料基体内部出现许多无相互连通的裂缝，这一阶段材料损伤扩展迅速；随着荷载循环次数增加，基体内裂缝增加直至基体内裂缝密度达到饱和，这一阶段材料损伤缓慢稳定扩展；在复合材料寿命后期，在材料内部产生纤维断裂破坏，随着断裂的纤维数量逐渐增多，材料损伤再次迅速扩展，直至材料剩余强度等于外加最大荷载时，材料突然断裂。

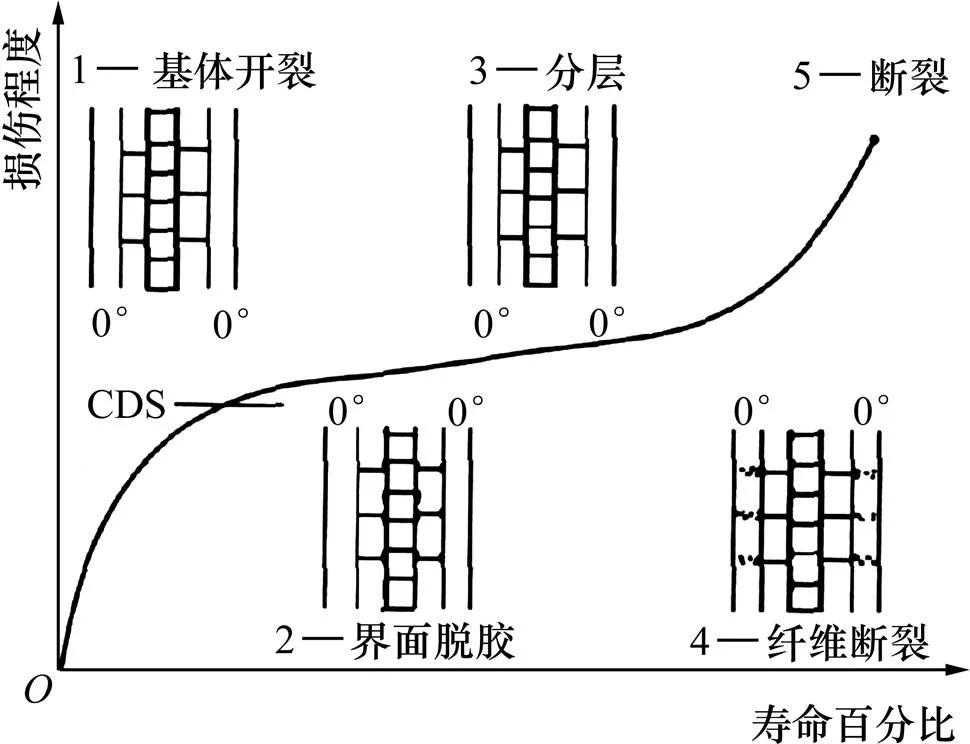
图1 复合材料疲劳损伤演化规律

1.2 复合材料疲劳裂缝长度计算

针对钢结构疲劳开裂问题，HUANG等[18]采用PARIS模型模拟其疲劳裂缝演化规律，提出了基于疲劳裂缝长度的钢桥构件优化检测维护策略。针对复合材料疲劳开裂问题，CHEN等[19]分别探讨了MINER，PARIS和REIFSNIDER这3种模型用于模拟疲劳裂缝演化规律的适用性，指出基于刚度退化的REIFSNIDER模型适用于风机复合材料叶片。REIFSNIDER等[17]基于复合材料在加载方向上的刚度退化规律，提出了一种基于刚度退化的疲劳损伤模型，即

式中：0为复合材料初始弹性模量；f为复合材料破坏时的弹性模量；()为复合材料经受次循环载荷时的弹性模量；为荷载循环次数；为材料达到疲劳寿命时的荷载循环次数；和为模型参数；()为疲劳损伤程度(当=0时，()=0，表示复合材料无疲劳损伤；当=时，()=1，表示复合材料已达到疲劳使用寿命或已疲劳失效)。

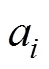
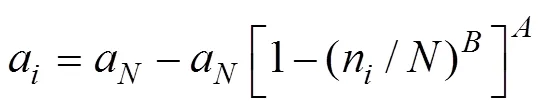
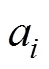
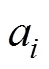
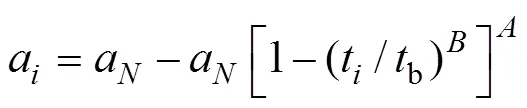
2 基于疲劳裂缝长度的复合材料结构症状可靠度

为了计算基于疲劳裂缝长度的复合材料症状可靠度，采用WEIBULL分布拟合公式(3)计算得到复合材料疲劳裂缝长度，建立WEIBULL症状寿命模型[13−14]：

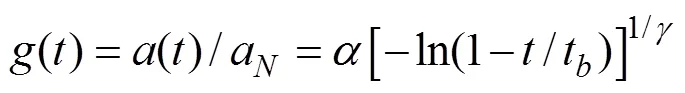
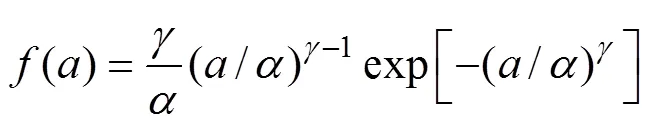
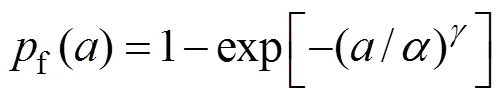
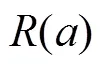
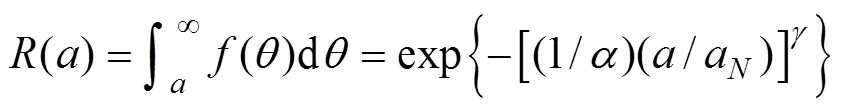
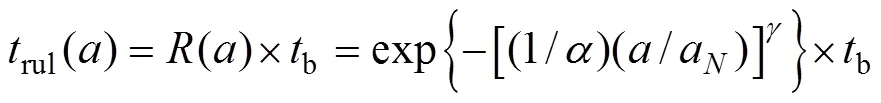
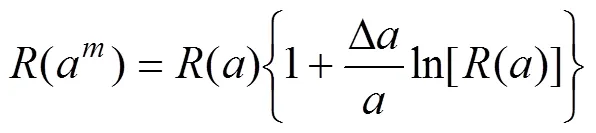
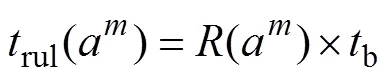
3 复合材料结构疲劳症状可靠度的贝叶斯修正

在风力发电机复合材料叶片的整个生命周期中，一般将根据计划对其进行定期或不定期检测，通过检测可为叶片的疲劳状态评估提供数据，同时这些检测数据也可用于修正结构的疲劳症状可靠度。

采用贝叶斯方法对其疲劳症状可靠度进行修正，其基本流程如下[20]。

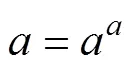
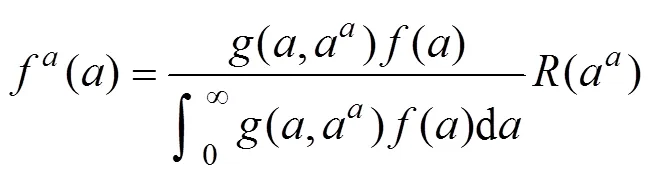
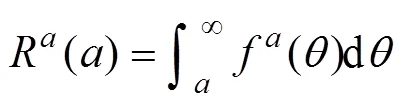
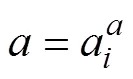
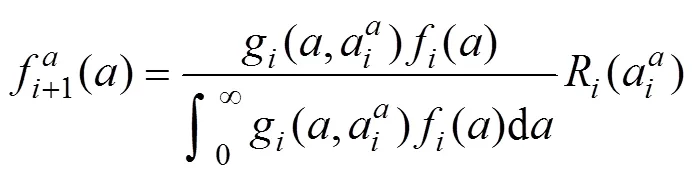
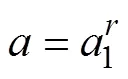
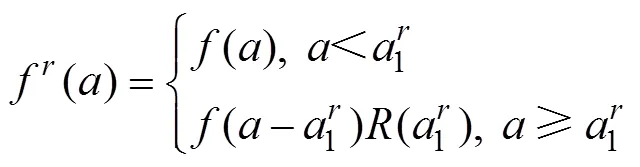
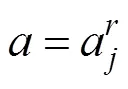
4 基于全寿命周期维护成本的复合材料结构维护策略优化

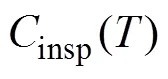
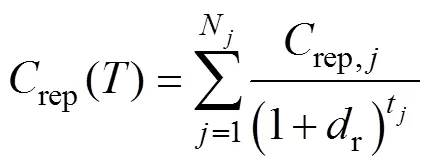
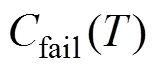
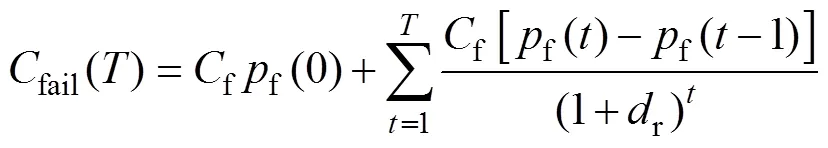
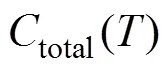
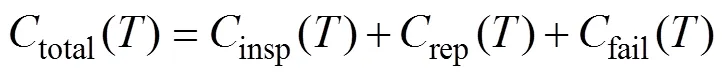
优化的检测和维护策略要求在结构安全性和维护经济性两者之间取得平衡，即在结构完成预期使用寿命的条件下，经济效益最优，即总维护成本达到最小。

5 算例分析

5.1 疲劳症状可靠度

选取某典型海上风力发电机复合材料叶片为例，叶片总长为37.5 m，根部螺栓圆直径为1.8 m，设计用于变桨控制的变速发电机，额定功率为1.5 MW。叶片采用AS4/PR500复合材料层压板构成，根据材料试验弹性模量，基于刚度退化REIFSNIDER模型公式(1)拟合得到模型参数=0.3，=0.1[19]。在一般情况下，风力发电机复合材料叶片的使用寿命为20~30 a，本文取其设计使用寿命为25 a，疲劳裂缝长度阈值a= 100 mm。

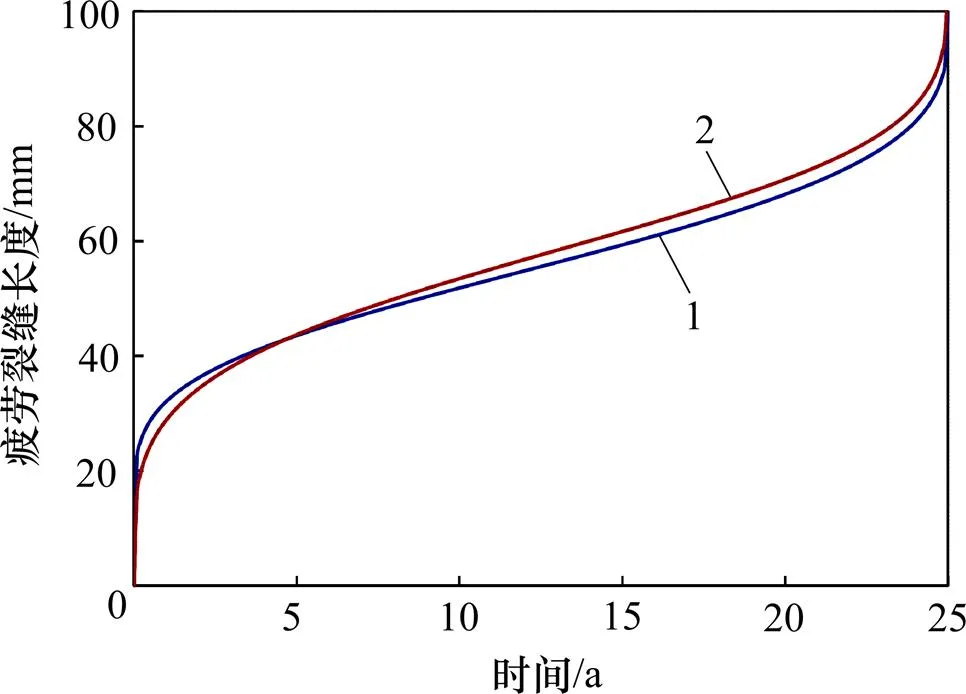
1—REIFSNIDER模型预测值；2—WEIBULL模型拟合值。

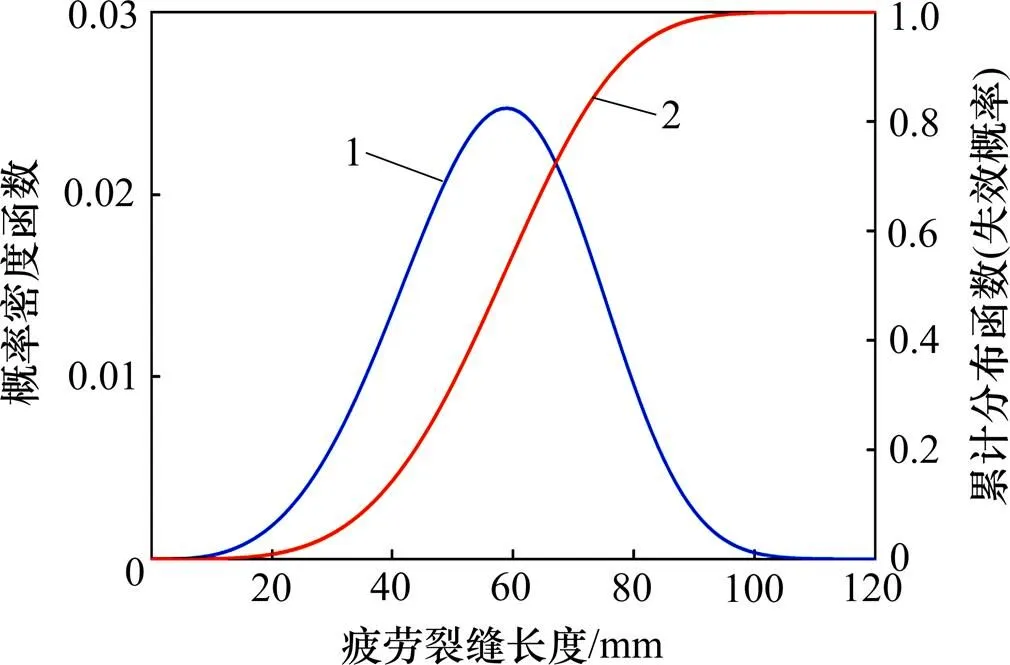
1—概率密度函数(PDF)；2—累计分布函数(CDF)。

以疲劳裂缝长度为症状指标的复合材料结构疲劳可靠度和剩余使用寿命曲线分别见图4和图5。从图4和图5可以看出：结构初始症状可靠度为1，初始设计使用寿命为25 a；随着结构服役时间增加，疲劳裂缝长度逐渐增加，疲劳症状可靠度和剩余使用寿命逐渐减小；当疲劳裂缝长度达到阈值100 mm时，结构症状可靠度降为0，剩余使用寿命降为0 a。

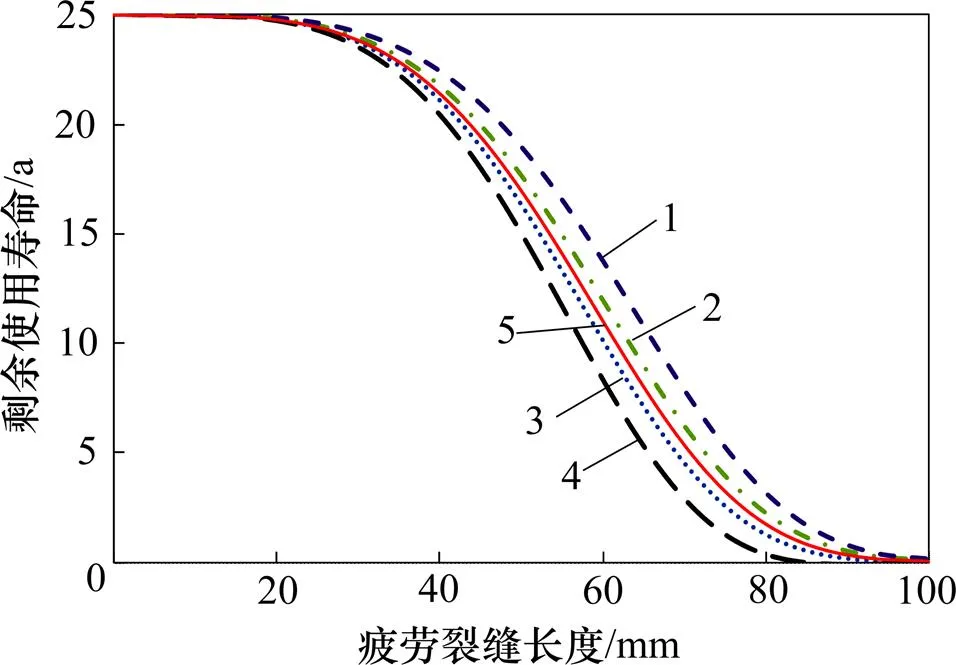
: 1— −0.3；2— −0.1；3—0.1；4—0.3；5—0。

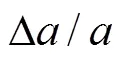
5.2 基于贝叶斯修正的疲劳症状可靠度

通过对风机复合材料叶片进行定期或不定期检测，同时采取一些维护措施，可减小叶片使用过程中的不确定性，从而提高结构的可靠度和剩余使用寿命。本文对检测和/或修复后的风机复合材料叶片，采用贝叶斯方法修正其疲劳症状可靠度。

通过引入似然函数得到基于贝叶斯修正的概率密度函数。在疲劳裂缝长度为40 mm即a=40 mm时进行第1次检测后，采用贝叶斯方法得到的似然函数以及修正前、后的概率密度函数见图6。从图6可以看出：基于疲劳裂缝长度的修正后概率密度函数曲线比修正前初始概率密度函数曲线分布宽度减小，曲线峰值增加。

1—修正前概率密度函数；2—修正后概率密度函数；3—似然函数。

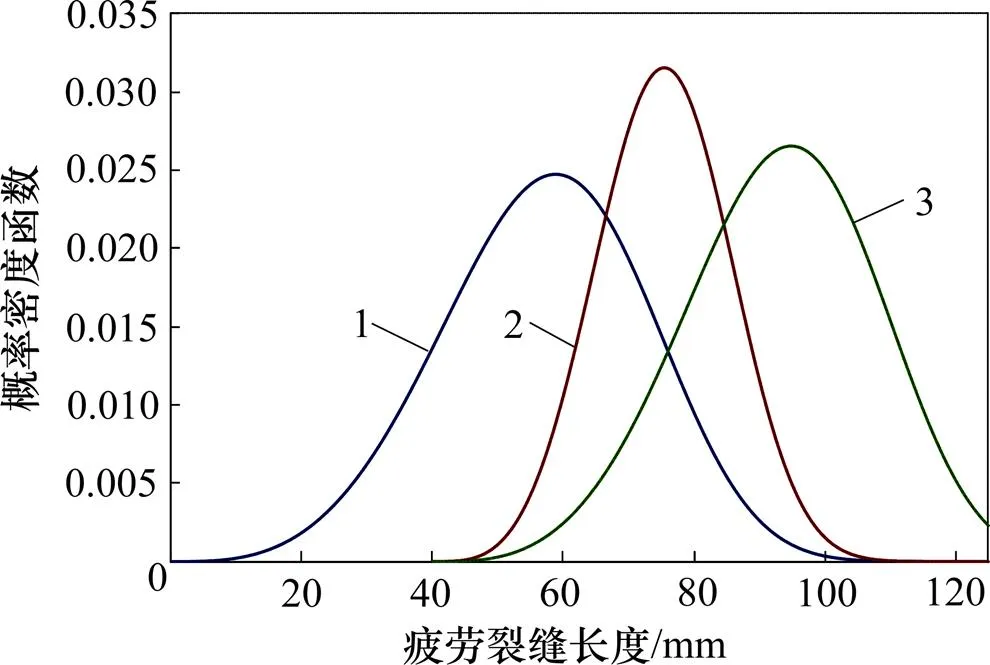
当疲劳裂缝长度为40 mm即a=40 mm时进行第1次检测后，采用贝叶斯方法得到的修正前、后累积分布函数(即结构失效概率)和症状可靠度曲线分别见图7和图8。从图7和图8可以看出：修正后结构失效概率比修正前失效概率明显降低；相应地，修正后结构症状可靠度比修正前结构症状可靠度明显增大。

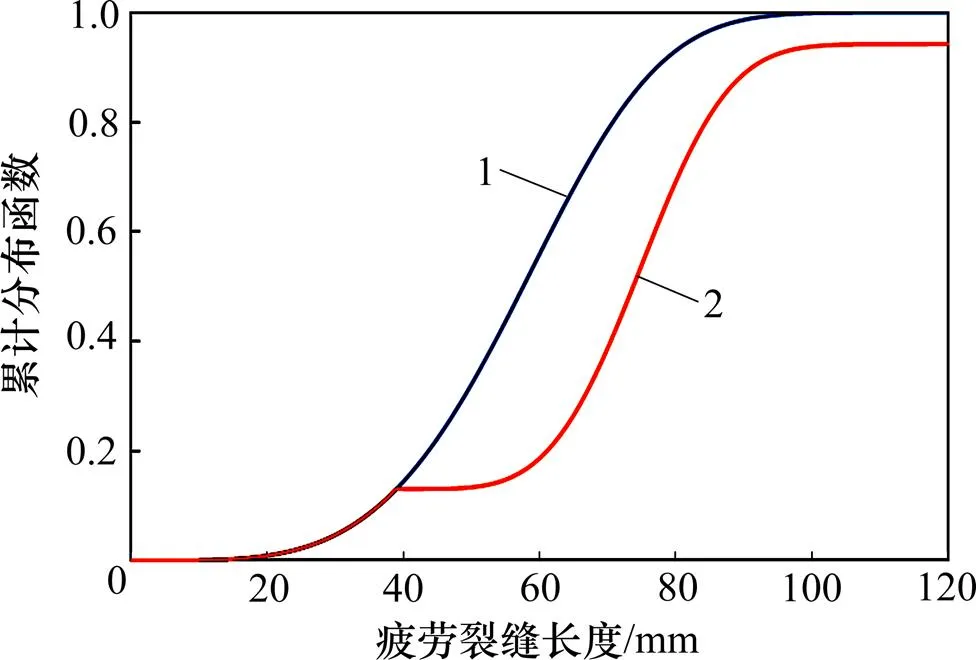
1—修正前累计分布函数(CDF)；2—修正后累计分布函数(CDF)。

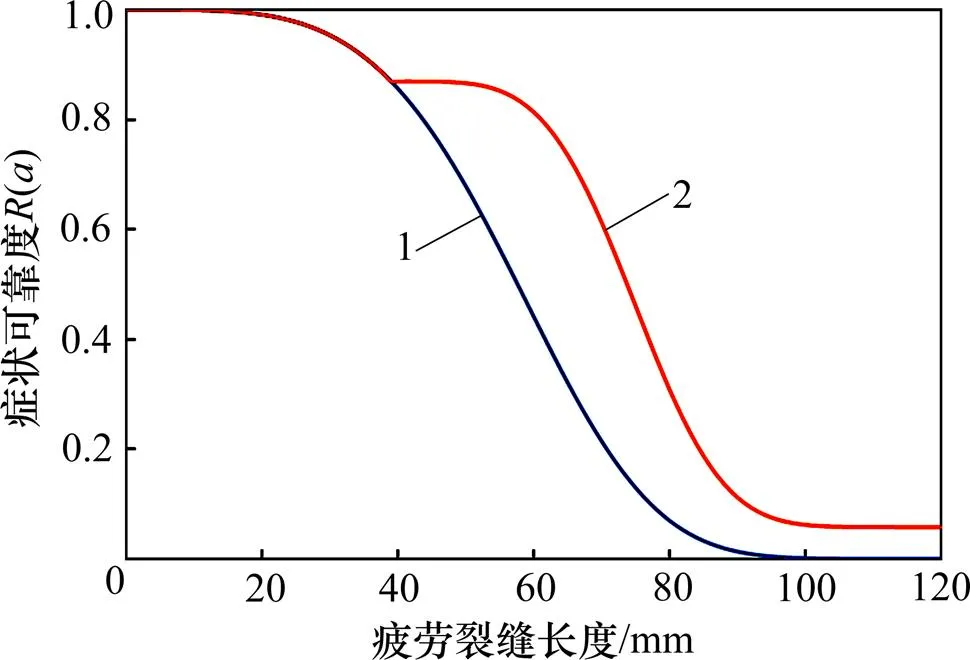
1—修正前症状可靠度R(a)；2—修正后症状可靠度R(a)。

由此表明：对于复合材料结构疲劳损伤，通过检测手段明确其疲劳裂缝长度，可降低疲劳裂缝长度的不确定性，进而有效降低结构的失效风险，增加安全性。

在风机复合材料叶片使用过程中，当疲劳裂缝长度较大时，为保证结构安全和使用，常根据检测获取的实际疲劳裂缝长度，采取裂缝封闭、钻阻裂孔等复合材料疲劳加固修复措施。

假设针对风机复合材料叶片疲劳裂缝采取一定的修复措施后，可使其状态完全恢复到初始状态，即疲劳裂缝长度降为0 mm。第1次检测获取疲劳裂缝长度为40 mm。随着裂缝长度增加，当裂缝长度增加至80 mm即a=80 mm时对风机复合材料叶片进行第1次修复，并且叶片修复到初始完好状态。图9~11所示分别为概率密度函数曲线、累积分布函数(失效概率)曲线和疲劳症状可靠度曲线。

1—未采取检测和修复措施的初始概率密度函数曲线；2—在aa=40 mm时进行检测，在ar=80 mm时进行修复后基于贝叶斯修正的概率密度函数曲线；3—在ar=80 mm时进行修复后基于贝叶斯修正的概率密度函数曲线。

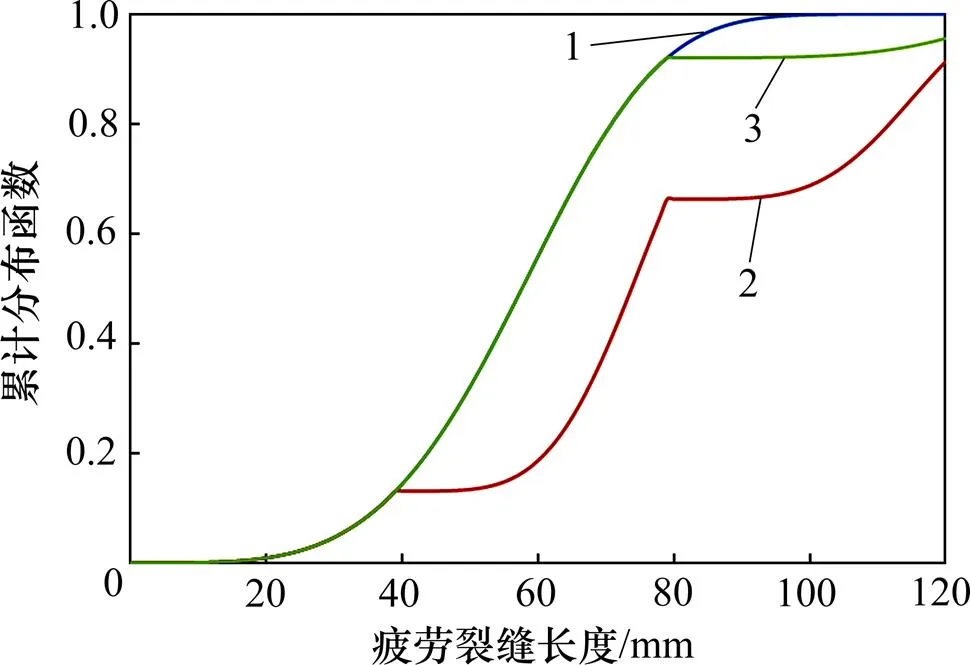
1—未采取检测和修复措施的累积分布函数曲线；2—在aa=40 mm时进行检测，在ar=80 mm时进行修复后，基于贝叶斯修正的累积分布函数曲线；3—在ar=80 mm时进行修复后，基于贝叶斯修正的累积分布函数曲线。

从图9可以看出：采取检测和/或修复措施将显著影响疲劳裂缝长度的概率密度。从图10可以看出：采取检测、修复措施后，结构的失效概率显著减小。从图11可以看出：采取检测、修复措施后，结构的症状可靠度显著增加。对比无检测直接修复和检测后修复2种处理措施可以发现：采取检测后修复处理措施可更有效减低风机复合材料叶片的失效风险水平，增加其症状可靠度水平。由此表明：对于考虑风机复合材料叶片的疲劳问题，在通过检测手段明确疲劳裂缝长度、降低其不确定性的基础上，再采取修复措施，可更加有效降低结构失效风险，增加其安全性。

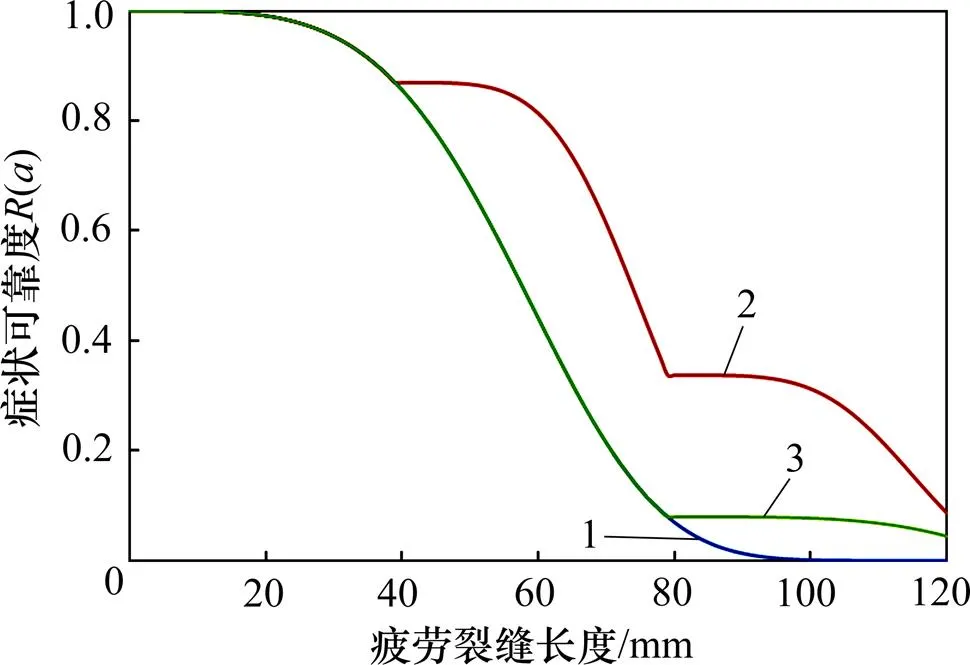
1—未采取检测和修复措施的疲劳症状可靠度曲线；2—在aa=40 mm时进行检测，在ar=80 mm时进行修复后，基于贝叶斯修正的疲劳症状可靠度曲线；3—在ar=80 mm时进行修复后基于贝叶斯修正的疲劳症状可靠度曲线。

5.3 基于全寿命周期维护成本的维护策略优化

为了确定优化的检测、维护策略，以风机复合材料叶片25 a预期全寿命周期中总维护成本最低为优化目标函数，考虑检测、维护措施对叶片疲劳症状可靠度的影响，采用贝叶斯方法予以修正，确定最优的检测和维护时间，并尽可能延长结构的使用寿命。

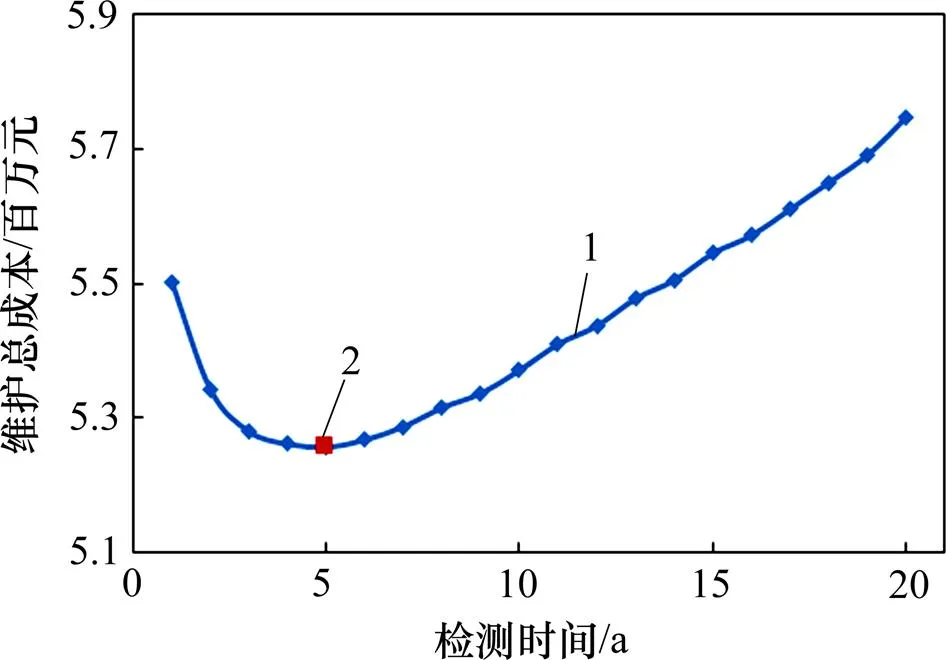
1—维护总费用；2—最低维护总费用。

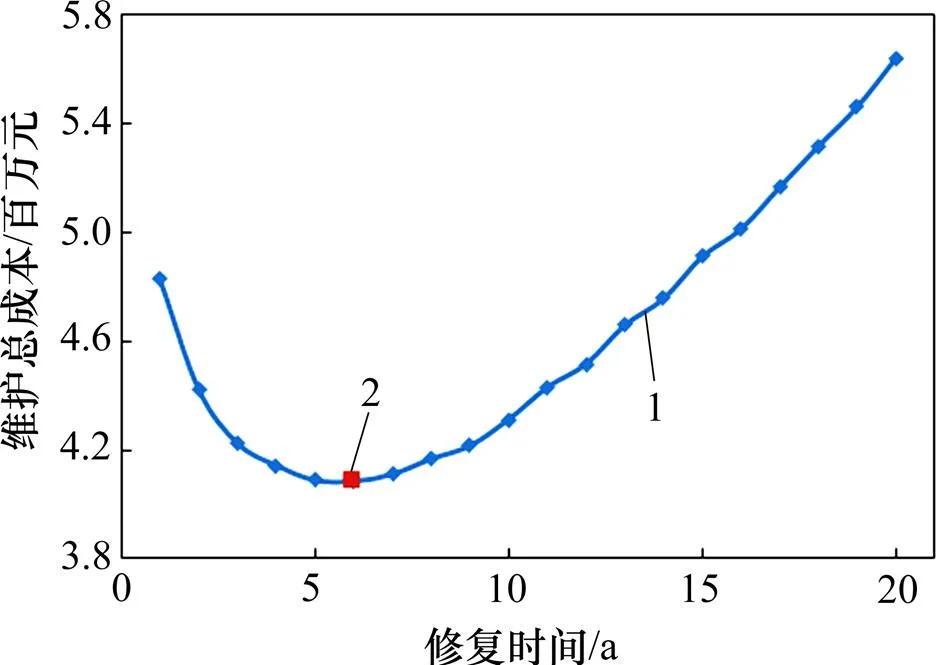
1—维护总费用；2—最低维护总费用。

表1所示为单次检测、单次修复和单次检测+单次修复这3种维护策略的最佳维护时间及维护总成本。从表1可以看出：采用“检测+修复”的综合维护策略所需维护总成本明显比仅进行检测或修复单一维护策略的成本低。由此表明：采用“检测+修复”

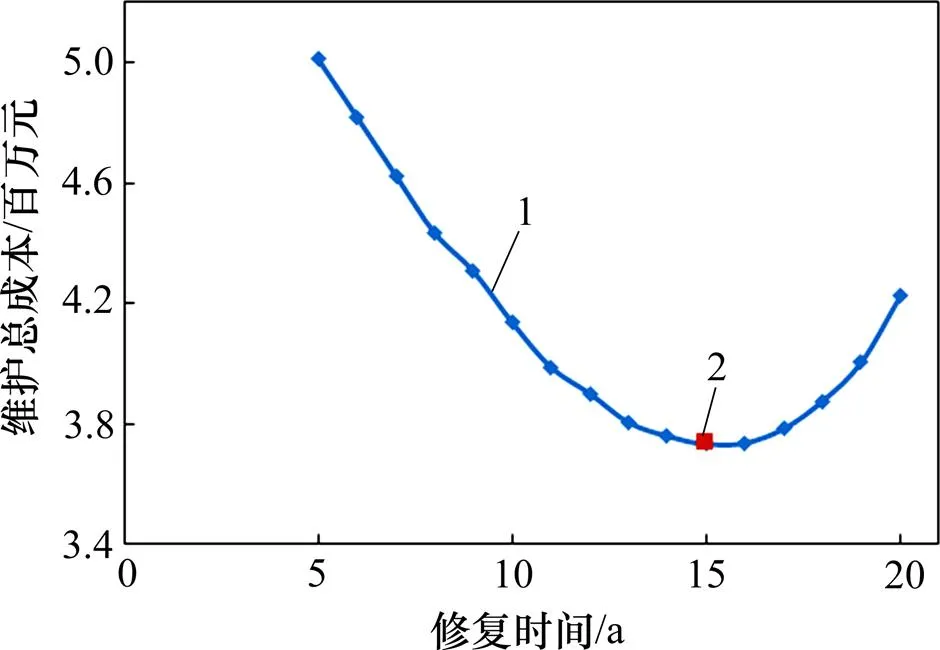
1—维护总费用；2—最低维护总费用。

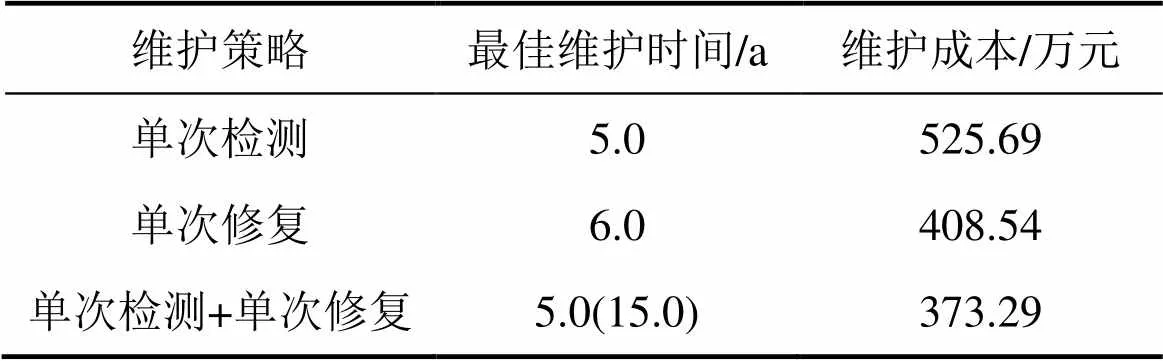
表1 3种不同维护策略的最佳维护时间和总维护成本

注：括号中数据表示修复时间。

综合维护措施比仅采用检测或修复单一维护措施更有效，既降低了总维护成本，又延迟了修复时间。

6 结论

1) 推导了基于刚度退化REIFSNIDER模型的风机复合材料叶片疲劳裂缝长度扩展公式。以疲劳裂缝长度为症状指标，结合WEIBULL症状寿命模型，分析了风机复合材料叶片疲劳症状可靠度，预测了其剩余使用寿命。

2) 检测、修复等维护措施对风机复合材料叶片疲劳失效概率和疲劳症状可靠度有显著影响。在结构寿命周期内，采取检测、修复等维护措施，可有效减低叶片失效风险，增加症状可靠度水平。

3) 采用“检测+修复”综合维护措施比仅采用检测或修复单一维护措施更有效，既降低了总维护成本，又延迟了修复时间。

[1] SORENSEN J D. Framework for risk-based planning of operation and maintenance for offshore wind turbines[J]. Wind Energy, 2009, 12(5): 493−506.

[2] FLORIAN M, SORENSEN J D. Wind Turbine blade life-time assessment model for preventive planning of operation and maintenance[J]. Journal of Marine Science & Engineering, 2015, 3(3): 1027−1040.

[3] YANG J N. Fatigue and residual strength degradation for graphite/epoxy composites under tension-compression cyclic loadings[J]. Journal of Composite Materials, 1978, 12(1): 19−39.

[4] 吴富强, 姚卫星. 纤维增强复合材料剩余强度衰减模型[J]. 南京航空航天大学学报, 2008, 40(4): 517−520. WU Fuqiang, YAO Weixing. Residual strength degradation model of fiber reinforced plastic[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2008, 40(4): 517−520.

[5] WU Fuqiang, YAO Weixing. A fatigue damage model of composite materials[J]. International Journal of Fatigue, 2010, 32(1): 134−138.

[6] 宗俊达, 姚卫星. FRP复合材料剩余刚度退化复合模型[J]. 复合材料学报, 2016, 33(2): 280−286. ZONG Junda, YAO Weixing. Compound model of residual stiffness degradation for FRP composites[J]. Acta Materiae Compositae Sinica, 2016, 33(2): 280−286.

[7] EPAARACHCHI J A, CLAUSEN P D. A new cumulative fatigue damage model for glass fiber reinforced plastic composites under step/discrete loading[J]. Composites Part A, 2005, 36(9): 1236−1245.

[8] MAO H, MAHADEVAN S. Fatigue damage modelling of composite materials[J]. Composite Structures, 2002, 58(4): 405−410.

[9] CEMPEL C, NATKE H G, YAO J T P. Symptom reliability and hazard for systems condition monitoring[J]. Mechanical Systems and Signal Processing, 2000, 14(3): 495−505.

[10] CEMPEL C, TABASZEWSKI M. Multidimensional condition monitoring of machines in non-stationary operation[J]. Mechanical Systems and Signal Processing, 2007, 21(3): 1233−1241.

[11] CERAVOLO R, PESCATORE M, STEFANO A D. Symptom- based reliability and generalized repairing cost in monitored bridges[J]. Reliability Engineering & System Safety, 2009, 94(8): 1331−1339.

[12] CERAVOLO R, STEFANO A D, PESCATORE M. Change in dynamic parameters and safety assessment of civil structures[J]. Mechanics of Time-Dependent Materials, 2008, 12(4): 365−376.

[13] CHEN Huapeng, XIAO Nan. Symptom-based reliability analyses and performance assessment of corroded reinforced concrete structures[J]. Structural Engineering and Mechanics, 2015, 53(6): 1183−1200.

[14] HUANG Tianli, CHEN Huapeng. Symptom-based reliability analysis and remaining service life prediction of deteriorating RC structures[J]. Key Engineering Materials, 2013, 569/570: 151−158.

[15] 肖南, 王海, 陈华鹏, 等. 大气腐蚀下网架结构症状可靠度及寿命预测[J]. 浙江大学学报(工学版)，2013, 47(8): 1373−1378.XIAO Nan, WANG Hai, CHEN Huapeng, et al. Symptom-based reliability and lifetime prediction for latticed structures under atmospheric corrosion[J]. Journal of Zhejiang University (Engineering Science), 2013, 47(8): 1373−1378.

[16] 肖南, 万洁. 考虑应力松弛的张力结构症状可靠度分析[J]. 浙江大学学报(工学版), 2014, 48(7): 1195−1201. XIAO Nan, WAN Jie. Symptom-based reliability analysis for tensile structure considering stress relaxation[J]. Journal of Zhejiang University(Engineering Science), 2014, 48(7): 1195−1201.

[17] REIFSNIDER K L, HENNEKE E G, STINCHCOMB W W, et al. Damage mechanics and NDE of composite laminates[C]// HASHIN Z, HERAKOVICH C T. Mechanics of Composite Materials Recent Advances. Oxford, UK: Elsevier Press Inc, 1983: 399−420.

[18] HUANG Tianli, ZHOU Hao, CHEN Huapeng, et al. Stochastic modelling and optimum inspection and maintenance strategy for fatigue affected steel bridge members[J]. Smart Structures and Systems, 2016, 18(3): 569−584.

[19] CHEN Huapeng, ZHANG Chi, HUANG Tianli. Stochastic modelling fatigue crack evolution and optimum maintenance strategy for composite blades of wind turbines[J]. Structural Engineering and Mechanics, 2017, 63(6): 703−712.

[20] CHEN Huapeng. Monitoring-based reliability analysis of aging concrete structures by Bayesian updating[J]. Journal of Aerospace Engineering, 2017, 30(2): B4015004-1−8.

Symptom-based reliability analysis and optimum maintenance strategy for composite blades of wind turbines

HUANG Tianli1, HE Yanjie1, WANG Ningbo1, ZHANG Chi2, CHEN Huapeng2

(1. School of Civil Engineering, Central South University, Changsha 410075, China; 2. Department of Engineering Science, University of Greenwich, Chatham Maritime, Kent, ME4 4TB, London, UK)

Aiming at the fatigue of composite blades of wind turbines, a formula for calculating the fatigue crack length was deduced based on the REIFSNIDER model of composite laminates. Furthermore, taking the fatigue crack length as the symptom and combining the WEIBULL model, a symptom-based reliability analysis method and a remaining service life prediction method for the composite blades of wind turbines were proposed. The failure probability and the symptom reliability were updated by using Bayesian method due to the influence of inspection and repair. Therefore, taking the life-cycle maintenance cost as the objective function, the procedure for determining the optimum maintenance strategy for the composite blades of wind turbines was proposed. The results show that the level of the fatigue failure probability effectively reduces and the level of the symptom reliability increases by adopting inspections and repairs of composite blades. The combination of inspection and repair measurements is more effective than the single inspection or single repair measurements.

composite wind turbine blades; fatigue; symptom-based reliability; optimum maintenance strategy; Bayesian updating

10.11817/j.issn.1672-7207.2018.07.027

P315.96；TU311.3

A

1672−7207(2018)07−1784−09

2017−10−10；

2017−12−14

国家自然科学基金资助项目(51478472, U1734208, 51508576)；英国皇家工程院牛顿基金资助项目(Reference NRCP/1415/14) (Projects(51478472, U1734208, 51508576) supported by the National Natural Science Foundation of China; Project(Reference NRCP/1415/14) supported the Royal Academy of Engineering-Newton Fund, UK)

王宁波，博士(后)，副教授，从事桥梁结构健康监测研究；E-mail: wangnb@csu.edu.cn

(编辑 陈灿华)