变荷载下考虑结构性的双层地基一维非线性固结分析

崔军，谢康和，夏长青，胡安峰，周禹杉



变荷载下考虑结构性的双层地基一维非线性固结分析

崔军1, 2，谢康和1, 2，夏长青1, 2，胡安峰1, 2，周禹杉1, 2

(1. 浙江大学 滨海和城市岩土工程研究中心，浙江 杭州，310058；2. 浙江大学 软弱土与环境土工教育部重点实验室，浙江 杭州，310058)

考虑变荷载下结构性软土双层地基在固结过程中压缩性和渗透性的非线性变化，基于−lg′两折线压缩模型及−lgv渗透关系，利用半解析方法和成层地基一维固结解析解对结构性软土双层地基一维非线性固结问题进行求解。编制相应的计算程序，通过实例计算，分析变荷载下考虑结构性的双层地基一维非线性固结性状，分别讨论土体结构性、加载速率、结构屈服应力和渗透指数对地基固结性状的影响。研究结果表明：考虑土体结构性影响比未考虑土体结构性的固结速率增大，最终沉降量减小；当最终荷载不变时，随着加载历时的增大，地基固结过程变慢；结构性软土结构屈服应力增大，超静孔压消散加快，土体固结速率增大；双层地基各层渗透指数对超静孔压影响较为复杂，对上下层地基沉降速率影响不同。

结构性软土；双层地基；非线性固结；半解析方法；固结性状

天然沉积土在沉积过程中，普遍存在结构性的特征。很多学者通过大量试验研究后发现，结构性原状土与重塑土在力学特性方面有着明显的区别[1−6]。沈珠江[7−8]从结构性模型观点出发，认为天然土体具有一定结构性，其破坏过程是从原状土到扰动土逐渐转化的过程。土的压缩固结通常呈现非线性的特性，DAVIS等[9]采用土体压缩性和渗透性成正比的假定，推导了均质单层地基一维非线性固结解析解；谢康和等[10−12]基于DAVIS等对土体的假定，给出了变荷载下双层地基一维非线性固结解析解，随后引入−lg′及−lgv(其中：为土体孔隙比；′为土体有效应力；v为渗透系数)关系，利用半解析法，分析变荷载下成层地基一维非线性固结性状，但DAVIS等[9]和谢康和等[10−12]均未考虑土体结构性的影响。在结构性软土固结理论研究方面，也有许多学者进行了大量研究[13−17]，如：王军等[18−19]基于结构性软土压缩试验和工程实践，考虑了土体结构性特征，采用以结构屈服应力为分段点的压缩和渗透两段模型，推导了结构性软土一维固结计算公式，但并未考虑土体在固结过程中相关参数呈非线性连续变化；曹宇春等[20]采用−lg′两段简化模型，推导了天然结构性土体的一维非线性固结方程，并利用Crank-Nicolson有限差分法对方程进行求解，得到相应的固结曲线，但未考虑结构性软土成层性的影响；邓岳保等[21]针对结构性土一维非线性固结问题，通过寻求压缩曲线中的互补条件，构造互补方程组，利用相应算法求解，得到基于互补模型算法的差分解；安然等[22]采用简化的−′和v−′分段模型，将结构性软土一维固结问题转化为上层土体厚度逐渐增加、下层土体厚度不断减小的双层地基一维固结问题，得到了变荷载下结构性软土地基一维固结近似解，但该研究并未实际探讨土体成层性对固结性状的影响，也未考虑土体参数的非线性变化。由于求解困难，以上关于结构性软土固结的研究均未综合考虑土体非线性和成层性的影响。为此，本文作者探讨结构性软土双层地基一维非线性固结问题，假定地基土在固结过程中压缩性和渗透性呈非线性变化，利用半解析方法对地基土在时间和空间上进行离散，并结合成层地基一维固结解析解对本文固结问题进行求解，最后编制相应计算程序，分析变荷载下各因素对结构性软土双层地基一维非线性固结性状的影响。

1 问题描述

图1所示为本文所研究的双层地基模型，该地基厚度为，第层土的厚度、压缩指数、渗透指数、竖向渗透系数和体积压缩系数分别表示为h，ci，ki，vi和vi(=1, 2)。任意深度距地表的距离为。地基表面作用着连续均布变荷载()，荷载情况如图2所示。地基排水条件分为2种：单面排水(仅地基表面透水)和双面排水(地基表面和底面均透水)。

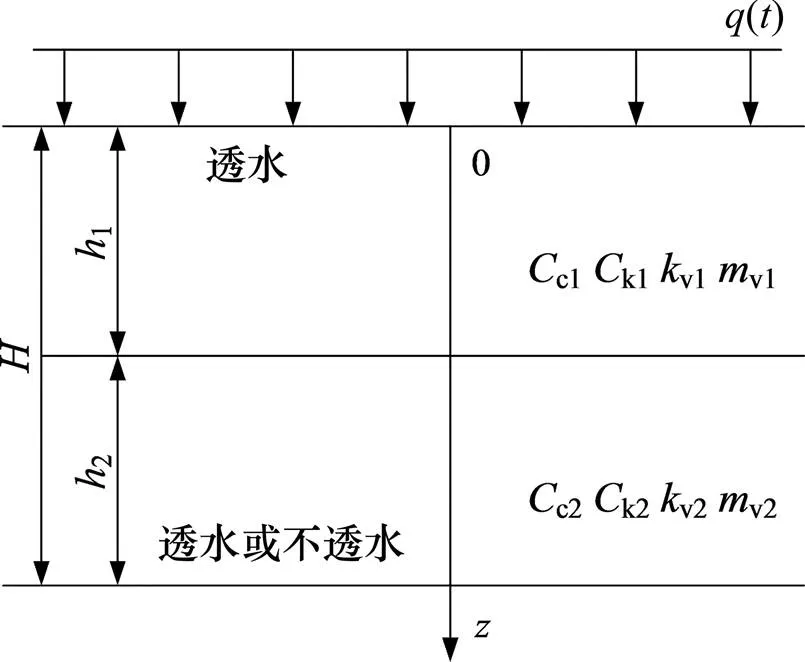
图1 结构性软土双层地基模型

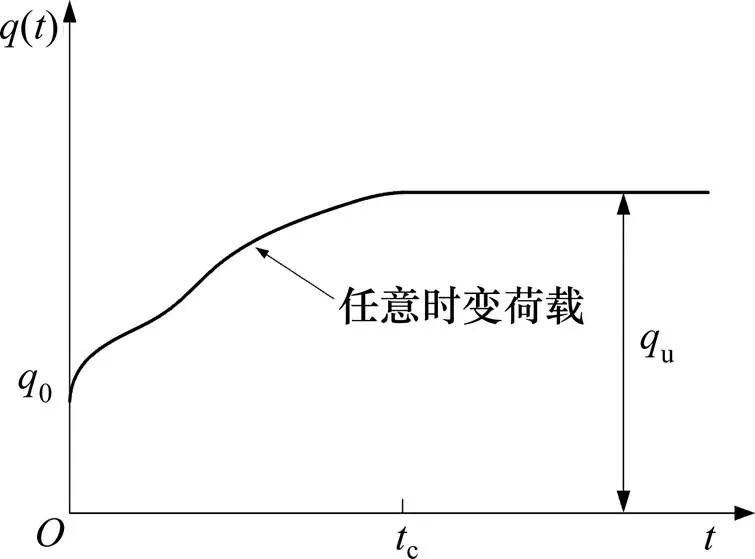
图2 荷载与时间的关系

大量天然土体试验研究表明土体在固结过程中渗透性的变化规律为

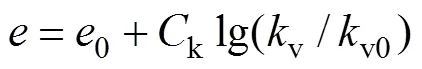
式中：0为土体初始孔隙比；k为渗透指数；v0为初始渗透系数。

本文采用−lg′两折线压缩模型[3]，如图3所示，则压缩性方程为

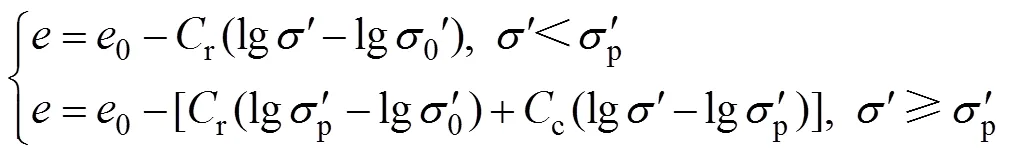
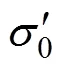
取土体结构屈服应力计算公式为[23]：

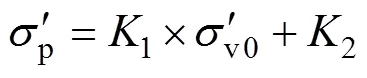
式中：为上覆应力；K1和K2为待定系数，分别考虑次压缩作用和化学胶结作用对土体结构性的影响，对同一层软土进行压缩试验，测定不同深度土样的结构屈服应力和上覆应力，利用所拟合直线的斜率和截距可确定K1和K2[23]。

2 问题求解与验证

2.1 解答

在结构性软土一维固结问题研究中，需要确定土体屈服前阶段和屈服后阶段的分界面深度，随着固结不断发展，分界面深度c随时间不断变化，难以得到固结方程的解析解，故本文在已有研究基础上，采用半解析法，对图1所示的双层地基在空间和时间上进行离散，将结构性软土非线性固结问题转化为每一时间段每一薄层土的线性固结问题，利用成层地基线性固结解析解计算得到该时间段下每一薄层的超静孔压，通过计算有效应力，并与结构屈服应力比较判断土体屈服前阶段和屈服后阶段分界面深度c；随固结过程发展，逐步计算出各土层参数。

图4所示为双层地基的空间离散图。将厚度为的双层地基均匀划分为个薄层，每一薄层从上至下标记为(=1, 2, …,)，则其厚度h均为/，令坐标原点位于地表，第层上下表面坐标分别为z−1和z。同时，将固结时间进行离散，划分为足够小的若干时间段，用来表示其中任一时间段，第个时间段起始时刻、终止时刻分别为t−1和t，=1, 2, …，时间步长为Δt=t–t−1，初始时刻0=0。随着时间的离散，对于荷载也进行相应的离散化，由于时间段足够小，在任一微小时段内，荷载被认为是瞬时施加荷载，将变荷载固结问题转化为常荷载固结问题。若所加荷载足够大，则双层土体由屈服前阶段逐层发展为屈服后阶段，分界面深度c不断增大至。

空间和时间分别离散后，由于时间划分足够小，双层地基每一薄层在时段内的渗透性和压缩性变化微小，可近似用t−1时刻的土体参数表示各薄层在时段内的平均值，第薄层在时段内的体积压缩系数vij、渗透系数vij和固结系数vij平均值可表示为：

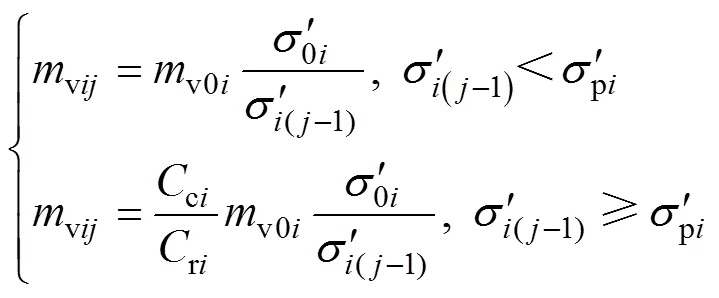
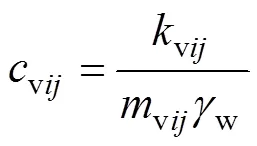
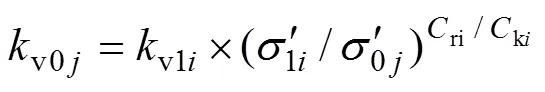
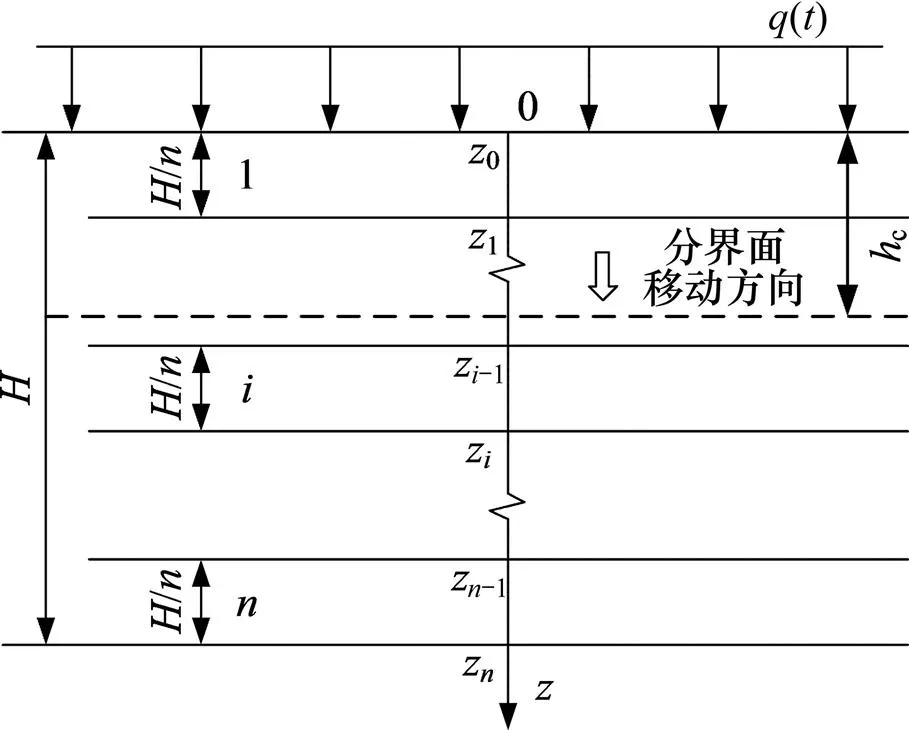
图4 双层地基的空间离散

此时，双层地基中第薄层在任意微小时段内的固结控制方程为

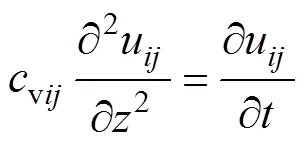
其相应的求解条件如下。

1) 边界条件：

2) 初始条件：

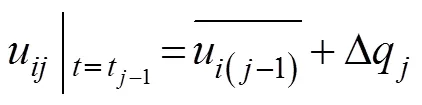
3) 层间连续条件：

(=1, 2, 3, …,−1) (10)

基于上述固结控制方程和求解条件，谢康和等[24]给出了详尽的解答：

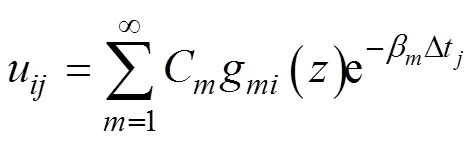
C和g的表达式参见文献[24]。

则任一薄层在时段内按应力定义的固结度为

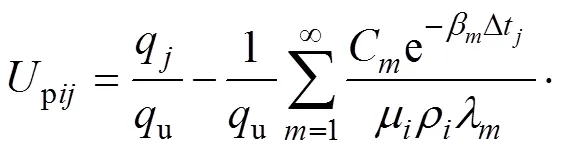
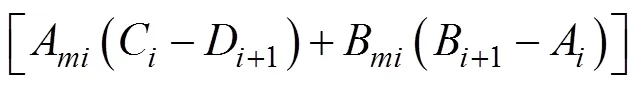
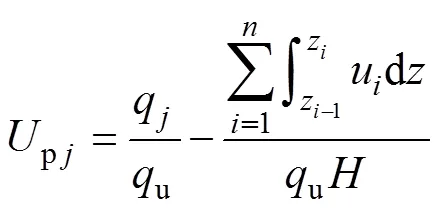
双层地基任一薄层在时段内的沉降为

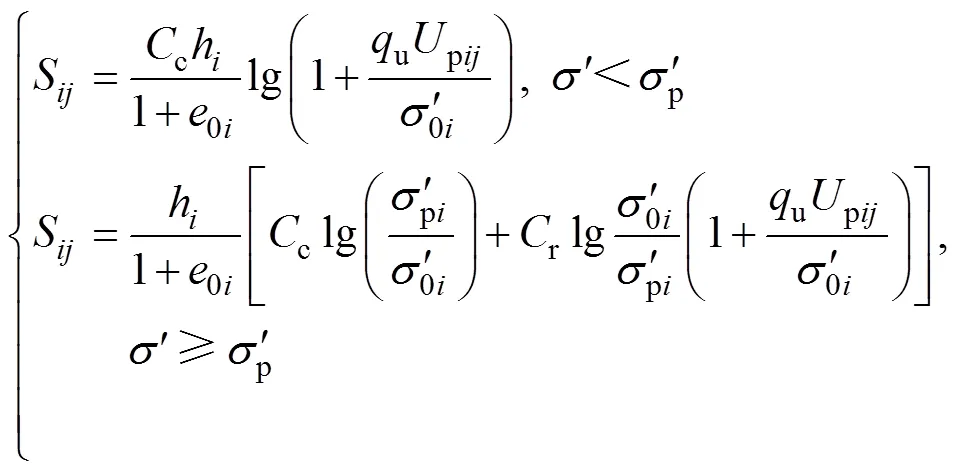
在分别计算出双层地基各薄层沉降后，在t时刻地表沉降为

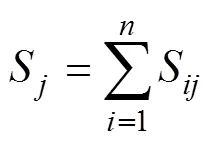
双层地基最终沉降量为

则按沉降定义的双层地基总平均固结度为

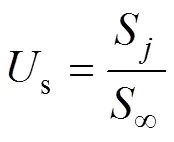
2.2 验证

基于上述对双层地基一维固结问题的半解析方法，采用Fortran语言编制了相应的计算程序。当r=c时，两折线压缩模型可退化为重塑土压缩模型，为检验本文计算程序的正确性，令第1层土r1=c1=0.328，第2层土r2=c2=0.405，与不考虑土体结构性的双层地基一维非线性固结半解析解进行对比，其中荷载线性施加，0=0，u=250 kPa，时间因子vc=0.083 2(加载时间c=365.12 d)，边界条件为双面排水条件，且其余计算参数均相同，分别计算s和p随lgv的变化情况，对比结果如图5所示。由图5可见：两者计算结果较吻合，由此可判断，本文所采用的半解析方法和计算程序是可靠的。

大白兔“诞生”于1959年，美加净“诞生”于1962年，在那个年代，大白兔奶糖和美加净护肤品风靡一时，受到消费者的喜爱。大白兔成为建国十周年的献礼产品，产品经销全世界40多个国家和地区，成为国际市场上经久不衰的大众宠儿。美加净创造了很多中国化妆历史上的“第一”，第一支护发定型摩丝、第一款护手产品——美加净护手霜，上海家化还推出了美加净青苹果香波，这是国内首个“二合一”（洗发+护发）香波洗发水。

图5 不考虑结构性的半解析与本文解对比验证

3 实例分析

某双层天然地基土体完全饱和，外荷载线性施加，0=0，u=250 kPa，时间因子vc=0.083 2(加载时间c=365.12 d)。表1所示为双层地基各土层计算参数，本文以此双层地基为例，分析线性荷载下各因素对结构性软土双层地基一维非线性固结性状的影响。

3.1 土体结构性的影响

图6所示为考虑土体结构性对固结度和沉降的影响，边界条件为双面排水条件。图6(a)所示为考虑土体结构性与否2种情况下，固结度随变化的曲线，由图6(a)可见：由于土体结构性影响，土体固结速率增大，在任一时刻，考虑土体结构性情况下按应力定义的平均固结度p均更大，在固结过程中，考虑结构性与否对p影响更为显著。由图6(b)可见：考虑土体结构性时，沉降量增加缓慢，最终沉降量减小。

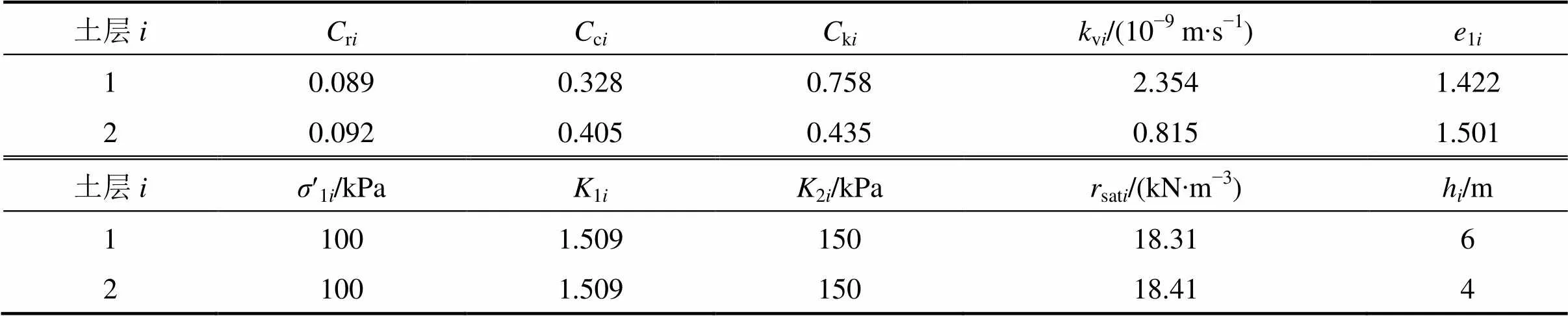
表1 双层地基计算参数

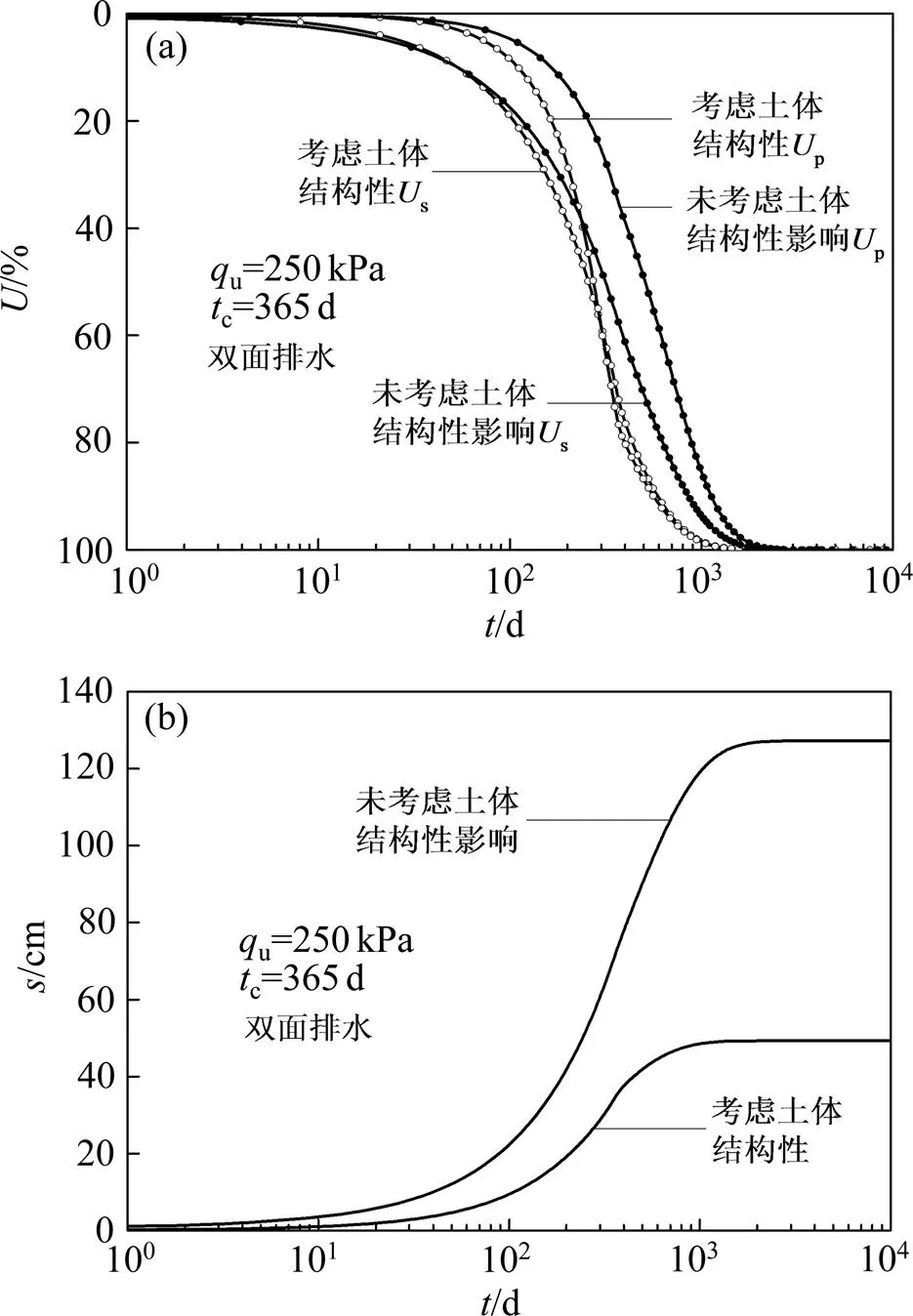
(a) 固结度U；(b) 沉降s

3.2 加载速率的影响

为探究不同加载速率下固结度和沉降量随时间变化的关系。取荷载为线性施加荷载，0=0，u=250 kPa，加载历时c为0，182.56，365.12和547.68 d，边界条件为双面排水条件。

图7(a)所示为不同加载速率下固结度随lgv的变化规律。由图7(a)可见：加载历时c越大，即加载速率越小，固结度增加越慢。曲线各点处对应的斜率为此时刻固结发展速率，在固结初期，瞬时荷载下固结速率大于线性加载的情况，并且随着时间增长，固结发展速率呈现先增大后减小的规律；线性加载情况在初期土体固结发展缓慢，随时间增长，固结发展速率呈现迅速增大后迅速减小的规律；在整体固结过程中，瞬时荷载下最大固结速率比线性加载情况下的小。

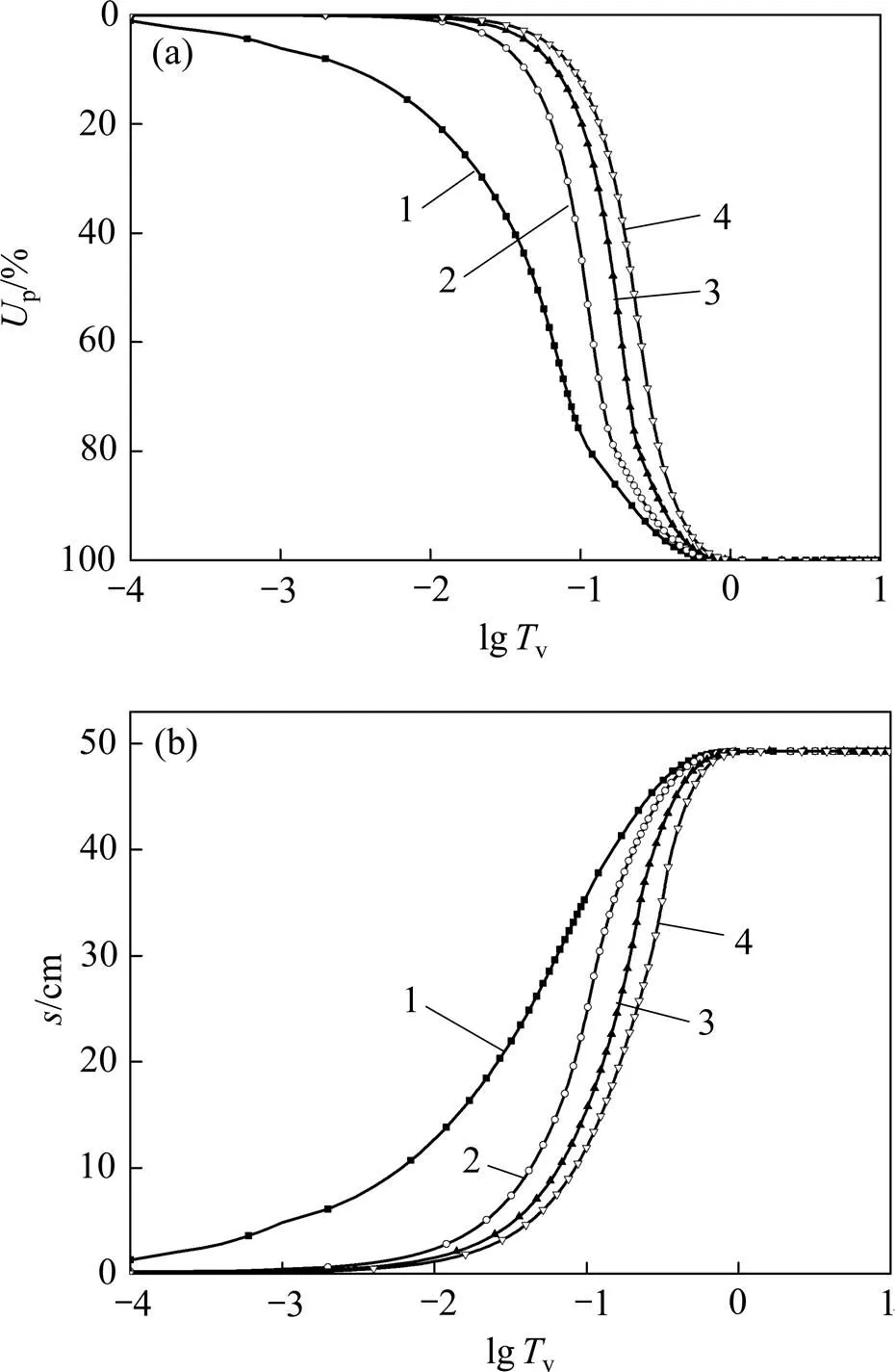
(a) 固结度Up；(b) 沉降s

图7(b)所示为不同加载历时下沉降随lgv的变化规律。由图7(b)可见：随加载历时c增大，沉降发展速率减小；曲线各点处对应的斜率为此时刻的沉降发展速率，线性加载情况下最大沉降发展速率大于瞬时加载的，在本文对比组中，c=182.56 d对应的沉降随时间发展曲线斜率最大；在u相同、不同加载速率下，土层最终沉降量相同，并且达到最终沉降的时间接近。

3.3 结构屈服应力的影响

对于结构性软土，当土层总应力大于其结构屈服应力时，土体发生结构破坏，其渗透性和压缩性发生显著变化，土体超静孔压消散速率与结构屈服应力密切相关。

图8所示为不同结构屈服应力下超静孔压等时曲线。在其他参数不变的情况下，改变结构屈服应力参数2i(=1,2)，令其分别为100，150和200 kPa，荷载线性施加，边界条件为双面排水条件。由图8可知：在固结过程初期，=180.99 d时，由于土体未发生显著结构破坏，超静孔压消散速率基本相同，图中不同2i下超静孔压等时曲线较为接近；随时间增长，当为363.6 d和565.59 d时，参数2i越大即土体结构屈服应力越大，超静孔压越小，土体固结过程发展越快；参数2i=100 kPa时，=363.6 d对应的超静孔压比=180.99 d时大，是因为结构屈服应力参数较小，在土体发生屈服后，孔隙比减小，渗透系数减小，而此时外荷载仍在增大，超静孔压不能及时消散，导致超静孔压增大。

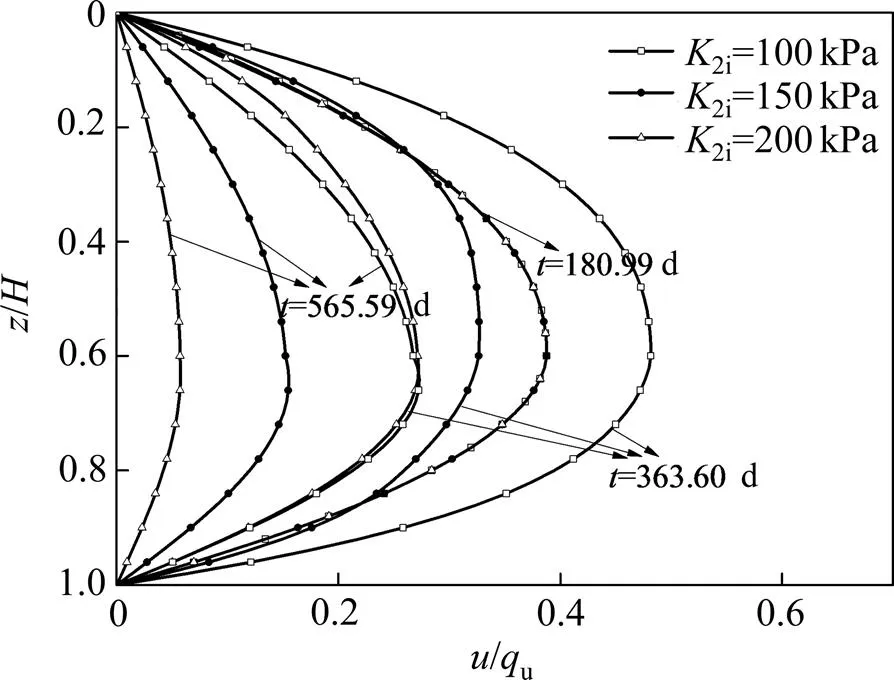
图8 不同结构屈服应力下超静孔压等时曲线

3.4 渗透指数的影响

图9~12所示为双层地基各层渗透指数ki对土层沉降和应力发展的影响。0=0，u为250 kPa，加载历时c= 183 d，排水条件分别为单面排水和双面排水。

为探究第1层土渗透指数k1变化的影响，在表1所示数据的基础上，令k1分别为0.379，0.758和1.137，k2为0.435。图9所示为不同k1下土层沉降随时间变化的关系。由图9可见：在单面排水条件下，随着第1层土渗透指数的增大，沉降速率增大；在双面排水条件下，随着第1层土渗透指数的增大，沉降速率总体上是增大的，但影响并不明显；双面排水条件下的沉降速率比单面排水条件的大，达到最终沉降所需时间短。

图10所示为不同k1下超静孔压沿深度方向变化关系。由图10(a)可见：单面排水条件下，在固结初始阶段，当=164 d时，第1层土渗透指数k1越大，第1层土上部超静孔压减小，应力消散速率增大，但第1层土下部和第2层土超静孔压增大，应力消散速率减小；当=329 d和497 d时，土层中随着k1增大，超静孔压减小，超静孔压消散速率增大；随土中k1增大，超静孔压消散速率总体呈现增大的趋势。由图10(b)可见：在双面排水条件下，在固结过程初期，第1层土渗透指数的变化对超静孔压消散速率影响不明显，随着固结过程的发展，在为329 d和497 d时，第1层土渗透指数k1越大，超静孔压越小，孔压消散 越快。

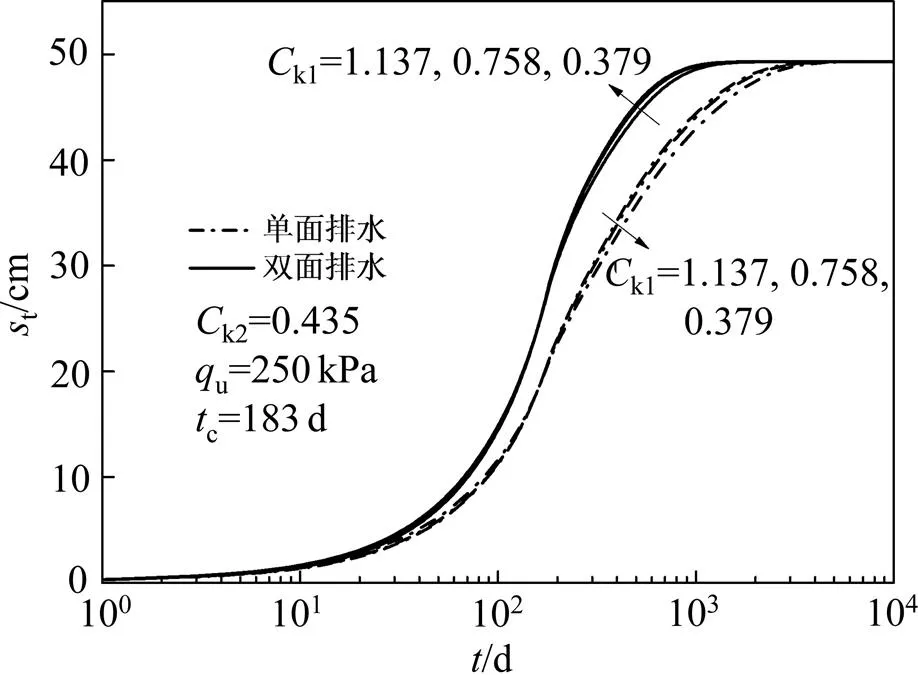
图9 第1层土渗透指数对沉降影响

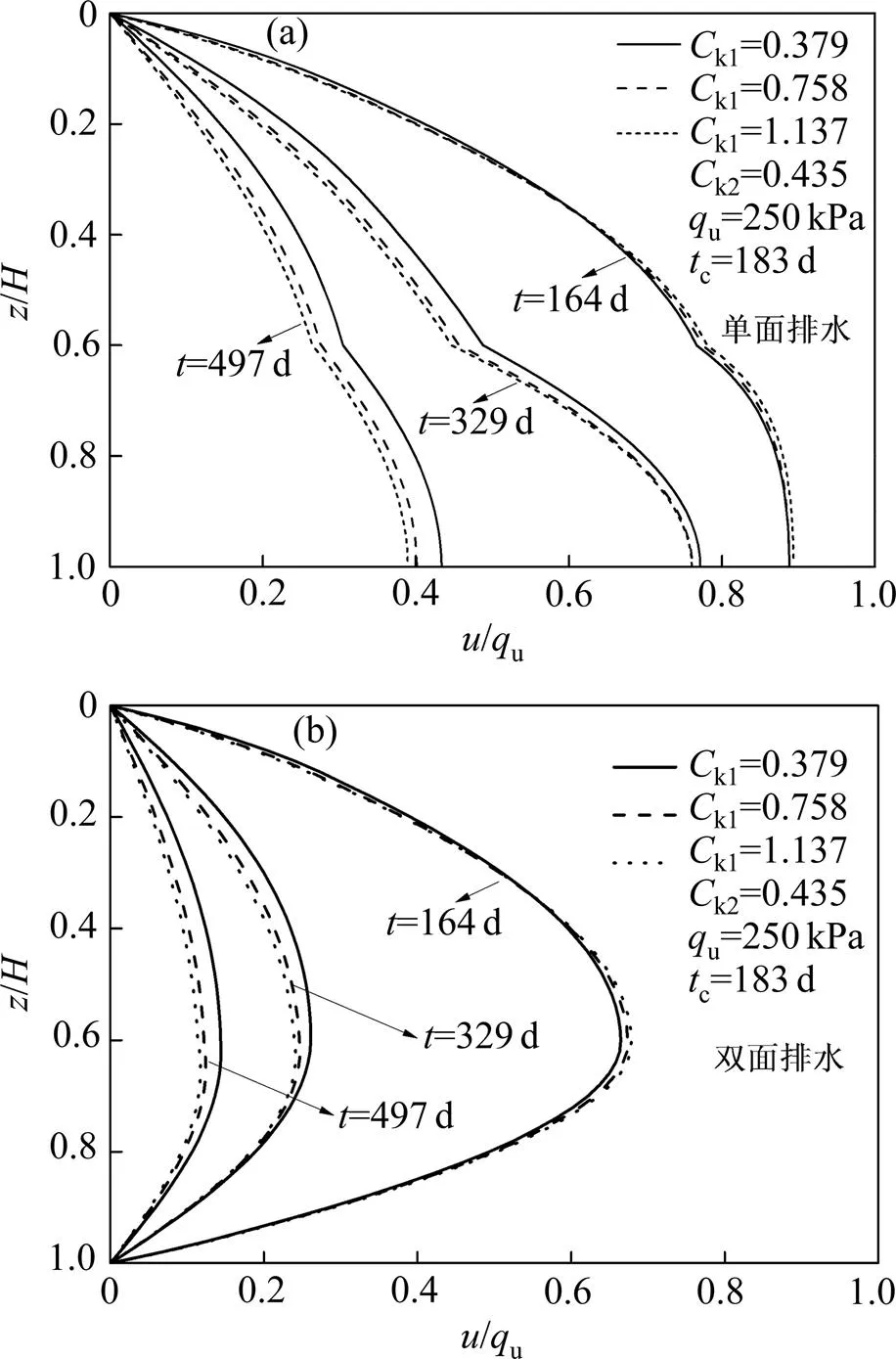
(a) 单面排水条件；(b) 双面排水条件

为探究第2层土渗透指数k2变化的影响，在表1所示数据的基础上，令k1为0.435，k2分别为0.379，0.758和1.137。图11所示为不同k2下土层沉降随时间变化的关系。由图11可见：在单面排水和双面排水2种情况下，不同k2对土层沉降没有显著影响；在沉降发展接近完全时，随k2增大，沉降速率略微增加，最终沉降量相同；双面排水条件下达到最终沉降所需时间更短。

图12所示为不同k2下超静孔压沿深度方向变化关系。由图12(a)可见：在单面排水条件下，随着k2的增大，第1层土中超静孔压增大，但在整体固结过程中影响并不显著，对于第2层土，渗透指数k2对超静孔压的影响较复杂，在固结初始阶段，随k2增大，超静孔压值增大，超静孔压消散速率减小，但随着固结发展，k2增大，超静孔压不断减小。由图12(b)可见：双面排水条件下，在固结整体过程中，第2层土渗透指数k2越大，超静孔压越小，孔压消散速率越大。

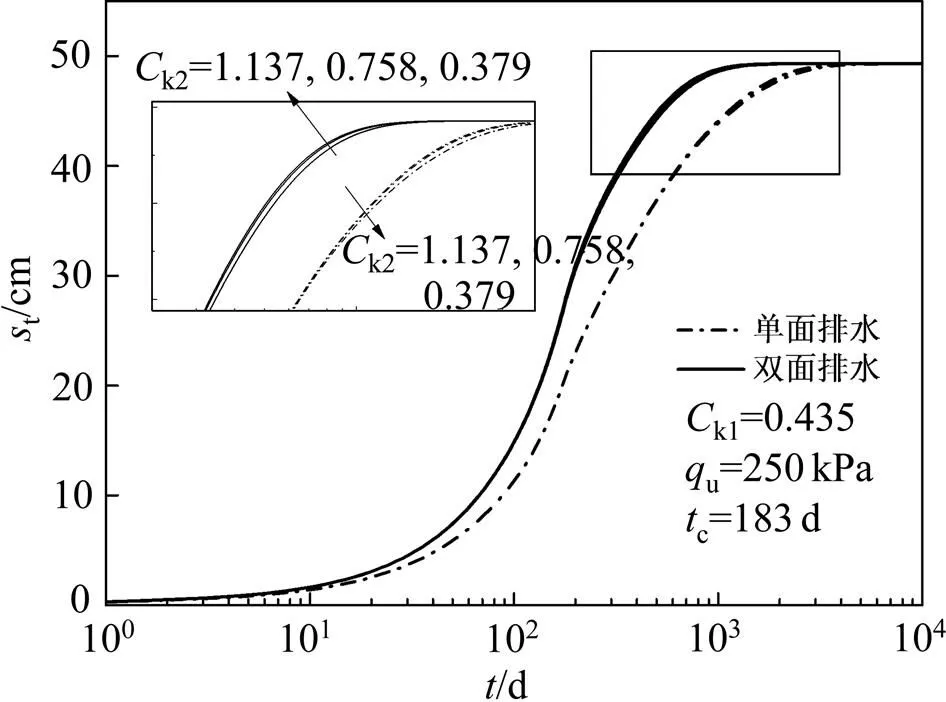
图11 第2层土渗透指数对沉降影响

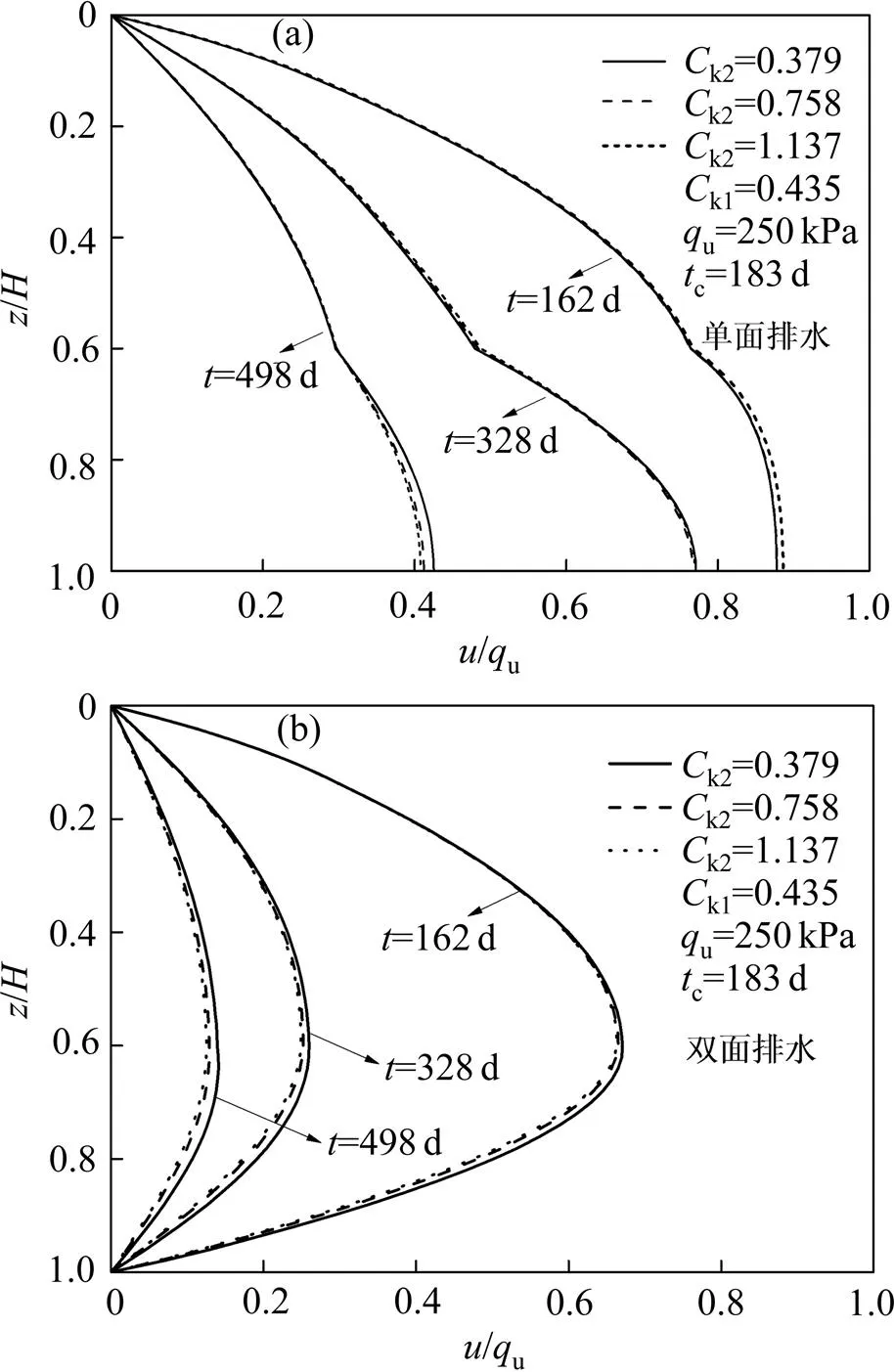
(a) 单面排水条件；(b) 双面排水条件

4 结论

1) 考虑土体结构性影响比未考虑土体结构性的固结速率增大，最终沉降量减小，并且考虑土体结构性与否对p影响更显著。

2) 保持最终荷载u不变，随着加载历时c的增大即加载速率减小，固结度p增加越慢，沉降量发展越慢；在整体固结过程中，线性加载情况下最大固结发展速率和最大沉降发展速率均比瞬时加载情况 的大。

3) 土体结构屈服应力对固结速率有较大的影响，结构屈服应力越大，则超静孔压越小，超静孔压消散速率越快，土体固结速率越快。

4) 双层地基各层渗透指数ki对固结速率有一定影响，随着第1层土渗透指数k1增大，单面排水条件下沉降速率增大，超静孔压消散速率总体呈现增大的趋势，而双面排水条件下对沉降速率影响不明显，超静孔压消散加快；随着第2层土渗透指数k2增大，对沉降影响不显著，单面排水条件下对上下两层土超静孔压的影响较为复杂，双面排水条件下超静孔压消散加快。

[1] BURLAND J B. On the compressibility and shear strength of natural clays[J]. Geotechnique, 1990, 40(3): 329−378.

[2] HONG Z S, LIU H L, TAKEHITO N. Remolded Undrained Strength of Soils[J]. China Ocean Engineering, 2003, 17(1): 133−142.

[3] 王立忠, 丁利, 陈云敏,等. 结构性软土压缩特性研究[J]. 土木工程学报, 2004, 37(4): 46−53.WANG Lizhong, DING Li, CHEN Yunmin, et al. Study on compressibility of structured soft soil[J]. China Civil Engineering Journal, 2004, 37(4): 46−53.

[4] 洪振舜, 刘松玉, 于小军. 关于结构土屈服破坏的探讨[J]. 岩土力学, 2004, 25(5): 684−687. HONG Zhenshun, LIU Songyu, YU Xiaojun. On destructuration of structured soils[J]. Rock and Soil Mechanics, 2004, 25(5): 684−687.

[5] 洪振舜, 立石义孝, 邓永锋. 强结构性天然沉积土的强度变形特性[J]. 岩土力学, 2004, 25(8): 1201−1204. HONG Zhenshun, TATEISHI Yoshitaka, DENG Yongfeng. Mechanical behavior of a strongly-structured natural sedimentary soil[J]. Rock and Soil Mechanics, 2004, 25(8): 1201−1204.

[6] 柳艳华, 谢永利. 基于结构性及各向异性的软黏土变形性状试验[J]. 地球科学与环境学报, 2014, 36(2): 135−142.

LIU Yanhua, XIE Yongli. Test on deformation character of soft clay based on structure and anisotropy[J]. Journal of Earth Sciences and Environment, 2014, 36(2): 135−142.

[7] 沈珠江. 原状取土还是原位测试[J]. 岩土工程学报, 1996, 18(5): 90−91. SHEN Zhujiang. Undisturbed soil sampling or in situ testing[J] Chinese Journal of Geotechnical Engineering, 1996, 18(5): 90−91.

[8] 沈珠江. 土体结构性的数学模型: 21世纪土力学的核心问题[J]. 岩土工程学报, 1996, 18(1): 95−97. SHEN Zhujiang. The mathematics model of soil structure: the key problem of soil mechanics for the 21 century[J]. Chinese Journal of Geotechnical Engineering, 1996, 18(1): 95−97.

[9] DAVIS E H, RAYMOND G P. A non-linear theory of consolidation[J]. Geotechnique, 1965, 15(2): 161−173.

[10] 谢康和, 郑辉, 李冰河, 等. 变荷载下成层地基一维非线性固结分析[J]. 浙江大学学报(工学版), 2003, 37(4): 426−431. XIE Kanghe, ZHEN Hui, LI Binghe, et al. Analysis of dimensional nonlinear consolidation of layered soils under time-dependent loading[J]. Journal of Zhejiang University (Engineering Science), 2003, 37(4): 426−431.

[11] XIE K H, XIE X Y, JIANG W. A study on one-dimensional nonlinear consolidation of double-layered soil[J]. Computers and Geotechnics, 2002, 29(2): 151−168.

[12] XIE K H, LI B H, LI Q L. A nonlinear theory of consolidation under time-dependent loading[C]// SHEN Z J. Proceedings of the 2nd International Conference on Soft Soil Engineering. Vol.1. Nanjing: Hohai University Press, 1996: 193−198.

[13] 吴浩, 谢康和, 黄大中. 第二类越流系统中结构性弱透水土层一维固结解析解[J]. 岩土工程学报, 2014, 36(9): 1688−1695. WU Hao, XIE Kanghe, HUANG Dazhong. Analytical solution for one-dimensional consolidation of structured aquitard soils in second kind of leakage system[J]. Chinese Journal of Geotechnical Engineering, 2014, 36(9): 1688−1695.

[14] XIE K H, XIA C Q, AN R, et al. A study on the one-dimensional consolidation of double-layered structured soils[J]. Computers and Geotechnics, 2016, 73: 189−198.

[15] XIE K H, XIA C Q, AN R, et al. A study on one-dimensional consolidation of layered structured soils[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2016, 40(7): 1081−1098.

[16] HU A F, XIA C Q, WU H, et al. A study on one-dimensional consolidation of layered structured aquitard soils in a leakage system[J]. Marine Georesources & Geotechnology, 2017, 35(3): 318−329.

[17] HU A F, XIA C Q, CUI J, et al. Nonlinear consolidation of natural structured clays under time-dependent loading[J]. International Journal of Geomechanics, 2018, 18(2): 04017140.

[18] 王军, 陈云敏. 均质结构性软土地基的一维固结解析解[J]. 水利学报, 2003, 34(3): 19−24. WANG Jun, CHEN Yunmin. Analytical solution to 1-D consolidation of homogeneous structured soft foundation[J]. Journal of Hydraulic Engineering, 2003, 34(3): 19−24.

[19] CHEN Y M, TANG X W, WANG J. An analytical solution of one-dimensional consolidation for soft sensitive soil ground[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2004, 28(9): 919−930.

[20] 曹宇春, 陈云敏, 黄茂松. 任意施工荷载作用下天然结构性软粘土的一维非线性固结分析[J]. 岩土工程学报, 2006, 28(5): 569−574. CAO Yuchun, CHEN Yunmin, HUANG Maosong. One- dimensional nonlinear consolidation analysis of structured natural soft clay subjected to arbitrarily time-dependent construction loading[J]. Chinese Journal of Geotechnical Engineering, 2006, 28(5): 569−574.

[21] 邓岳保, 谢康和. 基于互补算法的结构性软基一维非线性固结解[J]. 工程力学, 2012, 29(3): 163−169. DENG Yuebao, XIE Kanghe. Solution for one dimensional non-linear consolidation of structured soil with complementary algorithm[J]. Engineering Mechanics, 2012, 29(3): 163−169.

[22] 安然, 谢康和, 邓岳保, 等. 变荷载下结构性土一维固结近似解[J]. 岩土力学, 2012, 33(10): 3194−3200. AN Ran, XIE Kanghe, DENG Yuebao, et al. Approximate solution for one-dimensional consolidation of structured soils under time-dependent loading[J]. Rock and Soil Mechanics, 2012, 33(10): 3194−3200.

[23] 王立忠, 李玲玲. 结构性土体的施工扰动及其对沉降的影响[J]. 岩土工程学报, 2007, 29(5): 697−704. WANG Lizhong, LI Lingling. Field disturbance of structured clay and its effect on settlements of soil foundation[J]. Chinese Journal of Geotechnical Engineering, 2007, 29(5): 697−704.

[24] 谢康和, 潘秋元. 变荷载下任意层地基一维固结理论[J]. 岩土工程学报, 1995, 17(5): 80−85.XIE Kanghe, PAN Qiuyuan. One dimensional consolidation theory of arbitrary layers under time-dependent loading[J]. Chinese Journal of Geotechnical Engineering, 1995, 17(5): 80−85.

One-dimensional nonlinear consolidation analysis of double layered structured soils under time-dependent loading

CUI Jun1, 2, XIE Kanghe1, 2, XIA Changqing1, 2, HU Anfeng1, 2, ZHOU Yushan1, 2

(1Research Center of Coastal and Urban Geotechnical Engineering, Zhejiang University, Hangzhou 310058, China;2. MOE Key Laboratory of Soft Soils and Geoenvironmental Engineering, Zhejiang University, Hangzhou 310058, China)

Based upon the nonlinear variation of compressibility and permeability in the process of consolidation, and based on−lg′ two-stage compression model and−lgvrelationships, one-dimensional nonlinear consolidation problem of double layered structured soft soils was solved by using semi-analytical method and analytical solutions for one-dimensional nonlinear consolidation. A corresponding computer program was developed, and then consolidation behavior is discussed by practical calculation examples. The results show that the rate of consolidation with considering soil structure effect becomes faster than that without considering soil structure effect. If the ultimate load remains unchanged, the greater the loading time, the more slowly the total process of consolidation. The greater the yield stress of structured soft soil, the smaller the excess pore water pressure, and the faster the development of soil consolidation. In the process of consolidation, the influence of permeability index for double layered foundation is more complicated, and is different for the consolidation rate in the upper and the lower layers.

structured soft soils; double-layered soils; nonlinear consolidation; semi-analytical method; consolidation behavior

10.11817/j.issn.1672-7207.2018.07.018

TU43

A

1672−7207(2018)07−1710−08

2017−07−02；

2017−09−19

国家自然科学基金资助项目(51778572，51278453)；国家教育部博士点基金资助项目(20120101110029) (Projects(51778572, 51278453) supported by the National Natural Science Foundation of China; Project(20120101110029) supported by the Ph.D. Programs Foundation of Ministry of Education of China)

夏长青，博士研究生，从事软黏土力学和地基处理研究；E-mail: xiacq09@163.com

(编辑 杨幼平)