生物多样性指数的教学案例探讨
2018-08-08张青田马寅晖胡桂坤
张青田 马寅晖 徐 鑫 胡桂坤
(天津科技大学海洋与环境学院/天津市海洋资源与化学重点实验室 300457)
生物多样性指数是课堂教学的重要内容,也是科学实践的重要内容。熟悉不同生物多样性指数的特点和侧重点才能发挥其在环境评价中的应用价值,为在教学方式和方法方面进行积极探索,遴选适宜的教学案例有利于完成教学任务,为实践工作奠定坚实的基础。
1 生物多样性指数的教学要求
生物多样性是指所有来源的形形色色生物体,来源包括陆地、海洋和其他水生生态系统及其所构成的生态综合体。如何保护生物多样性是生命科学中急需要解决的热点问题之一。物种多样性指数是定量评价生物多样性现状并为其保护实践活动提供理论依据的重要工具[1]。在长期的研究过程中,人们创造了很多指数来表示生物多样性,如香农指数、均匀度指数、辛普森指数等。
生物多样性的意义通常包含两部分: 物种丰富度和均匀度。前者代表生物多样性最古老、最直观的测度,后者是描述物种多度的变异性。与均匀度相对的是优势度,即一个或几个物种在群落中占优势的程度。众多的多样性指数多关注丰富度和均匀度两者或其中之一。Clarks & Warwick[2]对不同多样性指数进行主成分分析后,得出的结论是: 代表丰富度和均匀度的前两个轴占据了总变异量的大多数。习惯上,人们对丰富度高和均匀度高是等同看待的[3]。
在教学中的一个重要目的是让学生明白指数的差别和侧重点,确保在实践中有效使用指数。为了实现教学目的,教学中应该注意讲解层次,分步骤讲清指数的侧重点。同时,必须强调学生的参与,引导学生发现问题。例如,设置问题引导学生比较不同指数的计算结果,总结传统指数的特点和局限;然后引出新的指数并思考,激励学生动手动脑,进入高阶学习的层次[4]。
2 教学案例分析
2.1 遴选生物群落 在教学中,先从实际调查的结果中遴选出一个底栖群落A进行分析。该群落共有7种生物,隶属于四门五纲七目。然后,由群落A模拟出新的群落B和C,用以比较几种生物多样性指数。其中,群落B的7种生物隶属于同属,群落C的7种生物隶属于同目的四个科(图1)。

图1 遴选出的生物群落的生物组成示意图
为了更好地理解多样性指数,以更丰富的情况引导学生深入学习,将上述A、 B、 C三个群落中7种生物的单位面积个体数(即丰度)再演绎出多种情况,并包含较特殊的情形。由此构成表1中的3个教学例子。
2.2 多样性指数 计算常用的指数包括香农指数(H′)、均匀度指数(J′)、马卡列夫丰富度指数(d)和辛普森指数(1-λ)等传统多样性指数,以及平均分类学差异性指数(Δ+)和分类学差异性变异指数(Λ+)。计算公式分别如下[2]: H′=-∑(Ni/N)×loge(Ni/N); J′=H′/logeS; d=(S-1)/logeN; 1-λ=1-∑(Ni/N)2; Δ+=2∑∑i 表1 生物群落中7种生物的组成情况(个/m2) 2.3 传统多样性指数计算结果与分析 以例1中群落A为例,计算辛普森指数,则1-λ=1-∑(10/70)2=1-(10/70)2×7=0.86(保留2位小数)。同理,将各个示例的数据分别代入前述公式计算4个传统多样性指数,得出结果(表2)。该过程由学生分别计算不同群落的多样性指数,再汇总到一起。这样既可以节省时间,又吸引学生参与到主动学习中,而且在对比结果时会有惊奇的效果。 表2 不同生物群落传统多样性指数计算结果 由表2可知: ①在例1至例3中,群落A、 B和C的4个传统多样性指数(H′、 J′、 d、 1-λ)的结果分别相同,表明这些指数在每个例子中未能区分开3个生物群落的多样性差异。②对于H′、 J′和1-λ这三个指数来说,3个例子中的多样性指数均呈现出降低的趋势。这表明指数的大小受生物均匀性影响较大,当生物个体数相等时有较高值,而某种生物优势度高时则出现较低值。而d值大小主要受总个体数的影响。此外,如果生物体个数都相同时,H′、 J′和1-λ的结果是一样的(如,7种生物的每一种个体数都是3个和例1中都是10个的计算结果完全一致)。 2.4 差异性指数计算结果与分析 前述4个传统多样性指数未能区分开A、 B、 C三个群落的多样性,与它们不区分生物类别有关。任何生物按照表中情形组合都会得到同样的结果。但事实上,不同生物在生态系统中的作用是不同的,不同生物组成的群落,其稳定性是有差异的。而这些传统指数没能完全客观地反映群落生物多样性的现状,难以为生物多样性保护提供足够的科学依据。为了更好地展示生物多样性,将分类学信息引入指数中是很有必要的,常用的有平均分类学差异性指数(Δ+)和分类学差异性变异指数(Λ+)。由于这两个指数加入了生物差异性权重[2, 5],即ωij,故在实践中显示出良好的应用效果。 在计算时,考虑生物隶属的门类信息,将分类树中最高阶元的路径定义为100,然后按照比例确定其他阶元的路径距离。以图2为例,最高阶元为科,包括3属5种生物,每种生物有1~4个个体。则同科不同属的生物x3和x4之间的路径距离为100,同属的x1和x2之间则为50。该指数忽略同种生物个体间的差异,故物种x5的不同个体间距离为0。其他生物的权重均可依此计算,然后代入公式。 图2 分类学多样性指数的权重示意图 在上述教学案例(图1)计算时,从“门”至“属”5级阶元之间的权重按比例分别定为100、 83.3、 66.7、 50、 33.3和16.7。不同门的生物权重最高,为100;同属的生物权重最低,为16.7。以图1中的物种S1和S7为例,在群落A中权重为100,在群落B中权重仅为16.7,而在群落C中的权重为50。权重参数将生物的分类学信息带入了多样性指数公式。计算结果见表3。 表3 分类学差异性指数和差异性变异指数计算结果 由表3可知,Δ+和Λ+指数在3个示例中均区分开了群落A、 B和C的多样性情况,与4个传统多样性指数明显不同。群落A的Δ+值(93.65)明显高于其他群落,群落B具有最低的Δ+(16.67)和Λ+值(0)。Δ+值主要反映生物在分类学多样性方面的信息,数据高则可以认为群落多样性较好;Λ+则表示生物分类地位的变化,数值越小则变化越小,生物亲缘关系越近(同时要关注Δ+大小)。这两个指数的结果反映出3个群落的不同,这和人们对这三个群落组成的直观认识是基本一致的。 同时可以看到,Δ+和Λ+指数的结果在3个例子中是依次重复的(表3),这是由指数的性质决定的。这两个指数忽略生物丰度,不受取样时间、地点和样方大小的影响,而且只需要生物名录即可进行生物多样性指数的计算和比较。很多研究证明了这是该指数的优势,这里不赘述。 任何生物的生存都会在争夺有限的生活条件时进行竞争。一般来说,同属物种间的竞争会更激烈,这样的群落不稳定。通常情况下,人们认为群落A的多样性和稳定性要高于其他两个,而群落B的多样性最低。因此,平均分类学差异性指数能够更好地反映出群落状况,为环境保护或生态修复提供依据。 必须注意,所有生物多样性指数都属于单变量分析的范畴,相当于将复杂的生物组成情况降为一维的结果。在降维过程中肯定要损失很多信息,也就注定了每种指数都有其优点和不足。在使用中应该注意多种指数的综合分析。 教学中应注意知识层次,把一些多样性指数串联起来,这样有利于类似知识的学习和比较。同时,积极激励学生参与到教学中,能更有效地完成教学任务。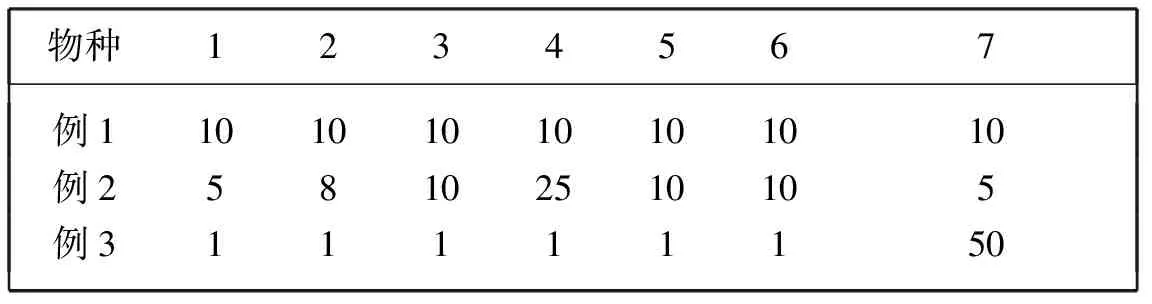



3 小结
