利用贝叶斯定理分析遗传病的发病率

杨 维

(山东省枣庄市第三中学 277100)

1 贝叶斯定理简介

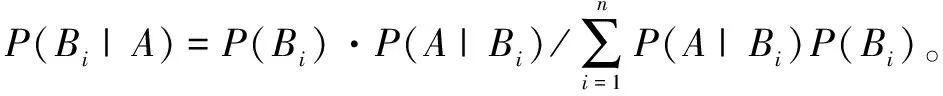
2 贝叶斯定理的应用

例题： 科学家研究发现，β珠蛋白基因的突变是导致镰刀型细胞贫血症的元凶。该突变导致β珠蛋白中正常的谷氨酸变成了缬氨酸。在某地区人群中有4%的人是该病患者，会在成年之前死亡，有32%的人是携带者，不发病。图1是某家族镰刀型细胞贫血症的遗传系谱图。(注： Ⅱ5为该地区男性，镰刀型细胞贫血症基因为A、a)根据上述资料，回答下列问题： 若Ⅲ2与Ⅲ3婚配，生育的子女中患镰刀型细胞贫血症的几率是： 。

图1 某家族镰刀型细胞贫血症遗传系谱图

2.1 依据遗传定律进行计算 Ⅱ4的父母基因型均为Aa，Ⅱ4有两种可能性： AA(占1/3)或Aa(占2/3)。Ⅱ5根据人群中患者及携带者的比例，可知他的基因型也有两种可能性： AA(占2/3)或Aa(占1/3)。故Ⅱ4与Ⅱ5婚配组合情况及概率为： ①有1/3×2/3=2/9的可能为Ⅱ4AA×Ⅱ5AA；②有1/3×1/3=1/9的可能为Ⅱ4AA×Ⅱ5Aa；③有2/3×2/3=4/9的可能为Ⅱ4Aa×Ⅱ5AA；④有2/3×1/3=2/9的可能为Ⅱ4Aa×Ⅱ5Aa。

由此计算，那么Ⅲ3是AA的可能性为10/17，是Aa的可能性为7/17。Ⅲ2与Ⅲ3婚配后代患镰刀型细胞贫血症的概率为7/34。

但在Ⅲ3与Ⅲ4均不患病的情况下，Ⅱ4与Ⅱ5上述四种组合的概率将会有所变化(需要重估)。

2.2 利用贝叶斯定理对Ⅱ4与Ⅱ5婚配组合概率进行重估 由于Ⅱ4与Ⅱ5生的两个孩子都是正常的。按照贝叶斯定理此时的事件A为Ⅱ4与Ⅱ5生的两个孩子都是正常的，相关计算如表1。故Ⅱ4与Ⅱ5婚配组合情况及概率更正为： ①有16/65的可能为Ⅱ4AA×Ⅱ5AA；②有8/65的可能为Ⅱ4AA×Ⅱ5Aa；③有32/65的可能为Ⅱ4Aa×Ⅱ5AA；④有9/65的可能为Ⅱ4Aa×Ⅱ5Aa。重估之后，Ⅲ3是AA的可能性为153/251，是Aa的可能性为98/251。Ⅲ2与Ⅲ3婚配后代患镰刀型细胞贫血症的概论为98/502。

2.3 若Ⅱ4与Ⅱ5所生的n个孩子均未患病 按照贝叶斯定理，此时的事件A为Ⅱ4与Ⅱ5生的n个孩子都是正常的，相关计算如表2。

表1 Ⅱ4与Ⅱ5婚配组合的概率计算(Ⅱ4×Ⅱ5)

表2 Ⅱ4与Ⅱ5婚配组合的概率计算(Ⅱ4×Ⅱ5)

故Ⅱ4与Ⅱ5婚配组合情况及概率应为： ①有2/[7+2(3/4)n]的可能为Ⅱ4AA×Ⅱ5AA；②有1/[7+2(3/4)n]的可能为Ⅱ4AA×Ⅱ5Aa；③有4/[7+2(3/4)n]的可能为Ⅱ4Aa×Ⅱ5AA；④有2(3/4)n/[7+2(3/4)n]的可能为Ⅱ4Aa×Ⅱ5Aa。由此计算，那么Ⅲ3是Aa的可能性为[5+2(3/4)n]/[7+3(3/4)n]。Ⅲ2与Ⅲ3婚配后代患镰刀型细胞贫血症的概率为[5+2(3/4)n]/2[7+3(3/4)n]。

3 小结

根据分析发现，利用贝叶斯定理计算的遗传病发病率要低于依据遗传定律计算的结果。相关研究认为，利用贝叶斯定理计算的发病率更加精确，且目前已经广泛应用于临床的遗传咨询[1]和医学院校遗传学的教学中[2]。但这不能说明根据遗传定律计算的发病率是错误的，在高中生物学教学中，教师在讲授基于遗传定律计算遗传病发病率的基础上，可以向学有余力的学生介绍贝叶斯定理及其应用，以拓展学生的视野。