量子遗传算法在变压器故障诊断模型中的应用
2018-08-06龚瑞昆周国庆
龚瑞昆 周国庆
摘 要: 传统的BP神经网络诊断模型容易陷入局部最优,且诊断正确率较低,因此,提出将量子遗传算法应用于RBF网络诊断模型。首先确定RBF神经网络的输入输出、建立RBF网络模型,然后把归一化后的数据送入RBF网络模型,利用量子遗传算法对RBF神经网络进行优化,得到最优诊断模型,最后输出诊断结果。用Matlab进行仿真,其结果表明该算法解决了系统容易陷入局部最优的问题,在训练48代后就快速获得最优解,加快了网络的收敛速度。同时RBF神经网络的泛化能力也得到很好的改善,故障诊断正确率达93%,远远高于传统神经网络模型。
关键词: 变压器; 故障诊断; BP神经网络; 量子计算; RBF神经网络; 量子遗传算法
中图分类号: TN98?34; TP391.9 文献标识码: A 文章编号: 1004?373X(2018)15?0129?04
Application of quantum genetic algorithm in transformer fault diagnosis model
GONG Ruikun, ZHOU Guoqing
(North China University of Science and Technology, Tangshan 063000, China)
Abstract: The traditional BP neural network diagnosis model is easy to fall into local optimum, and has low diagnostic accuracy. Therefore, the quantum genetic algorithm is applied to RBF network diagnosis model, with which the input and output of RBF neural network are determined to establish the RBF diagnosis model, the normalized data is sent to the RBF diagnosis model. The quantum genetic algorithm is used to optimize the RBF neural network to obtain the optimal diagnostic model and output the diagnosis result. The Matlab simulation results show that the algorithm can solve the problem that the system is easy to fall into local optimum, obtain the optimal solution after training 48 generations, and speed up the network convergence rate. The generalization ability of RBF neural network is improved greatly, the fault diagnosis accuracy can reach up to 93%, which is much higher than that of the tradition neural network model.
Keywords: transformer; fault diagnosis; BP neural network; quantum computing; RBF neural network; quantum genetic algorithm
0 引 言
变压器的运行状态是否正常至关重要,因为它决定了整个电力系统是否能够正常运行,所以我们要避免和减少变压器故障的发生[1]。但是由于变压器结构比较复杂,传统的三比值法和色谱分析法不能准确地反映出故障类型和特征气体之间的关系[2]。
对于变压器故障诊断多用BP神经网络算法。但是BP神经网络的搜索求解算法是沿梯度下降,所以当学习样本的数目较多、输入输出比较复杂时,容易陷入局部极小值,且收敛速度慢[3]。针对上述问题,本文提出将量子遗传算法应用于RBF神经网络诊断模型。
1 RBF神经网络
1.1 RBF神经网络基本原理
径向基函数(RBF)神经网络结构相对简单,学习能力强,而且有唯一最佳逼近值,具有较好的全局逼近能力[4]。由于RBF神经网络训练方法快速易行,不存在局部最优,所以在故障诊断、模式识别等领域广泛应用。
1.2 RBF神经网络结构
RBF神经网络结构如图1所示。第一层是输入层;第二层是唯一的隐含层;第三层为输出层,它是线性的。通常RBF神经网络选取高斯函数为其径向基函数。
假定该网络输入层的训练样本输入为[Xn=][xn1,xn2,…,xnMTn=1,2,…,N];训练样本期望输出为[dnn=1,2,…,N],对应实际输出为[Ynn=1,2,…,N]。
第[i]个隐单元的输出为[?Xn,ti],[?Xn,ti]为基函数,它的中心为:
[ti=ti1,ti2,…,tiM, i=1,2,…,I] (1)
设[wii=1,2,…,I]为第[i]个隐单元和输出单元的连接权值,则網络的实际输出为:
[YnXn=i=1Iwi?Xn,ti] (2)
2 量子遗传算法
量子遗传算法是把比特位用量子位表示[5]。把量 子概念融入遗传算法,大大提高了遗传算法搜索速度。为了使进化过程中的隐含信息得以全面利用,根据父代中的最优个体和它的概率幅值选择后代,进一步提高进化速度,利用量子的旋转门实现遗传操作。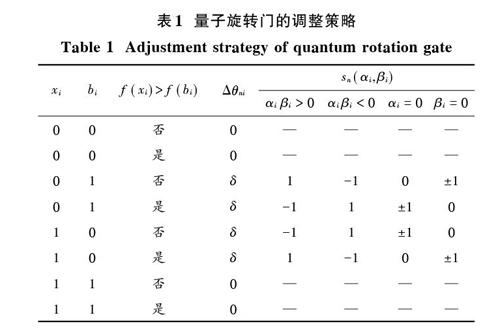
假定一条染色体有[m]位量子比特,一位量子比特的状态为复数对[α,β],则染色体编码由[m]个复数对组成。单个染色体编码形式为[P=p1p2…pm],其中[pi=αi,βiT],[1≤i≤m]。
经[n]次迭代后,第[i]个量子门的旋转门为:
[Gn,i=cos θni-sin θnisin θnicos θni] (3)
式中:[θni]为旋转角且[θni=snαi,βi],[snαi,βi]为旋转方向;[Δθni]为旋转角度,其值由表1确定。
量子遗传操作实现步骤如下:
[pn+1i=Gn,ipni, 1≤i≤m] (4)
设[xi]为某个个体的解[x]的第[i]个量子位所对应的二进制位。[bi]为当前最优个体[b]的第[i]个量子位所对应的二进制位。个体当前测量值的适应度为[fxi],最优个体测量值的适应度为[fbi],比较[fxi]和[fbi]的大小:若[fxi>fbi],则调整[pnj]中相应位的量子比特[xi≠bi],使[αi,βi]向有利于[xi]的出现变化;若[fxi 文献[6]提出量子交叉干扰操作,具体的过程为:在表2中,取编号1染色体第1位,编号2染色体第2位,按照这种方法依次取后面的基因,直到新个体与原个体的基因数相同为止,确定干扰后的第一個染色体为[A0]?[B1]?[C2]?[D3]?[E4];依照同样的方法确定其他新个体,直到与原种群规模相同,则结束交叉操作。 当连续迭代次数达到某一值且最优解不变时,则陷入局部极小点,所以要对算法进行灾变操作。实现过程为:保留最优解,除此以外的个体采用上述交叉方法生成。
3 RBF神经网络故障诊断模型构建
3.1 变压器故障诊断原理
变压器发生不同的故障时,油中溶解气体浓度就会发生相应的变化,所以可以通过分析这些气体的浓度判断变压器的潜在问题和故障情况[7]。由于变压器故障受多种因素的影响,每个因素对其作用的函数关系又难以确定,所以变压器故障诊断属于复杂的非线性系统问题,因此,应采用RBF神经网络建立故障诊断模型,其原理如图2所示。将归一化后的数据送入RBF诊断模型中,利用量子遗传算法优化RBF神经网络的参数,得到优化后的最优诊断模型,最后输出变压器的诊断结果。
3.2 RBF神经网络输入输出的确定
当电力变压器运转不正常时,油中溶解气体的产生速率将会变快。因为变压器发生不同的故障时,油中溶解气体浓度就会发生相应的变化,所以根据油中溶解的特征气体[H2],[CH4],[C2H2],[C2H4],[C2H6]的体积百分数分析变压器为哪种故障。由于这些特征气体的体积百分数量值差别比较大,为了使网络有较好的收敛性,将输入的数据进行归一化处理。也就是把每种特征气体含量占5种特征气体总量的百分比作为RBF神经网络的输入向量,所有输入量都在0和1之间。网络的输入向量为:
[Xi=xi1,xi2,xi3,xi4,xi5T] (5)
式中[xi1]~[xi5]分别表示变压器油中[H2],[CH4],[C2H2],[C2H4],[C2H6]归一化之后的值,归一化公式为:
[xij=xiji=15xij, i=1,2,…,n] (6)
把变压器的故障类型作为RBF神经网络的输出向量,变压器的主要故障有四种,因此,输出向量为4个输出神经元,[F1]表示中低温过热、[F2]表示为高温过热、[F3]表示低能量放电、[F4]表示高能量放电。
3.3 量子遗传算法对RBF网络的优化
设样本为[N],输出的神经元个数为[M],误差[e=e1,e2,…,eNM],则误差的平方和为:
[E=12i=1NMe2i] (7)
式中[ei]为样本在输出层的某个神经元上的误差。
算法如下:
1) 初始种群的产生。设最大迭代代数为[E1]、灾变代数为[E2]、种群个体数目为[Ng],则初始种群[Q=p1,p2,…,pNg],神经网络每个权值/阈值有10个量子位。[pi]见式(4),表示第[i]个神经网络权值/阈值的编码组合,[1≤i≤Ng],其中[αi],[βi]均为[12]。设当前迭代次数[E3=0]。
2) 种群的测量。采用在[0,1]间产生随机数的方法将量子比特转化为比特,则[pi]变为二进制串。如果量子比特概率的平方比随机数大则为1,如果比随机数小则为0。
3) 种群的评价。将式(7)作为适应值函数对每个个体进行评价,并保留最优个体。
4) 交叉操作。判断是否符合收敛条件,若符合则停止操作,若不符合则继续进行交叉操作。
5) 量子旋转门操作。用式(4)调整种群中所有个体,根据表1调整旋转角。
6) 灾变操作。连续迭代[E2]代,若最优个体不变,则进行此操作,否则继续。
7) [E3=E3+1],若[E3≥E1,]则算法结束,否则执行步骤2)。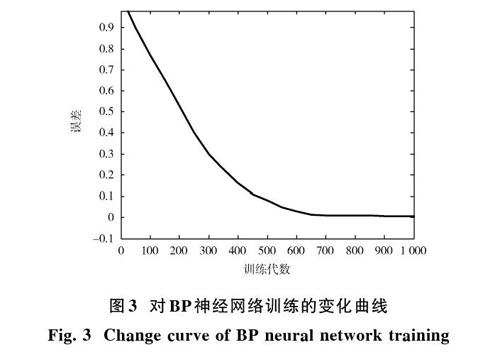

4 仿真研究
收集四种故障类型油样共100组,来源为发电厂和研究院。使用Matlab软件进行仿真,首先设计优化后的RBF神经网络故障诊断模型,再设计BP神经网络模型与之做对比。用收集到的样本对神经网络进行训练,训练目标为平均一个样本误差平方和小于0.01,故障诊断正确率統计如表3所示。从表3中可以看出,采用量子遗传算法优化后的RBF网络诊断模型具有较高的诊断性能。
两种神经网络训练误差随训练次数的变化曲线如图3,图4所示。由两图对比,明显观察到采用BP神经网络的训练次数多,且收敛速度慢;采用量子遗传算法优化的RBF神经网络进行训练,快速收敛的性能得以很好地表现出来,在训练48代后就快速获得最优解。
5 结 论
由于变压器的故障与多种因素有关,较为复杂,所以传统的BP神经网络诊断模型容易陷入局部最优,且诊断正确率较低。本文提出将量子遗传算法应用于RBF网络诊断模型,结果表明:
量子遗传算法有效利用量子态和量子门操作,能有效获得RBF神经网络可变参数的全局最优附近的解,且收敛速度快。RBF神经网络的泛化能力得到很好的改善,并且相比于一般网络,其对变压器的诊断效果有明显提升。
参考文献
[1] 刘宾.电力变压器的故障诊断与风险评估[D].济南:山东大学,2013.
LIU Bin. Fault diagnosis and risk assessment of power transformers [D]. Jinan: Shandong University, 2013.
[2] 李梦醒.如何应用油中溶解气体分析法判断变压器故障方法[J].现代国企研究,2016(24):162.
LI Mengxing. How to use the dissolved gas analysis method in oil to determine transformer faults [J]. Modern state?owned enterprise research, 2016(24): 162.
[3] 禹建丽,卞帅.基于BP神经网络的变压器故障诊断模型[J].系统仿真学报,2014,26(6):1343?1349.
YU Jianli, BIAN Shuai. Transformer fault diagnosis model based on BP neural network [J]. Journal of system simulation, 2014, 26(6): 1343?1349.
[4] 吴宏岐,周妮娜,王春英.基于RBF神经网络的变压器故障诊断及MATLAB仿真研究[J].科学技术与工程,2010,10(5):1249?1251.
WU Hongqi, ZHOU Nina, WANG Chunying. Fault diagnosis and Matlab simulation of transformer based on RBF neural network [J]. Science, technology and engineering, 2010, 10(5): 1249?1251.
[5] 梁昌勇,柏桦,蔡美菊,等.量子遗传算法研究进展[J].计算机应用研究,2012,29(7):2401?2405.
LIANG Changyong, BAI Hua, CAI Meiju, et al. Progress in quantum genetic algorithms [J]. Application research of compu?ters, 2012, 29(7): 2401?2405.
[6] 李胜,张培林,李兵,等.基于通用量子门的量子遗传算法及应用[J].计算机工程与应用,2017,53(7):54?59.
LI Sheng, ZHANG Peilin, LI Bing, et al. Quantum genetic algorithm based on universal quantum gate and its application [J]. Computer engineering and applications, 2017, 53(7): 54?59.
[7] 李红卫.变压器油化验技术分析及影响[J].中国高新技术企业,2016(1):55?57.
LI Hongwei. Analysis and influence of transformer oil testing technology [J]. China high?tech enterprise, 2016(1): 55?57.
[8] 朱紫娟.综合故障诊断方法在电力变压器故障诊断中的应用研究[D].西安:西安工程大学,2016.
ZHU Zijuan. Application of comprehensive fault diagnosis method in fault diagnosis of power transformer [D]. Xian: Xian Polytechnic University, 2016.
[9] 赵越,茹婷婷.遗传算法理论与应用新探[J].轻工科技,2014,30(1):77?78.
ZHAO Yue, RU Tingting. A new probe into the theory and application of genetic algorithm [J]. Light industry technology, 2014, 30(1): 77?78.
[10] 马颖.基于量子计算理论的优化算法研究[D].西安:西北工业大学,2014.
MA Ying. Research on optimization algorithm based on quantum computing theory [D]. Xian: Northwestern Polytechnical University, 2014.
[11] 周殊,潘炜,罗斌,等.一种基于粒子群优化方法的改进量子遗传算法及应用[J].电子学报,2006(5):897?901.
ZHOU Shu, PAN Wei, LUO Bin, et al. An improved quantum genetic algorithm based on particle swarm optimization and its application [J]. Acta electronica sinica, 2006(5): 897?901.
[12] 王俊宁,姚莉.电力变压器常见故障及在线监测技术分析[J].科技创新与应用,2014(13):141.
WANG Junning, YAO Li. Analysis of common faults and online monitoring techniques of power transformers [J]. Technological innovation and application, 2014(13): 141.
[13] 张岩.电力变压器常见故障及在线监测技术分析[J].黑龙江科技信息,2014(30):73.
ZHANG Yan. Analysis of common faults and online monitoring techniques of power transformers [J]. Heilongjiang science and technology information, 2014(30): 73.
