子阵级ADL?MVDR自适应波束形成算法

费晓 张贞凯 田雨波

摘 要： 大型面阵的阵元数量较大，导致全自适应波束形成的计算量显著增长，通过子阵级波束形成则可以进一步降低算法运算量。研究常规面阵的非均匀子阵波束形成技术，在常规MVDR算法的基础上，引入自适应对角加载ADL技术，提出基于MVDR?ADL的子阵波束形成算法，避免栅瓣的产生，进一步抑制噪声的影响。仿真结果表明，所提算法在降低方向图旁瓣电平的同时，进一步减少了算法的运行时间。

关键词： 子阵； 面阵； 旁瓣； 自适应对角加载； 波束形成； 栅瓣

中图分类号： TN957?34 文献标识码： A 文章编号： 1004?373X（2018）15?0069?04

Adaptive beamforming algorithm based on ADL?MVDR at sub?array level

FEI Xiao， ZHANG Zhenkai， TIAN Yubo

（School of Electronics and Information， Jiangsu University of Science and Technology， Zhenjiang 212003， China）

Abstract： The calculation amount of adaptive beamforming is greatly increased due to the large number of array elements in the planar array， which can be further reduced by means of beamforming at sub?array level. The non?uniform sub?array beamforming technique for the conventional planar array is studied in this paper. On the basis of conventional minimum variance distortion response （MVDR） algorithm， the adaptive diagonal loading （ADL） technique is introduced， and the adaptive beamforming algorithm based on ADL?MVDR at sub?array level is proposed to avoid the generation of grating lobe and further suppress the noise influence. The simulation results show that the proposed algorithm can further shorten the running time of the algorithm while deducing the sidelobe level of directional diagram.

Keywords： sub?array； planar array； sidelobe； adaptive diagonal loading； beamforming； grating lobe

0 引 言

國内外学者对ADBF（Adaptive Digital Beamforming）的研究、改进已有三十多年，但绝大多数的成果都基于阵元级。在ADBF技术中，全自适应处理是最有灵活性的设计方法，即各个阵元对应一个接收通道。但大型相控阵的阵列包含的阵元数量庞大，如果采用全自适应方法，会导致系统复杂度增加，硬件成本上升，难以达到实质性需求。若把该阵列上的阵元按照子阵划分方案分成多个子阵，每个子阵与对应的接收通道相连，最后进行波束形成，不仅使运算量下降、收敛速度加快，还能使成本大大降低。

对子阵级ADBF算法的研究大多是以一维线阵进行的，文献[1]对线阵的子阵结构提出了非均匀构阵原则。针对子阵级时的旁瓣升高，文献[2]提出基于罚函数和特征空间的子阵级波束形成算法。文献[3]通过对子阵多波束输出的协方差矩阵求平均提高算法的性能。文献[4]提出采用归一化方法来降低子阵旁瓣电平，但对于实际的相控阵，基本采用平面阵结构，所以在系统性能方面，如果子阵级ADBF能够应用在平面中，对其具有重要意义。MVDR（Minimum Variance Distortion Response）是一种常用的波束形成算法[5]，当它运用到子阵级时，主瓣方向容易变形。本文对基于ADL?MVDR子阵波束形成进行研究，建立信号模型，在一维线阵、平面阵上分别提出ADL?MVDR子阵级算法。与常规MVDR子阵级算法相比，本文提出的算法具有较好性能，同时进一步降低了运算量。

1 信号模型及子阵处理

1.1 信号模型

平面阵由M个全向阵元组成，各阵元位于[xOy]平面上。其中以坐标原点阵元为第1个阵元，并设为参考阵元，第m（m=1，2，…，M）个阵元的坐标为[（xm，ym）]。[wm]表示阵元级中第[m]个阵元的幅度加权，通过移相器实现波束指向。仰角、方位角用[（θ，φ）]表示，[（θ0，φ0）]为波束指向，有[K]个窄带干扰，[（θk，φk）]为第[k]（[k]=1，2，…，[K]）个干扰方向。

式中：[s（t）=[s1（t），s2（t），…，sk（t），…，sK（t）]T]，且[sk（t）]为第一个阵元接收到的第[k]个窄带干扰源的复包络；[n（t）=[n1（t），n2（t），…，nm（t），…，nM（t）]T]，[nm（t）]为第[m]个阵元中与干扰不相关的高斯加性白噪声[6]。同时设每一个阵元输出的噪声功率均为[δ2n]。

1.2 子阵处理

平面阵含有[P*Q]个阵元，顺着[x]轴和[y]轴划分成[M*N]个子阵，通过矩阵[T]能够对子阵进行划分[7]，[T]为[（P*Q）*（M*N）]维的降维矩阵：

2 基于ADL?MVDR子阵级波束形成算法

首先考虑常规MVDR子阵级算法，用[Wsub]表示子阵级最优加权向量，采用MVDR准则[9]时，[Wsub]应该满足以下极值方程条件：

在理想条件下，虽然MVDR子阵级算法能将主瓣波束对准期望信号的同时最大程度地抑制干扰和噪声，但MVDR子阵级算法有它的缺点：该算法比较依赖期望信号的波达方向，对波达方向的误差敏感，容易产生子阵级权矢量的计算误差，波束性能会有所下降。所以在实际的子阵波束形成过程中，必须将这些误差带来的性能损失问题考虑进去。

对于小特征值对应的噪声波束，自适应对角加载能减弱它的影响，把损失降低，同时出于对运算量、收敛速度和成本问题的考虑[10]，本文算法在子阵级上采用自适应对角加载技术，它能有效改善阵列方向图的形成，降低旁瓣。相比于阵元级自适应对角加载技术，改进后的子阵波束形成运算量减小、收敛速度加快，还能使成本大大降低。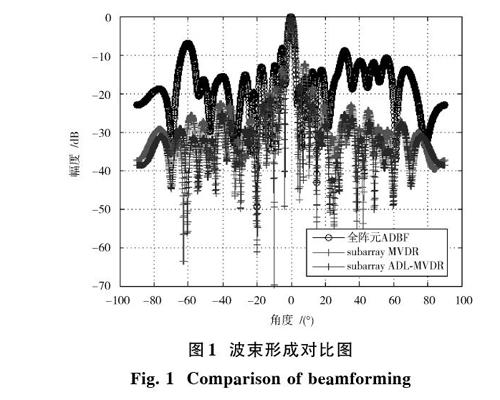

3 仿真结果

仿真1：取均匀线阵模型，阵元数N=32，阵元间距d为半波长，在子阵级上采用-40 dB泰勒加权，划分方案为[5，3，2，2，6，4，6，4]，划分8个子阵，信号和干扰均为窄带，主瓣波束指向0°，干扰方向为（-20°，15°），干噪比为30 dB，噪声为平稳零均值的带限高斯过程，各噪声之间相互独立，且与信号不相关，快拍数为500。

一维均匀线阵自适应子阵波束形成技术仿真结果如图1所示。通过仿真对比可知，三种算法都能在干扰方向形成零陷，而ADL?MVDR算法则进一步对干扰进行抑制，全阵元ADBF和常规MVDR子阵级波束形成算法形成的旁瓣电平都相对较高，通过ADL?MVDR子阵级波束形成算法改进后波束的旁瓣电平进一步下降，ADL?MVDR算法能够根据接收信号协方差矩阵的特征结构，在不同信噪比条件下自适应地加载对角线，可进一步抑制波束方向图畸变，且在非均匀划分结构下，均无栅瓣出现。

仿真2：选取平面阵模型，设行列阵元数均为32，各阵元放置在矩阵网格中，x和y方向的阵元间距均为半波长，阵列按照子阵划分方式划分为8[×]6个子阵，各子阵均为矩形阵。

子阵级在x，y方向进行-40 dB泰勒加权，设（0°，0°）为期望信号的俯仰角与方位角，确知一个窄带干扰信号，俯仰角与方位角为（40°，40°），干噪比为30 dB。天线在（-90°，90°）范围内扫描。得到的平面阵自适应子阵波束形成方向图如图2，图3所示。

对比图2，图3可以看出，相比于常规子阵级算法，本文的ADL?MVDR子阵级算法能够得到较好的旁瓣抑制效果。因为采用非均匀子阵划分方案，波束中无栅瓣生成。子阵级自适应对角加载改善了自适应波束形成中的一个重要问题，即波束形成的性能。

在相同实验环境下，子阵级MVDR算法运算时间为253.08 s，而子阵级ADL?MVDR算法运算时间为137.091 s。在性能方面，后者的仿真速度更加快速高效。

4 结 论

为了进一步降低算法运算量和改善波束性能，本文在常规MVDR算法的基础上引入自适应对角加载技术，提出基于MVDR?ADL的子阵波束形成算法。实验仿真表明，在非均匀子阵划分方案下，旁瓣电平得到改善，同时算法的运行时间进一步减少，具有一定的研究价值和研究意义。

参考文献

[1] NICKEL U R O. Subarray configurations for digital beamforing with low sidelobes and adaptive interference suppression antenna [C]// 1995 IEEE International Conference on Radar. Alexandria： IEEE， 1995： 714?719.

[2] 杨小鹏，张宗傲，孙雨泽，等.基于罚函数和特征空间的子阵级自适应波束形成[J].北京理工大学学报，2016，36（5）：541?545.

YANG Xiaopeng， ZHANG Zongao， SUN Yuze， et al. Adaptive beamforming at sub?array level based on penalty function and function and eigen?space [J]. Transactions of Beijing Institute of Technology， 2016， 36（5）： 541?545.

[3] 乔永雯，杨益新，孙超.子阵波束域自适应波束形成方法研究[J].船舶工程，2007，29（4）：75?78.

QIAO Yongwen， YANG Yixin， SUN Chao. Study on self?adap?ting beam forming in the sub?array beam [J] Ship engineering， 2007， 29（4）： 75?78.

[4] 赵红，刘桥.一种低旁瓣的子阵级数字波束形成方法[J].兵工自动化，2009，28（11）：65?68.

ZHAO Hong， LIU Qiao. Subarray digital beamforming method with a low sidelobes [J]. Ordnance industry automation， 2009， 28（11）： 65?68.

[5] 葛佩，李明，刘翔.一种低旁瓣子阵级自适应波束形成方法[J].雷达科学与技术，2012，10（5）：519?523.

GE Pei， LI Ming， LIU Xiang. An adaptive beamforming method at subarray level for planar array with low sidelobes [J]. Radar science and technology， 2012， 10（5）： 519?523.

[6] 曾操，陈昊，何学辉，等.相控阵子阵级和差多波束测角方法[J].西安电子科技大学学报（自然科学版），2013，40（1）：19?25.

ZENG Cao， CHEN Hao， HE Xuehui， et al. Monopulse angle estimation using sum?difference multi?beamforming based on the phasedarray at the subarray level [J]. Journal of Xidian University （natural science edition）， 2013， 40（1）： 19?25.

[7] 张小飞.阵列信号处理的理论和应用[M].北京：国防工业出版社，2014.

ZHANG Xiaofei. Theory and application of array signal proces?sing [M]. Beijing： National Defence Industry Press， 2014.

[8] 潘点飞，程乃平，郝建华.平面阵子阵级自适应波束形成方法研究[J].雷达科学与技术，2014，12（3）：304?310.

PAN Dianfei， CHENG Naiping， HAO Jianhua. Research on adaptive beamforming method at subarray level for planar array [J]. Radar science and technology， 2014， 12（3）： 304?310.

[9] 朱承龙.基于子阵列的阵列发射波束形成方法研究[D].成都：电子科技大学，2015.

ZHU Chenglong. Research on beam forming method at sub array level [D]. Chengdu： University of Electronics Science and Technology of China， 2015.

[10] 高杨，李东生.基于改良MUSIC和ADL?LC MV的自适应波束形成算法[J].探测与控制学报，2015，37（3）：24?28.

GAO Yang， LI Dongsheng. Adaptive beamforming algorithm based on modified music and ADL?LCMV [J]. Journal of detection & control， 2015， 37（3）： 24?28.