基于排序运动算法的选择装配技术

2018-08-06方喜峰吴家家

江苏科技大学学报(自然科学版) 2018年3期

方喜峰,张攀,张辉,吴家家

(江苏科技大学机械工程学院,镇江 212003)

选择装配是通过检测和挑选待装配零件,有选择性地进行装配,以达到较高装配精度的一种装配方法[1]．传统的选择装配方法主要有:直接选配法，分组选配法[2-3]，复合选配法．这3种选配方法虽然在一定程度上可以保证装配精度的要求,但是都依赖于装配工人的技术水平和经验,装配时间不易控制,影响产品的生产节拍．

随着计算机技术的发展,计算机辅助选择装配技术成为学者研究的热点．文献[4]利用蚁群算法解决了线性和径向两个方向尺寸误差的选择装配问题．文献[5]针对气缸活塞的装配要求,提出利用非支配排序遗传算法完成各零件间的选择装配．文献[6-8]提出利用加权法、粒子群算法、遗传算法,解决了多尺寸链选择装配问题;文献[9]提出一种基于SPEA 2的复杂机械产品多目标多质量要求下的选择装配方法．上述计算方法有效地解决了精密匹配耦件的选择装配问题,但是忽略了相同匹配数目和不同匹配数目耦件的两种情况下算法计算的复杂度问题．

针对以上问题以及当前企业对操作方便、易用的精密耦件选择装配系统的需求,文中以实际装配公差精度为目标,结合最优匹配的规则,运用排序运动算法实现对船用柴油机机架孔和气缸套的最优选择装配．

1 选配指标与规则制定

1.1 选配指标制定

针对复杂装配产品的选配指标制定,文献[10-12]考虑产品的加工成本和实际装配精度两方面因素,制定了多目标要求下的评价指标．但是从上海某国企的装配车间的实际调研中发现,所有选配部件的尺寸数据都是来自于制造执行系统，零部件尺寸在录入时,都是符合普通经济加工精度的产品．因此从企业生产的实际情况出发,将两组配合耦件的实际装配公差精度Q={q1,q2,…,qn}作为评价指标,实际装配公差精度Q的定义如下:

qi=Di-dii=1,2,3,…,n

(1)

式中：Di为参与配合的孔的第i个零件装配部位的尺寸,di为参与配合的轴的第i个零件装配部位的尺寸．

1.2 选配规则制定

在概率论中,通常用方差来度量随机变量和其数学期望(即均值)之间的偏离程度．文献[13-16]分别将方差作为图片质量和声波变换的评价指标,分析图像、声波在变换前后的细节信息,取得了较好的效果．文中采用方差作为衡量实际装配方差精度Q(Q∈R)与最优装配精度φ(φ∈R)的偏离程度,并建立评价函数F为:

(2)

2 排序运动算法的基本原理

排序运动算法的计算过程可以划分为排序和运动两个核心.排序是让两组零件的匹配数据按照从小到大的顺序进行排列;运动是在两组零件的匹配数据排序完成之后,在两组零件数据的数目不相同的情况下,让零件数据相对少的那一组数据在零件数据多的那一组数据的匹配位置上移动,在移动的过程中通过检测整体匹配的方差,求出整体匹配序列的最优位置,即最优匹配序列．

2.1 两组相同数量的数据排序最优匹配

定义1:在获得的两组需要匹配的零件数据的数量相同的情况下,整体的最优匹配序列则是两组数据分别按照从小到大的顺序排列后的序列．

设匹配组件α中有5个匹配件,零件尺寸分别为[a,b,c,d,e],另一组匹配组件β中也有5个匹配件,零件尺寸分别为[f,g,h,i,j],两组匹配数据按照从小到大的顺序排列后的序列如下:

如果原匹配序列不为最优匹配序列,则可以假设任意交换一组数据中两个尺寸值的位置后的序列为最优匹配序列,此处通过交换第二组尺寸数据g和f的位置,交换后的匹配序列如下:

利用交换尺寸数据前后的匹配序列整体方差值的正负可以判断原匹配序列是否为最优匹配序列．

交换前-交换后=

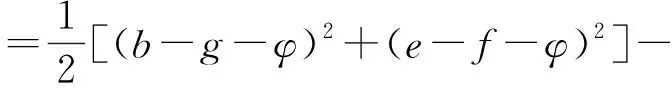
(3)

由原序列可知e≥b,g≤f,所以(e-b)(g-f)≤0,所以方差在交换前是小于或等于交换后的,也即证明了定义1的正确性．

2.2 两组不同数量的数据排序运动最优匹配

当获得的两组匹配数据的数量不一致时,仅通过数据的排序则无法让数量少的那一组尺寸数据在数量多的那一组尺寸数据上各自找到匹配序列整体最优的位置,因此需要让数量少的那组数据在数量多的那组数据的匹配位置上移动,在运动的过程中找到最优位置．

算法将数量少的那组数据确定为第一组数据,并将第一组数据整体向右移动,比较移动前后整体的方差值,如果移动前的方差值大于或者等于移动后的方差值,则记录移动后的位置,直至移动到第二组数据的末端．

整体局部最优算法流程如图1.

图1 排序运动算法整体局部最优流程Fig.1 Flowchart of overall local optimal of the sort and move algorithm

排序运动后的第一组数据在排序后的第二组数据上的整体局部最优位置存在以下3种情况:在第二组数据的始端、在第二组数据的中间以及在第二组数据的末端．

2.2.1 始端位置最优匹配序列规划

当整体局部最优位置在第二组数据的始端时,处在第一组数据最右端的第一个数据向右移动一位,计算移动前后的单个方差值,若移动后的单个数据的方差值大于移动前的方差值,则将第一组数据右端未移动的邻接数据逐次递增的向右移动并检测方差值,直至数据移动,或者在所有数据进行移动方差检测后停止计算．若数据移动,检测当前移动数据和后面数据是否存在相邻连接关系,如果存在,则在没有移动到第二组数据末端的情况下,继续同时向右移动拼接后的数据,通过比较移动前后数据的方差值,确定数据的相对最优位置．继续通过迭代前进的方式移动第一组数据右端的从右向左的下一个数据,直到所有数据都进行了移动方差比较后停止,得到第一组数据在第二组数据上的最优匹配位置．数据移动的过程中,若移动后的方差大于移动前,则表示数据移动无效,移动数据退回前一个位置,算法流程如图2．

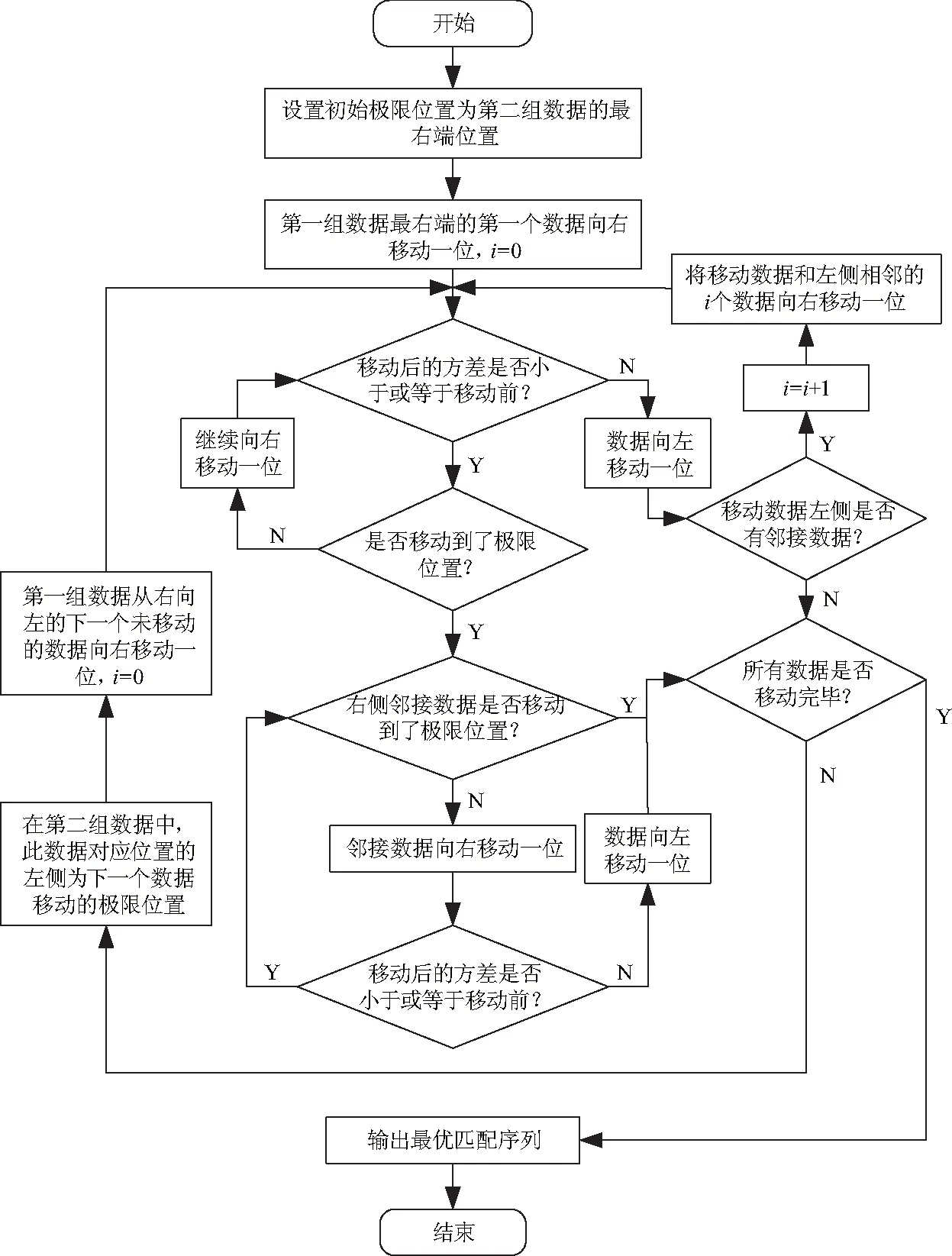
图2 始端位置最优匹配序列算法流程Fig.2 Flowchart of optimal matching sequence algorithm in the initial position

2.2.2 末端位置最优匹配序列规划

当整体局部最优位置在第二组数据的末端时,第一组数据在第二组数据匹配位置上的移动方向与在始端位置时正好相反,由数据的不断向右移动变为向左移动,算法以始端最优匹配序列规划运算方向的反方向进行数据的移动并比较移动前后的方差值,直至所有数据移动完毕,则得到第一组数据在第二组数据上的最优匹配位置．

2.2.3 中间位置最优匹配序列规划

整体局部最优位置在第二组数据的中间,即第一组数据在第二组数据的匹配位置上既能向右移动,也能向左移动，进行整体匹配最优序列的求解．数据在向右移动时的移动算法与始端位置最优匹配序列规划的算法一致,数据在向左移动时的移动算法与末端位置最优匹配序列规划算法一致．

数据在移动时,算法默认开始是选择将数据向右移动,当第一组所有数据都进行了向右移动的方差比较计算后,再将数据进行向左的移动计算,当第一组所有数据再次都进行了向左的移动方差比较计算后,算法结束,获得第一组数据在第二组数据上的整体最优匹配位置．

2.2.4 排序运动最优匹配结果论证

设匹配组件ε中有3个匹配件,零件尺寸分别为[a,b,c],另一组匹配组件η中也有6个匹配件,零件尺寸分别为[d,e,f,g,h,i],通过排序运动算法计算后的两组匹配数据的最优匹配结果如下:

根据定义1可以得到,在两组需要匹配零件数据的数量相同的情况下,整体的最优匹配序列是两组数据分别按照从小到大的顺序排列后的序列．也就是说,在两组需要匹配零件数据的数量相同的情况下,如果破坏了其中任何一组数据的从小到大顺序的条件后,整体的匹配序列则不是最优匹配序列．

同样在两组需要匹配零件数据的数量不相同的情况下,只要证明在破坏了第一组组数据的从小到大顺序的条件后,得不到更优匹配序列,则证明了排序运动算法所求得的匹配结果为最优匹配结果．

破坏第一组数据的从小到大的排序顺序,可以通过两种方式进行:① 交换已匹配位置的任意两个数据,比如交换按照从小到大顺序排列后的匹配组件ε中的数据a和数据c的位置;② 将某数据移动到其右侧数据的右侧或者其左侧数据的左侧,比如将按照从小到大顺序排列后的匹配组件ε中的数据a移动到数据c的右侧或者移动到数据b的左侧．方式①的证明过程和定义1的证明过程相同,结果为通过方式①无法得到更优匹配序列;证明方式②得不到更优匹配序列,也即是证明如下定义的正确性．

定义2:在获得的两组需要匹配的零件数据的数量不相同的情况下,在经过排序运动算法计算完成的第一组数据中的某个零件无法在其右侧零件的右侧或者左侧零件的左侧找到使整体匹配序列更优的位置．

假设定义2不成立,那么根据匹配组件ε和匹配组件η的匹配序列可得:

i2-g2<2ai-2iφ-2ag+2gφ

(4)

根据排序运动算法计算流程可得:

g2-i2<2ag-2gφ+2cd-2ad-2ci+2iφ

(5)

将式(4)和式(5)联立可得:

0<(d-i)(c-a)

(6)

因为d≤i,c≥a,所以式(6)不成立,也即是假设不成立,论证了定义2的正确性,同时也证明了通过排序运动算法计算所得到的匹配序列为最优匹配序列．

3 实例验证

根据上述的选配算法,如果两组匹配件的匹配数据的数量相同,只需进行一步排序运算,即可得到了最优的匹配序列,但是在产品的实际装配中,绝大多数情况下,两组匹配件的匹配数量是不相同的,因此文中主要针对两组不同数量的匹配数据进行验证．

通过企业车间的实际调研,以某型号船用柴油机的机架孔和气缸套的选配为验证对象,如图3,其中机架孔和气缸套的尺寸公差及配合精度如表1.

图3 机架孔和气缸套的匹配图Fig.3 Matching graphs of the frame hole and the cylinder sleeve表1 机架孔和气缸套的尺寸公差及装配精度Table 1 Accuracy of size tolerance and fitting of the frame hole and the cylinder sleeve