利用MATLAB合成音乐的函数模拟实现与比对
2018-08-06宋晓婷
宋晓婷
(山西建筑职业技术学院,山西 太原 030619)
MATLAB 是一种用于算法开发、符号运算、数据可视化、数据分析以及数值运算的高级技术计算语言和交互式环境.它的应用范围非常广,包括信号和图像处理、仿真、通讯、控制系统设计、测量和测试、建模和分析以及计算生物学等众多应用领域.它还被称为矩阵实验软件,可以进行矩阵运算、绘制函数和数据、实现算法、创建用户界面、连接其他编程语言的程序等.可以编写程序或调用存储函数解决数学问题,如初等数学的代数计算、三角函数求值;高等数学中的微积分计算;线性代数求解行列式、矩阵、线性方程组;微分方程求通解、特解;进行拉普拉斯变换,傅里叶级数的计算;还可以进行数据的筛检、对数据进行插值拟合、对未来数据的估测、给出误差分析等等多方面的应用,可以说是涉及面广,功能强大.
1 相关知识
先介绍一下乐理方面的相关知识,关于简谱和琴键的对应关系:基本音阶(是以全音、半音以及其他音程顺次排列的一串音)为C调大音阶,在钢琴上弹奏时全用白键,中央C是小字一组的do,也有D调、F调等.音阶分为“大音阶”和“小音阶”,即“大调式”和“靶〉魇”.大音阶由7个音组成,其中第3,4(即mi和fa)音之间和第7,8(即xi和高音do)音之间是半音程,其他音之间是全音程.小音阶第2,3(即re和mi)音之间和5,6(即so和la)音之间为半音程.这里不同的音高决定不同的声音频率,在软件中用不同的数值体现,起到调节音调的作用,经过数学公式调整可以模仿出原唱的效果.
2 曲谱的公式化
本文在MATLAB中表示乐音所用的抽样频率为fs=22 050 Hz,也就是所1 s钟内有22 050个点,根据抽样点数的多少就可表示出每个乐音持续时间的长短.给每个乐音定义存储对应的抽样点,再用sound函数播放即可.
选编歌曲《阿拉木汗》部分简谱
1=F 4/4
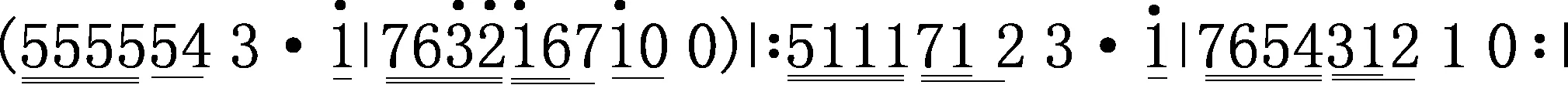
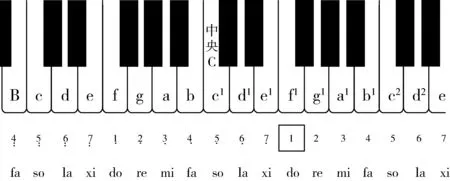
图1 琴键与简谱的对应
如图,4/4分母的4表示曲谱以四分音符为一拍,分子的4表示每小节4拍.利用MATLAB编写乐音需要区别每个音的节拍,确定其震动时间,数字下两横表示这个音是四分之一拍,4个这样的音为一拍;数字下一横表示这个音是二分之一拍,即半拍,两个这样的音为一拍;数字下方无横线表示这个音是一拍.数字之间的点代表半拍,这样可知每小节各个音节均为四拍.1=F表示小字一组的f1对应do的音,依次向前向后类推得表1.
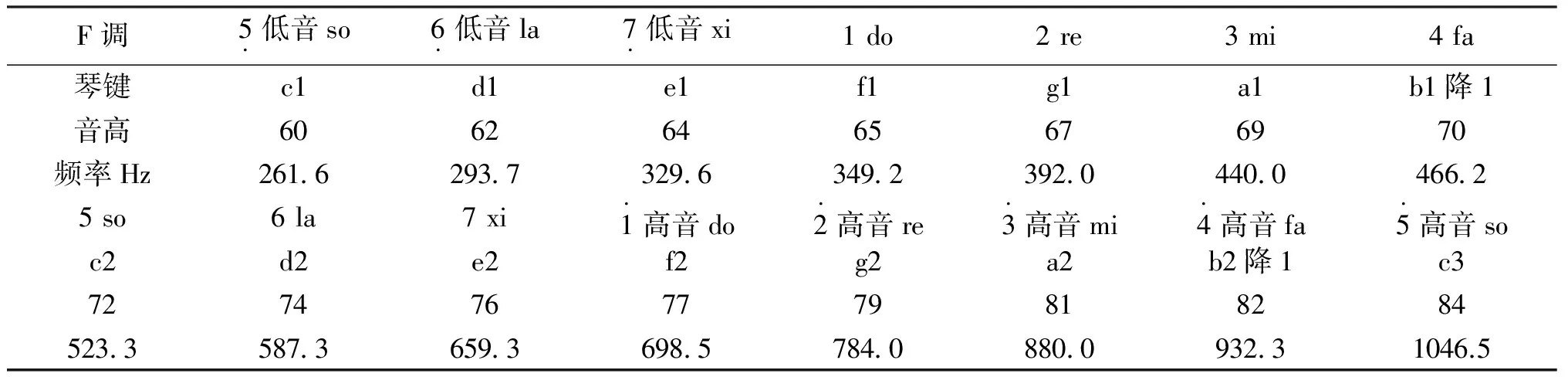
表1 常用琴键调高、音高、频率的关系
注:1)频率是由公式f=440×2(p-69)/12根据p的值用MATLAB计算得到的.
2)由于mi与fa、高音mi与fa均是半音程,b1降1 和b2降1表示该键左侧上方的黑键,音高只相差1.虽然低音xi与do的音高也只相差1,但在琴键上此处正好分别位于e1和f1的位置,它们正好也是半音程,所以无需降1.
3)表格只列出需要音高的数据,可根据实际向前或向后适当扩展.
3 函数模拟音乐效果比对
利用MATLAB的m文件编写音调和节拍程序如下,这里将低音so到高音so每个音调的一拍、半拍和四分之一拍给出定义,这个范围可以包括大多数歌曲的使用.若想保证所有曲谱的编写,只需将琴键上各个组别的音调类比给出定义即可.
编写m文件如下[1]:
3.1 有敲击声音,没空拍
function g=key(p,n,fs)
t=0∶1/fs∶4/n;
g=(sin(2*pi*fre(p)*t));
plot(g); %画出函数图像
function f=fre(p)
f=440*2^((p-69)/12).
3.2 有敲击声音,有空拍
由于每小节之间停顿的时间不同,要使歌曲听起来更逼真,就需要将此部分也考虑上.在前段程序中加入条件语句if和else,给空拍增加定义,且不能简单地定义为0,它的时间受节拍的控制,因此表达式与时间t有关,用0去乘之后,既有音调的无声体现,又涵盖相应的时间延续,控制每个乐音持续的时间要符合节拍,在歌曲播放出来时就会有空拍了.
function g=key(p,n,fs)
t=0∶1/fs∶4/n;
if p==-1 %定义空拍
g=0*(sin(2*pi*fre(p)*t));
else
g=(sin(2*pi*fre(p)*t));
end
plot(g)
function f=fre(p)
f=440*2^((p-69)/12);
3.3 指数函数对音乐的影响效果
消除敲击声音这是由于相位不连续产生了高频分量[2].这里可以类比实际中铁轨的弯道和直线衔接处,如果直接相连则会产生曲率的突变,导致火车侧翻或出轨,通常使用一个和轨道长度及曲率半径相关的三次函数来衔接,使曲率由0逐渐增大至弯道值再相连,这样就不会有危险.我们可以采用指数衰减的包络修正每个乐音,以保证在乐音的邻接处信号幅度为0.给每个乐音加一个指数衰减的包络,使声音有个减弱的过程,音调的清晰度增加,似有回声效果.
function g=key(p,n,fs)
t=0∶1/fs∶4/n;
tt=4/n∶-1/fs∶0;
g=(sin(2*pi*fre(p)*t)).*exp(tt);
plot(g);
function f=fre(p)
f=440*2^((p-69)/12).
3.4 傅里叶技术对音乐的影响效果
利用傅里叶技术在音乐中增加一些谐波分量[2],幅度要小于基波,不能掩盖住主体的音乐声调,需要加强声音的连贯程度.各个音结束时都有相对拉长的一个减弱过程,尾部音尤其明显.添加后声音比较浑厚,圆润饱满,在不会弹钢琴的情况下也能自己谱曲,享受一下自己的劳动果实.
function g=key(p,n,fs)
t=0∶1/fs∶4/n;
tt=4/n∶-1/fs∶0;
if p==-1
g=0*(sin(2*pi*fre(p)*t)+0.2*sin(6*pi*fre(p)*t)).*exp(tt);
else
g=(sin(2*pi*fre(p)*t)+0.2*sin(6*pi*fre(p)*t)).*exp(tt);
end
plot(g);
function f=fre(p)
f=440*2^((p-69)/12).
如果声音还比较尖锐,有些许刺耳,可能是选择的基波频率不合适,或者可以再加入另一种频率的谐波,变换他们的系数进行调试可达到良好的效果.
3.5 定义各音符频率、节拍、音调及空拍
fs=22 050; %每秒振动次数,即频率
t=0∶1/fs∶0.5; %每拍时间
c1-4=key(60,4,fs); %低音so一拍
c1-8=key(60,8,fs); %低音so半拍
c1-16=key(60,16,fs); %低音so四分之一拍
d1-4=key(62,4,fs); %低音la一拍
d1-8=key(62,8,fs); %低音la半拍
d1-16=key(62,16,fs); %低音la四分之一拍
e1-4=key(64,4,fs); %低音xi一拍
e1-8=key(64,8,fs); %低音xi半拍
e1-16=key(64,16,fs); %低音xi四分之一拍
f1-4=key(65,4,fs); %do一拍
f1-8=key(65,8,fs); %do半拍
f1-16=key(65,16,fs); %do四分之一拍
g1-4=key(67,4,fs); %re一拍
g1-8=key(67,8,fs); %re半拍
g1-16=key(67,16,fs); %re 四分之一拍
a1-83=key(69,8/3,fs); %mi 一拍半
a1-4=key(69,4,fs); %mi 一拍
a1-8=key(69,8,fs); %mi 半拍
a1-16=key(69,16,fs); %mi 四分之一拍
b1-4=key(70,4,fs); %fa 一拍
b1-8=key(70,8,fs); %fa 半拍
b1-16=key(70,16,fs); %fa 四分之一拍
c2-4=key(72,4,fs); %so 一拍
c2-8=key(72,8,fs); %so 半拍
c2-16=key(72,16,fs); %so四分之一拍
d2-4=key(74,4,fs); % la一拍
d2-8=key(74,8,fs); % la半拍
d2-16=key(74,16,fs); %la四分之一拍
e2-4=key(76,4,fs); %xi一拍
e2-8=key(76,8,fs); %xi半拍
e2-16=key(76,16,fs); %xi四分之一拍
f2-4=key(77,4,fs); %高音do一拍
f2-8=key(77,8,fs); %高音do半拍
f2-16=key(77,16,fs); %高音do四分之一拍
g2-4=key(79,4,fs); %高音re一拍
g2-8=key(79,8,fs); %高音re半拍
g2-16=key(79,16,fs); %高音re四分之一拍
a2-83=key(81,8/3,fs); %高音mi一拍半
a2-4=key(81,4,fs); %高音mi一拍
a2-8=key(81,8,fs); %高音mi半拍
a2-16=key(81,16,fs); %高音mi四分之一拍
b2-4=key(82,4,fs); %高音fa一拍
b2-8=key(82,8,fs); %高音fa半拍
b2-16=key(82,16,fs); %高音fa四分之一拍
c3-4=key(84,4,fs); %高音so一拍
c3-8=key(84,8,fs); %高音so半拍
c3-16=key(84,16,fs); %高音so四分之一拍
k-4=key (-1,4,fs); %空一拍
k-8=key (-1,8,fs); %空半拍
k-16=key (-1,16,fs); %空四分之一拍
3.6 合成音乐
part1=[c2-16 c2-16 c2-16 c2-16 c2-8 b1-8 a1-83 f2-8];%第十一部分重复
part2=[e2-16 d2-16 a2-16 g2-16 f2-16 d2-16 e2-8 f2-8 k-8 k-4];
part3=[c1-16 f1-16 f1-16 f1-16 e1-16 f1-16 g1-8 a1-83 f2-8];
part4=[e2-16 d2-16 c2-16 b1-16 a1-16 f1-16 g1-8 f1-4 k-4];%第十部分重复
part5=[k-8 c2-16 c2-16 c2-8 d2-8 f2-16 f2-16 f2-8 k-4];
part6=[k-4 f2-16 f2-16 f2-8 d2-16 f2-16 d2-16 c2-16 c2-8 k-4];
part7=[k-8 f2-16 f2-16 f2-8 f2-8 d2-16 f2-16 d2-16 c2-16 c2-8 a1-8];
part8=[k-8 c2-16 c2-16 a1-8 a1-8 g1-16 g1-16 a1-8 k-4];
part9=[c1-16 f1-16 f1-16 f1-16 f1-8 g1-8 a1-83 f2-8];
part12=[e2-16 d2-16 a2-16 g2-16 f2-16 d2-16 e2-8 f2-4 k-4];
part13=[c2-16 c2-16 c2-16 c2-16 c2-8 b1-8 a2-83 f2-8];
part14=[e2-16 f2-16 g2-16 a2-16 g2-16 d2-16 e2-8 f2-4 k-4];
line1=[part3 part4 part3 part4 part5 part6 part7 part8 part9 part4];
line2=[part1 part12];
line3=[part13 part14];
legend=[line1 line2 line3];
sound(legend,fs)
4 频谱分析
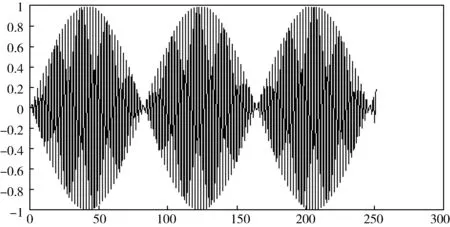
图2 fs=1000波形振动图像
频率可适当调整,图2是当fs=1 000临界值时的波形振动图像.频率越大图像越密,声音越流畅,更接近原声,通常取8 000,14 400等;频率取值越小图像分割越粗糙,声音不流畅,间隔明显,听起来与原声相差甚远.如fs=200则出错,低于1 000为无效的样本率.利用clear sound命令可以随时停止音乐播放.
5 总结
本设计用MATLAB构建的音乐合成程序简单易懂,可灵活多变,成功地实现了音乐的简单合成、音乐的降噪处理以及音乐的加傅里叶变换谐波处理,使得生涩的音乐逐步调整为优美动听的声音.利用软件的强大功能实时给出相应频率分析图像,更清晰地显示曲子的频率与曲调的关系.我们可以充分发挥自己的创新能力,通过选取不同的加工算法,对音乐分别处理,抑制噪声,改善音乐质量,便于人们欣赏品鉴.
