具有时滞和基于比率的捕食系统的正周期解

安 莹

(晋中师范高等专科学校,山西 晋中 030600)

0 引言

种群的持续生存是生态数学中捕食系统理论的一个重要而普遍的问题，对于标准的Lotka-Volterra型捕食系统一般均假设捕食者种群的平均捕食率只依赖于食饵种群的密度.近年来，越来越多的生物学证据表明，当捕食者不得不寻找食物时，一个更符合实际情况且更一般的捕食模型应基于比率依赖理论[1-3]，也就是说捕食者种群的平均捕食率是食饵种群密度与捕食者种群密度之比的函数；另一方面，在种群间的相互作用中时滞是不可避免的，近年来已有大量的文献讨论了时滞对生物种群的渐进性态的影响；同时，种群在两斑块间的扩散对种群持续生存也有影响.对于扩散模型已有大量的研究.

本文是在文献[4]的基础上，讨论了具有时滞和基于比率的非自治捕食系统.模型如下：

(1)

其中x1，x2分别表示食饵x1，x2在t时刻在斑块I和II中的密度，x3表示捕食者种群在t时刻的密度.X1和X2是X3的食饵，且在斑块I和II中扩散.a1(t)，a2(t)，a3(t)，a11(t)，a22(t)，a13(t)，a23(t)，a31(t)，a32(t)，m(t)，D1(t)，D2(t)均为连续的严格正的ω-周期函数.

本文的目的是利用Mawhin的拓展定理[5]，来研究系统(1)的正周期解的存在性.

1 基础知识

设X，Z是两个Banach空间，考虑算子方程Lx=λNx，λ∈[0，1]，其中L：

DomL∩X→Z为线性算子，定义两个投影算子P：X∩DomL→X和Q∶Z→X/ImL，且有ImP=KerL，ImL=KerQ.下面我们将用到Mawhin的如下结果：

引理1设X，Z是两个Banach空间，L是指标为零的Fredholm映射，

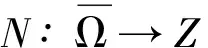
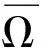
i)Lx≠λNx，∀x∈∂Ω∩DomL，λ∈(0，1)；

ii)QNx≠0，∀x∈KerL∩∂Ω；

iii)deg{QNx，Ω∩KerL，0}≠0.

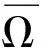
为了便于证明，对连续的正ω-周期函数g(t)，给出如下定义：

2 正周期解的存在性

定理如果下列条件成立：

i)Di(t)

那么系统(1)至少存在一个正ω-周期解.

定理的证明过程类似于参考文献[4]，有兴趣的可以看看.