可有效更新的低存储开销公共可验证数据库方案
2018-08-06吴淇毓周福才李宇溪
吴淇毓 周福才 王 强 李宇溪
(东北大学软件学院 沈阳 110169) (kathywuqy@gmail.com)
随着互联网应用的迅速发展,数据量和用户数快速增长,使得客户对数据的存储、管理与维护变得更具挑战性.越来越多资源受限的客户将大型数据库外包到专业数据库服务提供商(database service provider, DSP)[1],并希望得到安全保证,使其可以从DSP查询或更新数据记录,且可以检测并验证所查询数据的完整性.效率方面,要求客户的计算开销独立于数据库的大小;安全性方面,要求客户能够检测出数据是否被篡改.
近年来,研究者们提出了一系列方案来解决上述问题.一种最直接的方法是利用数字签名[2-3]来实现.然而,该方案需要在本地记录每一次更新,存储开销较大,不支持大量的数据更新.为了减少签名的次数,基于认证数据结构[4-11]的方法被提出,可以利用验证树对其根结点签名,从而减小构造验证信息的计算量,或者基于可翻转的布隆过滤器[12],有效避免数据更新操作时额外的计算开销,但布隆过滤器存在误算率.此外,为了减少服务器与用户之间交互的通信量,研究者们还提出了基于动态累加器[13-15]的方法,可以有效验证查询结果并对数据进行更新.然而上述2种方法或依赖于非常量大小(non-constant size)的困难假设(如q-Strong DH假设),或需要完成生成素数等计算负担较大的操作.
Benabbas等人[16]首次提出了一个支持有效查询和更新的可验证数据库(verifiable database,VDB)方案.他们的方案依赖于合数阶双线性群(bilinear groups of composite order)常量大小的困难假设,然而不支持公共可验证,即只有数据库的拥有者才可以对数据查询结果进行验证.
为了解决该问题,Catalano等人[17]将向量承诺方案应用于可验证数据库,依赖于标准常量大小假设,提出了一种公共可验证数据库方案.但该方案中公共参数的大小依赖于数据库大小,因此客户在预处理阶段的计算开销和存储开销会随着数据库增大呈幂增长.此外,该方案中的更新算法只支持修改数据,不支持添加或删除数据.
基于文献[17],Miao等人[18]利用分层承诺的思想首次提出了一个支持修改、删除和添加数据的可验证数据库方案,并满足标准计算性Diffie-Hellman假设.然而,客户进行更新操作的计算负担随着分层数量的增加而增大,并且该方案同文献[17]一样,没有解决客户的存储开销问题.
本文在上述文献的基础上对可验证数据库展开研究,以降低客户的存储负担、支持对数据的添加和删除操作为目标,提出一个可有效更新的低存储开销公共可验证数据库模型,并对其正确性和安全性给出了形式化定义,构造了一个具体的可有效更新的低存储开销公共可验证数据库方案(publicly verifiable databases scheme with efficient updates and low storage overhead, PVDB-EL).方案支持客户对外包数据库中数据查询结果的公共可验证,与已有方案相比,该方案基于素数阶双线性群,提高了计算效率;同时,在初始化阶段构造了独立于数据库大小的公共参数,减小了客户的存储开销;此外,该方案支持对外包数据的修改、添加及删除操作.通过对其计算效率的分析,方案满足客户查询、更新和验证等操作开销独立于数据库大小,保证了效率.方案的安全性可以规约为平方计算性Diffie-Hellman(square computational Diffie-Hellman, Square-CDH)问题假设.
1 相关知识
1.1 双线性映射
设G和GT为p阶循环群,g为G的生成元.定义2个群上的双线性映射为e:G×G→GT,且满足以下性质:
1) 双线性.e(ga,gb)=e(g,g)ab,对所有的a,b∈均成立.
2) 非退化性.e(g,g)≠1.
3) 可计算性.存在有效算法来计算t=e(g,g).
1.2 平方计算性Diffie-Hellman问题及困难性假设
定义1. Square-CDH问题[19].设λ∈为安全参数,G为素数p阶群,g是G的生成元,e:G×G→GT为双线性映射,给定g,gα∈G,其中p,计算gα2.概率多项式时间算法A计算出G上的Square-CDH问题的概率定义为Pr[A(g,ga)=ga2].
定义2. Square-CDH困难问题假设.如果不存在一个概率多项式时间算法能够以不可忽略的概率ε来计算出G上的Square-CDH问题,即Pr[A(g,ga)=ga2]≤neg(λ),其中neg(λ)为可忽略函数,则称群G上的Square-CDH问题是困难的.
2 PVDB-EL的形式化定义及安全模型
PVDB-EL方案的应用场景包括数据拥有者、客户和DSP这3个实体.如图1所示,数据拥有者在初始化阶段对数据库进行编码并生成公钥和私钥,之后将数据库外包到DSP进行存储和管理.其中,公钥包含用于验证查询阶段服务器返回的证据的公共参数,私钥用于对外包数据库进行更新.只有数据拥有者可以对数据库进行更新;该方案支持公共可验证,多个客户都可以对DSP中的外包数据库进行查询;由于DSP是不可信的,可能会对数据库的内容进行篡改,因此在返回查询结果的同时,DSP还将返回相应证据来证明客户端所查询数据的完整性,数据拥有者和客户可以利用获得的公钥进行验证.
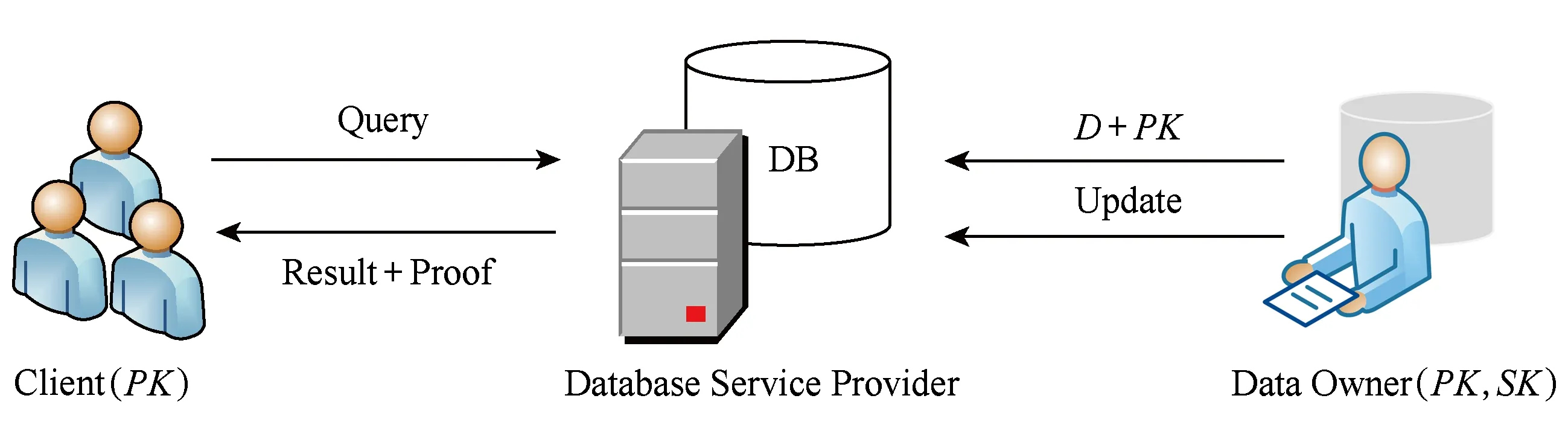
Fig. 1 The application scenario of PVDB-EL图1 PVDB-EL方案应用场景
2.1 PVDB-EL的形式化定义
该方案由5个概率多项式时间算法组成:初始化算法、数据查询算法、公共可验证算法、数据更新算法、数据库更新算法.下面分别对其进行具体的描述.
1) Setup(1λ,D)→(PK,SK,S)初始化算法.输入安全参数λ和数据库D,数据拥有者执行初始化算法,对数据库编码得到S并发送给服务器.私钥SK由客户私密保存,公钥PK被分发给所有想对数据库进行验证的客户.
2) Query(PK,S,i)→(vi,Pi)数据查询算法.客户将待查询数据的位置i作为输入,服务器执行数据查询算法并返回i处的数据vi及证据Pi.
3) Verify(PK,i,vi,Pi)→{0,1}公共可验证算法.客户对服务器返回的查询结果进行验证.如果vi=D(i)验证正确,则算法接受结果vi并输出1,反之输出0.其中1代表验证结果正确,0代表验证结果错误.
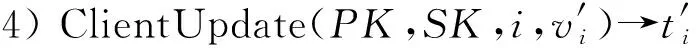
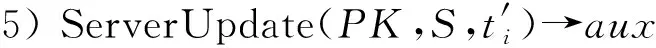
2.2 PVDB-EL的正确性及安全性定义
2.2.1 正确性
设λ是初始化选定的安全参数,D是数据库,定义算法check为多项式时间算法,其以数据库中位置i、查询结果vi、数据库D为输入,当D中位置i处数据确为vi时,返回accept,否则返回reject,即{accept,reject}←check(i,vi,D(i)).
对于任何i=0,1,…,poly(λ),PVDB-EL方案是正确的,则要求各算法正确执行后,算法查询结果满足:
其中,neg(λ)为可忽略函数.
2.2.2 安全性
假设所有的外包服务器均为不可信,即外包服务器会试图获取额外的信息,从而可能会对数据库的内容进行篡改.在PVDB-EL的安全模型中,敌手能够查询外包数据库中的任意数据,并针对数据库的某一位置,试图伪造一个与数据拥有者的初始数据不相等的数据返回给用户,且能够通过用户的验证.
设λ是初始化选定的安全参数,D是数据库,下面通过敌手A和挑战者C的安全游戏Π给出安全性定义.
安全游戏Π:
定义敌手A,对于选定变量,它试图通过以下阶段来伪造一个结果通过验证.
Setup: C执行Setup算法,并把公钥PK以及数据库编码S发送给A.
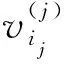
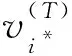
定义3. 在上述安全游戏过程中,如果敌手A伪造成功的概率满足:
其中neg(λ)为可忽略函数,则称PVDB-EL是安全的,满足不可伪造性.
3 PVDB-EL方案的描述
3.1 算法详细设计
在本节中,对PVDB-EL方案中的5个多项式时间算法即初始化算法、数据查询算法、公共可验证算法、数据更新算法、数据库更新算法进行详细的设计和描述.
1) 初始化算法Setup(1λ,D)→(PK,SK,S)
该算法用于生成密钥以及对数据库进行编码.算法的主要步骤如下:
①λ∈为安全参数,数据库D={(i,vi)}(1≤i≤n,n=poly(λ)),其中i∈(q,n]时vi=0(q∈[1,n]).数据拥有者将数据库外包到服务器.首先生成一个λ位的素数p,再生成p阶循环群G和GT,及双线性映射函数e.
② 随机选择种子k并利用伪随机函数Fk(i)=zi→p生成zi,取G中生成元g,计算∀i∈[1,n]),利用si计算
③ 随机选择参数α→p,并计算pk=gα.
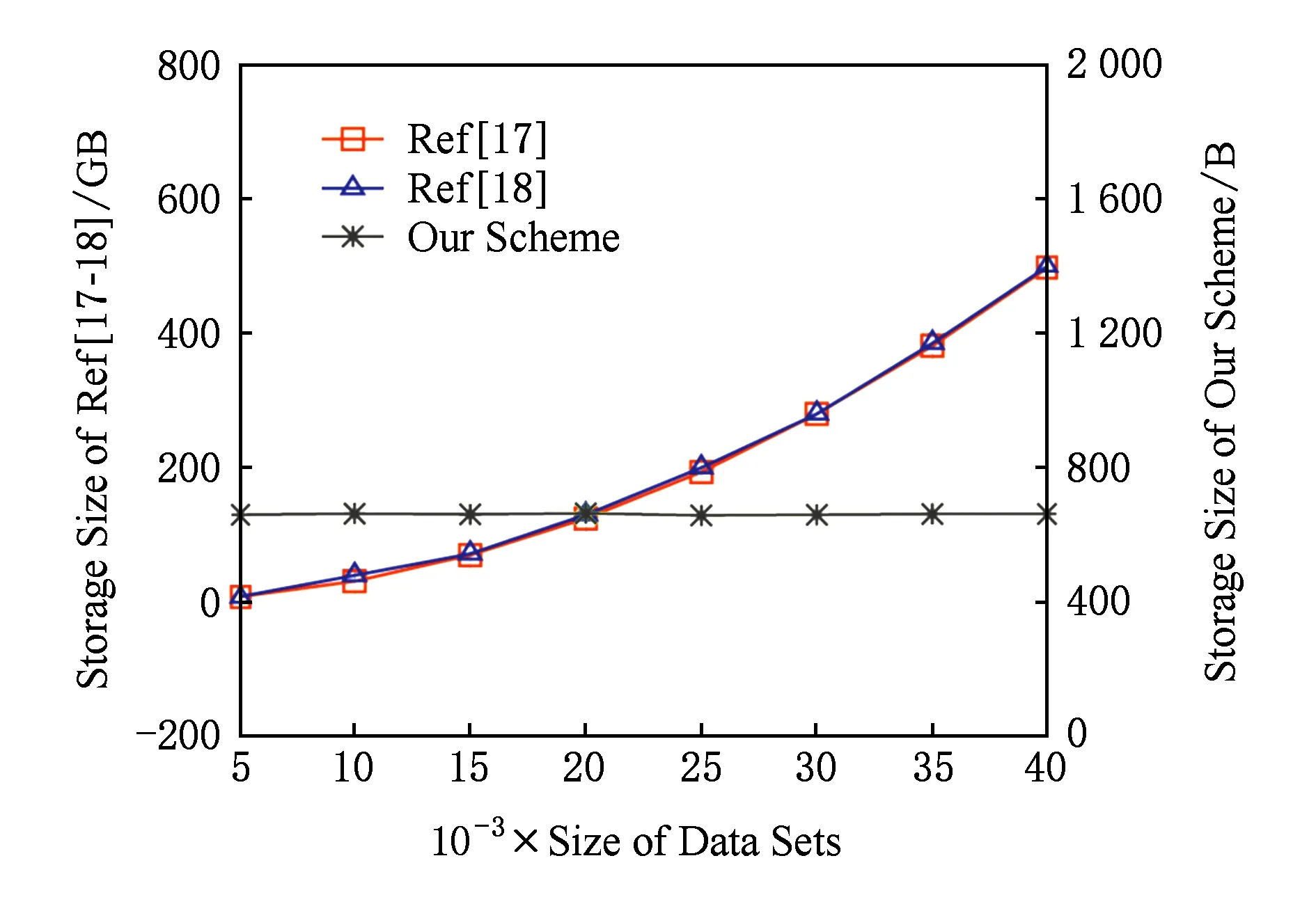
④ 令辅助信息aux包括数据库内存储的数据,则aux=(v1,v2,…,vn),其中vi=0(q ⑤ 输出公钥PK=(pp,C,pk),私钥SK=α,对数据库D进行编码得到S=(pp,aux,D). 2) 数据查询算法Query(PK,S,i)→(vi,Pi) 该算法用于返回客户查询的数据及用于验证该数据完整性的证据.算法的主要步骤如下: ① 以位置i为输入,根据vi=D(i),服务器返回vi的值. 3) 公共可验证算法Verify(PK,i,vi,Pi)→{0,1} 该算法利用服务器返回的证据,验证所查询数据是否正确.算法的主要步骤如下: ① 利用公钥PK、位置i、服务器返回的数据vi、证据Pi及双线性映射e来验证等式 (1) 是否成立. ② 如果式(1)成立,则该算法接受结果vi,输出1;反之拒绝结果vi并且输出0. 该算法用于返回更新后的公钥及相关更新信息.算法的主要步骤如下: ③ 得到更新后的公钥PK′=(pp,C′,pk). 该算法用于更新数据库记录.算法的主要步骤如下: 本节将通过对数据拥有者、客户和服务器这3个实体间的交互对方案的详细设计进行描述. 1) 在初始化阶段,数据拥有者首先选定待外包的数据库,然后运行算法Setup(1λ,D)为系统生成密钥以及数据库的编码.对于已选定的数据库,数据拥有者将通过编码的方式来保证数据库内数据的机密性. 2) 数据拥有者将编码后的数据库外包到服务器,将私钥自己留存,把公钥发送给客户和服务器. 3) 当客户(包括数据拥有者在内)想要对服务器中的数据库进行查询时,运行Query(PK,S,i)算法来查询位置i处对应的数据.算法返回数据vi及用于验证该数据完整性的证据给客户. 4) 客户在接收到数据及证据后,将利用Verify(PK,i,vi,Pi)算法对数据的完整性进行验证.若验证通过,则接受vi,反之拒绝vi. 定理1. 如果方案步骤都是正确执行,产生的结果都是按照正确步骤执行得到、没有被恶意篡改的,则客户端将以极大概率接受结果,即客户端执行验证算法Verify(PK,i,vi,Pi)→1. 因此Verify(PK,i,vi,Pi)→1,定理1成立,方案满足正确性. 证毕. 定理2. 如果存在一个敌手A可以在不可忽略的概率多项式时间内赢得安全游戏Π,那么就存在一个有效算法B能够以不可忽略的概率解决Square-CDH问题. 证明. 为了证明针对数据库内的同一位置,敌手A不能返回给客户2个不同的数据,接下来先证明如何构建一个有效的算法B来使A能够以不可忽略的概率解决Square-CDH问题. 令si*=gα,则化简得到: 由此可以计算出gα2,即B算法可以在概率多项式的时间内解决Square-CDH问题. 又由于Square-CDH问题是难解的,因此定理2不成立,即不存在概率多项式时间内的敌手A能够以不可忽略的概率赢得安全游戏.因此方案是安全的. 证毕. 本节将本文所提方案与文献[16-18]进行对比.功能方面主要比较了方案是否支持公共可验证、是否支持数据插入及删除操作、双线性群的类型、计算性假设的类型等;性能方面主要比较了客户的存储开销复杂度及算法的计算代价,算法包括服务器的查询算法、客户的验证算法以及更新算法.比较结果如表1所示. 从表1可以看出,功能方面,文献[16]不能支持公共可验证,且基于合数阶双线性群,计算效率较低;文献[17]虽然支持了公共可验证,但却不支持数据的插入和删除操作;本文所提方案基于素数阶双线性群,支持对查询结果的公共可验证,并支持对外包数据的插入和删除操作. 性能方面,定义n是外包数据库的大小,M是G上乘法的计算代价,E是G上指数的计算代价,I是G上求逆的计算代价,P是双线性对的计算代价,L是当前数据库中的总层数.文献[17-18]中客户的存储开销均为O(n2),会随着数据库的增大呈幂增长,而本文所提方案构造了常量大小的公共参数,减小了客户的存储负担;本方案查询算法的计算代价同文献[17-18]一样,优于文献[16];本方案验证算法的计算代价虽略逊于文献[16-17],却优于文献[18];客户更新算法的计算代价与文献[17]相同,优于文献[16,18]. 综合以上对比,本文所提方案在功能及性能方面整体上优于对比方案. Table 1 Comparison Among Four Schemes表1 方案比较 由于本方案在功能方面优于文献[16],因此在本节中通过相关实验,分别对本方案及文献[17-18]中方案的存储开销、验证效率以及更新效率进行测试、对比与分析.实验采用JPBC库实现双线性群的初始化,对大小为[5 000,40 000]的数据集分别进行了测试,测试的每一个数据结果均是10次运行结果的平均值,其中排除了明显错误的数据.运行实验程序的计算机配有Intel®CoreTMi3-3240 3.40 GHz主频的处理器和8 GB内存. 1) 比较本方案与文献[17-18]中客户的存储开销,客户需要存储PK用于之后的查询及验证操作.实验结果如图2所示,由于数量级相差较大,图2中左面的纵坐标表示对比文献中客户的存储开销,右面的纵坐标表示本方案的存储开销,横坐标为外包数据库中的数据集大小.实验结果表明,本方案的存储开销为常量,独立于数据集大小,并且远远小于文献[17-18]中测试结果的数量级.它们的方案在数据集大小为5 000时的存储开销已达到约7 GB. Fig. 2 Comparison of storage size图2 存储开销对比 这是因为在对比文献中,初始化阶段的公共参数pp的大小为O(n2),当数据库增大时,客户查询更新和验证等操作开销将会变得很大.本方案中客户在公共参数pp中不需要存储所有的参数si,只需要存储g以及伪随机函数的种子k,存储开销为O(1).利用这2个参数,可以计算出C,最终得到公钥.在验证服务器返回的数据时,客户只需要利用g和k生成特定的si来验证返回结果是否正确.本方案公共参数pp的大小为常量,减小了客户的存储负担,并使得客户验证和更新等操作开销均独立于数据库大小. 2) 比较本方案与文献[17-18]中验证操作的执行时间.实验结果如图3所示,图3中纵坐标为操作的执行时间,横坐标为外包数据库中的数据集大小.实验结果表明,本方案中验证操作的时间开销高于文献[17]、低于文献[18],且验证开销为常量.这是因为本方案比文献[17]多进行了一次双线性配对操作,文献[18]比本方案多进行了一次配对操作.由于本方案独立于数据集大小,因此可以对外包数据库的查询结果进行有效验证. Fig. 3 Comparison of running time for Verify图3 验证操作执行时间对比 3) 比较本方案与文献[17-18]中客户更新操作的执行时间.实验结果如图4所示,其中文献[17]相关数据以层数L=1为例,图4中纵坐标为操作的执行时间,横坐标为外包数据库中的数据集大小.实验结果表明,本方案中更新操作的时间开销与文献[17]一致,明显优于文献[18],且更新操作的时间开销为常量.这是因为文献[18]比本方案及文献[17]多进行了1次G上乘法运算及L次G上指数运算.由于本方案独立于数据集大小,因此可以对外包数据库的查询结果进行有效更新. Fig. 4 Comparison of running time for ClientUpdate图4 更新操作执行时间对比 4) 比较本方案中初始化操作、验证操作及更新操作的执行时间.实验结果如图5所示,由于数量级相差较大,图5中左面的纵坐标表示验证操作及更新操作的执行时间,右面的纵坐标表示初始化操作的执行时间,横坐标为外包数据库中的数据集大小.实验结果表明,数据进行初始化操作的执行时间在数据集大小为5 000时已约为4 ks.而验证操作和更新操作的执行时间远远小于对数据进行初始化操作的执行时间,满足外包数据库方案的要求,有利于外包数据库的公共可验证,并且验证及更新操作的时间开销为常量,独立于数据集大小,可以对外包数据库进行有效验证及更新. Fig. 5 Comparison for Setup, Verify and ClientUpdate图5 初始化、验证、更新操作执行时间对比 以上4个实验的结果表明,可有效更新的低存储开销公共可验证数据库方案在客户的存储开销、验证查询结果的执行时间以及对数据进行更新操作的执行时间上都有很大的优势,并且数据库中数据集越大,优势越明显.其原因是:本方案中客户在初始化阶段中的公共参数pp中只存储了g以及伪随机函数的种子k这2个常量参数,在验证和更新操作时,客户只需要利用该常量的公共参数来进行计算,由于公共参数的大小为常量,减小了客户的存储负担,并使得客户验证和更新等操作开销均独立于数据库大小. 本文深入系统地研究了国内外关于外包数据库查询结果完整性的相关方案,总结各方案的优缺点,并进一步研究了可验证数据库相关理论,提出了一个可有效更新的低存储开销公共可验证数据库方案.文中给出了方案的形式化定义以及证据的生成、查询结果的验证和数据的更新方法,同时给出了正确性及安全性分析与证明.与已有方案相比,该方案基于素数阶双线性群,提高了计算效率,并在初始化阶段构造了独立于数据库大小的公共参数,减小了客户的存储开销.同时,方案验证无需私钥参与,从而实现了公共可验证.该方案不仅支持对数据进行修改,还支持对数据的插入及删除操作.性能分析表明方案满足客户查询、更新和验证等操作开销独立于数据库大小,因此具有验证速度快、更新效率高的优势.该方案对于外包数据库查询结果完整性问题具有一定理论意义和实际应用价值. WuQiyu, born in 1994. Received her master degree from the Software College, Northeastern University in July 2018. PhD candidate. Her main research interests include verifiable computation and network security. ZhouFucai, born in 1964. PhD, professor and PhD supervisor. Senior member of CCF. His main research interests include cryptography and network security, trusted computing, and critical technology in electronic commerence. WangQiang, born in 1991. PhD candidate. His main research interests include verifiable computation and outsourced database. LiYuxi, born in 1990. PhD candidate. Her main research interests include secure cloud storage and searchable encryption.
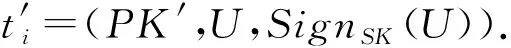
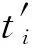
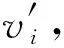
3.2 方案详细设计
4 正确性及安全性证明
4.1 正确性证明
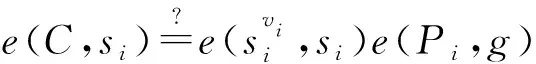
4.2 安全性证明
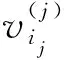
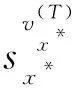
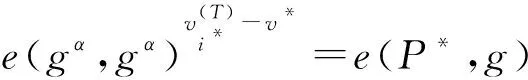
5 性能分析
5.1 方案对比
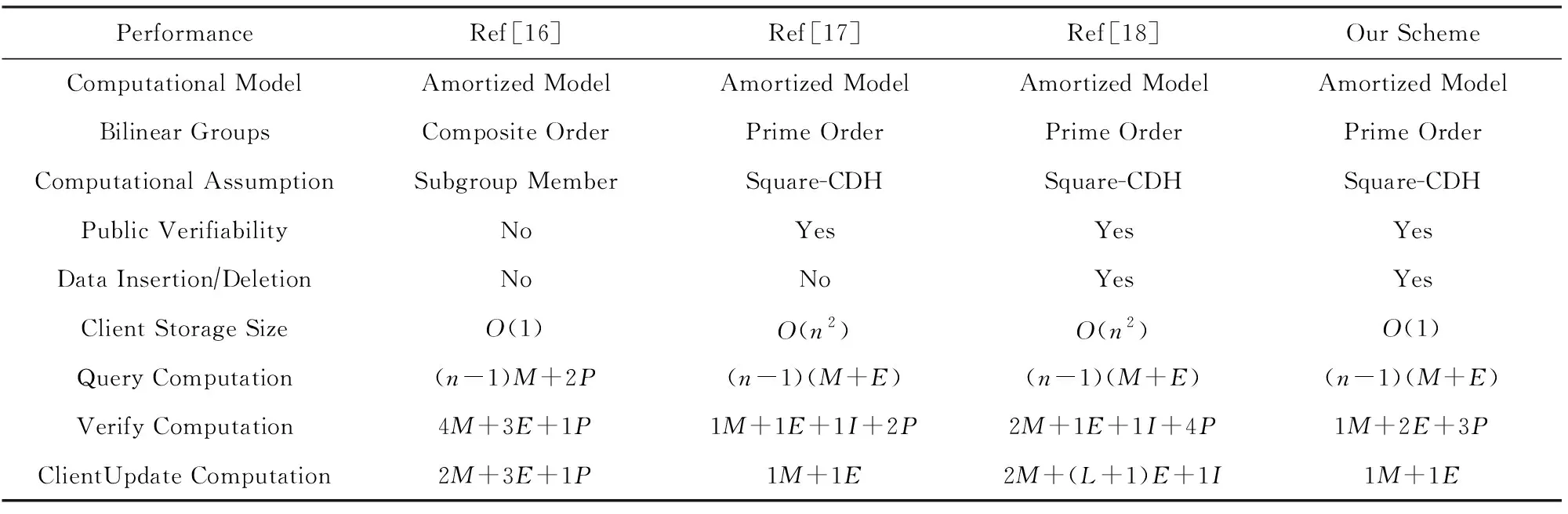
5.2 效率分析
6 结 论




