带高耗能黏弹性阻尼器腋撑RC框架结构抗震性能
2018-08-03董尧荣徐赵东徐业守
董尧荣 徐赵东 葛 腾 徐业守
(东南大学混凝土及预应力混凝土结构教育部重点实验室, 南京 210096)
震害调查表明,钢筋混凝土(RC)框架结构大多是由于框架梁柱节点的破坏导致结构失效或倒塌[1].而现行的以延性设计为目标的抗震规范难以满足“强节点弱构件”的要求,设计困难.文献[2]提出了在梁底部加设腋撑以提高受损RC框架节点的抗震性能,并对4个全尺寸样本进行了静力及动力试验,验证了该方案的有效性.文献[3]对一个五层带屈曲约束腋撑进行了动力时程分析,分析结果表明采用该方法设计的带耗能腋撑钢框架内力分布均匀,所有腋撑为塑性变形耗散地震能量.文献[4]对抗震设计欠佳的既有RC框架结构提出一种加设腋撑的方案来避免节点区发生脆性剪切破坏,并通过低周反复抗震性能实验验证了该方案的有效性.文献[5]研究了一种新型的带腋撑RC框架结构力学性能,结果表明该新型结构梁端、柱端及节点区受力性能良好,可以保证结构具有良好的承载能力和变形能力.文献[6]进行了带黏滞阻尼器腋撑钢筋混凝土框架结构抗震性能试验研究,结果表明该结构能有效地保护梁柱节点,提高了钢筋混凝土框架的抗震性能.
课题组研发了一种高耗能黏弹性阻尼器,在大、小位移幅值下均表现出良好的耗能性能且能提供一定刚度,同时具有构造简单、制作方便、价格低廉等特点.为避免或减缓框架结构出现“弱节点”的破坏模式,本文提出了一种能保证建筑面积与净空高度的带高耗能黏弹性阻尼器腋撑的新型框架结构.对带高耗能黏弹性阻尼器腋撑RC框架和普通RC框架进行了宽频大幅值正弦位移的激励荷载作用下的抗震性能对比分析,以研究该新型结构的抗震性能.
1 有限元模型的建立及验证
ABAQUS有限元软件可模拟三维空间实体框架结构在动静载下的高度非线性响应,且具有较高的数值稳定性和精确性[7].本节采用文献[6]的试验结果对本文建立的有限元模型进行验证,为后继的有限元分析建立正确可信的数值模拟平台.
1.1 有限元模型的建立
采用ABAQUS对文献[6]中的试件RCF(普通钢筋混凝土框架)进行模拟,以及对试件VEDF(带高耗能黏弹性阻尼器钢筋混凝土框架)进行模拟.除高耗能黏弹性阻尼器腋撑外,试件RCF参数与试件VEDF相同,图1仅给出试件VEDF的尺寸及构造详图.
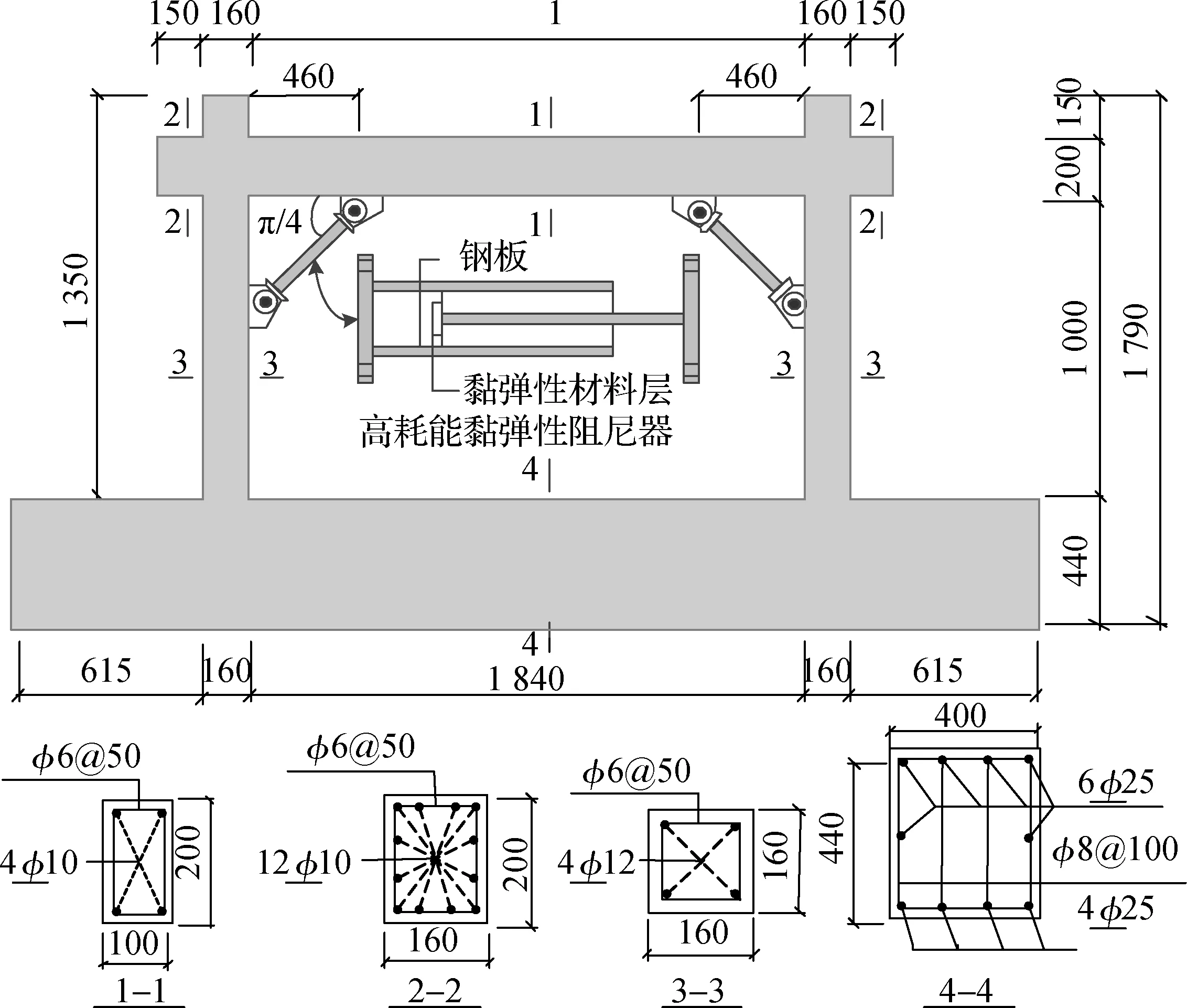
图1 试件几何尺寸、配筋以及阻尼器布置(单位:mm)
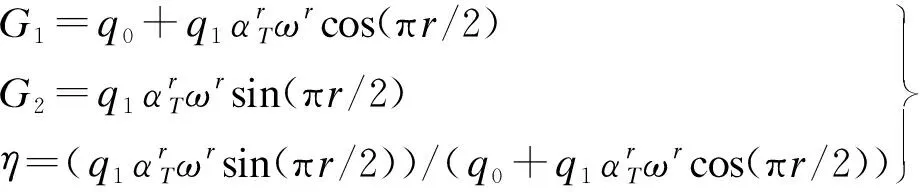
(1)
式中,q0为线性弹簧的弹性模量;q1为黏壶的黏性系数;r为分数导数的阶次;αT为温度转换系数;ω为频率;G1为储能模量;G2为耗能模量;η为耗能因子.
高耗能黏弹性阻尼器的有效刚度Ke和有效阻尼Ce通过下式求得[10]:
Ke=nvG1Av/hv
(2)
Ce=nvηG1Av/(ωhv)=ηKe/(2πf)
(3)
式中,nv为黏弹性材料层的数量;Av和hv分别为黏弹性材料层的剪切面积和厚度;f为加载频率.
本文选用与文献[9]同型号同参数的高耗能黏弹性阻尼器,黏弹性材料层的数量为2层,黏弹性材料层的剪切面积Av=0.02 m2,厚度hv=7 mm.温度取常温20 ℃.
由以上方法建立的有限元模型如图2所示.模拟时首先在混凝土柱顶均施加80 kN(轴压比为0.1) 的竖向荷载.由于高耗能黏弹性阻尼器为速度相关型耗能装置,须采用动力加载的方法才能体现其真实情况,故在梁端施加水平正弦位移的激励荷载ud=u0sinωt,ω=2πf,加载频率f=0.05~3 Hz,以位移幅值控制加载.
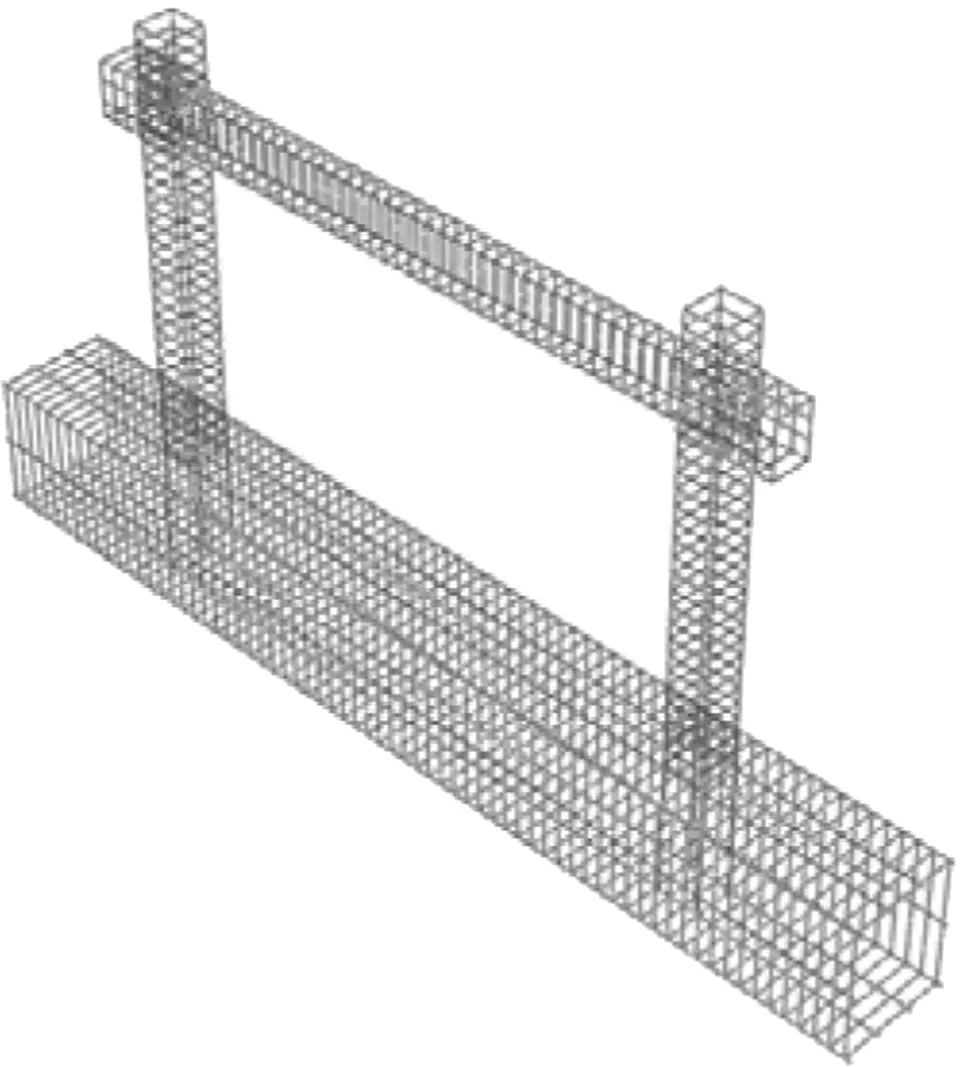
(a) 钢筋骨架
1.2 有限元与试验结果对比
试件RCF(与试验同工况)有限元分析与试验的框架顶点位移滞回曲线与骨架曲线对比如图3所示.由图可知,两者的滞回曲线和骨架曲线基本吻合,验证了本文建立的有限元模型的有效性和可靠性.故本文有限元模型能较好地模拟正弦位移的激励荷载作用下RC框架结构的滞回特性,有限元模型可用于后续分析.
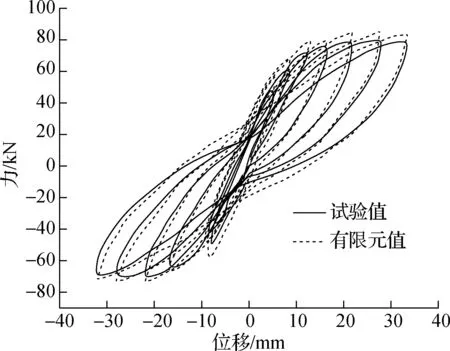
(a) 滞回曲线
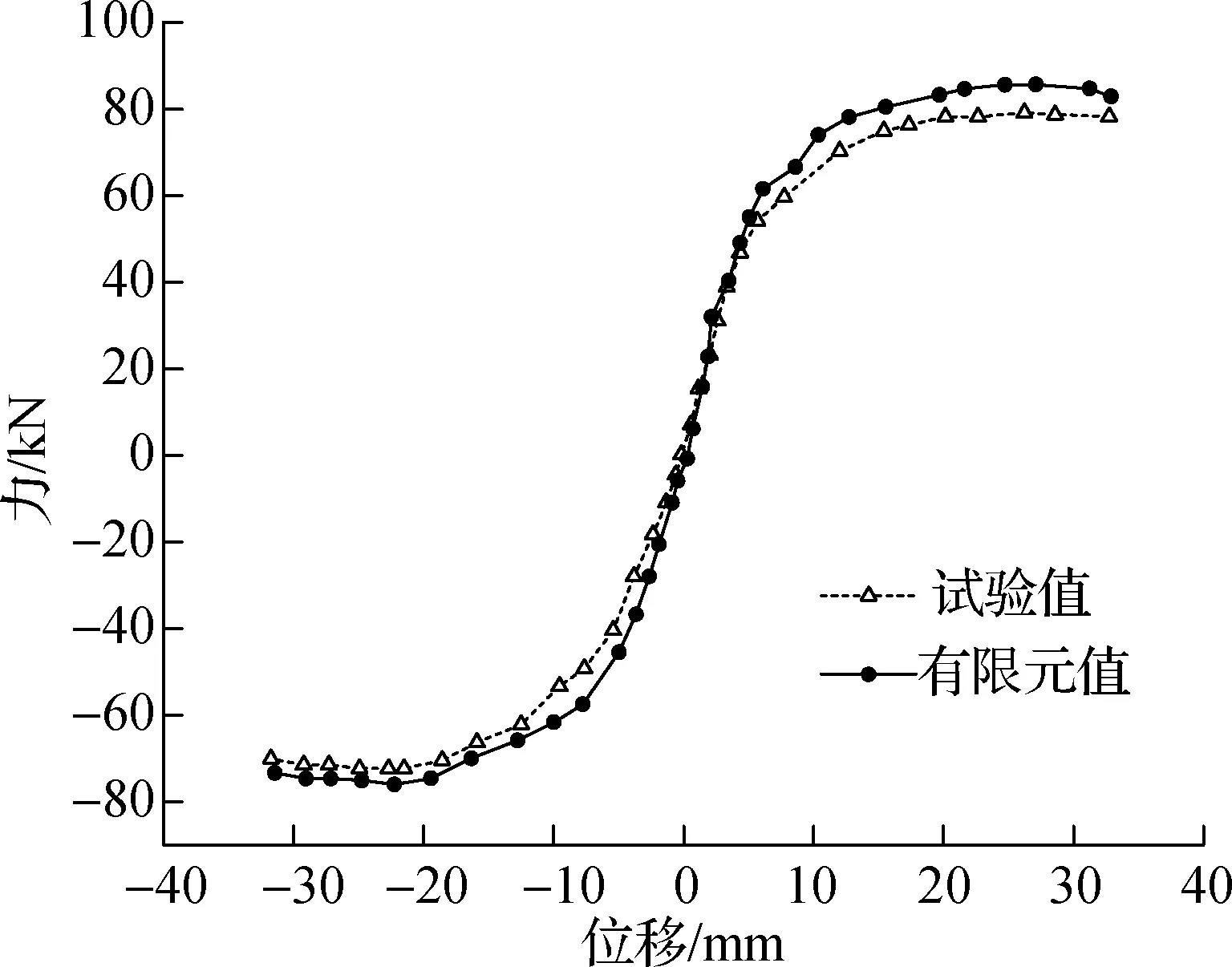
(b) 骨架曲线
2 高耗能黏弹性阻尼器腋撑对RC框架结构抗震性能的影响分析
2.1 滞回性能比较
部分加载工况(A=4 mm,f=0.05 Hz;A=24 mm,f=0.05 Hz;A=8 mm,f=0.5 Hz;A=32 mm,f=0.5 Hz;A=16 mm,f=1.0 Hz;A=40 mm,f=1.0 Hz)下试件RCF和VEDF框架的力-位移滞回曲线对比如图4所示.由图可知:
1) 加载幅值A=0~8 mm时,结构基本处于弹性状态,滞回环较扁,面积较小,能量耗散较小.试件VEDF在小位移幅值加载下就表现出明显的非线性,且滞回环明显比试件RCF饱满.随着位移幅值A的增大,试件RCF逐渐表现出非线性,且滞回环面积仍明显小于VEDF.这表明,高耗能黏弹性阻尼器腋撑在小位移下就有较好的耗能能力,且随着位移的增大,VEDF的滞回耗能能力显著提高.
2) 各加载工况下,试件VEDF滞回环的斜率均明显大于试件RCF滞回环的斜率,且随着位移幅值的增大,试件VEDF与试件RCF的斜率之差先逐渐增大后逐渐减小,表明加入高耗能黏弹性阻尼器腋撑可使钢筋混凝土框架结构的侧向刚度明显提高.
3)相同加载位移幅值下,试件VEDF滞回曲线对应的最大水平承载力明显高于试件RCF,表明加入高耗能黏弹性阻尼器可使框架结构的水平承载能力显著提高.
2.2 频率和位移幅值对滞回性能的影响
2.2.1 频率
在相同位移幅值、不同激振频率下试件RCF和试件VEDF的部分滞回曲线对比分别如图5和图6所示.由图可知,当激励位移幅值为A=0~32 mm 时,激励频率对结构滞回特性影响较大,当激励位移幅值为A=32~48 mm时,激励频率对结构滞回特性影响较小;当f=0~0.5 Hz时,激励频率的变化对结构的滞回特性影响不大,当f=0.5~3.0 Hz时,激励频率对结构的滞回特性影响较大;随着加载频率的增大,荷载值逐渐增大,滞回曲线逐渐饱满,耗能逐渐增大.这表明随着加载位移幅值的逐渐增大,试件的滞回性能对激励频率依赖性逐渐减小.
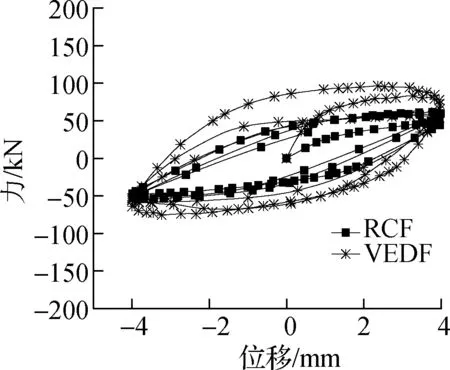
(a)A=4 mm,f=0.05 Hz

(b)A=24 mm,f=0.05 Hz
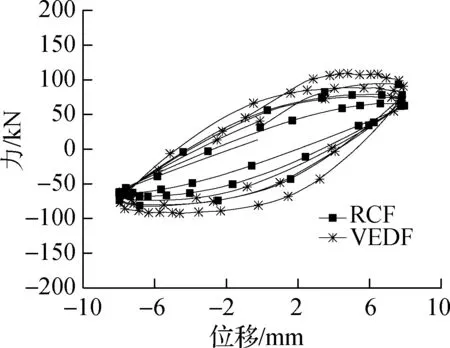
(c)A=8 mm,f=0.5 Hz
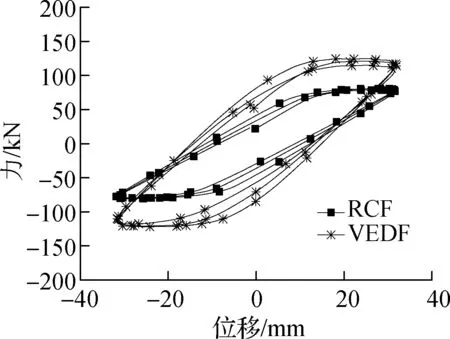
(d)A=32 mm,f=0.5 Hz
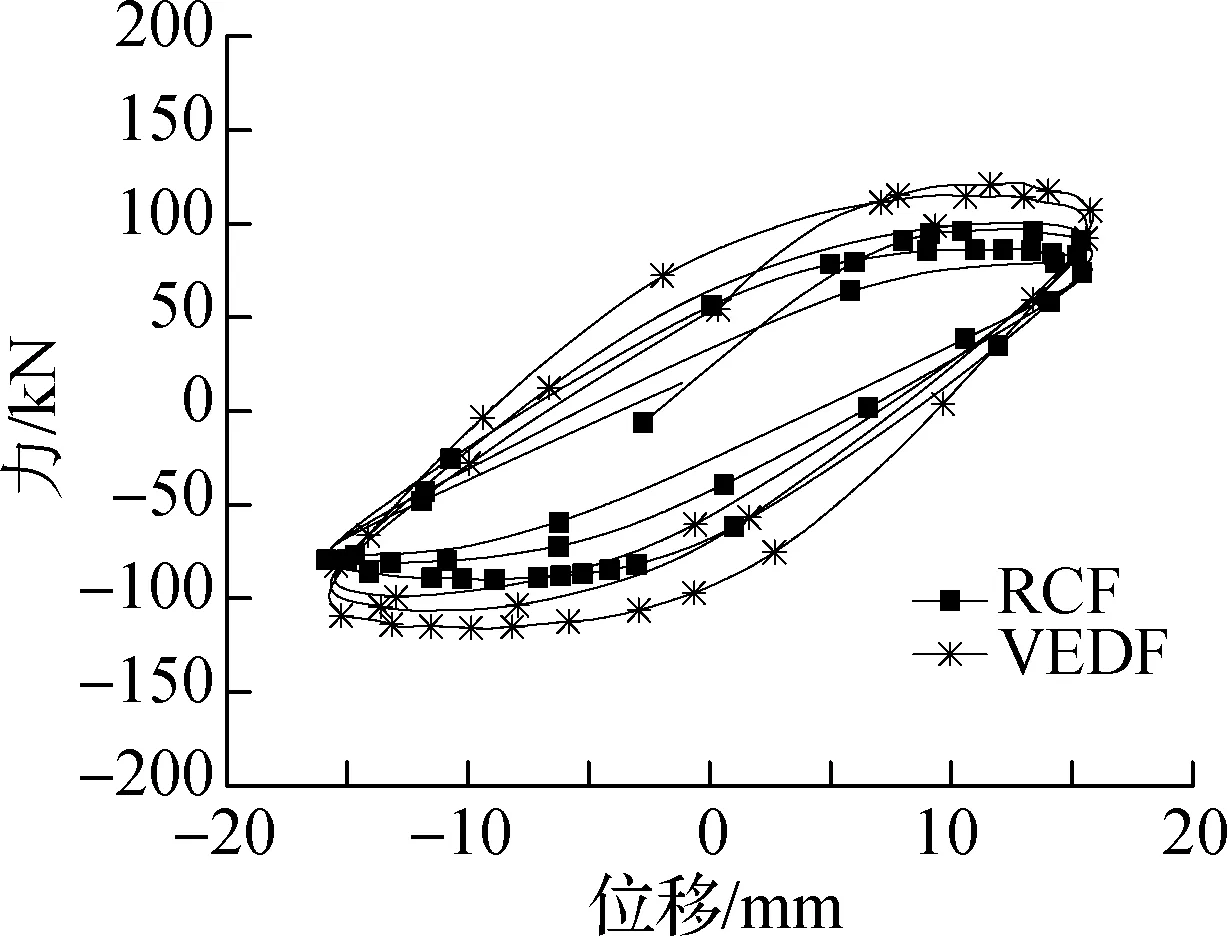
(e)A=16 mm,f=1.0 Hz
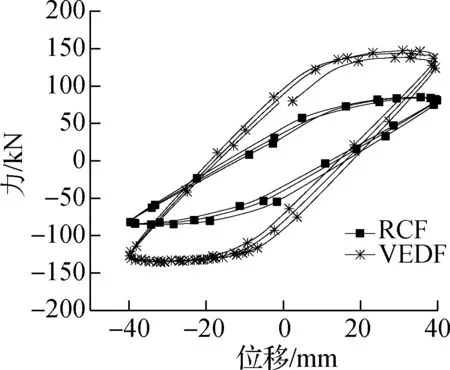
(f)A=40 mm,f=1.0 Hz
图4 试件 RCF和 VEDF在部分加载工况下滞回曲线对比
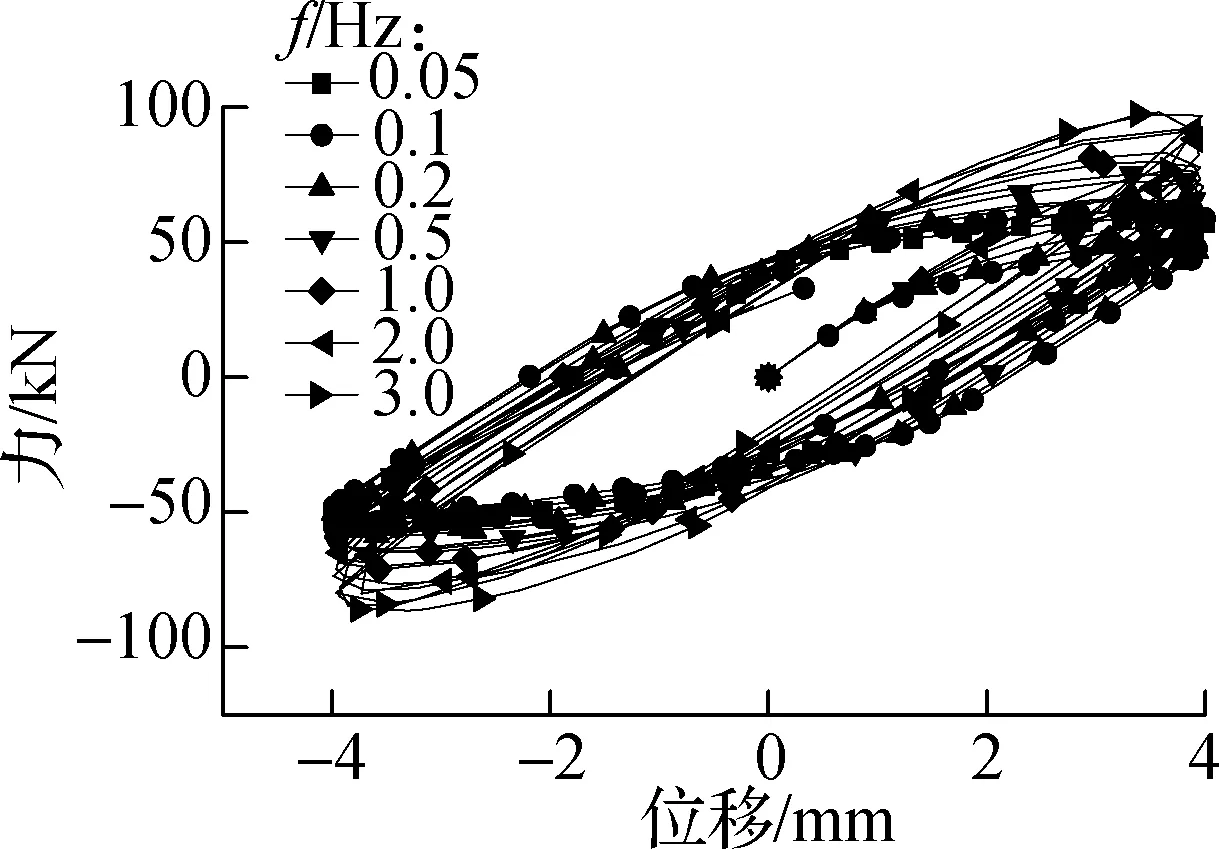
(a) A=4 mm
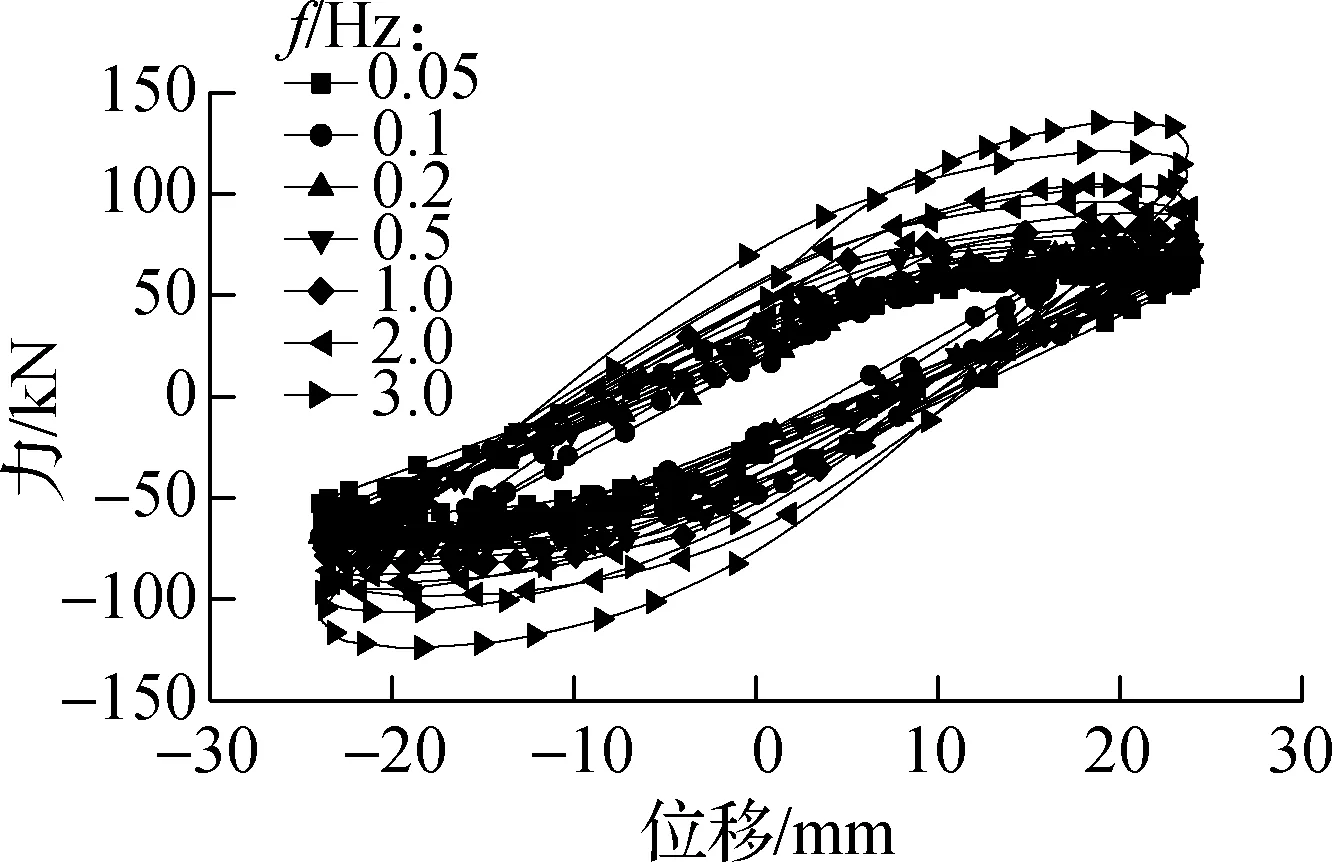
(b) A=24 mm
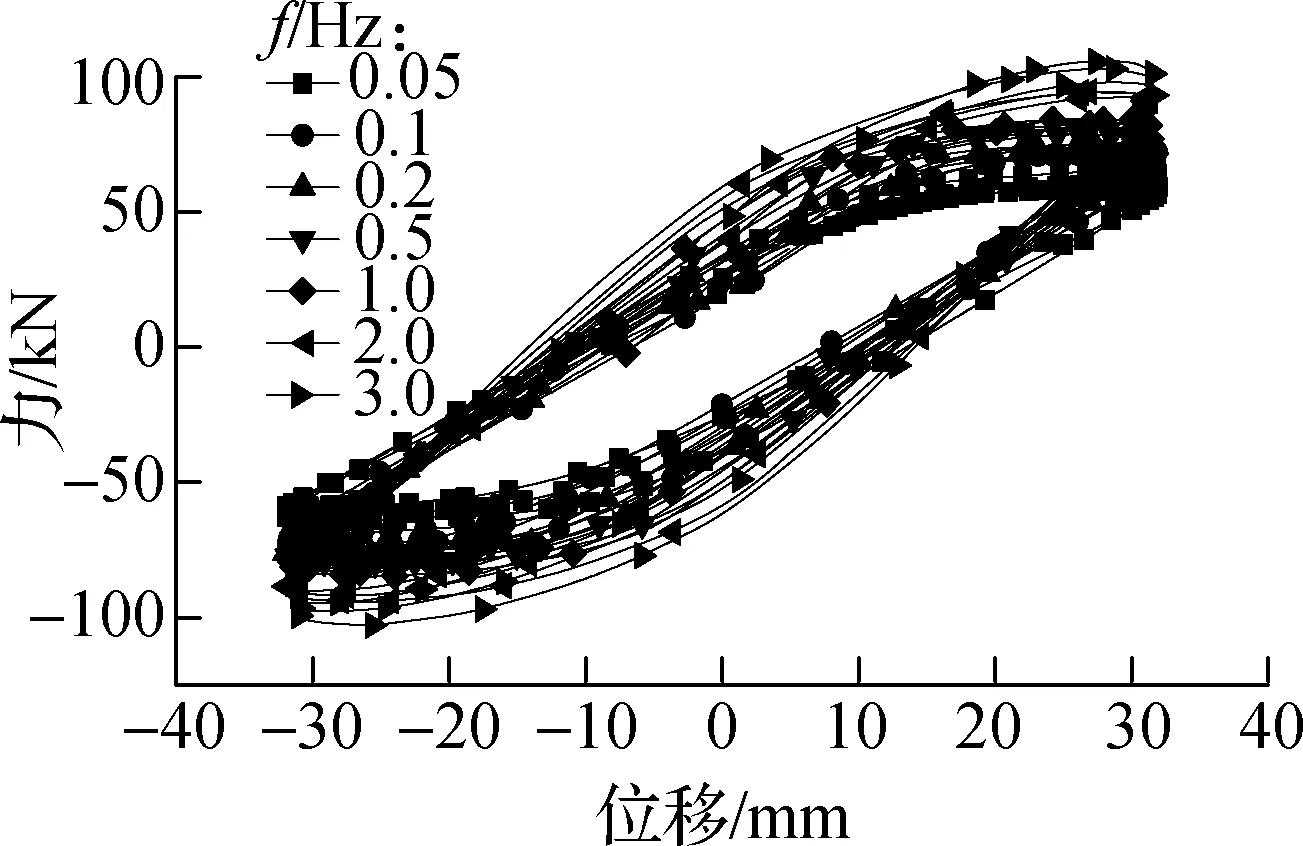
(c) A=32 mm
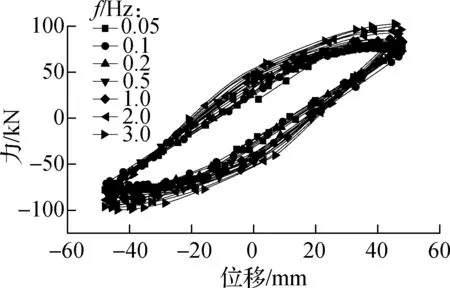
(d) A=48 mm

(a) A=4 mm
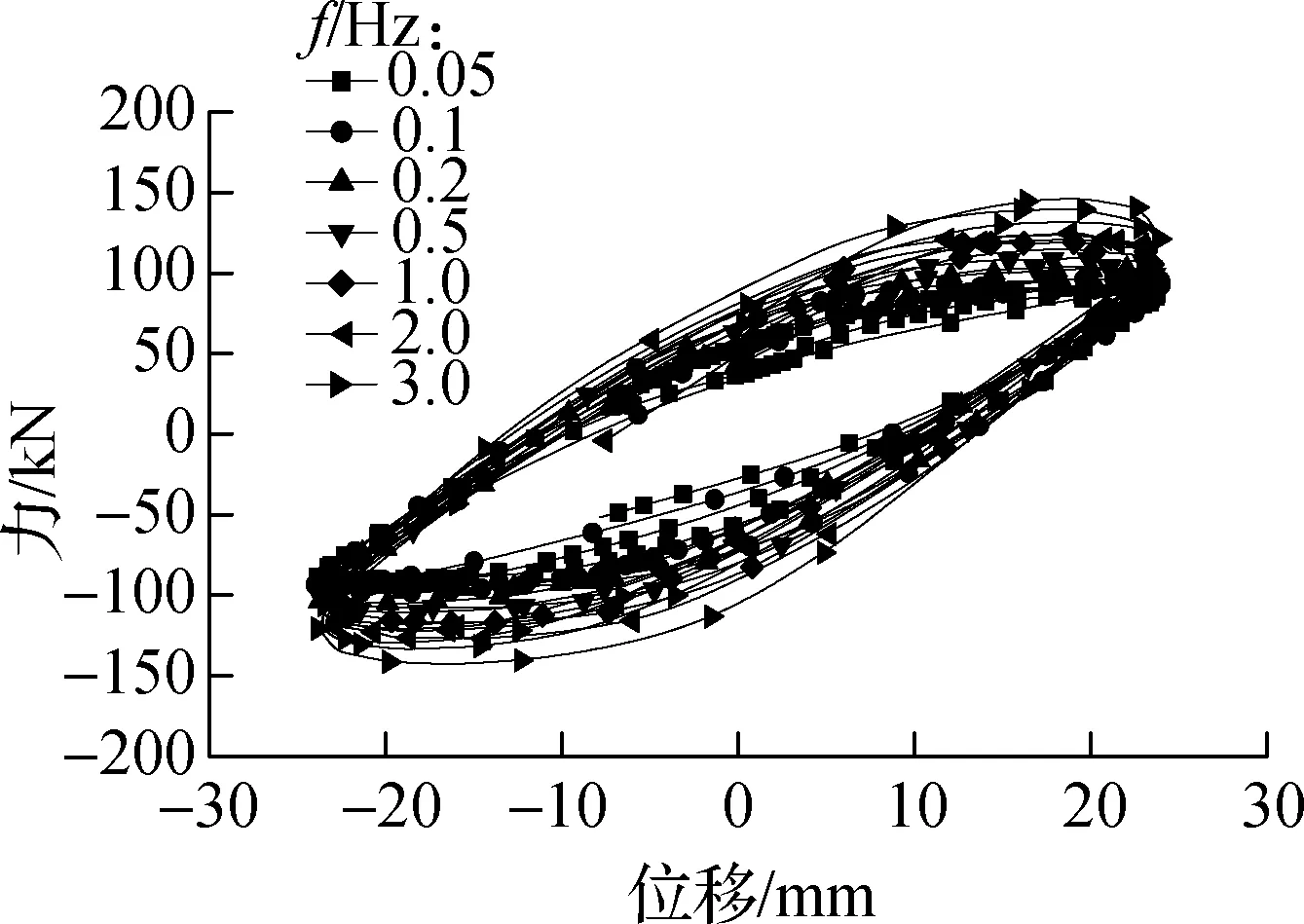
(b) A=24 mm
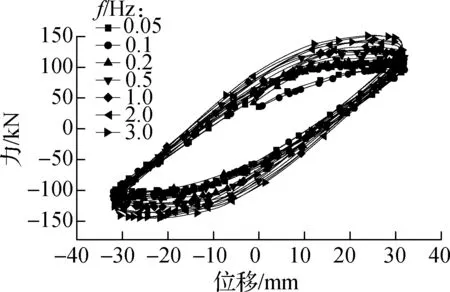
(c) A=32 mm
(d) A=48 mm
2.2.2 位移幅值
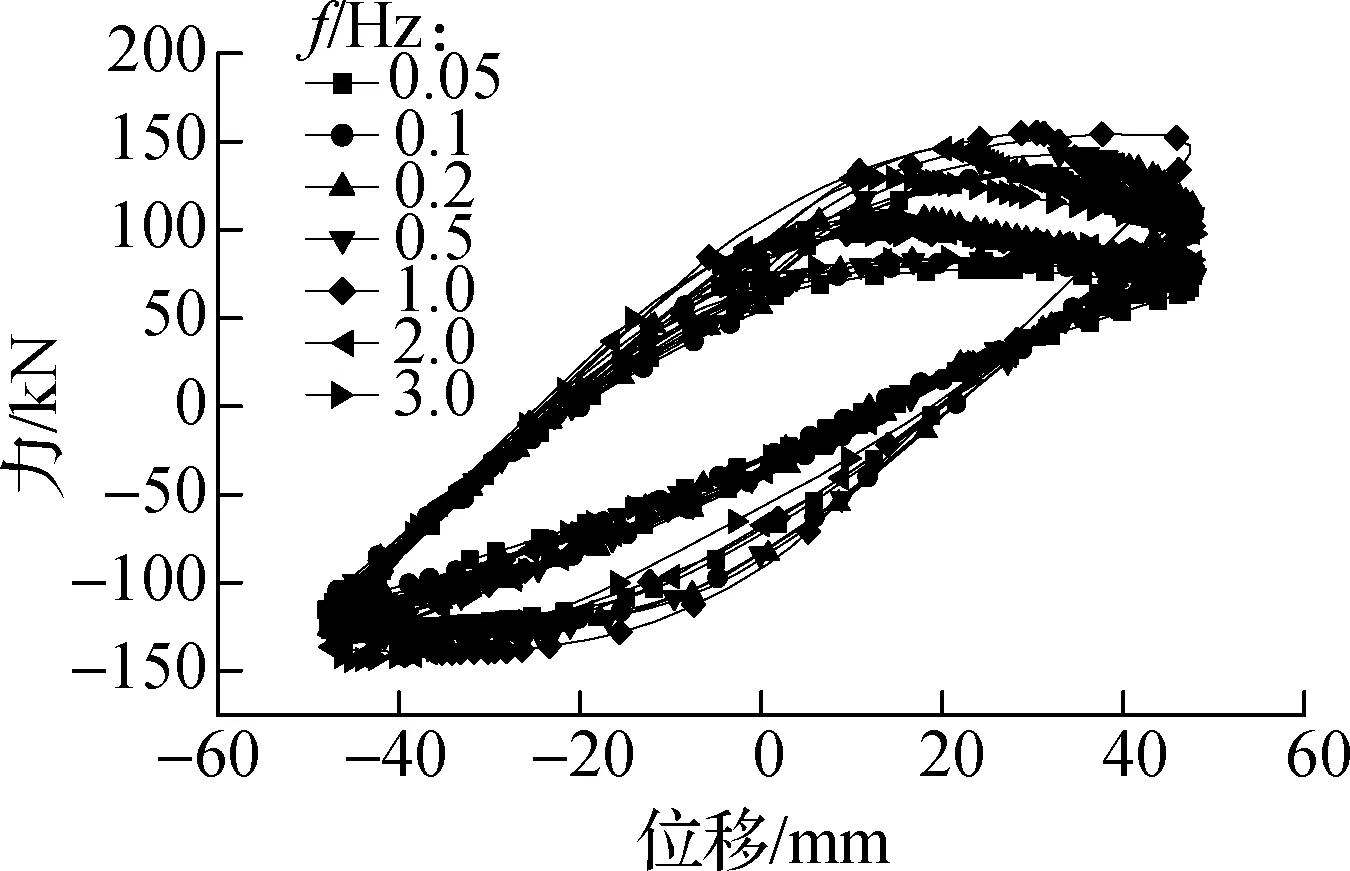
相同激振频率、不同位移幅值下试件RCF和试件VEDF的滞回曲线对比如图7所示.在各加载频率下滞回耗能随位移幅值变化的曲线如图8所示.由图可知,在各激振频率(0.05 Hz≤f≤3 Hz)和相同位移幅值下,试件VEDF均比RCF的滞回曲线明显饱满,试件VEDF的滞回环面积及承载力均明显大于试件RCF.试件RCF滞回耗能均随着位移幅值的增加而增大,试件VEDF滞回耗能均随着位移幅值的增加先增大后减小,位移幅值在A=40 mm时滞回环面达到最大.这说明加入高耗能黏弹性阻尼器腋撑的RC框架的耗能能力及承载能力显著提高.
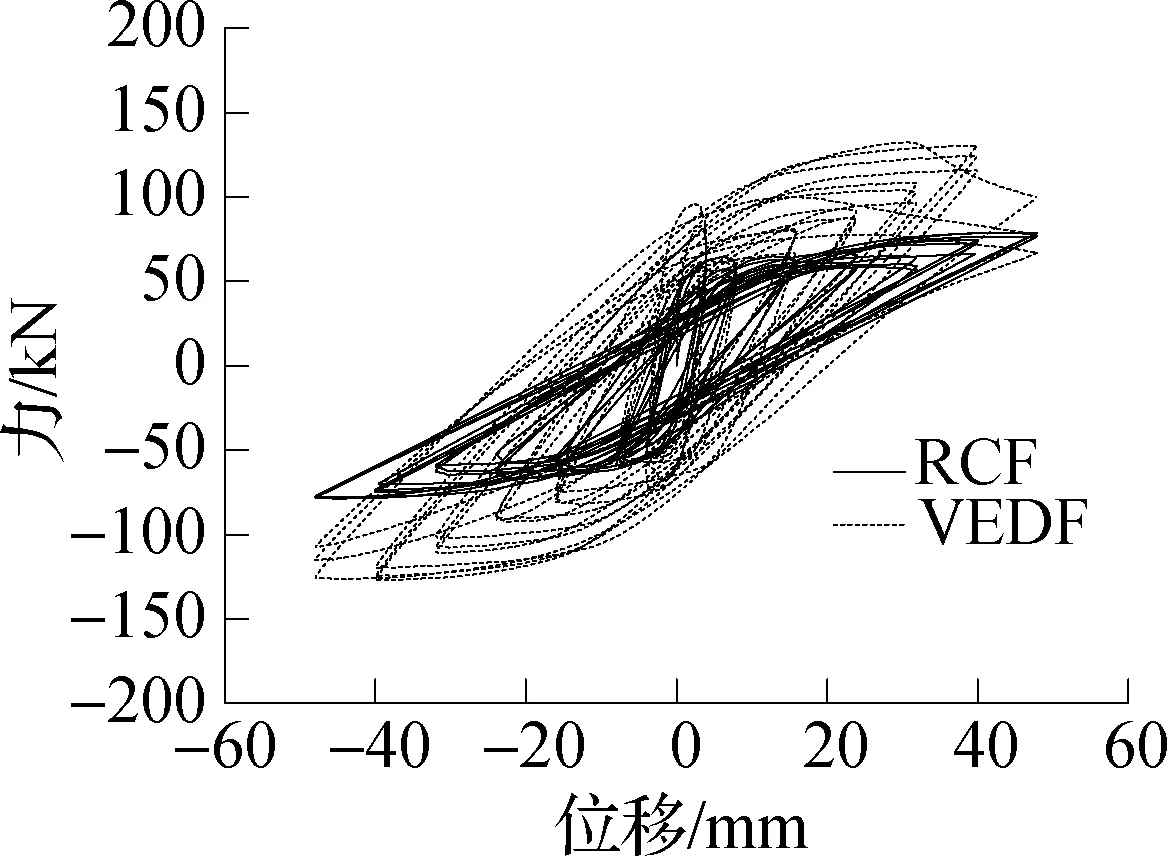
(a)f=0.05 Hz
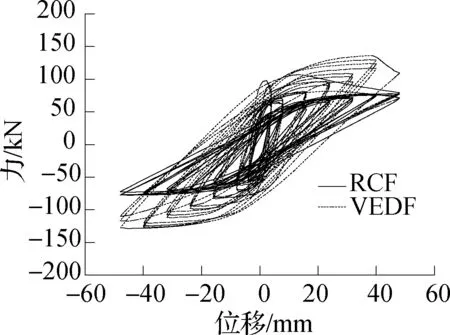
(b)f=0.1 Hz

(c)f=0.2 Hz
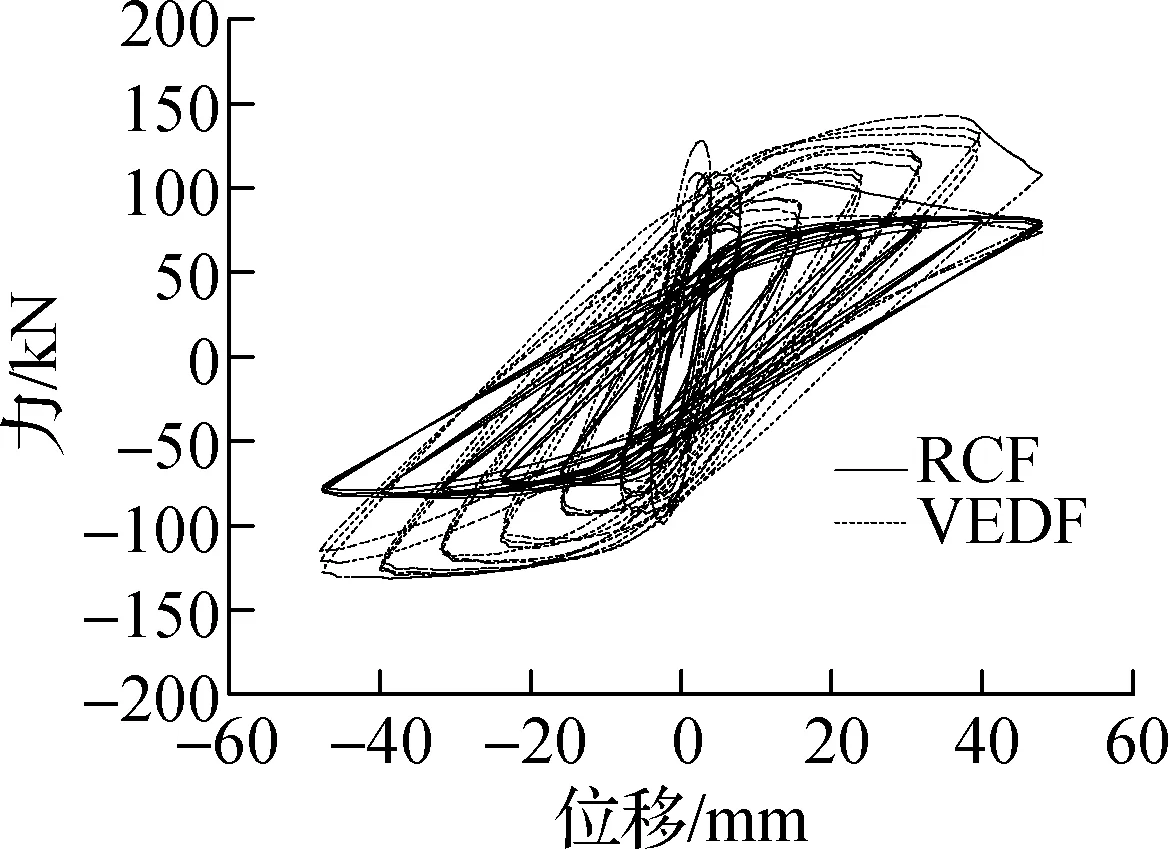
(d)f=0.5 Hz
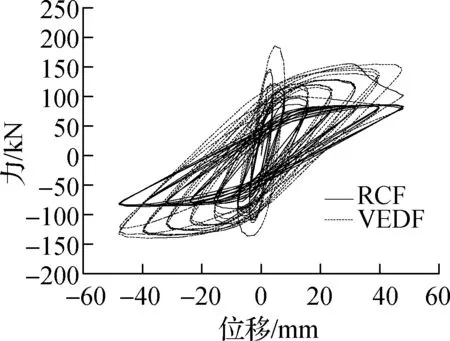
(e)f=1.0 Hz

(f)f=2.0 Hz
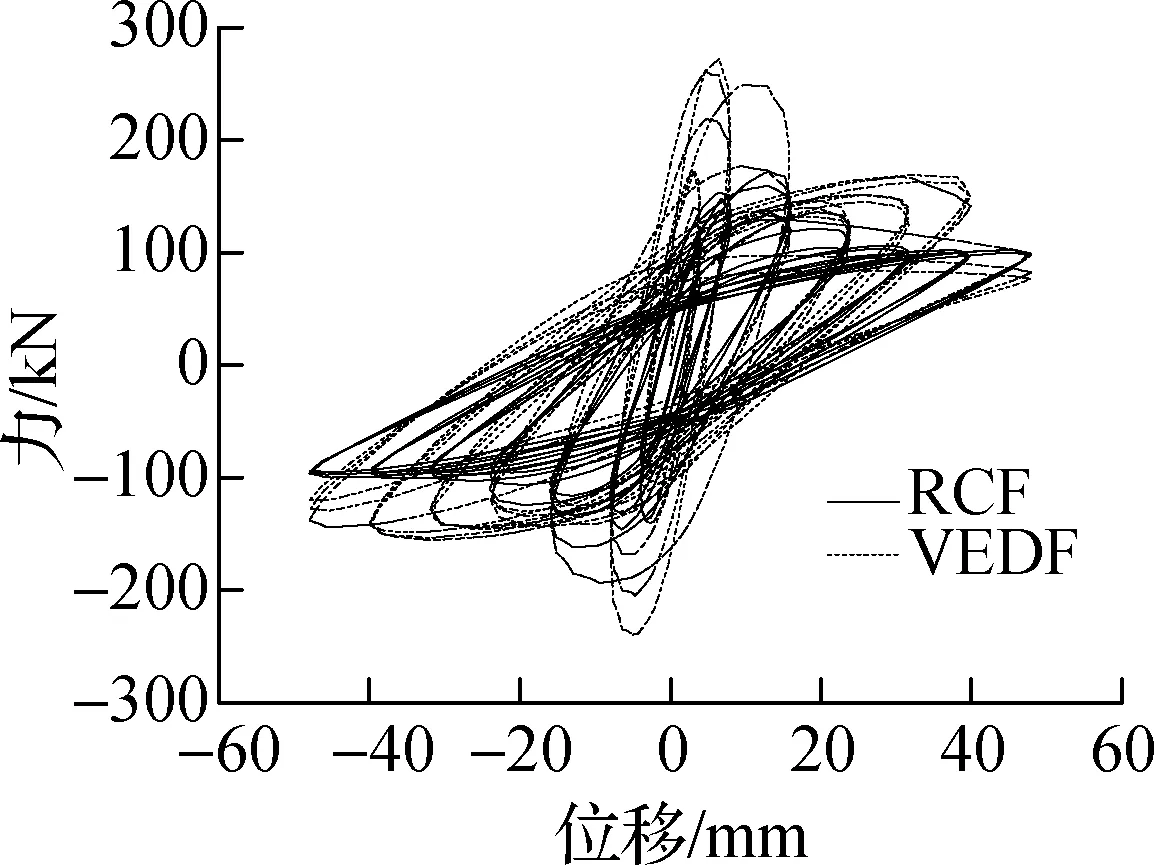
(g)f=3.0 Hz
图7 RCF和VEDF结构在相同频率、不同位移幅值下滞回曲线对比

图8 不同频率下试件滞回耗能-位移曲线
2.3 骨架曲线
试件RCF和VEDF在激振频率f=0.05,0.5 Hz时的骨架曲线对比如图9所示.由图可知,试件VEDF的初始刚度和承载力明显高于试件RCF,且VEDF的极限荷载较RCF的增幅最高可达68.3%.这表明加设高耗能黏弹性阻尼器腋撑可使框架结构的刚度和承载力显著增加,延缓了框架的损伤破坏.
2.4 刚度退化
结构或构件在不同位移控制点下不同循环周次之间的刚度退化可用割线刚度Ki来衡量[11].激振频率在f=0.05,0.5 Hz时试件RCF和VEDF的刚度退化曲线对比如图10所示.由图可知,VEDF的初始刚度均明显高于RCF,增幅最高可达45.57%.随着位移幅值的增大,2类试件正反向加载的割线刚度均呈下降趋势,初始下降幅度较大,后期逐渐趋于缓和,呈“八”字形下降.在同等位移幅值下,VEDF 的割线刚度均明显高于RCF.

(a) f=0.05 Hz

(b) f=0.5 Hz

(a) f=0.05 Hz
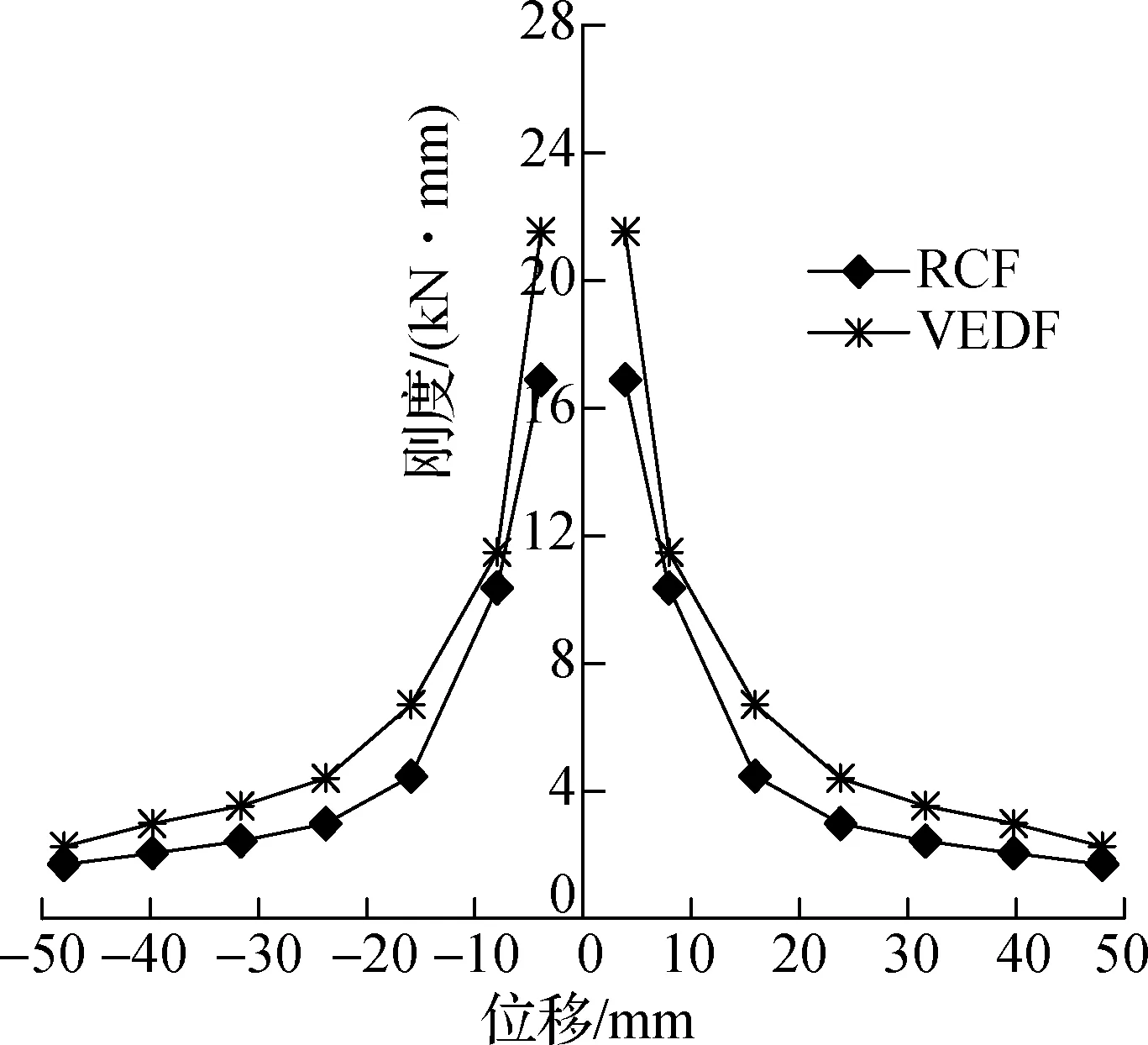
(b) f=0.5 Hz
2.5 耗能能力
在各加载频率下,试件VEDF与试件RCF的滞回环面积之比α以及试件VEDF中高耗能黏弹性阻尼器腋撑耗能占其总耗能的比例β随位移幅值A的关系变化曲线如图11所示.由图可知:
1) 在各加载频率下,在小位移幅值(A=4 mm)时,α,β均较大,最大值分别可达3.02和67.12%,表明带腋撑试件的耗能在小位移幅值下可达普通试件的3倍,其中腋撑的耗能占试件整体耗能可达67%;当加载幅值A=40 mm时,α,β最大值分别可达2.70和51.11%,表明带腋撑试件的耗能在大位移幅值下可达普通试件的2.7倍,其中腋撑的耗能占试件整体耗能可达50%以上;α,β均随着位移幅值的增大先减小再增大最后再减小,且在不同加载位移幅值下分别基本处于1.5和30%以上.这表明腋撑在小位移(小震)和大位移幅值(大震)下均可起到重要的耗能作用.
2) 在相同位移幅值下,α,β均随着加载频率的变化而有所变化.在小位移幅值(A=4 mm)时,均随着加载频率的增大而增大;在大位移幅值(A=40 mm)时,均随着加载频率的增大而减小.
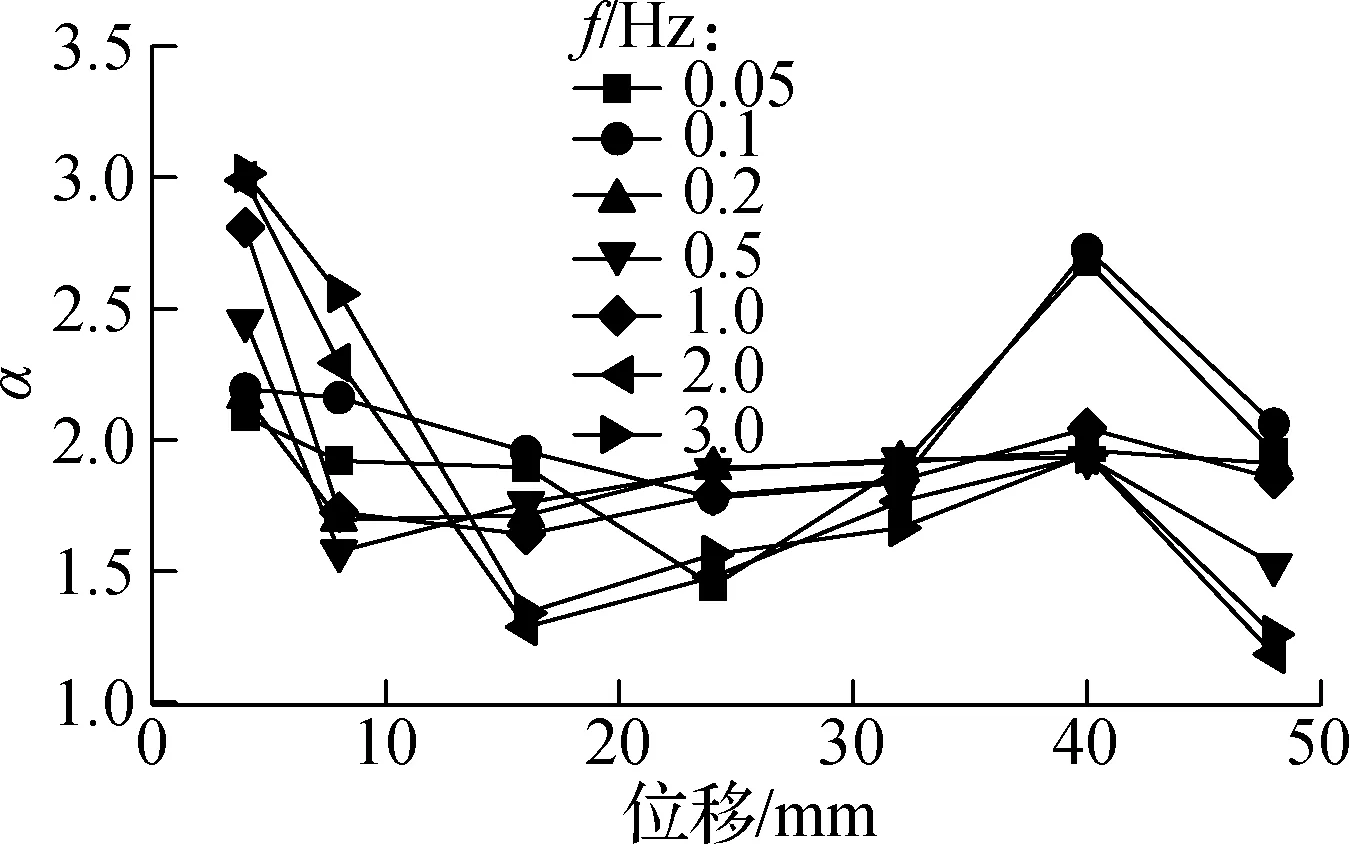
(a) α
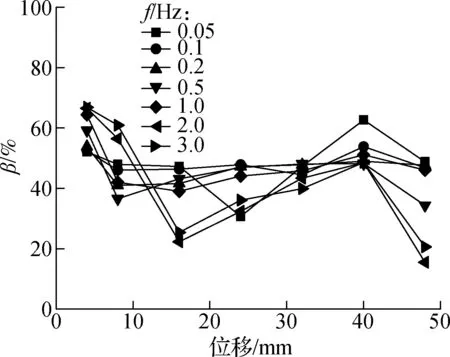
(b) β
2.6 附加有效阻尼比
根据下式计算出试件VEDF中高耗能黏弹性阻尼器腋撑的附加阻尼比ζa[12]:
ζa=Wc/(4πWs)
(4)
式中,ζa为VEDF的附加阻尼比;Wc为高耗能黏弹性阻尼器在结构加载位移下往复一周所消耗的能量;Ws为试件VEDF在加载位移下的总应变能.
ζa在各频率下随位移幅值的关系变化曲线如图12所示.由图可知,在各加载频率下,试件VEDF中腋撑的附加阻尼比ζa随位移幅值的变化规律基本一致,随着位移幅值的增大先减小再增大最后再减小.ζa在小位移幅值(A=4 mm)时,随着加载频率的增大而增大,最高可达16.06%;在大位移幅值(A=40 mm)时,随着加载频率的增大而减小,最高可达13.36%.结果表明,加设高耗能黏弹性阻尼器腋撑能较大幅度提高结构整体的耗能能力,VEDF中腋撑在小位移幅值(小震)高频下和大位移幅值(大震)低频下,能耗效率相对较高.
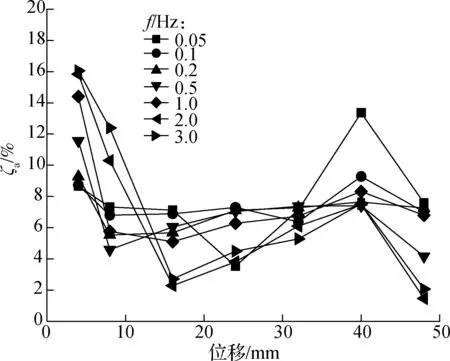
图12 不同加载频率下试件VEDF的ζa-位移曲线对比
2.7 关键部位点应变分析
本文取f=0.1,0.5 Hz工况,分别对框架柱底端、梁柱节点这些关键部位的钢筋应变进行分析.
2.7.1 框架柱底端应变分析
试件RCF 和试件VEDF在激振荷载作用下,框架柱底端纵筋的应变-时间曲线对比如图13所示,应变-位移曲线对比如图14所示.由图可知:
1) 当加载幅值A=0~32 mm时,试件VEDF的框架柱底端纵筋应变略大于试件RCF,且应变均处于弹性阶段;当加载幅值A=32~48 mm时,随着加载位移幅值的增大,试件VEDF框架柱底端纵筋应变突然快速上升,且试件VEDF纵筋应变大于试件RCF,很快达到塑性阶段.
2) 当频率f=0.1~0.5 Hz时,随着位移幅值的增大,加载频率对试件VEDF和RCF柱底纵筋应变在弹性阶段影响较小,进入塑性阶段影响大幅度增大,且试件RCF的最大应变不超过试件VEDF最大应变的46.64%.
3) 在相同加载频率下,随着加载位移幅值的增大,试件VEDF和试件RCF钢筋应变均逐渐增大.在相同加载幅值下,钢筋应变处于弹性阶段(A=0~32 mm)时,试件VEDF柱底端纵筋应变略大于试件RCF;钢筋进入塑性阶段(A=32~48 mm)时,试件VEDF柱底端纵筋应变放大效应大幅度增加.
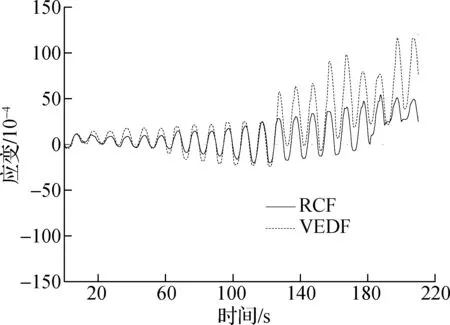
(a) f=0.1 Hz

(b) f=0.5 Hz

(a) f=0.1 Hz

(b) f=0.5 Hz
以上表明加设高耗能黏弹性阻尼器腋撑后,框架柱底端纵筋应变有一定的放大作用,且纵筋处于弹性阶段放大效应较小,而进入塑性阶段放大效应较大.
2.7.2 框架梁柱节点应变分析
试件RCF和试件VEDF在激振荷载作用下框架梁柱节点箍筋的应变-时间曲线对比如图15所示,应变-位移曲线对比如图16所示.由图可知:
1) 在加载的全过程中,试件VEDF框架梁柱节点箍筋的应变均远小于试件RCF,且试件VEDF节点箍筋处于弹性阶段.
2) 当频率f=0.1~0.5 Hz时,加载频率对试件VEDF梁端纵筋应变影响不大.试件RCF随频率增大,应变有所增大.
3)在相同加载频率下,随着加载位移幅值的增大,VEDF钢筋应变变化不明显,而试件RCF钢筋应变逐渐增大;在相同加载幅值下,试件VEDF柱端箍筋应变的应变均远小于试件RCF,应变减幅可达90%以上.
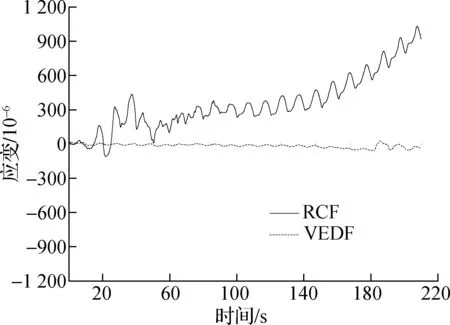
(a) f=0.1 Hz
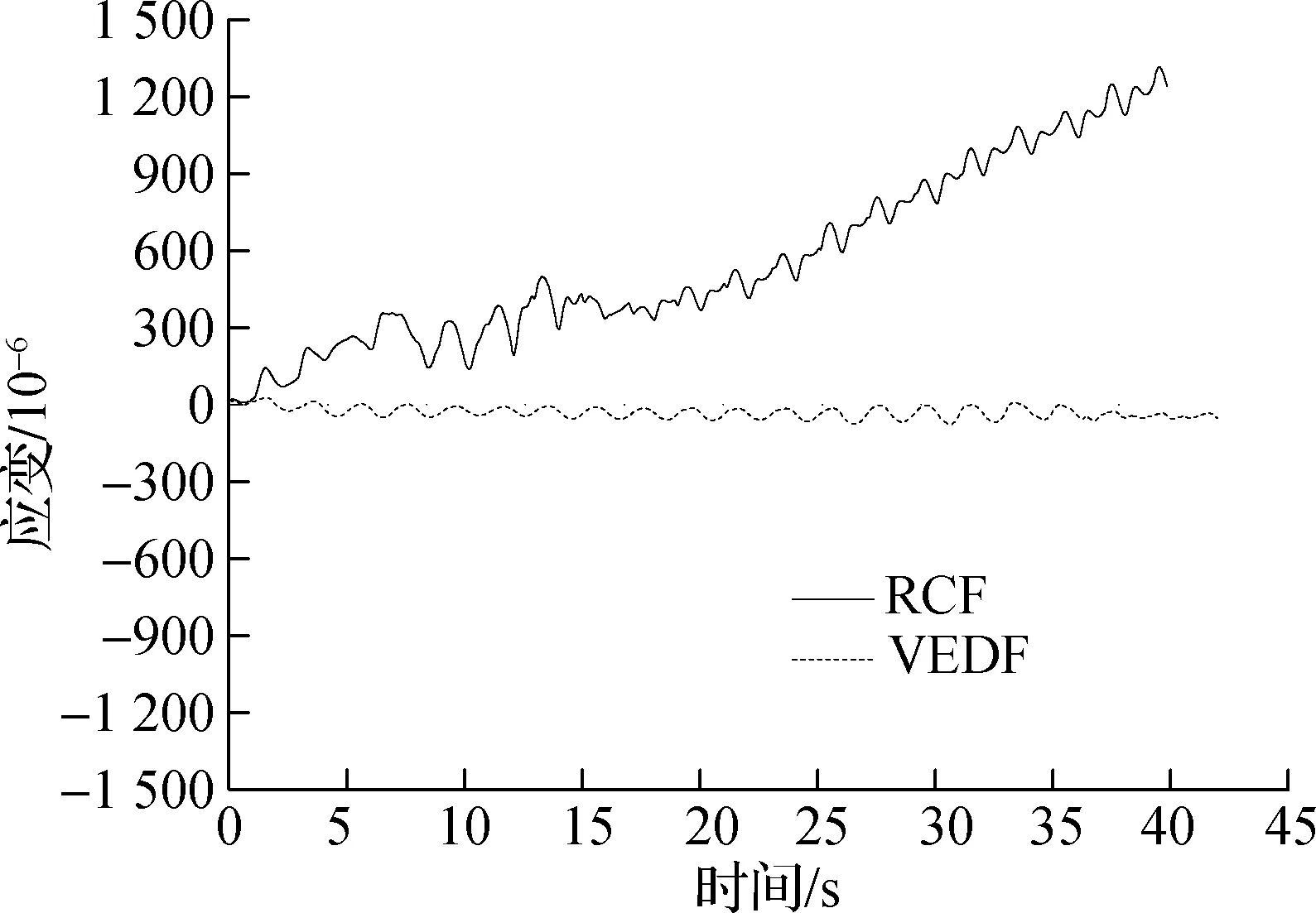
(b) f=0.5 Hz

(a) f=0.1 Hz
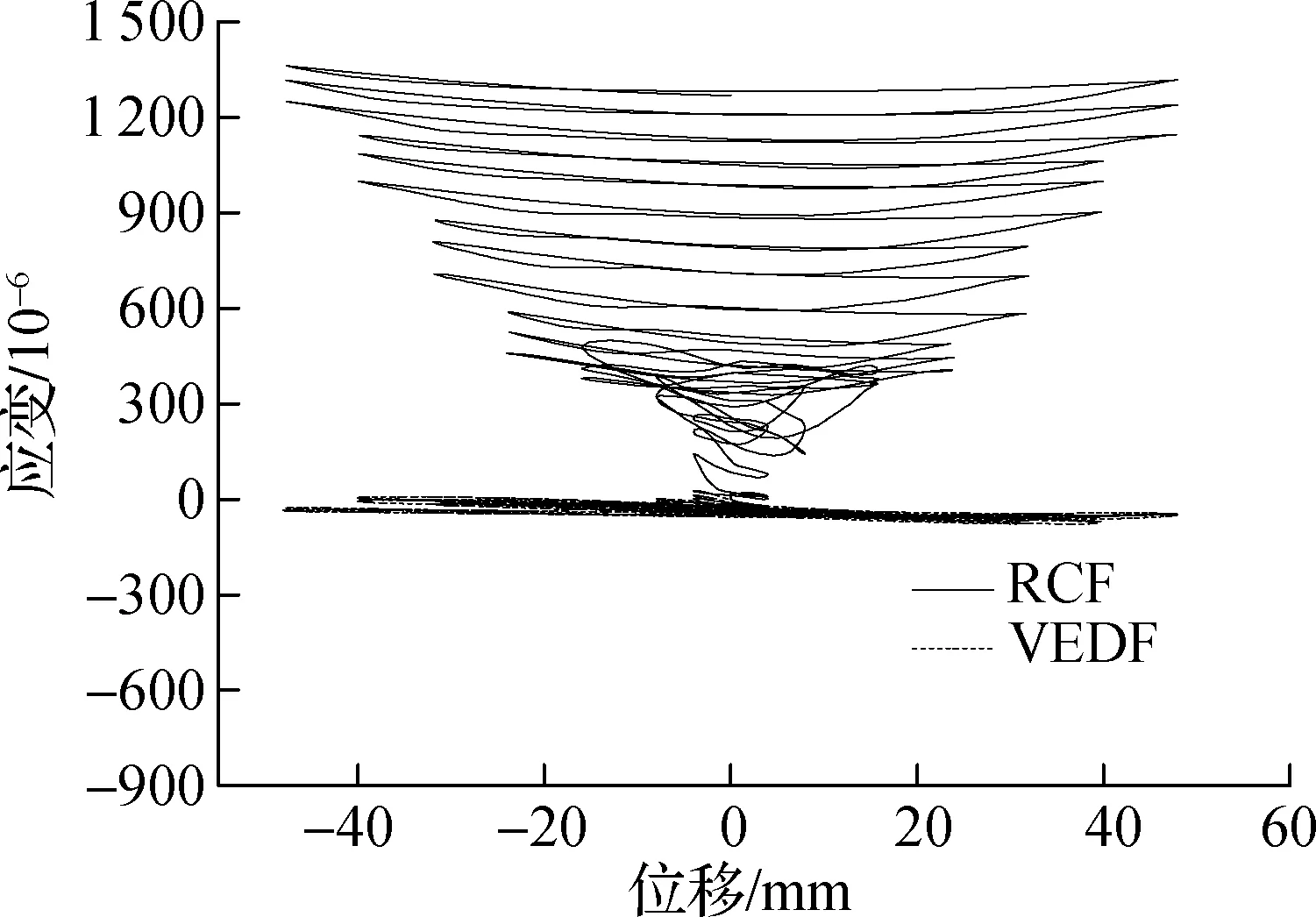
(b) f=0.5 Hz
以上表明加设高耗能黏弹性阻尼器腋撑后,梁柱节点箍筋应变减小显著,且大位移幅值下应变依然较小,处于弹性阶段,对梁柱节点区起到了较好的保护作用.
3 结论
1) 加设黏弹性阻尼器腋撑的RC框架的滞回曲线较普通框架饱满,且能较大幅度提高结构的耗能能力、承载力和侧向刚度,可给结构提供较大的附加阻尼比,对结构承载力退化和刚度退化的抑制效果显著.
2) 在本文研究的加载频率内,2类框架随着位移幅值的逐渐增大,试件的滞回性能对频率的依赖性逐渐减小.钢筋处于弹性阶段时,加载频率对其应变影响不大,而处于塑性阶段时,加载频率对其应变影响很大,随着频率的增加应变逐渐增大.
3) 在各级位移幅值下,腋撑均起重要耗能作用,且小位移幅值下也表现出很好的耗能效果.在各相同加载位移幅值下,随着加载频率的增大,腋撑耗能有一定程度的提高.
4) 加设黏弹性阻尼器腋撑改变了框架结构的受力模式,减小了梁柱节点部位的受力,延缓了框架梁柱节点区域损伤的产生和发展,有效地保护了梁柱节点,满足了“强节点弱构件”的抗震设计要求,但会使柱底的内力有所加大,且2类框架均为柱底损伤发展严重而导致结构最终破坏,这部分区域是抗震设计及加固的重点区域.
