基于数据关联与轨迹评估的多目标跟踪

程艳云 朱松豪 Huet Alexis Pierre René

南京邮电大学

0 引言

多目标跟踪问题可描述为在一系列图像中同时跟踪多个移动目标，且能随着时间推移，确定不同目标的身份。目前基于检测的多目标跟踪主要面临两个难题：

（1）为每一个目标分配一个唯一的ID标号，或者确定该目标为误报；

（2）每一个轨迹能够合理地解释目标的运动状态。

以上两个方面都具有一定的挑战性，然而目前的研究目标主要集中在解决其中的一个方面，或者另一方面。

数据关联是一个组合问题，典型的方法是简化模型或者设定满足于特定目标函数的近似解。当前是将检测器响应与目标的实际位置相关联，从而表示目标的实际轨迹，这不利于建立目标的动态模型，特别是在一些漏检的图像帧中，例如长期的目标遮挡。另一方面，目标轨迹的评估还需要考虑动态变化、持久性以及轨迹互斥等因素。由于数据关联需在高维空间中最小化多模态能量函数，这是一个相当大的挑战。此外，把待确定的观测与特定的目标相关联，也是一个很难完成的任务。

本文从时间和空间的角度建立CRF模型，将目标的数据关联与轨迹评估整合到同一个CRF模型中，构建离散-连续能量函数，通过求取最小能量确定目标的最佳运动轨迹。本文在借鉴多标号成本的基础上，提出了融合多模型拟合和全局轨迹特性的多目标跟踪方案。数据关联通过CRF模型来实现；此外，还通过空间互斥模型来限制同一物理空间两个不同的观测。针对轨迹评估，本文从时间上对相邻两帧的目标标号进行约束，轨迹模型采用连续光滑的曲线来表示，同时在连续域中拟合一系列观测目标。对于给定的一系列轨迹假设，使用带有贪婪标号移除的α-expansion算法更新标号，以及采用梯度下降法对目标的轨迹进行优化。

1 基于CRF模型的目标标号

与其他常见的前景检测方法类似，本文基于HOG与LBP联合特征提取方法，然后使用线性SVM进行前景和背景分割，得到一系列假定的前景观测D。然后把观测作为输入数据，建立CRF模型，具体步骤如下：

（1）将每一个观测看成一个顶点V，对其分配一个唯一的ID标号；若为背景，则统一标号为ɸ；

（2）将同一帧图像中的不同观测用空间互斥边EX相互连接；

（3）相邻两帧图像，如果观测之间的两两距离小于特定的阈值τ，则使用时间平滑边ES相互连接；

本文的主要任务包括数据关联与轨迹评估两个步骤。数据关联通过离散多标号CRF模型来表示，而轨迹评估通过连续光滑的曲线模型来表示。此外，从两个不同方面说明了目标之间的互斥现象。首先从空间上，通过引入竞争检测二元项来避免数据误读现象。然而，仅仅空间上的约束是远远不够的。因此，在时间上也采取了一些互斥方法，当同一时刻的两个不同目标轨迹发生重叠时，本文还引入了一种新颖的二元共生标号成本。

1.1 符号注释

D为一系列假设目标，dgt表示第t帧图像中的目标g，wgt为置信度值。Pgt∈R2为第t帧图像中某个观测目标的位置，(xi,yi)为对应的参考平面坐标。T={T1,T2,…,TN}表示所有假设目标轨迹，其数量远大于场景中目标的实际数量。对于给定的标号集l，ld∈L={1,2,....，N,ɸ}，其中L表示所有假设轨迹的标号集。若某个观测目标属于前景，则ld∈L={1,2,....,N}；若为误报，则 ld=ɸ。表示场景中所有观测目标的有效轨迹；Ɛ=ƐS∪ƐX表示所有CRF模型的边，其中ƐS表示相邻两帧图像中，所有观测目标之间距离小于特定阈值τ的时间平滑边，而ƐX表示同一帧图像中不同观测目标之间的空间互斥边。

1.2 多目标跟踪的能量函数

在计算机视觉领域，多标号问题可以被描述成最大后验估计(MAP)，可以通过由顶点和边构成的CRF模型G={V,E}来描述，并分别求CRF中顶点和边的最小能量。鉴于此，本文将每一个检测到的观测d∈D看成是CRF模型中的顶点V，两个相邻的顶点用一条边Ɛ相互连接。然而，目的不仅仅是预测离散标号集体l，还包括目标的连续轨迹T。本文多目标跟踪的离散-连续能量函数如公式（1）所示：

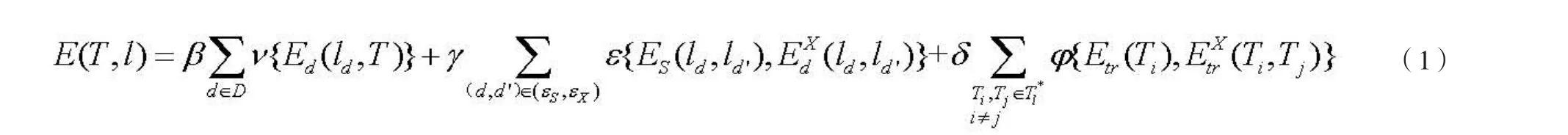
其中β，γ，δ表示各部分能量所占的权重，在实际实验中，可以通过调节能量函数前的权重改变跟踪的效果。v{Ed(ld,T)}表示轨迹拟合成本，Ɛ{ES(ld,ld’),EdX(ld,ld’)}表示由边 Ɛ 产生的成本，ES(ld,ld’)表示相邻两帧属于同一条ƐS的标号不同时产生的成本，EdX(ld,ld’)表示同一帧图像中两个观测标号相同时产生的成本，φ{Etr(Ti),EtrX(Ti,Tj)}表示单个轨迹和互斥轨迹共同产生的成本，Etr(Ti)表示单个目标的轨迹成本，EtrX(Ti,Tj)表示互斥轨迹产生的成本。为了方便表示，公式中

目标函数旨在找到一组能使E(T,l)取得最小能量的标号集与跟踪轨迹的状态：(T×,l×)=argmin(T,l)E(T,l)，本文先固定标号集l，然后对目标的轨迹进行连续优化；然后再固定轨迹集T的相关参数，对标号l集进行离散优化。首先详细介绍连续轨迹的表示模型与每一项能量分量。

1.3 轨迹评估

与之前许多单纯的离散多目标跟踪方法相比，本文采用连续的光滑曲线表示目标的运动轨迹，如图1所示。其中，左端点为起始帧si，右端点为结束帧ei。

图1 二维连续轨迹模型图

每个轨迹的二维线条表达式如公式（2）所示：

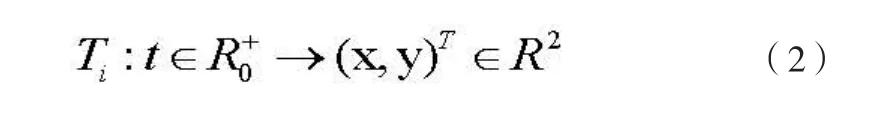
其中(x,y)T表示目标i在t时刻的位置，对应于图1中的离散点。

假定每个目标的轨迹具有若干个片段，相关参数通过系数矩阵Ci∈R2cix4来表示。轨迹片段的数量取决于每个目标轨迹的长度F(i)，本文中轨迹片段的数量设置为max(1,[F(i)/15])，其中[.]表示四舍五入，F(i)=ei-si+1。为了抑制轨迹端点处的观测误分配给其他轨迹，因此采用外推法进行限制，即t∈[si-Δ,ei+Δ]，本文设置 Δ=3。

假定已经固定了数据关联项l，于是argminTEl(T)=argminTE(T,l)。因此，轨迹评估的最小能量函数如公式（3）所示：

其中Ed(ld,T)表示带有标号l的观测与该目标实际轨迹的拟合程度。Etr(Ti)表示单个目标的轨迹，只有当该轨迹属于有效轨迹 Tl× 时，即的成本才产生，例如该轨迹中至少有一个观测目标被标号为前景，标号方式与规范一致。EtrX(Ti,Tj)表示目标i和j轨迹重叠时产生的成本。

（1）拟合轨迹

Ed(ld,T)表示某个观测目标d∈D属于该目标轨迹的一元数据成本，衡量标准为该观测与其轨迹之间的最短距离。此外，该项还能表示该观测目标是否属于误报。为了方便起见，将观测目标dgt统一用d来表示。定义第t帧图像中的轨迹拟合成本如公式（4）所示：

其中wgt表示观测目标的置信度值，pgt表示该观测的位置，Dis(.)表示距离函数，即观测目标距离其轨迹的最小距离。当某个检测结果的标号为l=Φ，此时产生成本λΦ×wgt只与数据关联有关，表示误将背景当成目标。

为了使得公式（5）能基于梯度算法进行优化，本文采用可微分的欧氏距离函数，同时为了防止微分后的分母为零，距离函数中加上一个很小的微调参数Ɛ=0.1，函数定义如公式（5）：

（2）先验轨迹

目标i的轨迹先验能量函数由以下几个方面组成，如公式（6）所示：

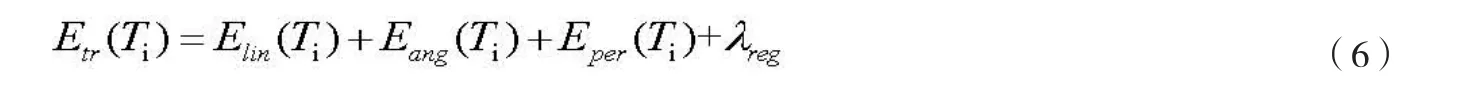
其中Elin(Ti)表示目标i的线速度能量，Eang(Ti)表示目标i的角速度能量，Eper(Ti)表示目标i轨迹的持久性能量，λreg为轨迹修正模型的能量，为了防止迭代过程中的过拟合。上式中的每一项都可微。

所有目标的运动都应该合乎一定的物理限制，即在同一时刻，同一物理空间不可能有两个观测目标。本文所用的动态模型是建立在目标的角速度和线速度缓慢变化的基础上进行的。为了和之前的定义相对应，设x=x(t)，y=y(t)作为参考平面曲线的坐标，x’(t)，y’(t)为一阶导数，x’’(t)，y’’(t)为二阶导数。

假定行人最可能以大约1.2m/s的匀速移动。如果偏离这个速度，就进行二次惩罚。因此，线速度模型的表达式如公式（7）所示：

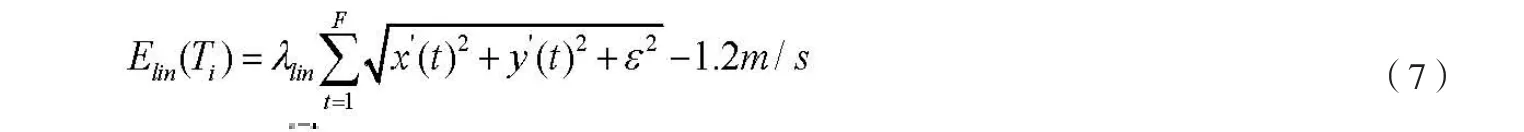
除了目标的线速度模型，本文还给出了目标的角速度模型，t时刻目标的角速度通过公式（8）给出：

其中Ɛ=0.1，通过以上变形，得到目标i的角动态轨迹模型，如公式（9）所示：

当目标进入特定的跟踪区域，会产生不同程度的出现或者消失。目标的轨迹总是开始或者终止于预定义感兴趣区域的边界。本文通过以下“sigmoid”函数对轨迹的持久性进行修正，如公式（10）所示：

其中B(Ti1)表示第i条轨迹的起点与最近的跟踪区域边界间的距离，B(TiF)表示第i条轨迹的终点与最近的跟踪区域边界间的距离。参数u=1/s，试验中s=35cm。该措施有利于目标遮挡后的轨迹恢复，有效地避免了因遮挡而发生跟踪轨迹突然中断的现象。

（3）互斥轨迹

在所有的图像帧中，不同目标之间的轨迹在空间上不应该重叠。本文引入一种二元标号成本思想。如果同一物理空间中的不同目标轨迹发生重叠，则对该轨迹对进行一定的惩罚，如图2所示

图2 不同目标轨迹相互重叠的示意图

针对每一对有效轨迹Ti,Tj∈Tf×(i≠j)，则产生相应的二元标号成本EtrX(pairwisecost)。当两个目标比较接近时，对应的惩罚成本接近无穷大，如公式（11）所示。

其中X(Ti,Tj)表示轨迹i与j在时间上的重叠，s=35cm表示检测框的宽度。

1.4 数据关联

数据关联是给每一个观测d∈D分配一个唯一的ID标号，并确定该观测属于某个目标i的轨迹，或者属于误报(ɸ)。鉴于此，若把等式(1)中的轨迹假设部分先固定，则数据关联部分的最小能量公式等价于公式（12）：

其中 ES（ld,ld’）

与EdX(ld,ld’)是由两种类型的二元边Ɛ=ƐS∪ƐX引起的能量。ES（ld,ld’）表示时间平滑边ƐS的成本函数，即相邻两帧图像中观测标号不同时产生的成本。EdX(ld,ld’)表示空间平滑边ƐX的成本，即同一帧图像中出现相同标号时产生的成本。

（1）时间平滑边ƐS与空间互斥边ƐX

时间平滑边ƐS提供数据关联的时间平滑度。

相邻两帧图像中，如果观测之间的两两距离小于特定的阈值τ，则使用时间平滑边ƐS连接，表达式如公式（13）所示：

其中F表示视频的帧数，该措施使得相邻两帧图像中同一个目标具有相同的标号。在能够保证足够的目标动态情况下，阈值τ尽可能的大。

在同一帧图像中，空间互斥边ƐX能够确保同一帧图像中每一个观测目标的标号唯一。另一方面，对于那些非常相似的观测，采用多个边也是合理的，因为即使是进行了非最大化压缩，检测器有时候也会错误的产生来自同一个目标的多个输出，如公式（14）所示。

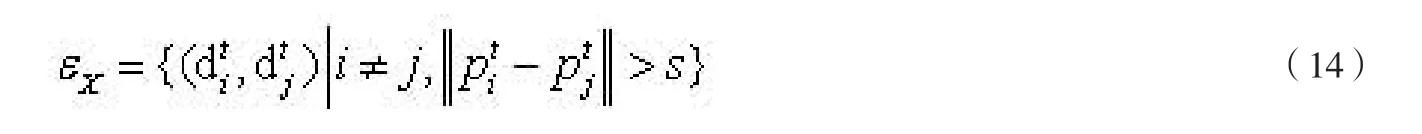
其中pit∈R2为观测dit∈D的坐标（xi,yi），s表示矩形检测框的宽度。

如图3所示，绿色结点代表观测器响应的随机变量，蓝色结点表示二元能量成本，为了方便表示，图中给出了部分能量。红色的边表示时间平滑因子ƐX，灰色的边表示空间间互斥因子ƐS。

图3 CRF模型的因子图

（2）数据关联的能量

数据关联通常是多目标跟踪最有挑战性的一个方面。本文通过多标号CRF模型来阐述数据关联问题。连接时间邻域（ld,ld’）∈ƐS，ld与ld’表示相邻两帧具有相同标号的观测。该时间平滑边的能量定义如公式（15）所示：

其中δ（.）表示冲激序列，当ld≠lD’时，则产生一定的惩罚 λƐs。

为了防止数据误读，本文引入空间互斥边（d,d’）∈ƐX确保同一帧图像中每个目标的标号唯一，空间互斥边ƐX的能量定义如公式（16）所示：

其中δ（.）表示冲激序列。同一帧图像中，如果相邻目标之间的标号相同，则进行一定的惩罚。

2 离散与连续优化

本文旨在确定每个目标的标号，并确定每个目标的最优轨迹。为了能够找到公式（1）的强局部最小能量，本文采用离散-连续交替的优化方案来求取目标函数的最小能量。当离散标号的分配发生收敛时（或者迭代次数达到最大），优化步骤停止。接下来对每个部分的优化步骤进行详细介绍。

2.1 离散标号优化

离散优化旨在寻找一组带有标号l的目标，并把每个目标分配给唯一的轨迹(来自大量的轨迹假设池)。本文试图寻找一种方法求解等式(12)的最小能量。然而，等式(12)的二元互斥函数EdX（ld,ld’）为非子模函数；其次，Etr（Ti）引入的全局因子依赖于所有的标号，同时还需要采用一种恰当的方法求解二元标号能量EtrX（Ti,Tj） 。为了最小化标号成本，本文采用α-expansion算法，即把离散多标号问题转化为只有两个标号状态的问题进行求解。

由于 Ed（ld,T）、ES（ld,ld’）以及 EdX（ld,ld’）的能量很容易通过标准的α-expansion算法求得，因此本文重点描述Etr（Ti）与EtrX（Ti,Tj）的能量。假设我们已经通过恰当的方法获得标号集l，在求取能量的过程中，通过验证标号l是否会切换成α来确定其有效性，图中的Sα为辅助节点，用来表示标号的切换情况。这是一种只有两个状态的优化问题，其中0表示对应的标号不发生改变，1表示对应的标号l切换为标号α。

如图4所示，图4(a)中的δ节点产生的能量用Ed（ld,T）表示，只要δ节点的标号变为α，则产生成本L0，否则成本为0。图中的紫色与红色方形节点表示Es（ld,ld’）以及EdX（ld,ld’）产生的能量，即当同一帧图像中出现两个相同的标号，或者相邻两帧图像中由时间平滑边ƐS相连的标号发生切换时产生的能量。由于此时能量相对较大，可被视为无穷大。

图4 α-expansion算法示意图

单个轨迹的成本Etr（Ti）。为了确保只有一半的重叠轨迹被压缩，因此只在每一对具有相同物理空间的成对轨迹进行惩罚。然而，如何确定哪一个轨迹被惩罚是一个很重要的问题。为了解决该问题，本文采用了基于贪婪标号移除的α-expansion算法，即通过依次全部移除某个标号来检查能量是否进一步降低。由于能量函数为非子模函数，本文采用伪布尔函数多项式优化算法（QPBO）算法进行每一步α-expansion，对应的因子图如图4（b）所示。对于单个轨迹的成本Etr（Ti），图4（b）中黄色正方形表示目标β的标号切换为γ时产生的成本，记为L×。为了抑制两个不可能同时存在的标号而导致能量的增加，当且仅当两个对应的辅助变量同时发生标号切换时，则进行相应的惩罚L××，此时表示两个不同的目标β和γ同时切换为标号α。通过这种方式获得的是超子模函数的成本，而等式（12）的成本函数总体上是非子模的。

2.2 连续轨迹优化

由于能量函数的连续部分为非凸函数，但可以通过梯度下降法来进行求解，本文采用梯度下降法（BFGS）。最终的优化结果依赖于初始化轨迹。因此，本文采用连续能量全局最小化函数来表示，如公式（17）所示：

该等式除了Ed’项中的二次惩罚函数Dis(d,d’)=║x-y║2不一样，其他数据成本等同于上文的式(3)。于是等式（17）就转化成通过闭合形式求解的加权最小二乘问题，本文采用El×(T)轨迹作为初始化条件。

3 轨迹假设空间

本文采用采用改进的随机采样一致性算法（RandomSampleConsensus）拟合直线，优先检测那些在空间上和时间上更接近的轨迹，并随机选择观测子集。

仅仅依赖于初始的轨迹假设，可能会在一定程度上限制能量的最优解。为了使得优化的过程更加灵活，因此在基于当前解决方案的基础上，在每一次连续优化迭代结束之后，对轨迹假设的搜索空间进行一定的扩展。本文采用以下3种方法进行扩展轨迹假设空间：（1）对于那些连续超过10帧都没有检测到目标的轨迹，则把它分割成两个较短的轨迹。对于时间间隔不超过t0帧的轨迹片段i与j，则合并成一个新的轨迹，t0可以根据实际情况进行调整，本文t0=25。（2）如果迭代过程中有一两帧突然出现能量上升，短时间内又恢复正常，则认为当前帧是不可靠的，进一步从场景中移出移除这一帧轨迹。在若干次迭代以后，当新添加轨迹的能量仍然按梯度下降的方向进行，则说明新添加的轨迹比较可靠。（3）及时扩展现有轨迹，即通过移动轨迹的端点（si往前移动，ei向后移动）；或者及时收缩那些没有目标出现的轨迹，即分别移除原来轨迹端点处的前4帧和后4帧。轨迹假设空间的扩展过程如图5所示。

图5 扩展轨迹假设空间示意图

4 实验结果

4.1 参数设置

本文对每个参数进行固定调试。轮流固定公式1中β、γ、δ的值，改变另一个变量，判断对MOTA性能的影响。并根据MOTA指标进行适当调试，其余的两个参数值同理可得，为了方便调试，β固定为1，图6给出了其余两种情况下的评估标准。

图6 各参数的变化对MOTA指标的影响图

其中，参数β=1保持不变，分别先固定其他参数值，然后给出单个参数值改变时的影响。图6中每条曲线均表示MOTA随参数变化的情况。

从图6可以得出，某一调节系数的值变化较大时，只要跟踪结果的MOTA变化不是太大，则均认为该参数是可信的。当MOTA=0时，说明参数的变化对MOTA指标的影响很小。能量函数中的调节在以上4个数据集中，均设置为｛1, 0.03, 0.8｝。

另外，本文还给出了8种相关的参数，通过梯度下降法得到了最高平均MOTA值，表1为具体的参数值。

表1 相关参数值对应表

轮流的改变每个参数的值，取值范围从0到2，然后再与它们的标准值1相乘，并观察MOTA性能指标的变化。本文分别先固定其他参数值，然后给出单个参数值改变时的影响，所有参数被分成两组。

图7给出了第一组（λreg，λang，λEdX，λEs）参数的变化对整体MOTA性能指标的影响，从图中可以看出，跟踪精确度只出现了微小的变化，跟踪结果的鲁棒性较好。需要注意的是，不同的测试视频序列或者训练集，参数的重要性可能发生一定的变化。

图7 第一组参数变化对整体跟踪性能的影响图

图8给出了另一组相关参数（λper，λɸ，λEtrX，λlin）。当各自的能量权重下降时，MOTA性能指标受到了很大的影响。因此，有必要把误标号成本λɸ（离群值）、二元标号成本λEtrX以及轨迹持久性成本λper等相关参数考虑在内。其中λɸ参数是用来惩罚没有观测目标的平凡解。λEtrX防止来自同一个目标的观测被分配给不同的轨迹，从而减少误跟踪的数量。λper确保产生长久的、连续的目标轨迹，减少目标之间的身份切换（IDs）。

图8 第一组参数变化对整体跟踪性能的影响图

4.2 数据集

PETS2009benchmark数据集场景丰富、光照变化较强以及行人姿态变化各异，逐渐成为多目标跟踪实验最受欢迎的数据集之一。本文实验只使用其中部分的视频序列，由3个可用摄像机校准的视频序列组成。除了广泛使用的PETS2L1视频序列，还包括2个更具有挑战性的场景：S2L2以及S1L1-2视频序列。其中S2L1包含8个场景，共有795帧，8个行人，视频序列的分辨率为768×576；S2L2与S1L1-2视频序列随着时间的推移，场景中的行人越来越多，而且场景比较拥挤。其中S1L1-2共有240帧，S2L2共有435帧，视频图像序列的分辨率均为768×576。在所有实验中只使用第一摄像机视点。TUD-Stadtmitt行人数据集是采用低角度摄像机拍摄的行人街道，该数据集的视频序列共有250帧，图像分辨率为720×576。

4.3 评估指标

本文着重算法的鲁棒性和跟踪结果的准确性，对目标检测和跟踪性能进行评估。性能评估指标包含以下几方面：

（1）MOTA：目标跟踪准确度；

（2）MOTP：目标跟踪精确度；

（3）FAF：每帧中目标误警的数目；

（4）GT：实际的跟踪轨迹数目；

（5）MT：绝大多数正确跟踪的轨迹数目，正确跟踪的轨迹数目与实际的跟踪轨迹数目的百分比大于80%；

（6）ML：最大丢失的跟踪轨迹数目，丢失的跟踪轨迹数与实际的跟踪轨迹数目之比小于20%；

（7）Frag：跟踪过程中，轨迹发生中断的次数；

（8）IDs：跟踪轨迹中，目标身份交换的次数。

4.4 对比实验及分析

本文给出了PETS2009S2L1视频序列中的对比实验结果，包含8个运动目标，共有795帧图像，每一帧图像的间隔为0.01s。并选出第306帧、319帧和330帧的跟踪图像进行效果对比。

结合表2的实验数据可知，基于SegTrack跟踪算法在第306帧与319帧之间、第319帧与第330帧之间均出现了不同程度的漏检和标签互换。由于第306帧中的18号目标比较拥挤，到了第319帧中标签互换为48号，第319帧中的32目标在第306帧中出现了漏检。另外，第33号目标旁边的行人始终处于漏检状态。由于第319帧中的29号目标被物体遮挡，到了第330帧变成了52号目标。因此，该算法的跟踪性能并不是十分稳定。对于HDA-DVM算法，同样出现了不同程度的漏检问题。第306帧中的15号目标由于遮挡原因，到了第319帧出现了漏检；第319帧中的13号目标到了第330帧出现了漏检情况，而本文所提算法成功克服了由于遮挡、拥挤造成的漏检和标签互换问题。从表2的实验数据也可以看出，本文所提算法的精确度与准确度都要明显高于其他两种方法，而且在最大跟踪轨迹数MT指标也优于其他两种算法。

表2 三种跟踪算法跟踪性能对比结果表

5 结论

本文提出了一种基于数据关联与轨迹评估的多目标跟踪方法。首先，从时间和空间的角度建立CRF模型，并给出标号方式；其次，将目标的数据关联与轨迹评估整合到同一个CRF模型中，并详细地介绍了各个能量分量的模型；最后，采用基于贪婪标号移除的ɑ-expansion算法更新标号，以及基于梯度下降法的轨迹优化，并扩展了轨迹假设的空间。最后的实验结果表明，本文所提算法优于当前先进水平的多目标跟踪技术。