系统极化码低复杂度编码优化方案

马林华，刘士平，胡星，黄天宇，徐彬



系统极化码低复杂度编码优化方案

马林华1,2，刘士平1，胡星1，黄天宇1，徐彬3

（1. 空军工程大学航空工程学院，陕西 西安 710038；2. 西安电子科技大学综合业务网国家重点实验室，陕西 西安 710071；3.空军航空大学初级训练基地，黑龙江 哈尔滨 150100）

为解决系统极化码在编码过程中因分步计算造成的时延和由循环迭代“异或”计算造成的计算复杂度，提出并定义了降维裂解策略，并由此提出了基于降维裂解策略的系统极化码并行编码算法，然后在AWGN信道下进行了仿真验证和计算复杂度分析。结果表明，与传统算法相比，所提算法编码增益略优或基本保持一致，但计算复杂度优化率最高可达80.92%，更适合于硬件实现与工程应用，具有一定的实用价值。

极化码；系统极化码；并行编码；复杂度；裂解；误码率

1 引言

信道纠错编码技术是提高数字通信系统抗干扰能力的关键技术之一。香农在有噪信道编码理论中指出，存在可以达到香农限的码字[1]。自2008年土耳其教授Arican基于信道极化定理提出极化码（polar code）以来，极化码凭借低复杂度编译码以及信道容量可达的优势在信道编码领域占据重要地位，逐渐受到重视并开始应用于各个领域，拥有良好的发展前景[2-4]。

在编码理论中，系统码是输出码字包含输入信息序列的一类编码，即其信息比特会作为码字的一部分直接显现出来，而非系统码的输出码字中不包含输入信息序列。极化码的标准形式是非系统码，鉴于任意线性码都可以转换成系统码，因此，极化码也可被系统地编码[5]。研究表明，由于在译码时系统码的信息比特可以通过信道被直接观察，系统极化码相比于传统的非系统极化码具有更好的误比特率性能[5]，且信息位可直接在系统码码字中表现出来，即不需要通过冗长的译码过程就能得到合理的准确估计，可快速确定所接收源符号的正确性[6-7]。因此，系统极化码逐渐成为工程应用上的首选。

Arican[5]在首次提出系统极化码的同时也给出了该系统极化码的串行编码算法，文献[8]针对此算法进行了补充和复杂度分析。该算法将码字拆分成2个部分并按序依次进行嵌套运算，由于该运算机制随着码长的增加，会提高2个计算步骤之间的错误传播概率，并在2个计算步骤之间因等待造成系统时延。针对此问题，文献[9-10]提出一种并行计算的编码算法，利用双极化结构取代串行编码算法中分步计算的过程，可以实现任意码长、码率下对编码码字的一步直接计算。虽然此算法可以实现高度并行计算，降低因分步计算等待造成的时延及错误传播，但是由于增加了一个额外的极化结构导致“异或”运算的次数随着码长增加而呈指数级增长，提高了系统的计算复杂度，降低了编码效率，因此并没有从根本上解决系统运算时延问题[11]。基于上述问题，本文提出基于降维裂解策略的系统极化码并行编码算法，基于“分治法”的思想将整段码字裂解计算再合并，在保证可实时并行计算且不增加额外存储空间的同时，降低了计算复杂度及错误传播概率，更适用于硬件实现及实际应用。

2 系统极化码及背景算法描述

2.1 极化码与系统极化码

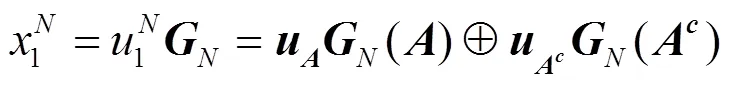
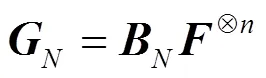
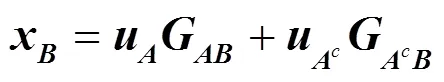
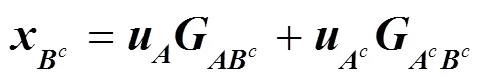
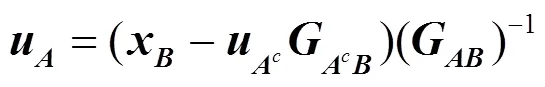
2.2 系统极化码并行编码

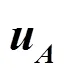
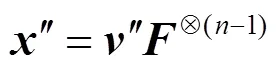
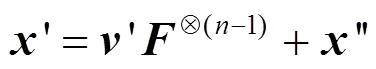
针对上述问题，文献[9]对此进行改进并提出了一种新型系统编码器，该编码器可以实现编码的并行计算，并可直接经过编码得到最终码字，避免中间步骤的等待时延。

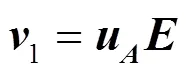
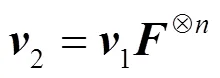
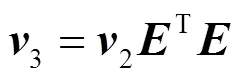
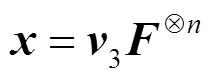
综合式(8)~式(11)，可以整合出生成码字计算式，即

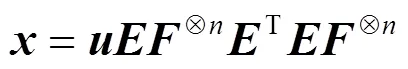
该并行编码算法的编码器结构如图1所示。由式(12)及图1可以看出，该编码算法将输入码字看作一个整体对编码过程完成“一步计算”，解决了系统极化码串行编码因分段计算造成的时延及错误传播问题。

3 降维裂解并行编码算法

3.1 降维裂解策略

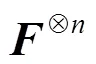
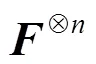
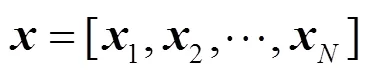
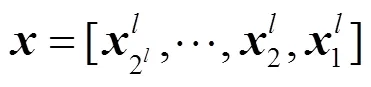
其中，元素表示码树第层第个子向量，,。可理解为类似于C语言中码字向量子向量的指针。定义偏移向量，与分别表示图2所示循环递归编码码树的层数及各层中向量的序号。根据裂解策略及编码码树观察可得出，第层的个向量长度均为，且每层的向量按顺序连接起来均为长度相同的码字向量，这也验证了上述定义的裂解算法的正确性。

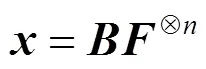
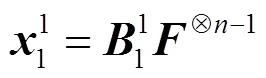
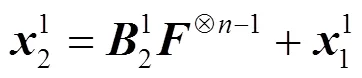
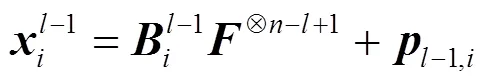
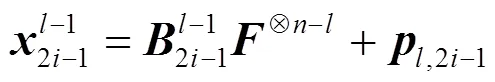
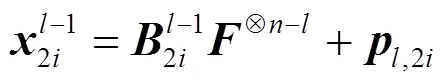
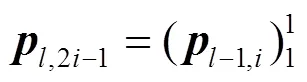
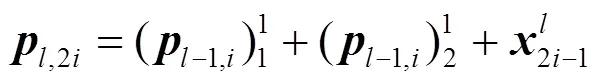
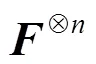
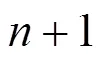
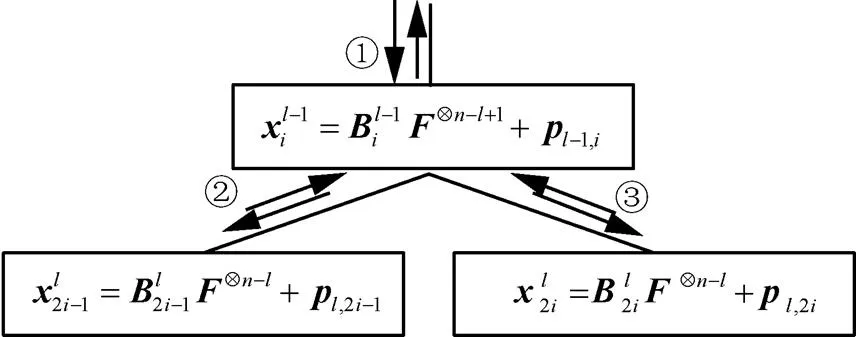
图3 循环迭代单元结构

第三次（③）：第三次也是最后一次返回该节点，此时已经遍历了整个子树并得到了式(17)的结果，最终返回父节点。

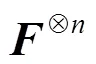
3.2 基于降维裂解策略的系统极化码并行编码

利用上述定义的降维裂解编码策略，在保留文献[8]中并行编码算法优点的基础上，对式(12)进一步做低复杂度优化，提出了系统极化码的降维裂解并行编码，具体算法描述如下。

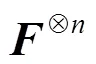
式(22)所表示的优化并行编码算法可具体阐述如下。

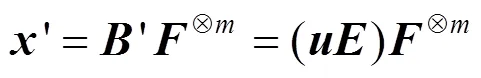
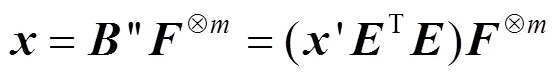
上述2个步骤（即式(23)和式(24)）是依次进行的，利用所提降维裂解策略对传统并行编码算法进行低复杂度优化，充分保留了传统并行算法“一步计算”降低错误传播的特点，最终得到基于降维裂解策略的并行编码。

4 仿真验证及复杂度分析

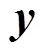
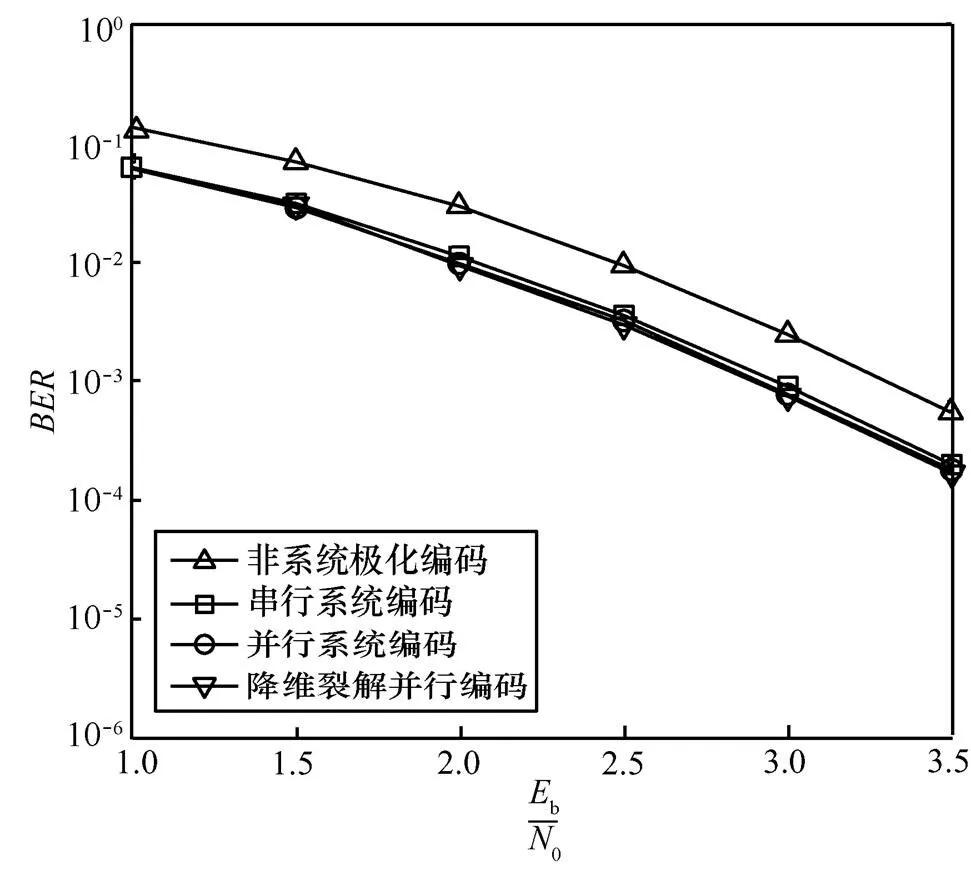
图4 （256,128）系统极化码不同编码算法性能对比

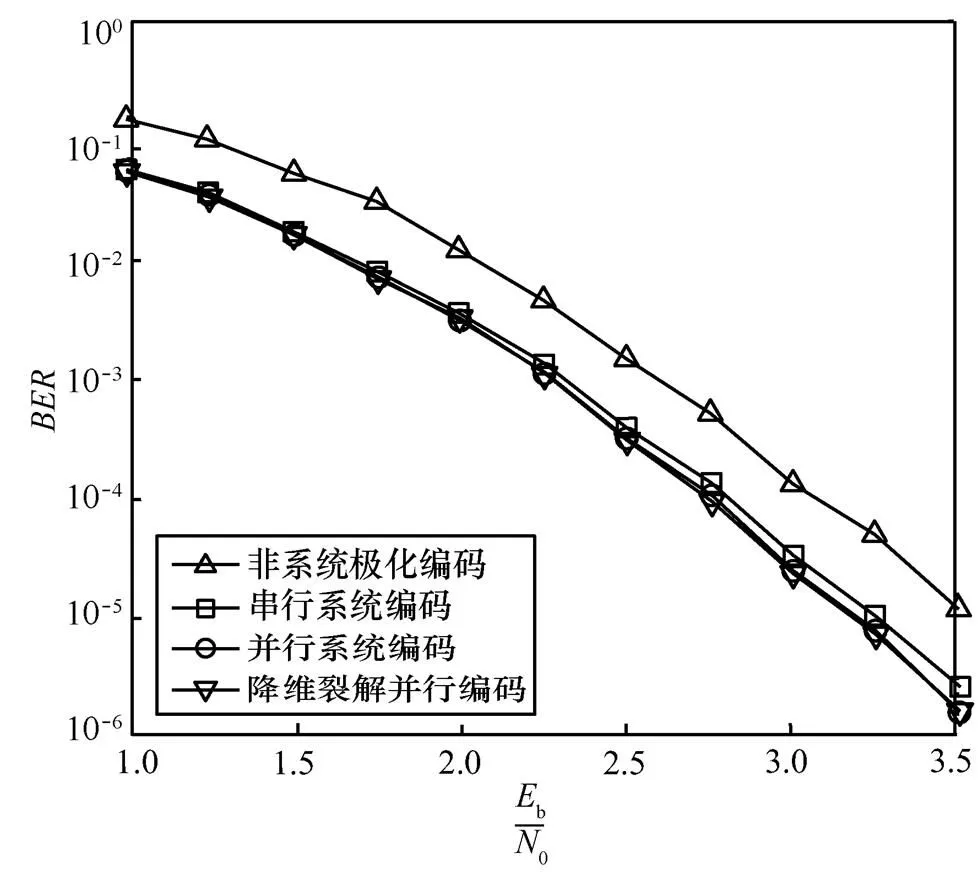
图5 （1 024,512）系统极化码不同编码算法性能对比

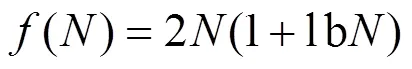
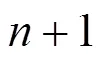
表1 系统极化码编码复杂度对比

表2 不同码长下本文算法与传统编码算法计算复杂度优化率对比

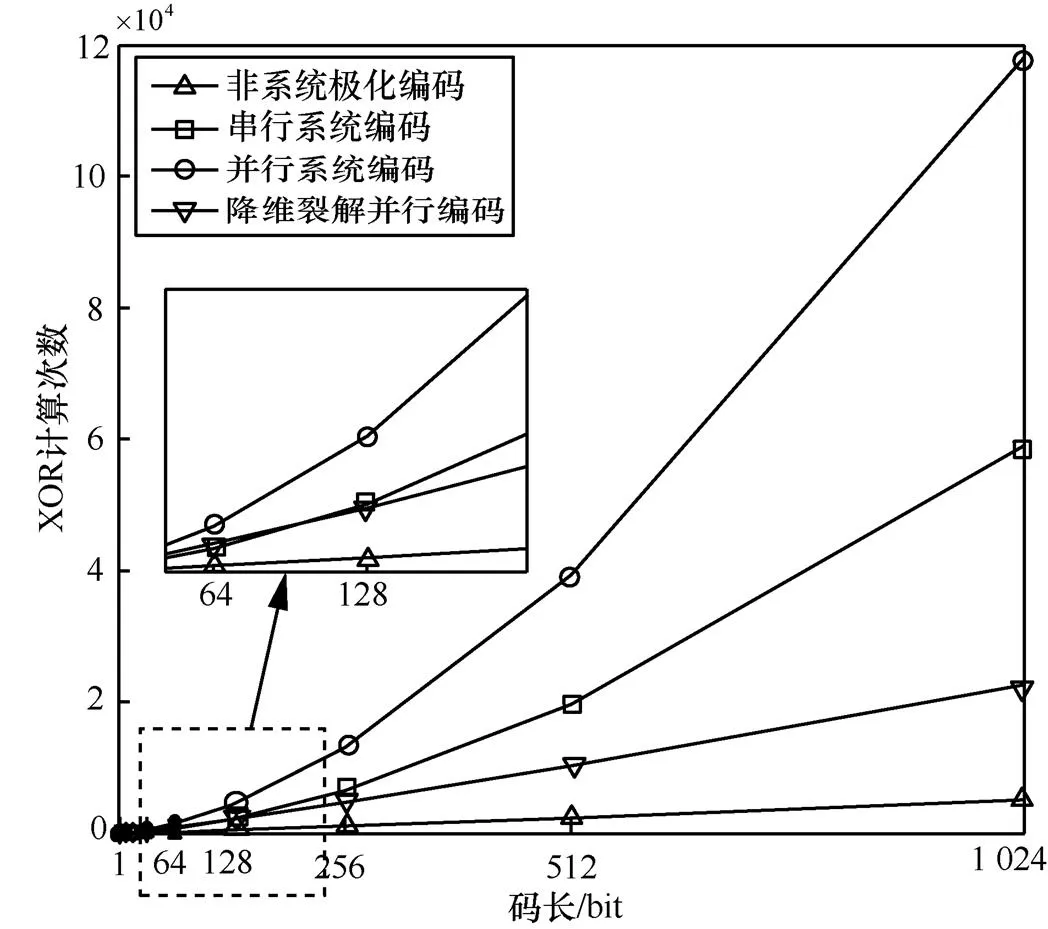
图6 不同编码算法复杂度变化趋势

上述仿真验证及复杂度分析表明，当码长128时，降维裂解算法的编码增益与并行系统编码基本一致，但是计算复杂度明显降低。相比于串行编码，无论是计算复杂度还是编码增益，都起到了优化的效果。当码长<128时，编码增益与上述类似，但计算复杂略高于串行系统编码。由于码长较短使计算复杂度提升并不明显，且编码增益优于串行编码，因此本文算法在任意码长下都可以发挥作用。

5 结束语

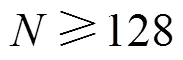
[1] SHANNON C E. A mathematical theory of communication[J]. Bell System Technical Journal, 1948, 19(4): 271-285.

[2] ARICAN E. Channel polarization: a method for constructing capacity achieving codes for symmetric binary-input memoryless channels[J]. IEEE Transactions on Information Theory, 2009, 55(7): 3051-3073.

[3] ARICAN E. A performance comparison of polar codes and reed- muller codes[J]. IEEE Communications Letters, 2008, 12(6): 447-449.

[4] ARICAN E. Channel combining and splitting for cutoff rate improvement[J]. IEEE Transactions on Information Theory, 2006, 52(2): 628-639.

[5] ARICAN E. Systematic polar coding[J]. IEEE Communications Letters, 2011, 8(15): 860-862.

[6] FENG B, ZHANG Q, JIAO J. An efficient rateless scheme based on the extendibility of systematic polar codes[J]. IEEE Access, 2017, PP(99): 1.

[7] YOO H, PARK I C. Partially parallel encoder architecture for long polar codes[J]. IEEE Transactions on Circuits & Systems II Express Briefs, 2015, 62(3): 306-310.

[8] LI L, ZHANG W. On the encoding complexity of systematic polar codes[C]//IEEE International System-on-Chip Conference. 2015: 415-420.

[9] SARKIS G, TAL I, GIARD P, et al. Flexible and low-complexity encoding and decoding of systematic polar codes[J]. IEEE Transactions on Communications, 2016, 7(65): 2732-2745.

[10] SARKIS G, GIARD P, VARDY A, et al. Fast polar decoders: algorithm and implementation[J]. IEEE Journal on Selected Areas in Communications, 2014, 32(5): 946-957.

[11] TAL I, VARDY A. How to construct polar codes[J]. IEEE Transactions on Information Theory, 2011, 59(10): 6562-6582.

[12] RICHARDSON T J, SHOKROLLAHI M A, URBANKE R. Design of capacity-approaching irregular low-density parity-check codes [J]. IEEE Transaction on Information Theory, 2001, 47(2): 619-637.

[13] CHUNG S Y, RICHARDISON T J, URBANKE R. Analysis of sum-product decoding of low-density parity-check codes using a gaussian approximation[J]. IEEE Transactions on Information Theory, 2001, 47(2): 657-670.

[14] ZHANG Z Y, ZHANG L, WANG X B, et al. A split-reduced successive cancellation list decoder for polar codes[J]. IEEE Journal on Selected Areas in communications, 2016, 34(2): 292-302.

[15] BALATSOUKAS-STIMMING A, RAYMOND A J, GROSS W J, et al. Hardware architecture for list successive cancellation decoding of polar codes[J]. IEEE Transactions on Circuits & Systems II Express Briefs, 2014, 61(8): 609-613.

Optimizing low complexity encoding method for systematic polar code

MA Linhua1,2, LIU Shiping1, HU Xing1, HUANG Tianyu1, XU Bin3

1. Aeronautics and Astronautics Engineering College, Air Force Engineering University, Xi’an 710038, China 2. The State Key Laboratory of Integrated Services Networks, Xidian University, Xi’an 710071, China 3. Air Force Aviation University Primary Training Base, Harbin 150100, China

In order to solve the delay caused by step-by-step calculation and the computational complexity caused by iterative “exclusive-or” computation during the encoding process, a dimensionality reduction strategy was proposed and defined. Based on this, system polarization code parallel coding algorithm for cracking strategy was proposed. Simulation and computational complexity analysis were carried out on AWGN channel. The results show that the coding gain of the above algorithm is slightly better than the traditional one or almost the same, but the computational complexity is up to 80.92%, which is more suitable for hardware implementation and engineering application. It is more suitable for hardware implementation and has a certain practical value.

polar code, systematic polar code, parallel encoding, complexity, splitting decomposition, bit error rate

TN911.22

A

10.11959/j.issn.1000−436x.2018127

2018−01−11；

2018−05−19

国家自然科学基金资助项目（No.61472442）；陕西省科技攻关基金资助项目（No.2017GY-049）；航空科学基金资助项目（No.20155896025）

The National Natural Science Foundation of China (No.61472442), Shaanxi Province Scientific and Technological Project (No.2017GY-049), Aviation Science Foundation (No.20155896025)

马林华（1965−），男，陕西汉中人，博士，空军工程大学教授、博士生导师，主要研究方向为抗干扰通信、信道编码、无线自组织网络。

刘士平（1994−），男，黑龙江哈尔滨人，空军工程大学硕士生，主要研究方向为信道编码、极化码、抗干扰通信。

胡星（1990−），男，河南南阳人，空军工程大学博士生，主要研究方向为模拟量编码、卫星通信。

黄天宇（1993−），男，辽宁营口人，空军工程大学硕士生，主要研究方向为Massive MIMO下行传输技术及信道仿真器设计。

徐彬（1993−），男，吉林吉林人，空军航空大学工程师，主要研究方向为信道编码、抗干扰通信。