Spherical Gravitational Collapse in f(R)Gravity with Linear Equation of State

Zahid Ahmad, Hassan Shah, and Suhail Khan

1Department of Mathematics,COMSATS Institute of Information Technology,University Road,Post Code 22060,Abbottabad,KPK,Pakistan

2Department of Mathematics,University of Peshawar,Peshawar Khyber Pukhtoonkhwa,Pakistan

AbstractIn a paper[Gen.Relativ.Gravit.48(2016)57]Chakrabarti and Banerjee investigated perfect fluid collapse in f(R)gravity model and claimed that such a collapse is possible.In this paper we show that without the assumption of dark energy it is not possible that perfect fluid spherical gravitational collapse will occur.We have solved the field equations by assuming linear equation of state(p= ωµ)in metric f(R)gravity with ω = −1.It is shown that Chakrabarti and Banerjee reached to false conclusion as they derived wrong field equations.We have also discussed formation of apparent horizon and singularity.

Key words:gravitational collapse,matching conditions,dark energy,apparent horizon

1 Introduction

It is well known that our universe is expanding at an accelerated rate[1−2]and the suspected reason behind this expansion is dark energy.To study dark energy problem two different approaches have been developed.One approach is to develop different dark energy candidates and the other is to modify the theory of general relativity.There are different theories of modified gravity,which generalizes in some way the theory of general relativity,for example,Brans-Dick theory,string theory,modified Gauss-Bonnet theory,f(T)theory,f(R,T)theory and f(R)theory of gravity.All these modifications of the general theory of relativity enable us to investigate the dark energy problem in a systematic way.[3−5]The very natural gravitational alternative for dark energy is the f(R)theory of gravity.[6]Moreover this theory is useful in the unification of early time inflation and late time acceleration.

In order to analyze the dark energy of our present universe,one can utilize the equation of state parameter(EoS) ω.The universe passes through Λ-Cold Dark Matter(ΛCDM)epoch,when the EoS parameter is equal to−1.If the EoS parameter is less than−1 then the universe enters in the phantom phase.When the EoS parameter is greater than−1 then the quintessence dark era occurs.[6]In recent past,many researchers did notable work on the gravitational collapse of dark energy in general relativity as well as in modified theories of gravity.Cai and Wang[7]discussed collapsing dust fluid model of dark energy with isotropic pressure in general relativity by taking spherical geometry.Ahmad and Shah[8]generalized this work for anisotropic pressure.Chakraborty and Bandyopadhyay[9]studied collapse dynamics of an inhomogeneous star of dark matter and dark energy with anisotropic pressure.Bhatti and Yousaf[10]discussed collapsing model of dark universe with Lemaitre-Tolman-Bondi(LTB)geometry in f(R)gravity.Sharif and Kauser[11]examined Bianchi type III model in f(R)gravity with anisotropic fluid.For more analysis of dark energy problem and modified theories,we refer the papers.[12−14]

Sharif and Kauser[15]investigated perfect fluid collapse in f(R)gravity by applying the constant curvature assumption,that is,R=R0.They concluded that the f(R0)term plays the role of positive cosmological constant.Shamir et al.[16]inspected collapsing dust model in f(R)theory by taking FRW and Schwarzschild spacetimes in the interior and exterior regions respectively.The work done by Shamir et al.[16]was extended by Ahmad and Khan[17]to(n+2)dimensions. Sharif and Nasir[18]discussed structure scalars in dissipative axial system in f(R)gravity.Kauser and Noureen[19]examined charged dissipative spherical collapse in f(R)gravity with anisotropic pressure.Sharif and Abbas[20]investigated dynamics of shear free collapse with radiating source in modified Gauss-Bonnet gravity theory by applying covariant gauge invariant perturbation approach with(3+1)formalism.

Lemaitre-Tolman-Bondi model is considered as a geometrical tool for describing non radiating and inhomogeneous matter with spherical geometry.[21]This model is widely used to study cosmological as well as quantum gravity problems.Keeping in mind the interesting features and wide range applications of LTB spacetime and the usefulness of f(R)gravity theory in the unification of early time inflation and late time acceleration,we are interested here to study perfect fluid collapse with linear equation of state by taking a special type LTB spacetime in the interior region and a general spherically symmetric spacetime in the exterior region.In particular we will consider Schwarzschild geometry in the exterior region.This paper contains five sections.In Sec.2,we have derived the field equations.Section 3 contains the solution of the filed equations by considering linear equation of state p=ωµwith ω = −1.In Sec.4,we derive the matching conditions.Apparent horizon is studied in Sec.5.In the final section,we summarize our results.

2f(R)Gravity and Field Equations

The field equations in f(R)gravity is given by[22]

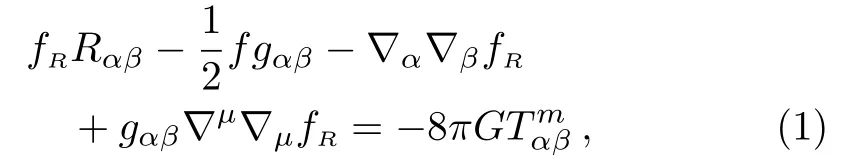
where fR=df/dR.We can write the above equation in the following form

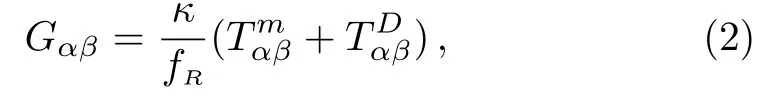
where

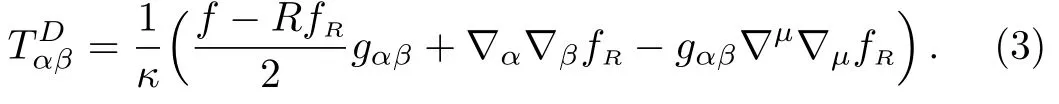
The Lemaitre-Tolman-Bondi(LTB)geometry is de fined as[21]

here W and Y are functions of t and r.Lemaitre-Tolman-Bondi model is considered as a geometrical tool for describing non radiating and inhomogeneous matter with spherical geometry.This model is widely used to study cosmological as well as quantum gravity problems.Here we consider a special type of the LTB spacetime with separable metric components as considered in Ref.[23]

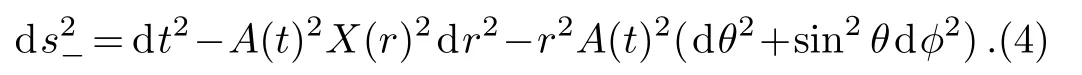
We consider that the energy momentum tensor in the interior of the star as follows

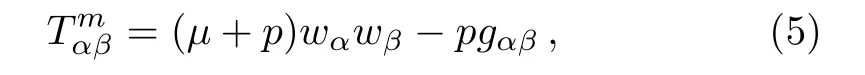
whereµis the energy density,p is the pressure,and wαis the four velocity vector satisfying the relation wαwα=1.In comoving coordinates,for the spacetime(4)we have

The field Eqs.(6),(7),and(8)in Ref.[23]are clearly wrong.The correct form of the field equations in terms of the current notations now become as:

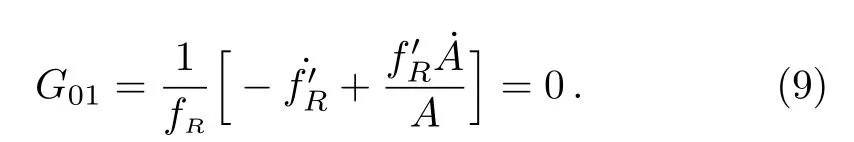
From Eq.(9),we have

Integrating Eq.(10)with respect to t,we get

where W0denotes arbitrary function of integration,which depends on r only.Integration of Eq.(11),with respect to r,yields

Now from Eqs.(6)–(8),we obtain

Substituting Eq.(12)in Eq.(13),we get

The above equation corresponds to Eq.(12)of Ref.[23].It can easily be seen that the third term on the left hand side in our Eq.(14)is missing in Ref.[23]and this is the reason that they solved their equation without the assumption of a linear equation of state p=ωµ with ω = −1.

3 Gravitational Collapse of Dark Energy

In this section,we assume linear equation of state p= ωµwith ω = −1 to discuss the collapse of dark energy.With this assumption Eq.(14)becomes:

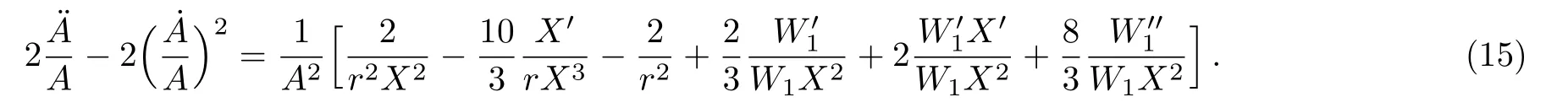
Now multiplying both sides of the above equation by A2,one can easily separate Eq.(15)into two parts,in which the left hand of side depends on t and the right hand of side depends on r only.Therefore we can set both sides equal to a constant.In this paper our aim is to study the time evolution of the collapsing model,therefore we only consider the time dependent part of Eq.(15),given by

where ξ denotes constant of separation and is non negative.The first integral of Eq.(16)yields

where η is integration constant.Since we are dealing with a collapsing process,therefore,we will take only non positive roots,i.e.,With this assumption we get the following analytic solution of Eq.(17)

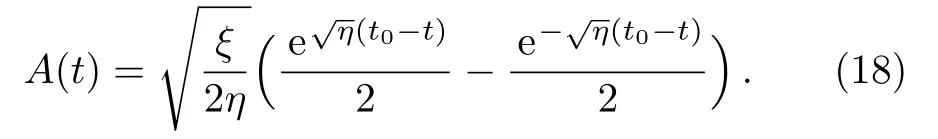
The relation between W1(r)and X(r)can be obtained from the r dependent part of Eq.(15)as

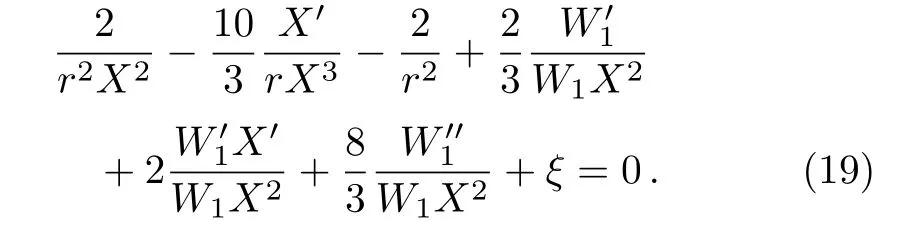
The total mass inside the radius r and time t can be calculated by using the mass function m(r,t)de fined by Cahill and McVittie[24]

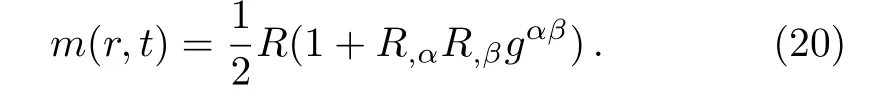
For metric(4),it becomes

Now using Eq.(17)in Eq.(21),we get

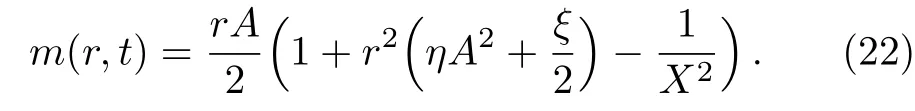
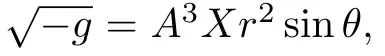
For the spacetime(4),Ricci scalar R takes the following form

The Kretschmann scalar,de fined as K=RαβγδRαβγδis used to investigate the singularity.[25]The derived value of the Kretschmann scalar in Ref.[29]is not correct.The correct value is obtained here as follows:

From Eqs.(23)and(24)it is evident that at t=tsboth the scalar goes to infinity whenConsequently this singularity is a curvature singularity.

4 Junction Conditions

This section is devoted to derive the junction conditions between the collapsing star with the exterior vacuum spacetime.First of all we will develop the junction conditions by taking a general spacetime in the exterior of the star and then for Schwarzschild spacetime as a specific case.We will use the junction conditions de fined by Israel-Darmois.[26]

Let the interior region of the star is denoted by N−and exterior vacuum region of the star by N+.In the interior region N−the metric is given by Eq.(4)while in the exterior region N+we take the metric in the following form[7]

The equation of Σ for the interior and exterior spacetimes are de fined as

respectively,where rΣis constant.Using Eqs.(26)and(27)in Eqs.(4)and(25),the continuity of the first fundamental formgives the following relations

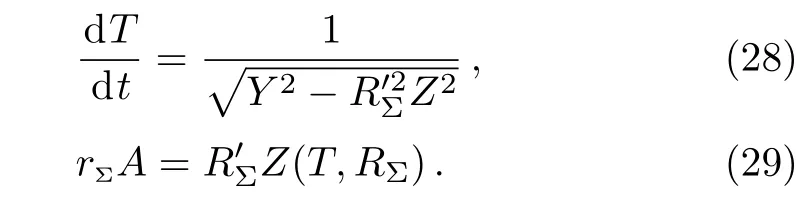
For Eqs.(4)and(25),the non vanishing extrinsic curvaturecomponents are given by

Hence the continuity of the second fundamental formgives

Specifically,if we take the Schwarzschild metric in the exterior vacuum region as:

with E(R)=1−2M/R,then we have by simple calculation that

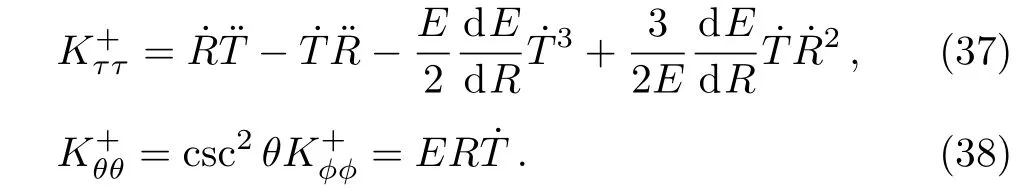
In this case,the continuity ofandover Σ,yields

where m(t,r)is given by Eq.(22)and M is the Schwarzschild mass.

5 Apparent Horizon

The apparent horizon is formed when the trapped surface is formed at which the outward normal is null and mathematically it is de fined as[21,27]

where Rpis the proper radius.The above condition for the spacetime(4).yields

It is clear from Eq.(4)that A depends on t and X depends on r,thus we can write

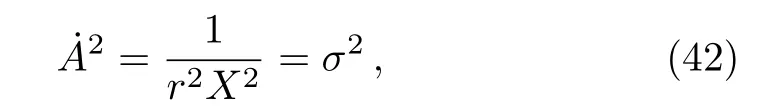
where σ is a constant.

One can find the time of formation of the apparent horizon by using Eqs.(17)and(42)as

The above expression shows that for σ2≥ ξ/2 apparent horizon will appear.Using Eq.(18),the time of appearance of singularity(A=0)is found as:

From Eqs.(43)and(44),the visibility of the central singularity is found as

From the above expression,we see that the singularity does not depend on the radial coordinate r,this type of singularity is non central and their occurrence is possible at all points simultaneously.According to Joshi et al.[28]in such a situation there is no probability of the appearance of naked singularity.

6 Conclusion

In this paper,we studied perfect fluid spherical gravitational collapse in f(R)theory of gravity by taking a metric whose metric functions are separable as multiplicative functions of radial and temporal coordinates.A simple analytic solution is obtained by assuming linear equation of state(p= ωµ)with ω = −1.Our study shows that without the assumption of dark energy it is not possible that a perfect fluid spherical gravitational collapse will take place.The earlier claim of Chakrabarti and Banerjee,[23]that such a gravitational collapse is possible without assuming dark energy,is shown here as false,because the basic Einstein’s field equations derived there are wrong.We derived the corrected field equations and solved them with the assumption of(p= ωµ)for ω = −1.

We found that the collapsing fluid crumples to a singularity of zero proper volume. The correct form of Kretschmann scalar is also obtained and it is shown that for this model a curvature singularity will form.It is shown that the apparent horizon formation depends upon ξ and σ,which are separation constants appearing in Eqs.(16)and(42)respectively.The condition for the appearance of apparent horizon is obtained as σ2≥ ξ/2.The difference between the time of appearance of singularity and the time of formation of the apparent horizon is also calculated and it is concluded that singularity does not depend on the radial coordinate r,and is thus non central,that is,it can take place at all points simultaneously.