Mass Spectra of Heavy and Light Mesons Using Asymptotic Iteration Method

Richa Rani,S.B.Bhardwaj,and Fakir Chand

Department of Physics,Kurukshetra University,Kurukshetra-136119,India

AbstractThe non-relativistic radial Schrödinger equation is analytically solved using asymptotic iteration method within the framework of a general interaction potential whose special cases are the Cornell and Cornell plus harmonic potentials.The energy eigenvalues expression is derived in three dimensional space,which is further used to calculate the mass spectra of mesons.The obtained results of this work are in good agreement with experimental and other relativistic results and also improved in comparison with other non-relativistic recent studies.

Key words:Schrödinger equation,asymptotic iteration method,mass spectra,mesons

1 Introduction

The quarkonium mass spectra can be understood theoretically via two different approaches. The first one is a direct calculation using quantum chromodynamics(QCD).[1−2]These calculations can be done with lattice QCD,but are complex and computationally very expensive.The other technique is the use of potential models to describe the bound states,which is similar to the description of energy levels in quantum mechanical systems.The experimentally observed mass spectra of the quarkonium system can be reproduced with a simple potential model by the use of an interaction potential in non-relativistic quantum mechanics.In this approach,the potential V(r)is taken as a function of the relative separation r between a quark and an anti-quark and the problem is then handled mathematically by solving the time independent Schrödinger equation(SE)for V(r).Mostly the inter quark potential is represented by the Cornell potential,

Eichten et al.[3]obtained the mass spectra ofmeson within the framework of non-relativistic quantum mechanics using four types of interaction potentials i.e.QCD motivated potential,power law potential,logarithmic and Cornell potentials and also showed the radiative decays of excited states ofmeson.Gupta et al.[4]calculated the mass spectra of mesons using Cornell potential by solving the non-relativistic SE numerically.Hassanabadi et al.obtained the wave function of mesons by solving the Klein-Gordon equation with Cornell interaction between mesons[5]and also calculated[6]the masses and wave functions of heavy baryons by solving the radial SE using perturbation theory.Hassanabadi et al.[7]solved the radial SE using variational method and studied the properties of light and heavy mesons by considering Cornell interaction.Ebert et al.[8]studied mass spectra and radiative decay rates of charmoniun,bottomonium andmesons using relativistic quark model based on quasipotential approach.

Wong[9]calculated the dissociation temperature of heavy quarkonia using temperature dependent Yukawa potential inferred from lattice gauge calculations.Shady[10−11]analytically solved the N-dimensional radial SE using Nikiforov-Uvarov method and obtained the mass spectra of charmonium and bottomonium using Cornell and Cornell plus harmonic potentials.Kumar et al.obtained the mass spectra of heavy mesons by considering Cornell plus harmonic(Coulomb perturbed)interaction between mesons by solving N-dimensional radial SE using power series[12]and asymptotic iteration methods(AIM).[13]They also solved the SE using Hill-determinant method and obtained energy spectra of a two electron quantum dot in a magnetic field.[14]

With a view to generate improved results for quarkantiquark systems here,in the present work,we consider a general interaction potential

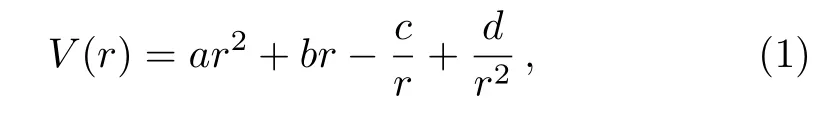
where a,b,c and d are positive potential parameters,which will be fixed by considering experimental data later on.The additional term d/r2to Cornell plus harmonic(CpH)potential improves the behavior of potential in the region r→0 i.e.it provides better confinement and leads to improved results as compared to CpH potential.[13]

The other important interaction potentials like Cornell and Cornell plus harmonic potentials are special cases of potential(1).This potential has also been used to investigate the energy eigenvalues spectra of quantum dot systems[15−16]and we also successfully applied the same potential to calculate bound energy states of a number of diatomic molecules.[17]Recently Khokha et al.[18]analytically determined the mass spectra of mesons by solving the N-dimensional radial SE using exact iteration method with the potential(V(r)=ar2+br−c/r−d/r2),which may be regarded as a variant of potential(1)and many more studies on mesons are reported in Refs.[19–25].

In literature there exist a number of exact and approximate analytical methods to solve the SE for such interaction potentials.Here,however,we prefer the AIM,relatively simpler and direct one,to calculate the mass spectra of light and heavy mesons.In fact,this method generates lesser constraing relations among potential parameters as compared to power series method.[12]

The paper is organized as follows:In Sec.2,we obtain an analytical expression for energy eigenvalues spectra for the interaction potential(1)employing AIM.In Sec.3,we apply the results to the quarkonium system to obtain their mass spectra and compare results with the experimental data.Finally,concluding remarks are given in Sec.4.

2 Mathematical Formalism

In this section, firstly,in brief,we briefly discuss the AIM,which is a technique to solve second order differential equations of the form

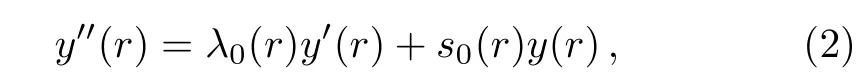
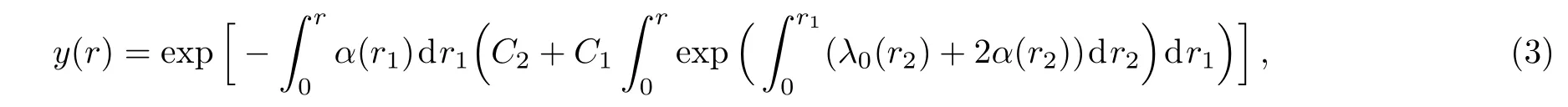
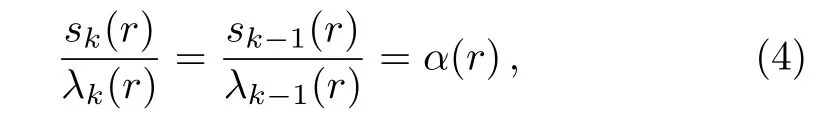
where

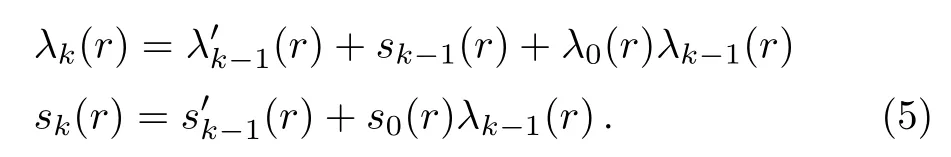
Thus,in order to find the solutions of the SE for a given potential, firstly we convert the SE into the form of Eq.(2)and then for given s0(r)and λ0(r),determine sk(r)and λk(r)parameters using the recurrence relation(5).

By using Eq.(4),the termination condition can be written as

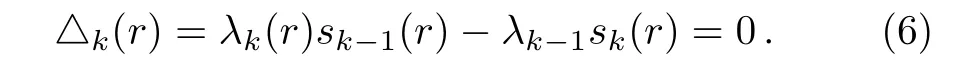
Note that the roots of the above equation provide the energy eigenvalues for the exactly solvable problems.But for other cases,for a particular principle quantum number n,one can choose a suitable r0point,which is generally determined as the maximum value of the asymptotic wavefunction or the minimum value of the potential,and then the approximate energy eigenvalues are obtained from the roots of this equation for sufficiently large value of k iteratively.

Now,consider the three-dimensional radial SE(~=1)for the interaction potential(1)as

where l=0,1,2,...denotes the angular momentum quantum number,µis the reduced mass of the system,which contains particles of masses m1and m2i.e.µ=m1m2/(m1+m2)and E are the energy eigenvalues corresponding to the radial wave function ψ(r).

On substituting ψ(r)=(1/r)R(r)into Eq.(7),we get

Further,make the following ansatz for the radial wave function R(r)as

where α and β are positive parameters whose values are to be determined later in terms of potential parameters.

Inserting Eq.(9)into Eq.(8),we obtain

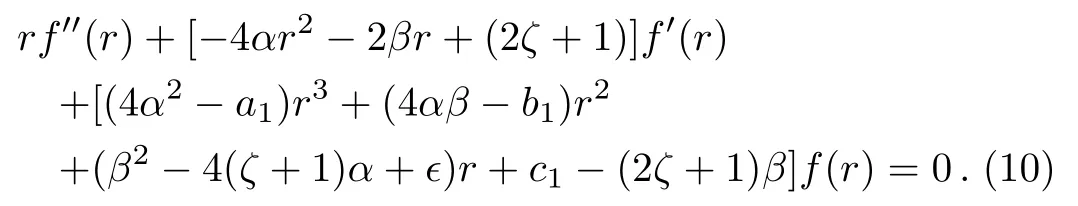
For the ground state,take f(r)=1,then Eq.(10)reduces to

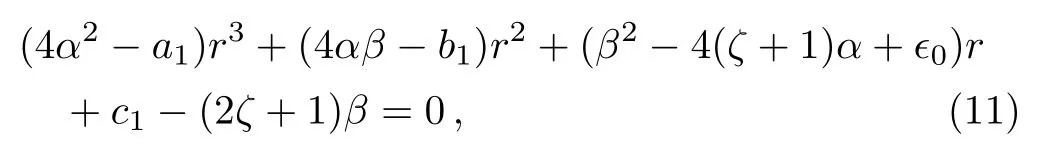
By equating each coefficients of r to zero in Eq.(11),we get the following equations

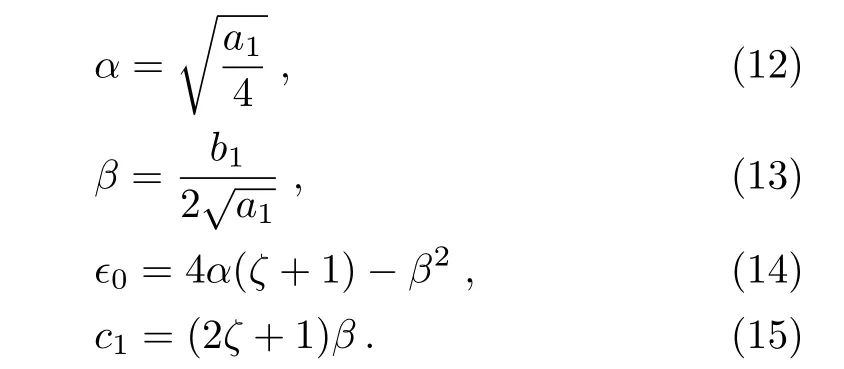
Finally,the ground state energy eigenvalues equation,after using Eqs.(12)–(14)is written as

45.You have passed sentence on yourself; and even so it shall be done to you: Full justice is served by having the maid choose her own punishment. According to Bettelheim, the message is that evil intentions are the evil person s own undoing107 (Bettelheim 1975, 141). Return to place in story.

Note that Eq.(15)leads to following constraint relation on the choice of potential parameter c

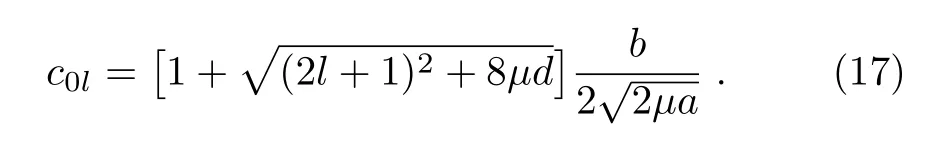
Now in order to determine the complete eigenvalues spectra of the considered system,we find the asymptotic solutions i.e.for r→∞and r→0 of Eq.(10).Therefore,Eq.(10)can be re-written using Eq.(11)as

where δϵn= ϵn− ϵ0.

Now firstly,we determine the solutions of Eq.(18)for large values of r i.e.r→ ∞.Under this limiting case,Eq.(18)becomes

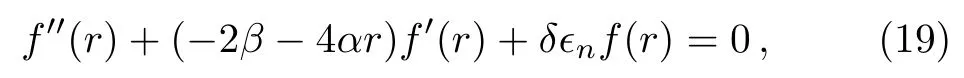
Comparing Eq.(19)with Eq.(2)and using recursion relation(5),one obtains the following expressions

Substitution of above values into Eq.(6),gives us

Secondly,we find the solutions of Eq.(18)for small values of r i.e.r→0.Equation(18)under this limit then becomes

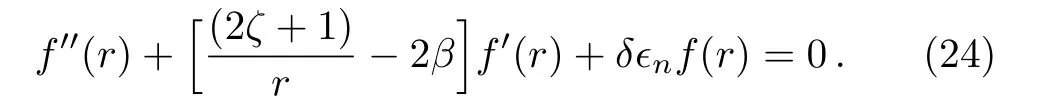
Again comparing Eq.(24)with Eq.(2)and using recursion relation(5),we obtain

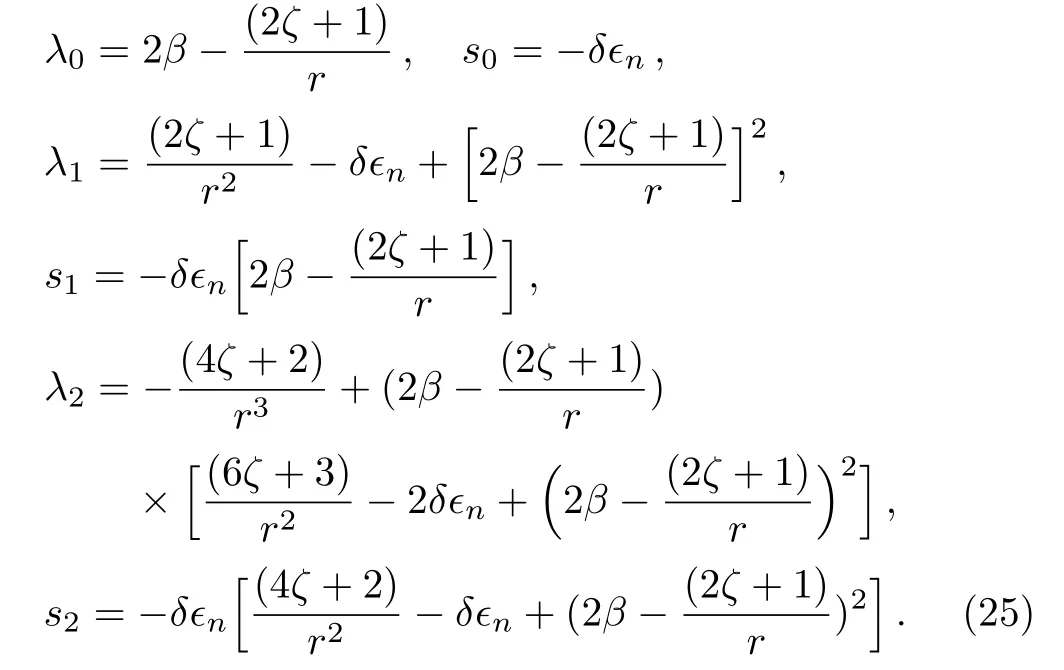
For these values of parameters,the termination condition given by Eq.(6)is not exactly solvable.Therefore,we find the root of equation λ0(r)=0 i.e.r=(ζ+1/2)/β,which is minimum value of the potential.For this minimum value of potential,Eq.(6)provides us

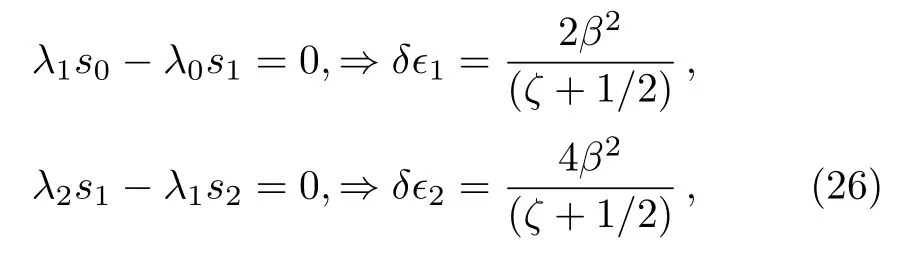
and so on.Thus,from these above values,we get

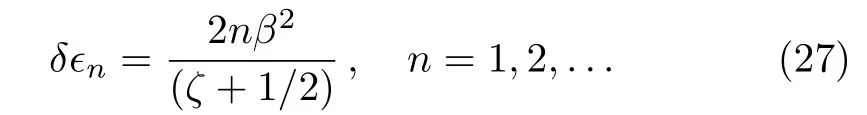
Finally,the complete spectra of potential(1)is obtained from Eqs.(23)and(27)as

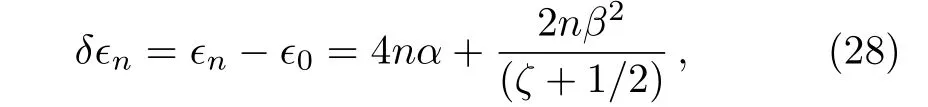
and the energy eigenvalues equation becomes

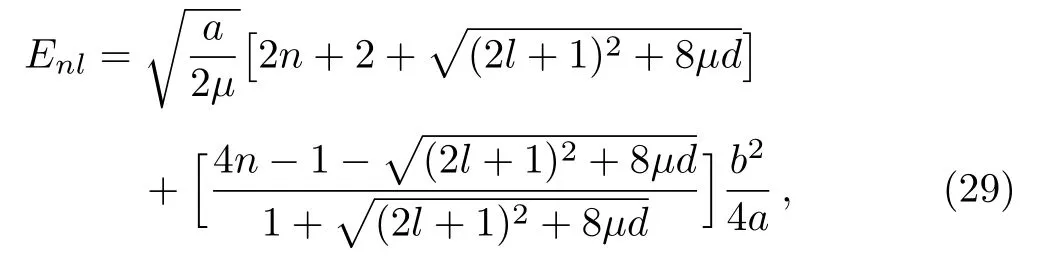
with the restriction on c as

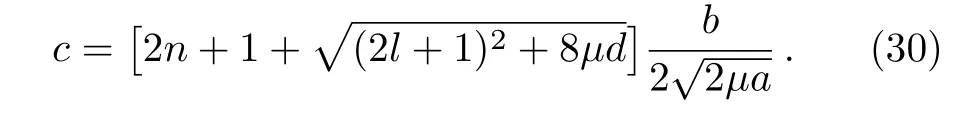
3 Mass Spectra of Mesons

Here,in this section,we obtain the mass spectra of heavy and light mesons by using the relation[27−28]

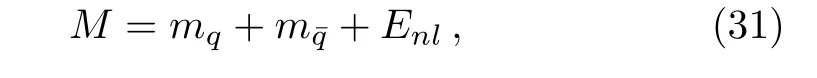
where mqandare quark and antiquark masses.

In the light of Eq.(29),above equation becomes

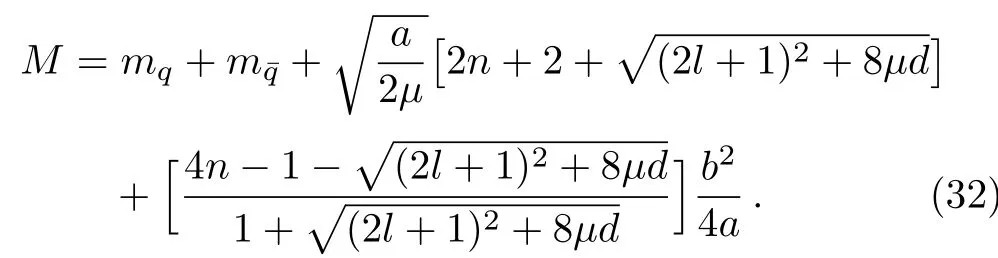
In literature,the masses of charm and bottom quarks are taken between 1.2 GeV to 1.8 GeV and 4.8 GeV to 5.3 GeV respectively.[6,8,18,29−31]In this work,we have chosen mc=1.209 GeV,mb=4.823 GeV,ms=0.419 GeV,and md=mu=0.220 GeV.[32−34]

The potential parameters a,b,and d for various mesons are determined using Eq.(32).In case of charmonium,the values of a,b,and d are calculated by solving three algebraic equations in a,b,and d,which are obtained by inserting experimental values of M for 1S,2S and 2P states(see*values in Table 1)in Eq.(32).In bottomonium case,we first fixed the value of d as calculated in case of charmonium and then determined a and b again using experimental values of M for 1S and 2S states from Table 2.For the case of,b,and d are fixed as in charmonium case and the parameter a has been obtained from Eq.(32)using M=6.277 for 1S state.Similarly forparameters a and b are determined after fixing d suitably.The value of parameter c,in all cases,was calculated by using Eq.(30).The complete mass spectra of heavy and light mesons are tabulated in Tables 1–6.The variations of interaction potential with inter-quark separation r for various mesons are shown in Figs.1–3.

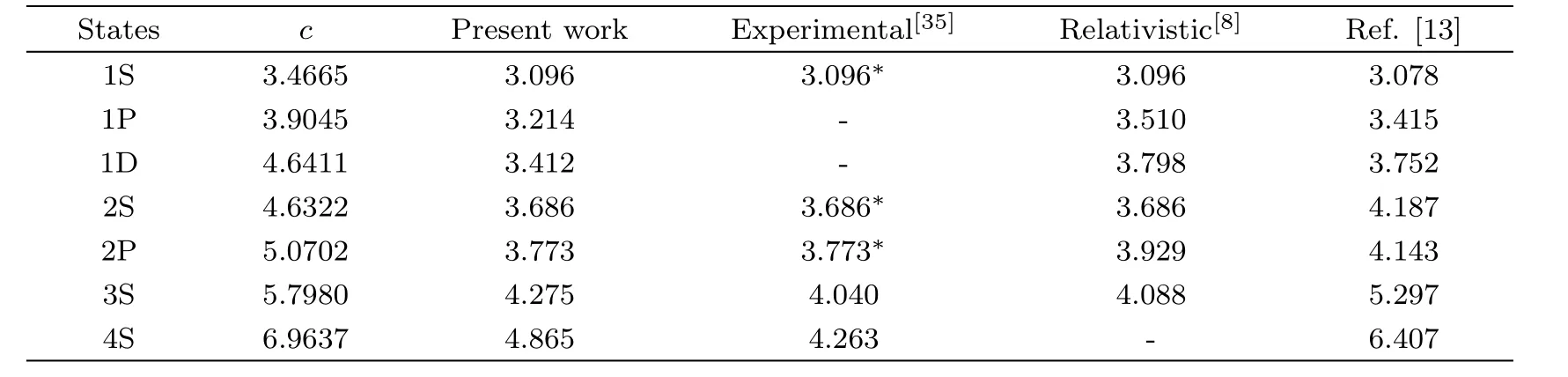
Table 1 Mass spectra of charmonium(a=0.0297 GeV3,b=0.2209 GeV2,d=4.8542 GeV−1)in GeV/C2.

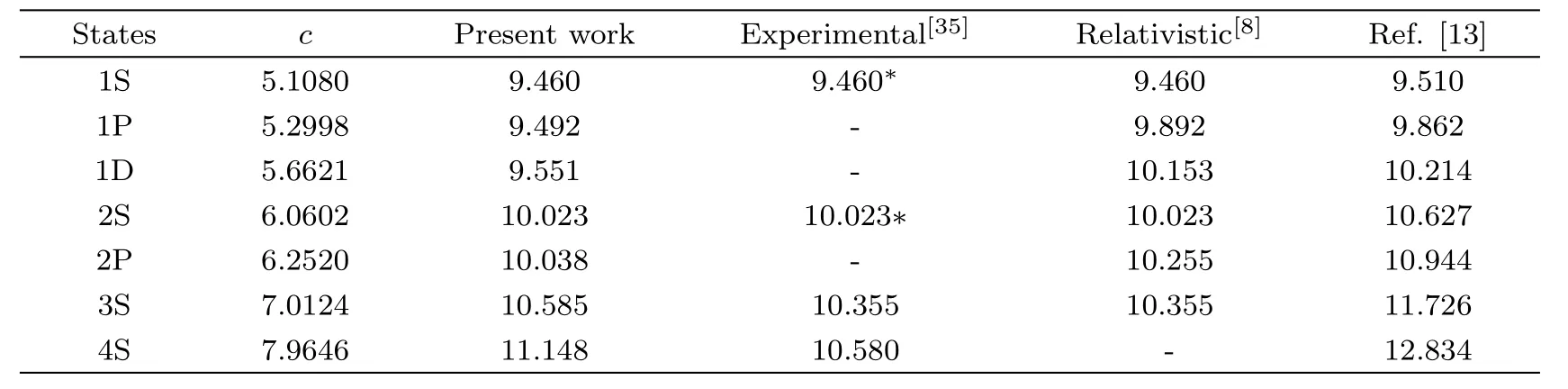
Table 2 Mass spectra of bottomonium(a=0.0289 GeV3,b=0.3555 GeV2,d=4.8542 GeV−1)in GeV/C2.

Table 3 Mass spectra of(a=0.0204 GeV3,b=0.2209 GeV2,d=4.8542 GeV−1)in GeV/C2.

Table 3 Mass spectra of(a=0.0204 GeV3,b=0.2209 GeV2,d=4.8542 GeV−1)in GeV/C2.

States c Present work Experimental[35] Relativistic[8] Ref.[13]1S 4.0087 6.277 6.277∗ 6.332 6.277 1P 4.3500 6.340 - 6.734 6.666 1D 4.9539 6.452 - 7.072 -2S 5.1208 6.814 - 6.881 7.042 2P 5.4621 6.851 - 7.126 7.207 3S 6.2329 7.351 - 7.235 7.384 4S 7.3450 7.889 - - -

Table 4Mass spectra of(a=0.0122 GeV3,b=0.0688 GeV2,d=4.8542 GeV−1)in GeV/C2.

Table 4Mass spectra of(a=0.0122 GeV3,b=0.0688 GeV2,d=4.8542 GeV−1)in GeV/C2.

States c Present work Experimental[31] Relativistic[34] Ref.[11]1S 18.2251 2.512 - 2.129 1.968 1P 22.0717 2.649 - 2.549 2.566 1D 27.9841 2.859 2.859∗ 2.899 2.857 2S 26.1194 2.709 2.709∗ 2.732 2.709 2P 29.9659 2.860 - 3.018 -3S 34.0136 2.906 - 3.193 2.932 4S 41.9079 3.102 - 3.575 -

Table 5Mass spectra of(a=0.0372 GeV3,b=0.2796 GeV2,d=0.1232 GeV−1)in GeV/C2.

Table 5Mass spectra of(a=0.0372 GeV3,b=0.2796 GeV2,d=0.1232 GeV−1)in GeV/C2.

States c Present work Experimental[35−36] Relativistic[32]1S 1.7943 5.415 5.415∗ 5.450 1P 3.3520 5.830 5.830∗ 5.857 1D 4.9816 6.264 - 6.182 2S 3.4444 6.819 - 6.012 2P 5.0021 6.786 - 6.279 3S 5.0946 8.225 - 6.429 4S 6.7447 9.629 - 6.773

Table 6Mass spectra of(a=0.0178 GeV3,b=0.1589 GeV2,d=0.1232 GeV−1)in GeV/C2.

Table 6Mass spectra of(a=0.0178 GeV3,b=0.1589 GeV2,d=0.1232 GeV−1)in GeV/C2.

States c Present work Experimental[35−36] Relativistic[32]1S 1.9283 5.325 5.325∗ 5.371 1P 3.7065 5.723 5.723∗ 5.777 1D 5.5315 6.131 - 6.110 2S 3.7657 6.413 - 5.933 2P 5.5440 6.486 - 6.197 3S 5.6032 7.501 - 6.355 4S 7.4407 8.589 - 6.703

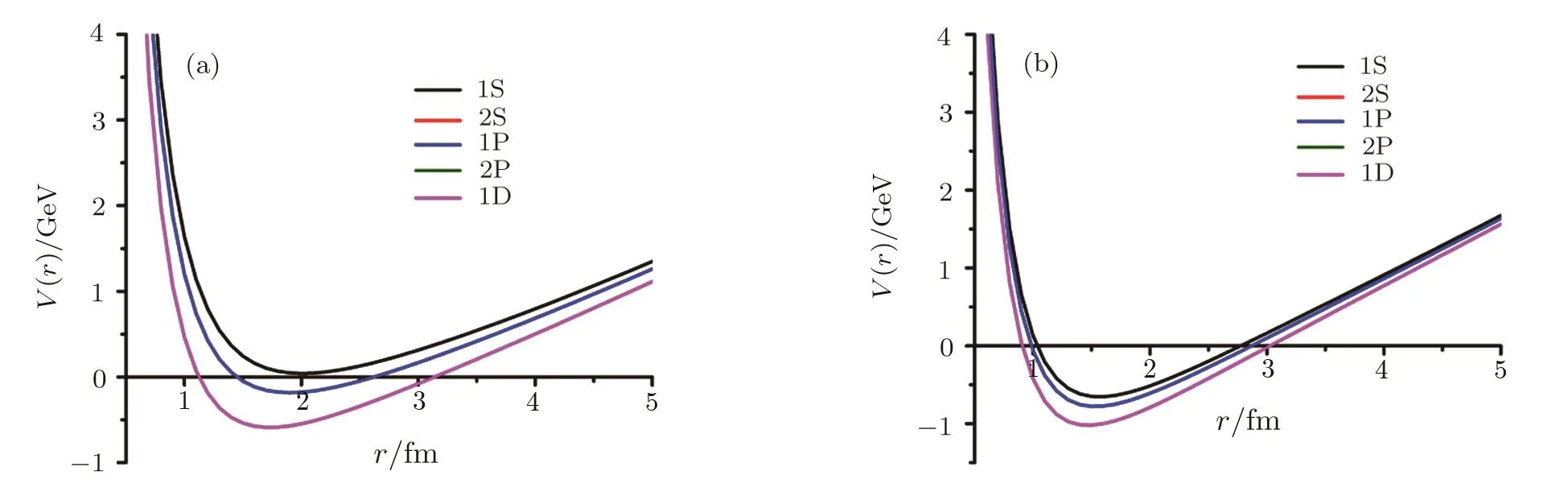
Fig.1 Variation of interaction potential(1)with inter quark separation for(a)charmonium and(b)bottomonium.

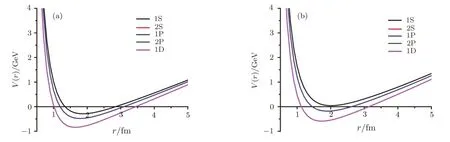
Fig.2 Variation of interaction potential(1)with inter quark separation for(a) and(b)

Fig.3 Variation of interaction potential(1)with inter quark separation for(a)

4 Conclusions

In the present work,the AIM has successfully been employed to determine the analytical solutions to the non-relativistic radial SE in three-dimensional space.Using this technique,the energy eigenvalues expression(cf Eq.(29))is derived for the interaction potential(1),which represents here the interaction between quark and antiquark in a meson system.The potential(1)is an extended form of Cornell potential,which includes harmonic and anharmonic terms and also finds applications in quantum dot systems.[15−16]From the energy eigenvalues expression,mass spectra ofmesons are obtained(see Tables 1–6).The obtained results of present study,particularly for lower states,are in good agreement with experimental data[31,35−36]and other theoretical results,calculated via relativistic quark models[8,34]and are improved in comparison with other studies.[12−13,18]We hope,this work may be useful to calculate mass spectra of other mesons,radiative transition widths and their strong decay widths.Furthermore,the ubiquitous interaction potential(1)has interesting bearings to generate bound energy states of many diatomic molecules and quantum dot systems.

Acknowledgments

One of the authors,RR acknowledges the University Grant Commission(UGC),New Delhi(India)for granting financial support through the UGC-BSR fellowship.