An Approximate Approach for Systems of Singular Volterra Integral Equations Based on Taylor Expansion

Mohsen Didgarand Alireza Vahidi

1Department of Mathematics,Guilan Science and Research Branch,Islamic Azad University,Rasht,Iran

2Department of Mathematics,Rasht Branch,Islamic Azad University,Rasht,Iran

3Department of Mathematics,College of Science,Yadegar-e-Emam Khomeyni(RAH)Shahr-e-Rey Branch,Islamic Azad University,Tehran,Iran

AbstractIn this article,an extended Taylor expansion method is proposed to estimate the solution of linear singular Volterra integral equations systems.The method is based on combining the m-th order Taylor polynomial of unknown functions at an arbitrary point and integration method,such that the given system of singular integral equations is converted into a system of linear equations with respect to unknown functions and their derivatives.The required solutions are obtained by solving the resulting linear system.The proposed method gives a very satisfactory solution,which can be performed by any symbolic mathematical packages such as Maple,Mathematica,etc.Our proposed approach provides a significant advantage that the m-th order approximate solutions are equal to exact solutions if the exact solutions are polynomial functions of degree less than or equal to m.We present an error analysis for the proposed method to emphasize its reliability.Six numerical examples are provided to show the accuracy and the efficiency of the suggested scheme for which the exact solutions are known in advance.

Key words:systems of singular Volterra integral equations(SSVIEs),systems of generalized Abel’s integral equations,error analysis,Taylor expansion

1 Introduction

Singular integral equations appear frequently in mathematical physics and have various applications in different fields including fluid mechanics,solid mechanics,quantum mechanics,bio-mechanics,astronomy,optics,electromagnetic theory,X-ray radiography,seismology,optical if ber evaluation,atomic scattering,radar ranging,electron emission,plasma diagnostics,and microscopy.[1]In recent years,approximate solution of integral equations has attracted great attention of many researchers[1−8]while numerical solution of weakly singular integral equations has been less considered.[9−18]Abel’s integral equation is one of the famous and important singular integral equations that arises from physical or mechanical models without passing through a differential equation.The general form of Abel’s integral equation is

As mechanical description of Abel’s integral equation consider a point of mass moving in the gravity field on a smooth curve lying in a vertical plane.Let f(x)show the time in which the point mass reaches the lowest point while released from the height x.The problem is to find the equation of the curve.Abel’s integral equation is formulation of this problem.[1]

Study and investigation of approximate solutions for systems of singular integral equations play a significant role in applied sciences,since they are not generally easy to solve analytically.Thus a variety of numerical and approximate methods have been developed to solve these,such as operational matrices,[19]homotopy perturbation method(HPM),[20]homotopy analysis method(HAM),[21]fractional differential transform method,[22]extrapolation method,[23]Legendre wavelets,[24]and Sinc approximation with the single exponential(SE).[25]

Li[26]proposed a novel application of Taylor expansion method for approximate solution of linear ordinary differential equations with variable coefficients.The method expanded by Li and his co-authors to solve Abel’s integral equation,[18,27]Riccati equation,[28]an integral equation with fixed singularity for a cruciform crack,[29]a class of linear integro-differential equations,[30]and fractional integro-differential equations.[31]Vahidi and Didgar improved the Taylor expansion method proposed in Ref.[28]for determining the solution of Riccati equations.[32]Didgar and Ahmadi expanded the method proposed in Ref.[26]for solving systems of linear ordinary and fractional differential equations.[33]Moreover,Maleknejad and Damercheli[34]developed the method for solving linear second kind Volterra integral equations system.This investigation is an effort to propose a novel application of Taylor expansion[18,26−34]for solving systems of singular integral equations which possesses high accuracy.By expanding unknown functions as an m-th order Taylor poly-nomial and employing integration method,system of singular integral equations is converted into a new system of linear equations with respect to unknown functions and their derivatives.Then,intended approximate solutions can be obtained by solving the resulting linear system using a standard method.Besides simplicity and applicability,the considerable advantage of this method is that an m-th order approximation tends to the exact solution if it be a polynomial function of degree at most m.

The paper is arranged as follows.In Sec.2,a method for systems of singular integral equations is described.An error analysis is given in Sec.3.In Sec.4,the accuracy and efficiency of the method is illustrated by considering six numerical examples.Section 5 is devoted to conclusions.

2 Description of the Method

Consider the following system of singular Volterra integral equations

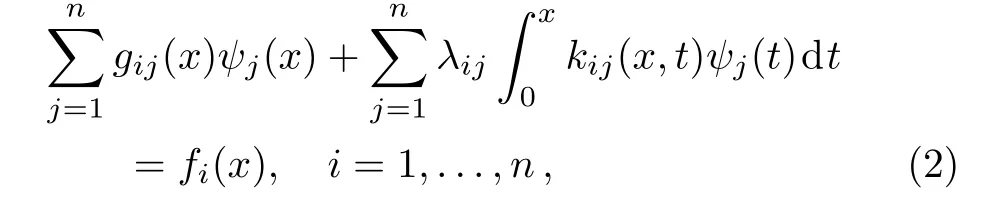
where λij(i,j= 1,...,n)are real constants,gij(x)(i,j=1,...,n)and fi(x)(i=1,...,n)are given functions in C(I)where I is the interval of interest.The ψj(x)(j=1,...,n)are unknown functions to be determined and kijare singular kernels of the form

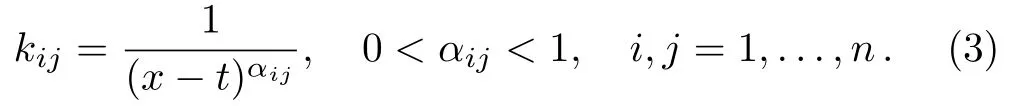
In this section we aim to show how the Taylor expansion method can be applied to the approximate solutions of singular system(2).Toward this end,we convert the SSVIEs into a system of linear equations with respect to unknown functions and their derivatives.This needs the desired solutions ψj(t)to be m+1 times continuously differentiable on the interval I,in other words ψj∈ Cm+1(I).Therefore,for ψj∈ Cm+1(I),the unknown functions ψj(t)can be expressed in terms of the m-th order Taylor series at an arbitrary point x∈I as

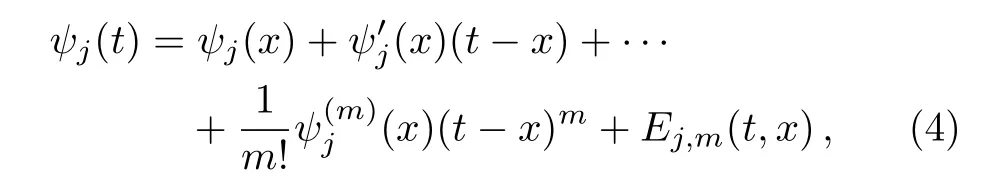
where Ej,m(t,x)indicates the Lagrange error bound

for some point ξjbetween x and t.Generally,the Lagrange error bound Ej,m(t,x)becomes sufficiently small as m gets great enough.Especially,if the solutions ψj(t)are polynomial functions of degree up to m,then the Lagrange error bound becomes zero,namely,the obtained approximate solutions of system(2)yield the exact solutions.Based on the aforementioned assumption,by omitting the last Lagrange error bound,we consider the truncated Taylor expansion ψj(t)as

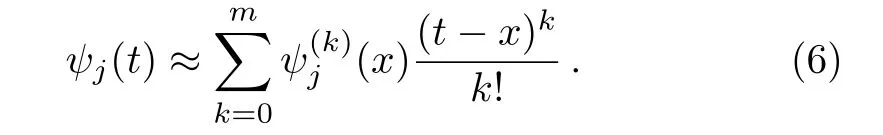
Inserting the approximate relation(6),for unknown function ψj(t),into Eq.(2)and in view of Eq.(3),we obtain

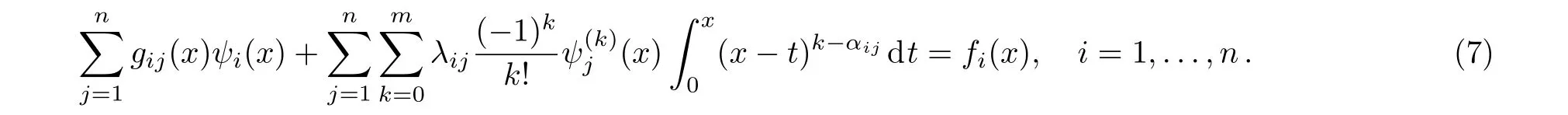
In fact,Eq.(2)was converted into a linear system of ordinary differential equations with respect to ψj(x)and its derivatives up to order m.In other word,we have obtained n linear equations in Eq.(7)with respect to n×(m+1)unknown functionsfor k=0,...,m,j=1,...,n.In the following,we want to determineby solving a system of linear equations.In order to achieve this goal,other n×m independent linear equations with respect toare needed,which can be obtained by integrating both sides of Eq.(2)m times with respect to x from 0 to s and with the help of changing the order of the integrations.Thus,we have

where

in which the variable s has replaced by x,for simplicity.Similarly,we apply the Taylor expansion again and substituting(6)for ψj(t)into Eq.(8)results in

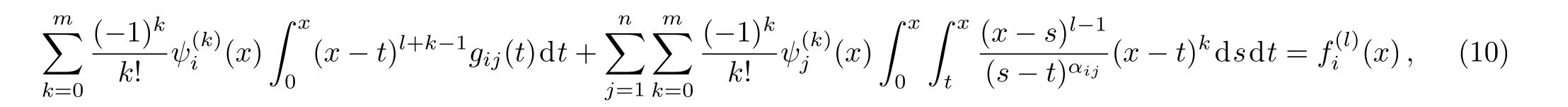
for l=1,...,m.

In this way,Eqs.(7)and(10)construct a system of linear equations with respect to the unknown functions ψj(x)and its derivatives up to order m.In the following,we indicate this system as

where

and in coefficient matrix(12),the first n rows refer to coefficients ofin Eq.(7)for k=0,...,m,j=1,...,n and the other rows refer to coefficients ofinfor k=1,...,m are determined by solving the resulting linear system but in point of fact,it is ψj(x)that we need.

3 Error Analysis

This section belongs to the stability analysis of the scheme and the error analysis proposed in Ref.[18]will be expanded for derived m-th order approximate solution of singular integral equations system(2)in order to get theoretical features about the convergence of the suggested method.We assume that the exact solutions ψj(t)are infinitely differentiable on the interval I;so ψj(t)can be expanded as an uniformly convergent Taylor series in I as follows Eq.(10)for l=1,...,m.Ultimately,the resulting system(11)can be solved by any appropriate method to obtain unknown functions.We note that not only ψj(x)but also

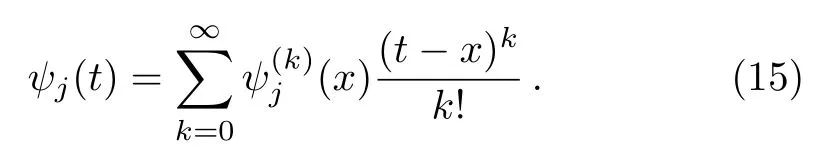
Using the proposed method given in Sec.2,SSVIEs can be converted into an equivalent system of linear equations with respect to unknown functionsk=0,1,...as

where

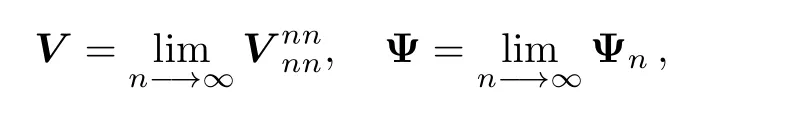
Hence,under the solvability conditions of system(16)and letting B=V−1,the unique solution of system(16)is represented as

We rewrite relation(19)in an alternative matrix form as

Accordingly,we can find out that the vector Ψnconsists of the first n(m+1)elements of the exact solution vector Ψ must satisfy the following relation

According to the proposed process,the unique solution of SSVIEs(2)can be denoted as

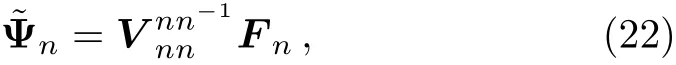
where Ψnis replaced bynas its approximate solution.

Subtracting Eq.(22)from Eq.(21)leads to

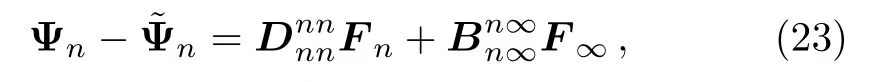
Now,we expand the right-hand side of Eq.(23),the first n elements of the vector at the left-hand side of Eq.(23)can be expressed as

where

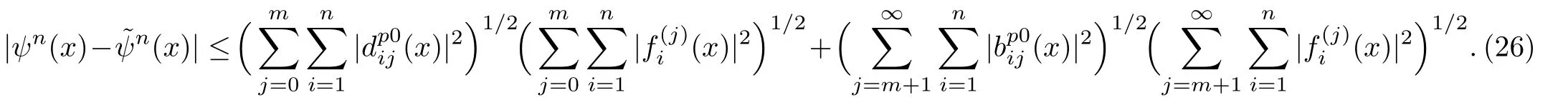
4 Numerical Examples

In this section,six numerical examples are considered in order to establish the applicability and the accuracy of the proposed method.The results are compared with previous reports results to illustrate that the suggested method is not only accurate but also quite stable.In the following examples,absolute errors of the m-th order approximate values ψi,m(x)and the corresponding exact values ψi(x)asare determined.All computations were performed using Mathematica 8.

Example 1Consider the following system of singular Volterra integral equations[19]

with the exact solutions ψ1(x)=x and ψ2(x)=1.

Using the proposed method in Sec.2,we obtain the approximate solutions of the problem(27)and it is important to note that after converting system(27)into a system of linear equations the Mathematica command“LinearSolve” is used for the new system.We can find by setting m=1,the first-order approximate solution yields the exact solution as expected,since the m-th order approximate solution yields the exact solution if the exact solution is a polynomial function of degree up to m.

This example has been solved by operational matrices of piecewise constant orthogonal functions[19]on the interval[0,1).We present the maximum of the absolute errors obtained from Ref.[19]in Table 1.

Table 1 The maximum of the absolute errors in Ref.[19].

Table 2 Absolute errors of Example 2 for ψ1(x).

Example 2Consider the following integral equations system[22,25]

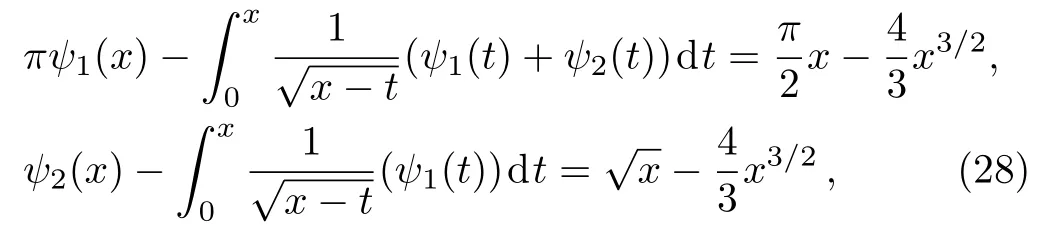
Example 3The following system of integral equations

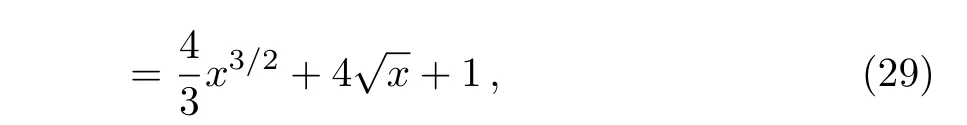
is considered in Ref.[25]with the exact solutions ψ1(x)=x and ψ2(x)=1.Employing the process described in Sec.2,by setting m=1,the first-order approximate solution of Eq.(29)results in the exact solution,as expected.This example was used in Ref.[25]and has been solved by SE-Sinc method.Tables 6 and 7 are related to the numerical results obtained from Ref.[25].

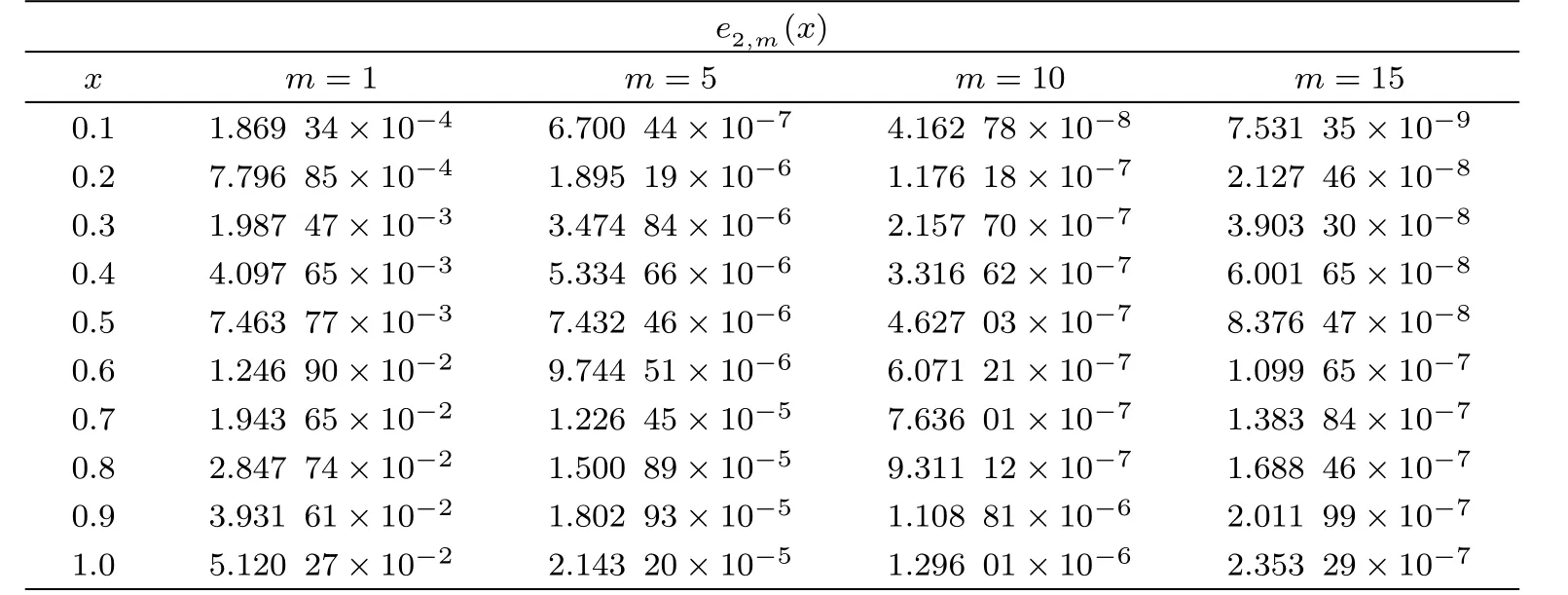
Table 3 Absolute errors of Example 2 for ψ2(x).

Table 4 Absolute errors of Example 2 by SE-Sinc method in Ref.[25]for ψ1(x).

Table 6 Absolute errors of Example 3 by SE-Sinc method in Ref.[25]for ψ1(x).

Example 4Consider the following system of Abel’s integral equations of the second kind[21]

Table 7 Absolute errors of Example 3 by SE-Sinc method in Ref.[25]for ψ2(x).

From Tables 8 and 9,we can find that the accuracy of our results is quite satisfactory and more accurate results can be obtained by taking higher-order m.This example was used in Ref.[21]and has been solved by homotopy analysis method.Figures 1 and 2 are related to the absolute errors of ψ1(x)and ψ2(x),respectively,in Ref.[21].From Tables 8 and 9 and Figs.1 and 2,we observe that the results obtained by Taylor expansion method are much better than those obtained in Ref.[21].

Example 5Consider the following system of Abel’s integral equations of the second kind[21]with the exact solutions ψ(x)=x and

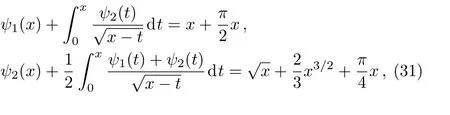
1We obtain the approximate solutions by setting m=1,5,10,15.In the following,absolute errors are shown in Tables 10 and 11.From Tables 10 and 11,we observe that the accuracy of our results is quite satisfactory and more accurate results can be obtained by taking higherorder m.This example was used in Ref.[21]and has been solved by homotopy analysis method.Figures 3 and 4 are related to the absolute errors of ψ1(x)and ψ2(x),respectively,in Ref.[21].From Tables 10 and 11 and Figs.3 and 4,we can find that the results obtained by Taylor expansion method are much better than those obtained in Ref.[21].

Table 8 Absolute errors of Example 4 for ψ1(x).

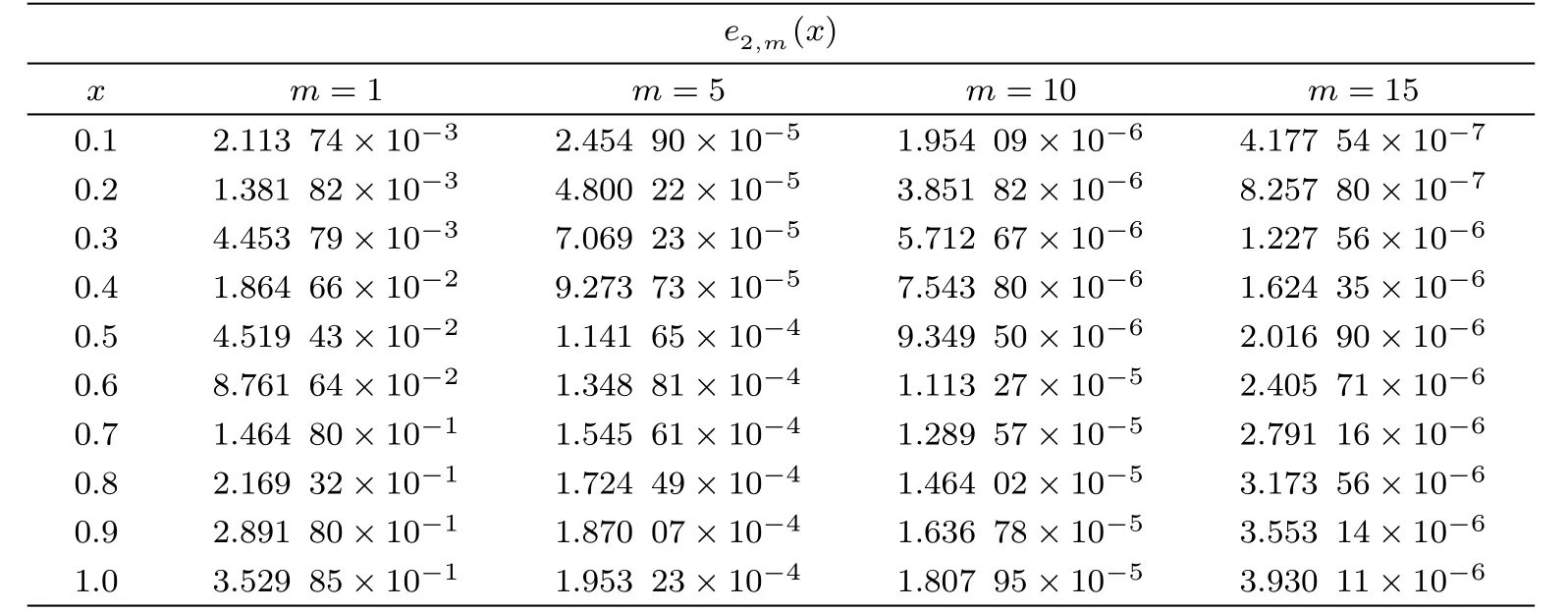
Table 9 Absolute errors of Example 4 for ψ2(x).

Table 10 Absolute errors of Example 5 for ψ1(x).

Example 6Consider the following singular integral equations system of the first kind[1]

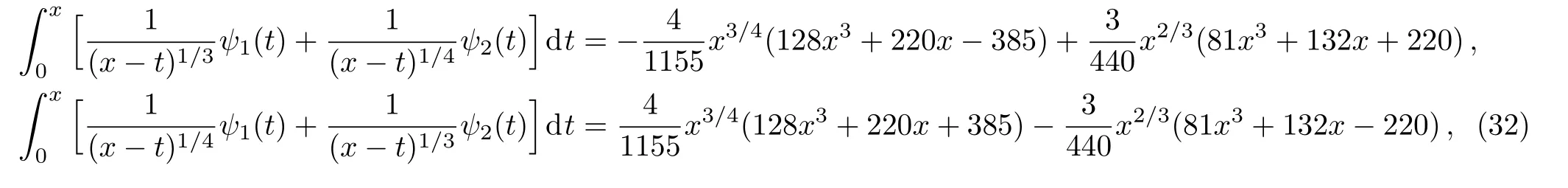
with the exact solutions ψ1(x)=1+x+x3and ψ2(x)=1−x−x3.We evaluate the approximate solutions by setting m=1,2,3 and the obtained absolute errors are shown in Tables 12 and 13.We observe that the accuracy of our results is quite satisfactory and the third-order approximate solution yields the exact value,as expected.

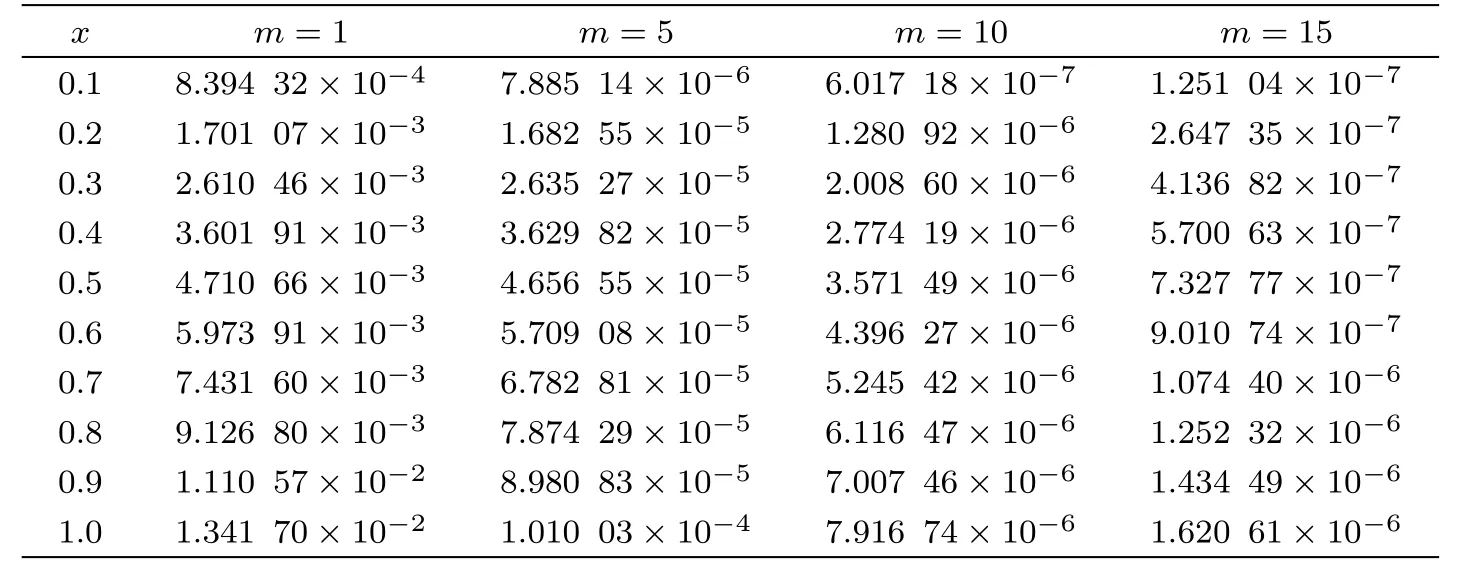
Table 11 Absolute errors of Example 5 for ψ2(x).

Table 12 Absolute errors of Example 6 for ψ1(x).

5 Conclusion

The main objective of this investigation was to present a new application of Taylor expansion to conveniently solve linear singular integral equations systems.By employing the Taylor expansion of unknown functions at an arbitrary point and integration method,the SSVIEs has been converted into a system of linear equations with respect to unknown functions and their derivatives.The stability analysis of the method was also carried out and we have demonstrated the practicality and efficiency of our proposed method by several numerical examples.In particular for such cases when the exact solutions are polynomial functions of degree at most m,the derived m-th order approximations are equal to exact solutions.

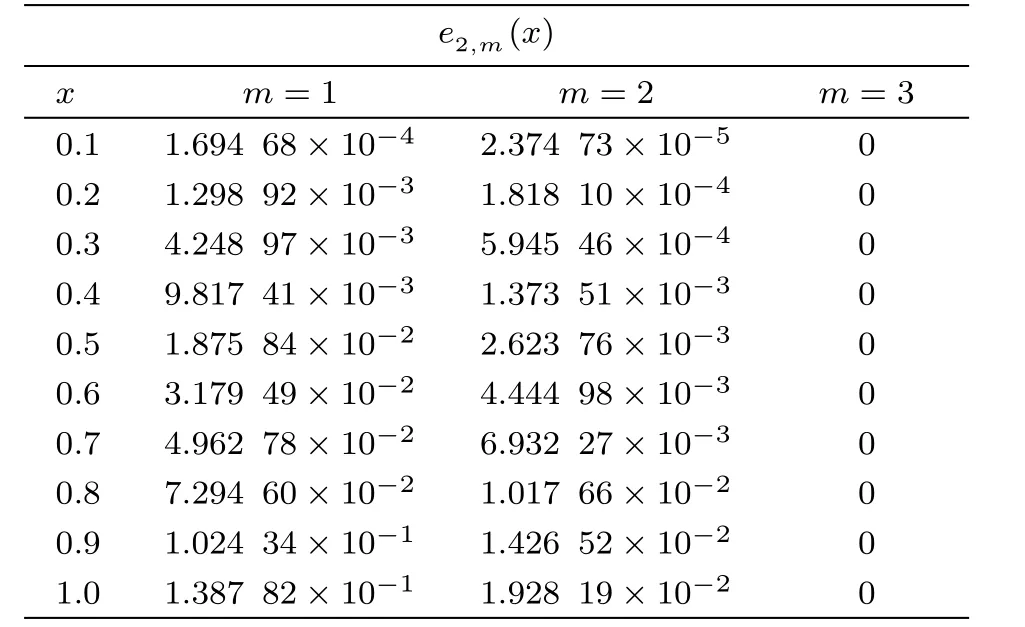
Table 13 Absolute errors of Example 6 for ψ2(x).

Fig.1 The absolute error of ψ1(x)in Ref.[21].

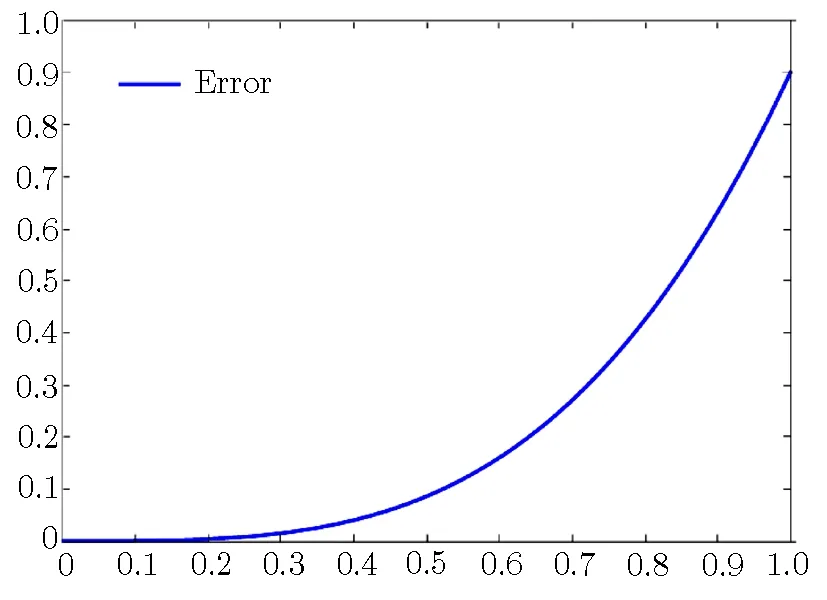
Fig.2 The absolute error of ψ2(x)in Ref.[21].

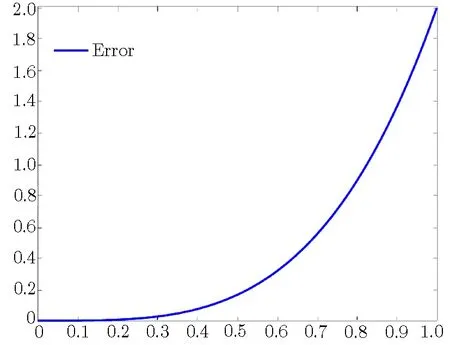
Fig.3 The absolute error of ψ1(x)in Ref.[21].

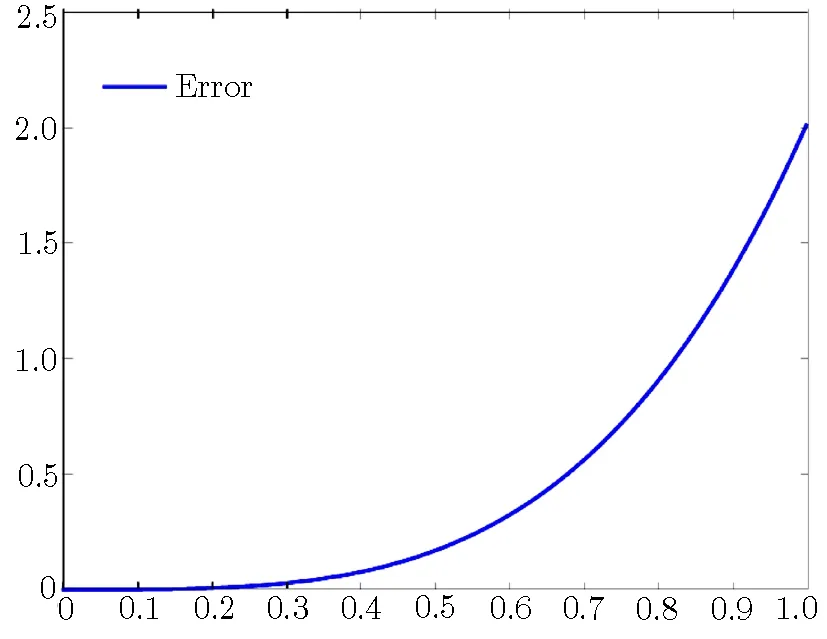
Fig.4 The absolute error of ψ2(x)in Ref.[21].