Sufficient Conditions of the Same State Order Induced by Coherence∗

Fu-Gang Zhang(张福刚)and Yong-Ming Li(李永明),2,†

1School of Mathematics and Information Science,Shaanxi Normal University,Xi’an 710119,China

2College of Computer Science,Shaanxi Normal University,Xi’an 710119 China

AbstractIn this paper,we study coherence-induced state ordering with Tsallis relative entropy of coherence,relative entropy of coherence and l1norm of coherence,and give the sufficient conditions of the same state order induced by above coherence measures.First,we show that the above measures give the same ordering for single-qubit states in some special cases.Second,we consider some special states in a d-dimensional quantum system.We show that the above measures generate the same ordering for these special states.Finally,we discuss dynamics of coherence-induced state ordering under Markovian channels.We find amplitude damping channel changes the coherence-induced ordering even though for single-qubit states with fixed mixedness.

Key words:Tsallis relative entropy of coherence,relative entropy of coherence,l1norm of coherence,coherence-induced state ordering

1 Introduction

Quantum coherence is one of the most important physical resources in quantum mechanics,which can be used in quantum optics.[1]quantum information and quantum computation,[2]thermodynamics,[3−4]and low temperature thermodynamics.[5−7]Many efforts have been made in quantifying the coherence of quantum states.[8]The authors of Ref.[9]have proposed a rigorous framework to quantify coherence.The framework gives four conditions that any proper measure of the coherence must satisfy.Based on this framework,one can de fine suitable measures with respect to the prescribed orthonormal basis.The relative entropy of coherence and the l1norm of coherence[10]have been proved to satisfy all four conditions.Recently,the author of Ref.[10]has proposed Tsallis relative entropy of coherence.The author has proved Tsallis relative entropy of coherence satisfies all conditions but monotonicity under incoherent selective measurements.Whereas,this coherence measure satisfies a generalized monotonicity for average coherence under subselection based on measurement.[10]In addition,various other coherence measures have also been discussed.[10−18]Many further discussions about quantum coherence have been aroused.[19−36]

Up to now,many different coherence measures have been proposed based on different physical contexts.For the same state,different values of coherence will be obtained by different coherence measures.In this case,a very important question arises,whether these measures generate the same ordering. We say that two coherence measures Cmand Cngenerate the same ordering if they satisfy the condition Cm(ρ) ≤ Cm(σ)if and only if Cn(ρ) ≤ Cn(σ)for any density operators ρ and σ.We say a state ρ is a pure state if tr(ρ2)=tr(ρ)=1.If ρ is not pure,then we say it is a mixed state.References[19]and[20]have showed that the Tsallis relative entropy of coherence,relative entropy of coherence and the l1norm of coherence only generate the same ordering for singlequbit pure states.They do not give the same ordering for single-qubit mixed states or high dimension states even though high dimension pure states.

Based on these discussions,some further questions will be put forward as follows.(i)In addition to singlequbit pure states,whether or not there exist other sets of states such that above coherence measures generate the same ordering.(ii)Given a quantum incoherent operator,whether or not coherence-induced state ordering will be changed.

In the paper,we will try to resolve these two questions.Our discussion focuses on the Tsallis relative entropy of coherence,relative entropy of coherence and the l1norm of coherence.For question(i),we show that these three measures generate the same ordering for some particular sets of states,such as for some single-qubit states with a fixed mixedness or a fixed nz.For question(ii),we discuss dynamics of coherence-induced state ordering under Markovian channels,we show that amplitude damping channel changes the coherence-induced ordering even though for single-qubit states with fixed mixedness,but amplitude damping channel does not change the coherence-induced ordering for some single-qubit states with fixed valued nz.Other Markovian channels can be discussed by a similar method.

This paper is organized as follows.In Sec.2,we briefly review some notions related to Tsallis relative entropy of coherence,relative entropy of coherence and l1norm of coherence.In Sec.3,we show that Tsallis relative entropy of coherence,relative entropy of coherence and l1norm of coherence generate the same ordering for single-qubit states with a fixed mixedness or a fixed length along the direction σz.In Sec.4,we show that they generate the same ordering for some particular sets of high dimensional states.In Sec.5,we discuss dynamics of coherence-induced ordering under Markovian channels.We summarize our results in Sec.6.

2 Preliminaries

In this section,we review some notions related to quantifying quantum coherence. Considering a finite dimensional Hilbert space H with d=dim(H).Let{|i⟩,i=1,2,...,d}be a particular basis of H.A state is called an incoherent state if and only if its density operator is diagonal in this basis,and the set of all the incoherent states is usually denoted as∆.Baumgratz et al.[9]proposed that quantum coherence can be measured by a function C that maps a state ρ to a nonnegative real value,moreover,C must satisfy following properties:(C1)C(ρ) ≥ 0 and C(ρ)=0 if and only if ρ ∈ ∆;(C2a)C(ρ) ≥ C(Φ(ρ)),where Φ is any incoherent completely positive and trace preserving maps;wherefor all Kiwithandfor any ensemble

In accordance with the criterion,several coherence measures have been studied.It has been shown that l1norm of coherence and relative entropy of coherence satisfy these four conditions.[9]l1norm of coherence[9]is defined as

here ρijare entries of ρ.The coherence measure de fined by the l1norm is based on the minimal distance of ρ to the set of incoherent states ∆,with D being the l1norm,and 0≤ Cl1(ρ)≤ d−1.

The relative entropy of coherence[9]is de fined as

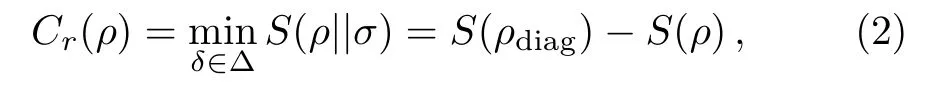
where S(ρ||σ)=tr(ρlogρ − ρlogσ)is the quantum relative entropy,S(ρ)=tr(ρlogρ)is the von Neumann entropy,and∑in this paper,log has base 2.The coherence measure de fined by the relative entropy is based on the minimal distance of ρ to ∆,with D being the relative entropy,and 0 ≤ Cr(ρ)≤ logd.

For any α ∈ (0,1)⊔(1,2],Tsallis relative entropy of coherence,[10]denoted by Cα(ρ),is de fined as

The author of Ref.[10]proved that Cαsatisfies the conditions of(C1),(C2a)and(C3)for all α∈(0,2],but it violates(C2b)in some situations.However,Cαsatisfies a generalized monotonicity for the average coherence under subselection based on measurement as the following form.[10]Tsallis relative entropy of coherence Cα(ρ)satisfies

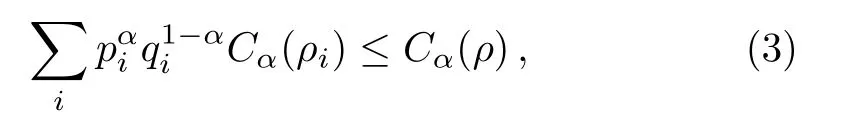
Rastegin gave an elegant mathematical analytical expression of Tsallis relative entropy of coherence.[10]Given α ∈ (0,1)∪(1,2],and a state ρ,the Tsallis relative entropy of coherence Cα(ρ)can be expressed as

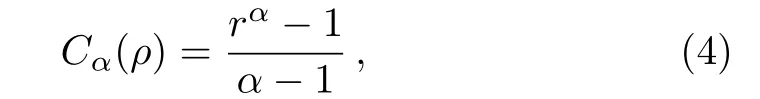
where

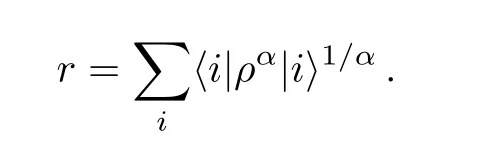
For the given ρ and α,based on this coherence measure,the nearest incoherence state from ρ is the state

Considering an interesting case α=2,

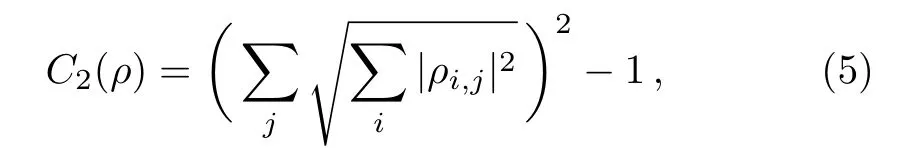
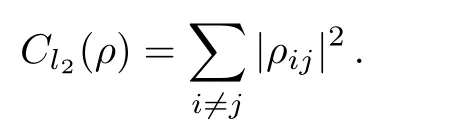
It has been shown that Cl2does not satisfy the condition(C2b).[9]Although C2also violates the condition(C2b),it obeys a generalized monotonicity property Eq.(3).[10]

For any state ρ,the mixedness based on normalized linear entropy[40]is given as

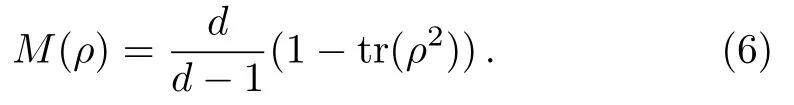
In particular,when ρ is a single-qubit state,M(ρ)=2(1−tr(ρ2)).

3 Single-Qubit States

In this section,we consider a 2-dimensional quantum system.A general single-qubit state can be written as

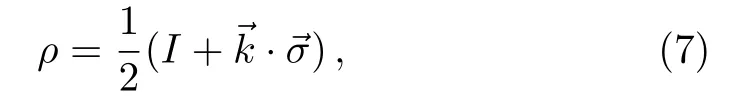
Substituting Eq.(8)into Eq.(6),we obtain the mixedness of single-qubit state ρ as follow

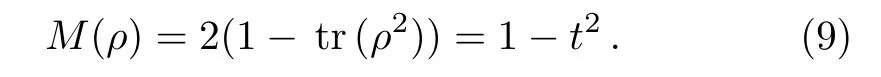
According to the expression of mixedness,we find that the mixedness is only related to the length t.In the case of t=1,the state becomes a pure state.In Refs.[19]and[20],authors foundand Cαgive the same ordering states for all single-qubit pure states.Here,we generalize this result.We will show that these coherence measures also give the same ordering for all states with a fixed mixedness.

By a routine calculation,we obtain the eigenvalues of ρ,

Their norm eigenvectors are

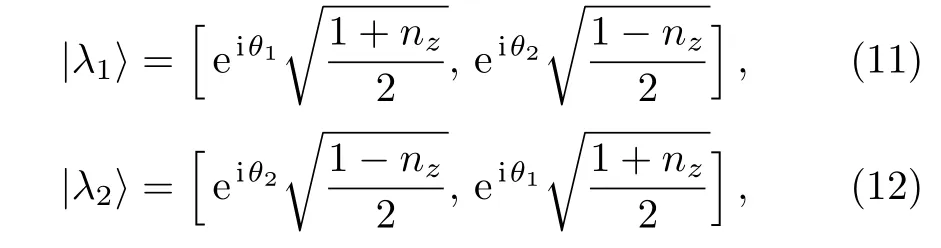
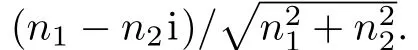
Relative entropy of coherence

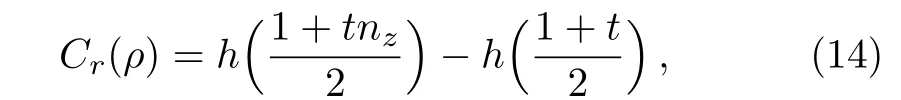
where h(x)= −xlog(x)−(1−x)log(1−x).Tsallis relative entropy of coherence

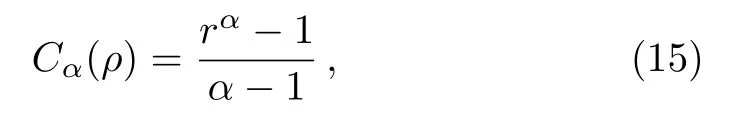
where

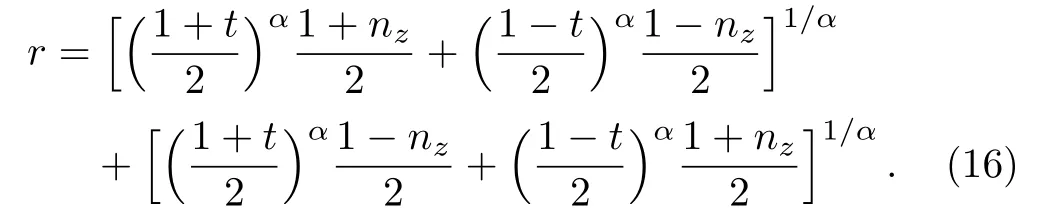
According to Eq.(9),we know that all states with the same mixedness have the same length t.It is easy to find,for a fixed value t,Eqs.(13),(14),(15)are symmetric functions with respect to nz=0,in other words,these three coherence measurements depend on|nz|and t.Hence,here we only consider the case of nz∈[0,1].We give the following proposition.

Propsition 1Given a fixed value t,and α ∈ [0,1)∪(1,2],Eqs.(13),(14),(15)are decreasing functions with respect to nz.

ProofIt is obvious that Eq.(13)is a decreasing function with respect to nzfor nz∈[0,1].Since

we have that Cr(ρ)is a decreasing function with respect to nzfor nz∈[0,1].

Let

we consider the derivation of the expression of Eq.(16),

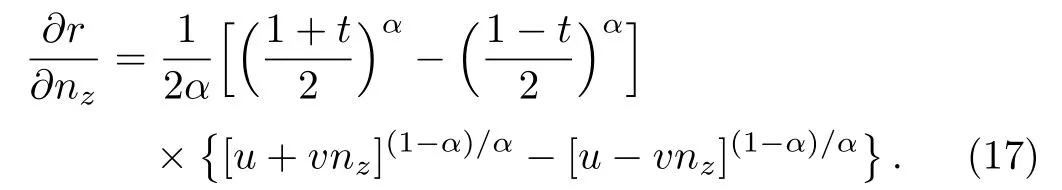
Due to t∈[0,1],we have u≥v≥0,then u+vnz≥u−vnzfor nz∈ [0,1],hence we have∂r/∂nz≤ 0 in the case of α ∈ (1,2],and ∂r/∂nz≥ 0 in the case of α ∈ [0,1).Substituting these results into Eq.(15),we have that Eq.(15)is a decreasing function with respect to nz. ?

In the following,we discuss the ordering states for all single qubit states with a fixed mixedness.

Theorem 1For any α ∈ [0,1)∪(1,2],the coherence measures Cl1,Cr,and Cαhave the same ordering for all single-qubit states with a fixed mixedness M.

ProofLet ρ, σ be two single-qubit states with a fixed mixedness M.It is obvious that ρ,σ have the same value t by means of Eq.(9).According to Proposition 1,we have?

Theorem 1 has shown that Cl1,Crand Cαhave the same ordering for all single qubit states with a fixed mixedness.It is quite natural that we will ask whether these coherence measures have the same ordering for all states with a fixed value nz.For all single qubit states with a fixed value nz,since it is very difficult to discuss the monotonicity of the expressions of Cαwith respect to t for any α∈[0,1)∪(1,2],then we only discuss the special situations of α=2,1/2 by analytical method.In fact,we find the result is also valid for other values α ∈ (0,1)∪(1,2]by numerical method.In Fig.1,we discuss the monotonicity of Cαwith respect to t when α =1/4,3/4,3/2 for fixed nz=1/4,1/2,3/4.We find the following result is valid in these situations.For the other situations,we can discuss them by a similar method.

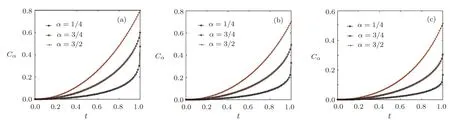
Fig.1 Three special Tsallis relative entropy of coherence C1/4,C3/4and C3/2are increasing functions with respect t for the fixed(a)nz=1/4,(b)nz=1/2,(c)nz=3/4.

Proposition 2Given a fixed value nz,Eqs.(13),(14),(15)are increasing functions with respect to t,where α=1/2,2.

ProofIt is obvious that Cl1(ρ)is an increasing function with respect to t.Since

then

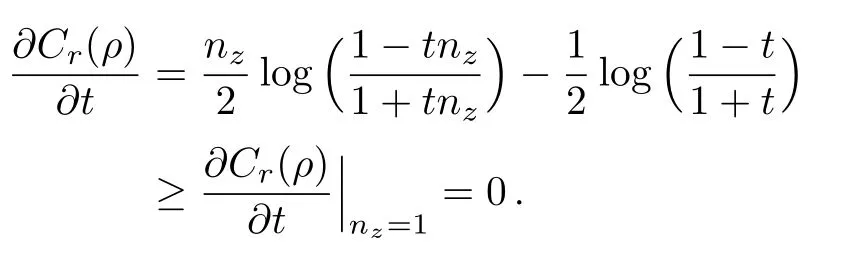
Therefore,Cr(ρ)is an increasing function with respect to t.

In order to discuss the monotonicity of C2and C1/2with respect to t,we first consider the monotonicity of r(Eq.(16))with respect to t when α=1/2,2.For convenience,let m=(1+t)/2,n=(1+nz)/2,it is obvious that 1/2≤m,n≤1.Substituting m,n into Eq.(16),and by a routine calculation,we have

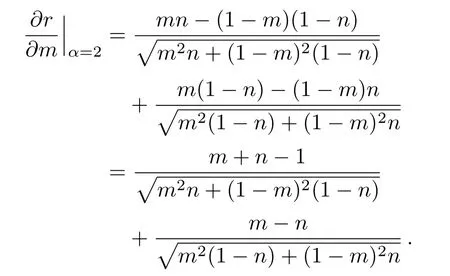
If m ≥ n,it is easy to findIf m ≤ n,we consider

When α=1/2,by a routine calculation,we have

Substituting above results into Eq.(15),we have

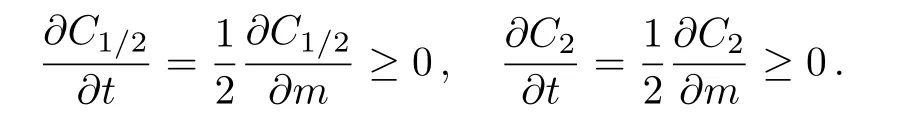
Therefore,Eqs.(14)and(15)are increasing functions with respect to t for single qubit states with a fixed value nz.?

On the basis of the above proposition,we discuss the ordering states for all single-qubit states with a fixed nz.

Theorem 2For all single-qubit states with a fixed value nz,the coherence measures Cl1,Crand Cαhave the same ordering,where α=1/2,2.

The proof is easy based on the Proposition 2.Theorem 2 gives another sufficient condition that these three coherence measures have the same ordering.For any two single-qubit states,if they have the same value nz,then Cl1,Crand Cα(α =1/2,2)take the same ordering for these two states.In fact,we find the above result is also valid for other α ∈ (0,1)∪(1,2]by numerical method in Fig.1.

4 High-Dimensional States

In this section,we consider quantum states in a ddimensional quantum system.In Refs.[19]and[20],authors have shown that these coherence measures do not generate the same ordering for all states in a d-dimensional quantum system.Here,we show that they will generate the same ordering when we restrict to some special cases.

4.1 Pure States

We show these coherence measures generate the same ordering for some special pure states in a d-dimensional quantum system.We first introduce the notion of Shurconcave function.[41]For two vectorsandwe say thatis majorized bydenote it byif the rearrangement of the components ofandy1≥ y2≥ ···≥ yn,satisfieswhere k∈{1,2,...,n}.We say two vectorsandsatisfy majorization relation ifThe function F:Rn→ R,is called Schur-convex ifimpliesFunction F is called Schur-concave if −F is Schur-convex.

Lemma 1[41]Letbe a real value function,where A⊂Rdis permutation-invariant,and assume that the first partial derivatives of F exist in A.Then F is Schur-convex if and only if the inequalityholds on for each i,j∈{1,...,d}.Function F is Schur-concave if the inequality is reversed.

According to above lemma,it is easy to show the following proposition.

Proposition 3Equations(18),(19),(20)are Schurconcave functions,where α ∈ (0,1)∪ (1,2].

According to the above proposition,we can easily obtain the following theorem.

Theorem 3Let S be a set of pure states in a ddimensional quantum system(d∈Z+and d≥3),if any two pure states

satisfy majorization relation,then Cl1,Cr,Cαhave the same ordering for all states in S.

Theorem 3 gives a sufficient condition whether these coherence measures generate the same ordering for a set of pure states in a d-dimensional quantum system.But the following example will show that the inverse result does not hold.Two qutrit pure states are given as follows,

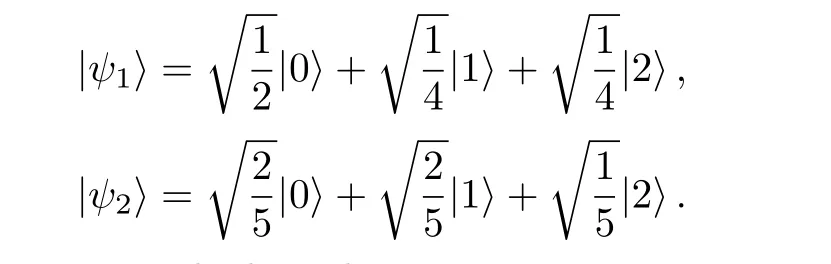
It is easy to calculate that

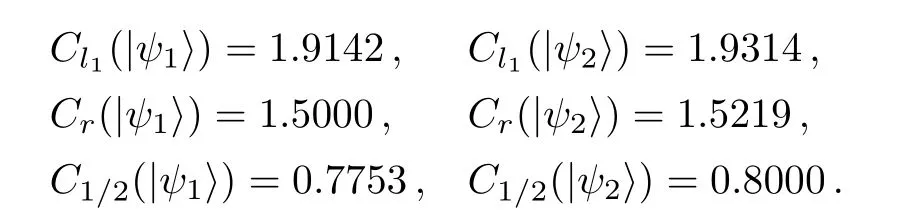
So

4.2 X States

Quantum states having “X”-structure are referred to as X states.Consider an n-qubit X state given by

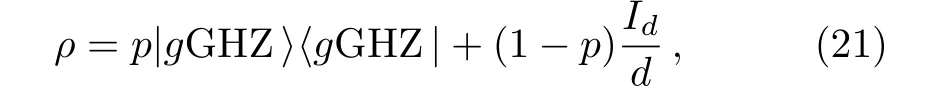
It is easy to calculate that eigenvalues of ρ are λ1=and their eigenvectors areSubstituting the eigenvalues and eigenvectors into the Eqs.(1),(2),and(4),we have l1norm of coherence

Relative entropy of coherence

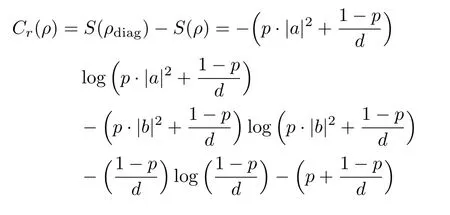
Tsallis relative entropy of coherence

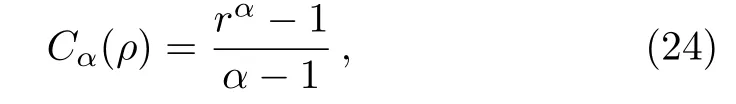
where

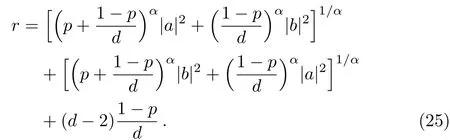
Substituting ρ into Eq.(6),we obtain the mixedness of the X state M(ρ)=p.Due to Eqs.(22),(23),(24)depend on|a|and|b|,we could assume a,b are nonnegative real number.Since|a|+|b|=1,then we have a,b∈[0,1].We assume a≤b,then a∈[0,1/2],otherwise,we can swap the roles of a and b if a≥b.

Proposition 4Given a fixed value p,Eqs.(22),(23),(24)have the same monotonicity with respect to a for a∈[0,1/2].

According to Eq.(22),it is obvious that0 for a∈[0,1/2].We consider the derivation of Crwith respect to a,

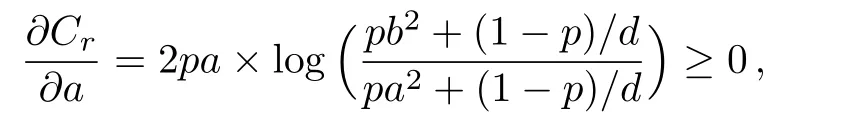
then it follows that Cl1,Crare decreasing functions with respect to a.

Before considering the monotonicity of Cα(Eq.(25)),we first consider the monotonicity of r with respect to a,

It is easy to show

hence, ∂r/∂a ≥ 0 for α ∈ (1,2],and ∂r/∂a ≤ 0 for α∈[0,1).Substituting these results into Eq.(24),we obtain ∂Cα/∂a ≥ 0 for α ∈ [0,1) ∪ (1,2]. Therefore,Cαis an increasing function with respect to a for any α∈(0,1)∪(1,2].

In the following,we will show that the result of Theorem 1 is also valid for all n-qubit X states with the fixed mixedness.

Theorem 4For all n-qubit X states with a fixed mixedness M=p,coherence measures Cl1,Cr,and Cαwill take the same ordering,where α ∈ (0,1)∪(1,2].

5 Dynamics of Coherence Ordering Under Markovian Channels

In this section,we discuss dynamics of coherenceinduced ordering under Markovian channels for singlequbit states.Here,we only consider amplitude damping channel.In fact,we can consider other Markovian channels by a similar method.Amplitude damping channel(ADC)can be characterized by the Kraus’operators

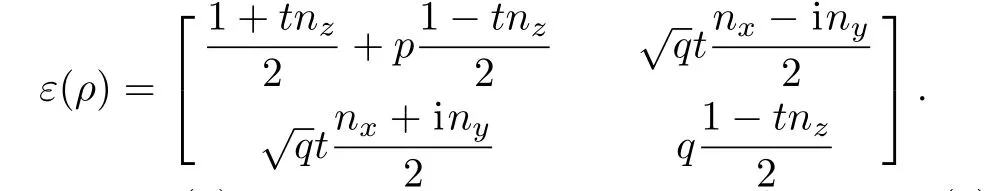
The state ε(ρ)can be represented by the form Eq.(8).The parameters are

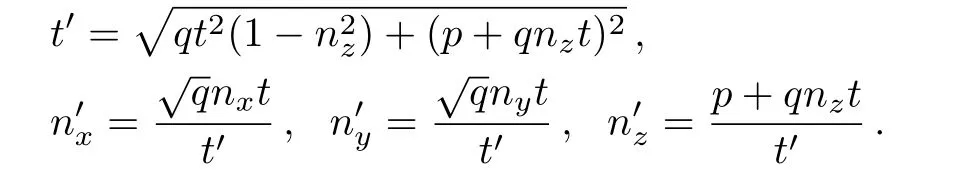
Substituting these parameters into Eqs.(13),(14),(15),we obtain

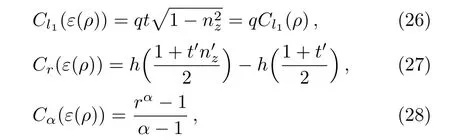
where

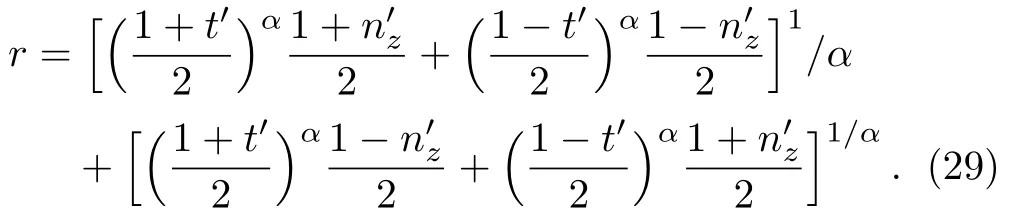
In accordance with Eq.(26),the amplitude damping channel does not change the coherence ordering induced by the l1norm of coherence for the single-qubit states.In the following,we will use the numerical method to discuss dynamics of coherence ordering with Crand Cαunder the amplitude damping channels for single-qubit states.

Let p=1/2,considering a special case of α=2,For the other case,similar discussions can be made.As presented in Figs.2 and 3,we know Cr(ε(ρ))and C2(ε(ρ))are not monotonic functions with respect to nzfor a fixed valued t.By Theorem 1,we know amplitude damping channel changes the coherence-induced ordering by Cror C2for all states with fixed mixedness.As presented in Fig.4,Cr(ε(ρ))and C2(ε(ρ))are increasing functions with respect to t for any fixed nz.By Theorem 2,we know that amplitude damping channel does not change the coherence-induced ordering by Cror C2for all single qubit states with fixed valued nz.

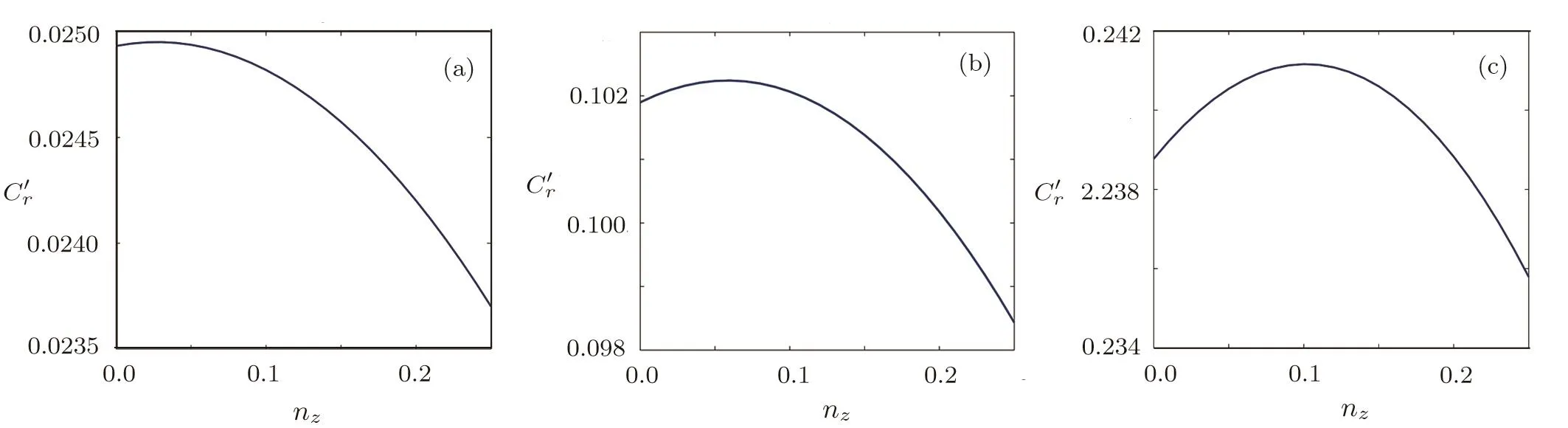
Fig.2 For fixed p=1/2,Cr(ε(ρ))are not monotone function with respect nzfor fixed(a)t=1/4,(b)t=1/2,(c)t=3/4,whererepresents Cr(ε(ρ)).

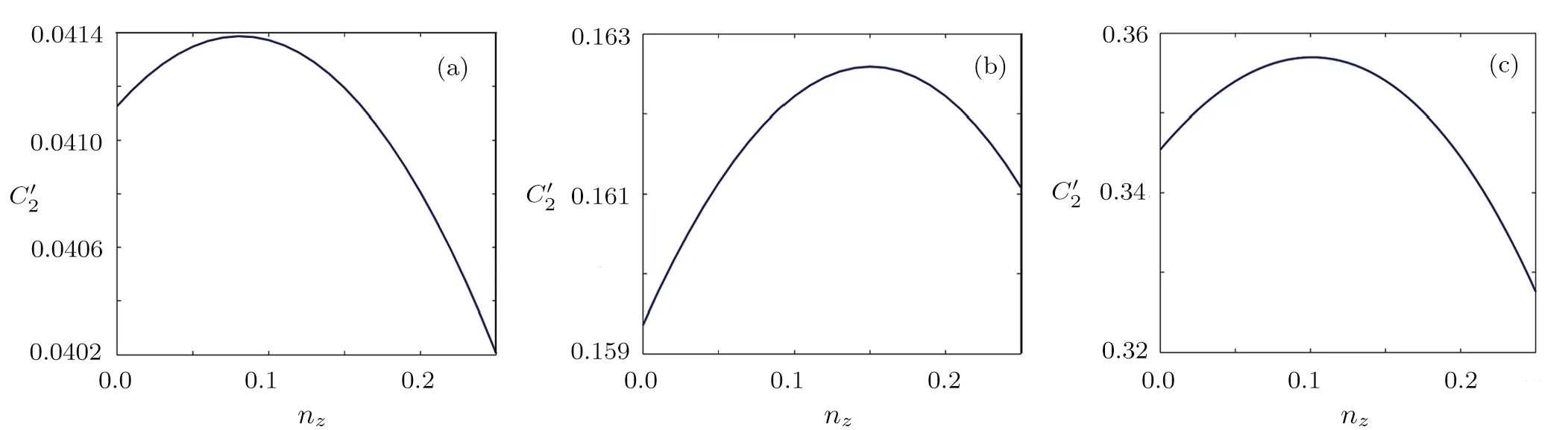
Fig.3 For fixed p=1/2,C2(ε(ρ))are not monotone function with respect nzfor fixed(a)t=1/4,(b)t=1/2,(c)t=3/4,whererepresents C2(ε(ρ)).

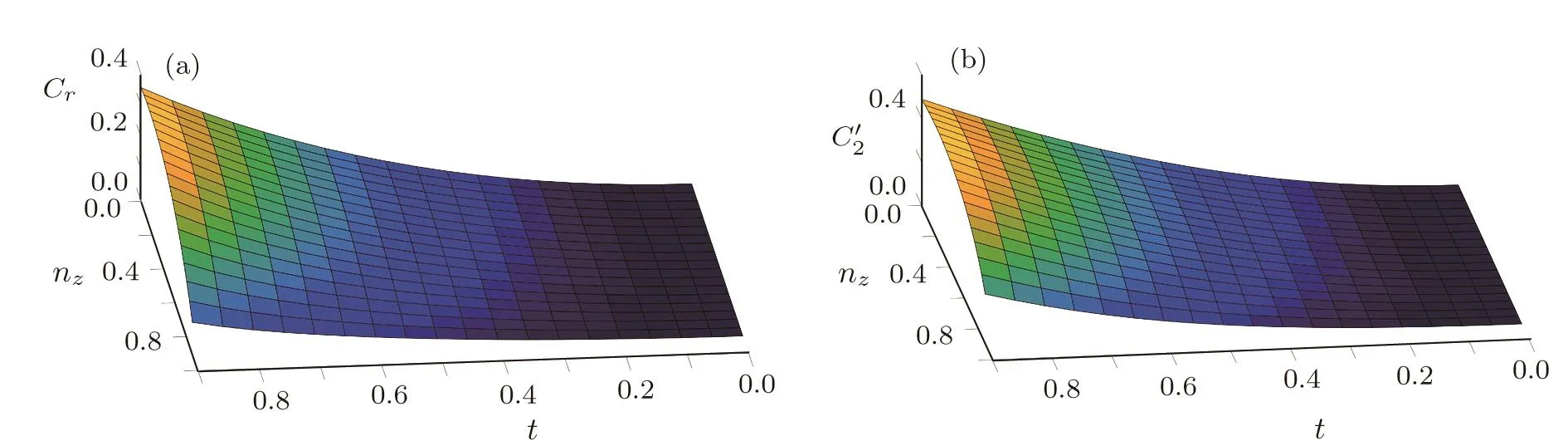
Fig.4 For fixed p=1/2,the variation of Cr(ε(ρ))and C2(ε(ρ))with respect to t and nzunder phase damping channel,whererepresents represents C2(ε(ρ)).

6 Conclusion

In this paper,we studied coherence-induced state ordering with Tsallis relative entropy of coherence,relative entropy of coherence and l1norm of coherence.First,we showed that these three measures give the same ordering for single-qubit states with a fixed mixedness or a fixed nz.Second,we considered some special cases of high dimensional states.We showed that these three measures generate the same ordering for the set of high dimensional pure states if any two states of the set satisfy majorization relation.Moreover,these three measures generate the same ordering for all X states with a fixed mixedness.Finally,we discussed dynamics of coherence-induced ordering under Markovian channels.We found the amplitude damping channel changes the coherence-induced ordering for single-qubit states with fixed mixedness.We can consider other Markovian channels by a similar method.

There are many further discussions need to be solved.For the other coherence measures,we can discuss their sufficient conditions of the same state order induced by coherence.We only considered dynamics of coherenceinduced ordering under special Markovian channels.Dynamic of coherence-induced ordering under any incoherent operator[9](Strictly incoherent operation and Maximally incoherent operation[31])is also an interesting subject for future work.