Solitons on a Periodic Wave Background of the Modified KdV-Sine-Gordon Equation∗

Ji Lin(林机), Xin-Wei Jin(金新伟),Xian-Long Gao(高先龙),and Sen-Yue Lou(楼森岳)

1Department of Physics,Zhejiang Normal University,Jinhua 321004,China

2Faculty of Science,Ningbo University,Ningbo 315211,China

AbstractThe Bäcklund transformation(BT)of the mKdV-sG equation is constructed by introducing a new transformation.Infinitely many nonlocal symmetries are obtained in terms of its BT.The soliton-periodic wave interaction solutions are explicitly derived by the classical Lie-group reduction method.Particularly,some special concrete soliton and periodic wave interaction solutions and their behaviours are discussed both in analytical and graphical ways.

Key words:soliton with periodic wave interactive solution,nonlocal symmetry,Bäcklund transformation,mKdV-sG equation

1 Introduction

With the more applications of soliton theory in the diverse fields of physics including nonlinear optics,plasma physics and condense matter physics and so on,[1−2]to explore new explicit solutions of the nonlinear differential equations(NPDE),which are widely applied in physics is an amazing and important research work.There were many useful methods such as the Darboux transformation(DT),Hirota’s bilinear method,and Bäcklund transformation(BT)to obtain multi-soliton solutions of integrable NPDEs[3−5]from simple constant solutions.Recently,new solitons and multi-soliton complexes moving on the cnoidal wave in the coupled nonlinear Schrödinger equation(NLSE)and the defocusing NLSE by using the DT[6]and more exact interaction solutions among solitons and other complicated periodic functional waves including the Jacobi elliptic functions and Painlevé waves by the nonlocal symmetry reduced method and the BT[7]were constructed.This nonlocal symmetry reduced method has successfully been applied to many integrable NPDEs such as KdV,KP,sine-Gordon(sG),NLS and Konopelchenko-Dubrovsky(KD)equations for analytical solitons interaction solution with the background governed by the Jacobi elliptic functions and the third type of incomplete elliptic integrals.[8−11]

The(1+1)-dimensional modified Korteweg-de Vriessine-Gordon(mKdV-sG)equation

can govern many physical phenomena.In Eq.(1),these coefficients(c1,c3)and c2are related to the dispersion and nonlinearity of the media.[12]The propagation and interaction of few-cycle pulses(FCPs)in the self-focusing Kerr nonlinear optics media,which exists both high-and lowfrequency resonances can be described by the mKdV-sG equation(c1=1)in Eq.(1).[13]This general mKdV-sG equation(1)can be considered to model the generation of supercontinuum with an initial high-intensity ultrashort pulse in gas- filled hollow waveguides.[14]The general mKdV-sG equation(1)is not completely integrable unless its coefficients is satisfied such as c3=(3/2)c2.[15]For this case,the mKdV-sG equation(1)is integrable and has N soliton solutions obtained by the Hirota method.[16]A systematic construction of soliton solutions with an arbitrary time-dependant function is provided by the dressing method.[17]And formally several exact distinct solitary solutions for the mKdV-sG equation are derived by using the variable separated ODE method.[18]Meanwhile,the mKdV-sG equation can be reduced to the mKdV equation(or the sG equation)if c1=0(or,c2=c3=0).When the resonance frequency of atoms in the physical system is well above or well below the characteristic duration of the pulse,the propagation is described by the mKdV or sG equation,respectively.

The investigation of the nonlocal symmetries has attracted great attentions of many mathematical physicists.The nonlocal symmetries can be obtained by the algorithmic approach,inverse recursion operators,Möbius(conformal)invariant form,DT,BT,nonlinearizations,selfconsistent sources,etc.[7,19−23]In Ref.[7],nonlocal symmetries of the pKdV equation are derived from its BT and exact soliton interaction solutions with periodic functions are revealed by the similarity symmetry reduction method.Here,we will find soliton-periodic wave interaction solutions of the mKdV-sG equation(1)by the nonlocal symmetry reduction method,which is proposed by Lou.[7]By leting ψ=2i lnu and c2=(2/3)c3=1,we can transform the mKdV-sG equation(1)into the following equation

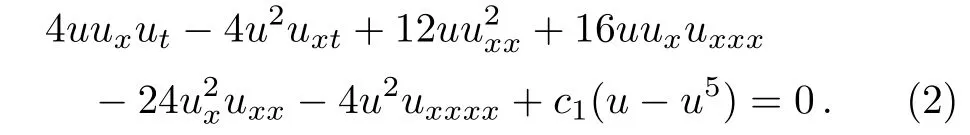
We can derive the BT of Eq.(2)as

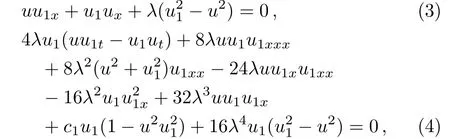
in which λ is an arbitrary parameter.According to the compatible condition u1xt=u1tx,u1must be satisfied the mKdV-sG equation(1)if u is a solution of Eq.(1).In Sec.2,from the BT equations(3)–(4),we obtain new nonlocal symmetries of Eq.(2)and infinitely many local symmetries by extending the mKdV-sG system because there is a parameter λ included in nonlocal symmetries.In Sec.3,by solving the initial value problem of finite symmetries of the extended system, finite symmetry transformation and explicit solutions are obtained.In Sec.4,similar reduction equations are derived by the classical Lie-group reduction method.Soliton interaction solutions moving on periodic waves are constructed.The last section is a short conclusion and discussion.

2 Nonlocal Symmetries of the mKdV-sG Equation(2)

Symmetries of a PDE are any solutions of linearized equation generated from the requirement that the form of this PDE is invariant under an infinitesimal transformation.According to the nonlocal symmetry reduction method,[7]we can construct nonlocal symmetries of the mKdV-sG equation(2)through to find some symmetries of the BT(3)–(4).The form of the mKdV-sG equation(2)is invariant under infinitesimal transformations

where ϵ is an infinitesimal parameter. The symmetry equations of the mKdV-sG equation(2)and BT(3)–(4)can be written as

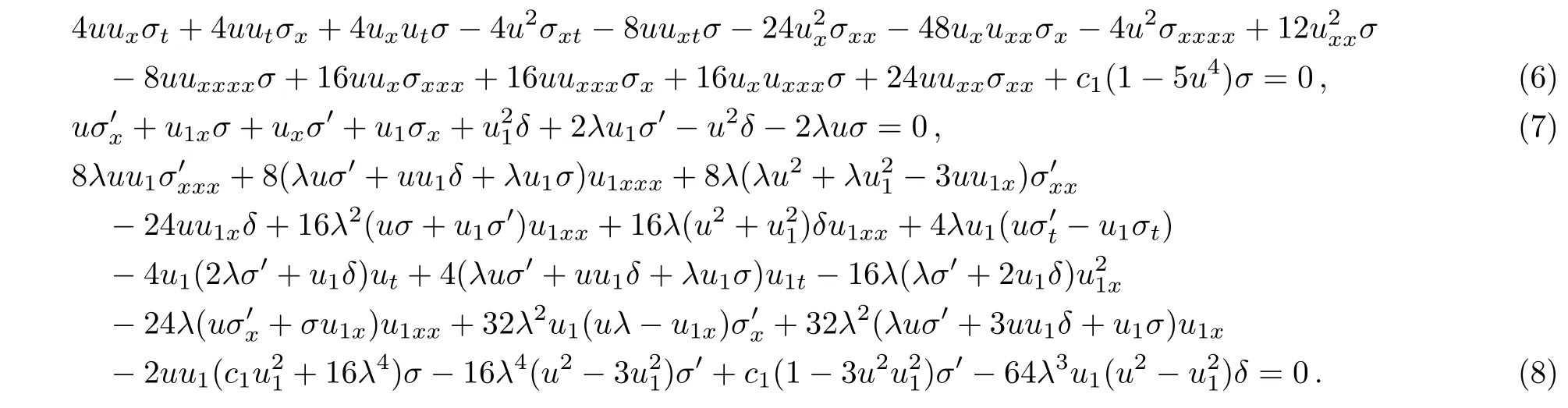
Obviously,these symmetries equations(6)–(8)are very complicated.So,it is very difficult to derive the general solutions of these symmetries.Here,we only discuss the special solutions of Eqs.(6)–(8).We obtain the nonlocal symmetry σ in the case of σ′=0 and δ=0.Substituting σ′=0 and δ=0 into Eq.(7)and integrating Eq.(7)two times with respective to x,we obtain the nonlocal symmetry of the mKdV-sG equation(1)is the form

where f is satisfied

It is obvious that the consistent condition fxt=ftxis satisfied with the BT(3)–(4).

As we know,nonlocal symmetries can not be directly applied to reduce the differential equations(DEs).Hence,we have to transform nonlocal symmetries of the mKdV-sG equation(2)into local ones,especially into Lie-point symmetries.In order to derive local symmetries from nonlocal ones,we need to introduce some additional dependent variables to extend the mKdV-sG equation(2)to a closed prolonged system.As long as we introduce only two dependent variables f=f(x,t)and g=g(x,t),the closed prolonged system is constructed as

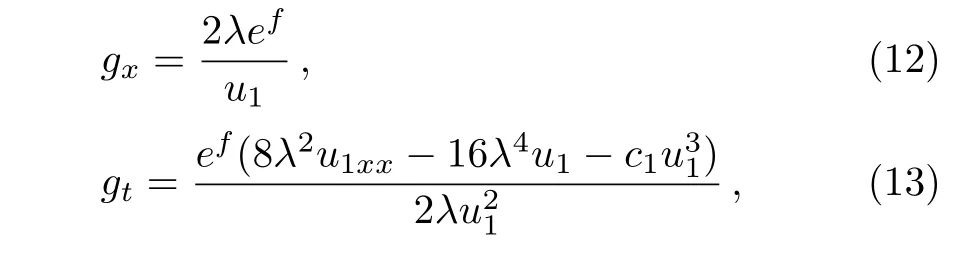
with Eqs.(10)and(11).It is not difficult to derive their local symmetries of the closed prolonged system(10)–(11)and(12)–(13)

where f and g are dependent on the solutions u and u1of the mKdV-sG equation(2).

3 Finite Symmetry Transformation and Explicit Solutions

The extent prolonged mKdV-sG system including Eqs.(2),(10),(11),(12),and(13)has the Lie-point sym-metry vector

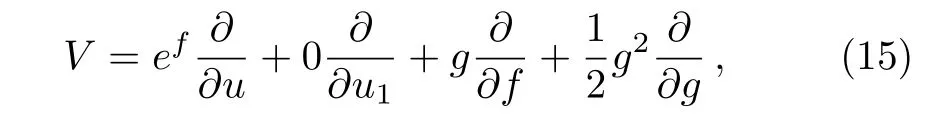
and the corresponding initial value problem is

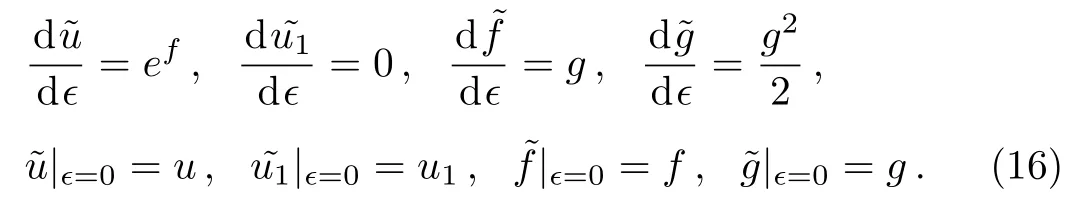
By solving the above initial value problem(16),the finite transformation of the prolonged system can be obtained

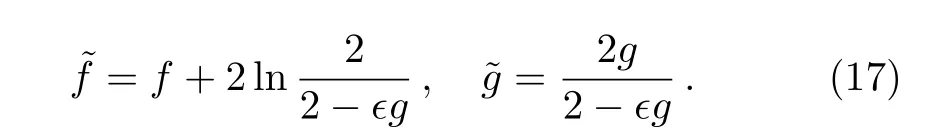
This finite transformation(17)means that a new solution will be derived from the known solution of the mKdV-sG equation(2).Actually,this new solution is the third one because the second solution of the mKdV-sG equation(2)can be obtained from the known one by the BT(3)–(4).The finite transformation(17)is just the Levi-transformation.[24]Here,we give a simple example to illustrate.We select the initial solution u=1 of the mKdV-sG equation(2)and obtain the initial special solutions of the prolonged system(3),(4),(10),and(11)are

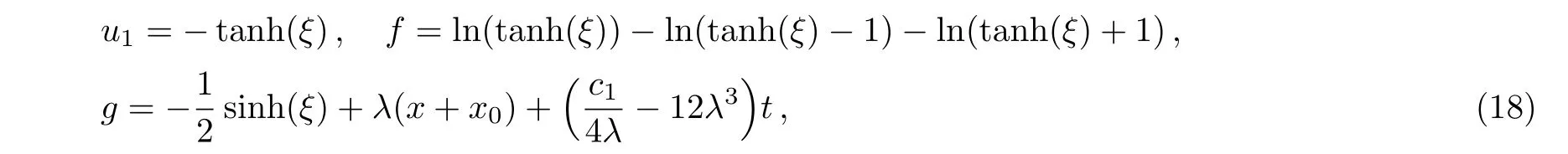
where ξ=(4λ3+c1/4λ)t− λ(x − x0),x0and λ are arbitrary constants.Inserting Eq.(18)into the finite transformation(17),the new solution of the mKdV-sG equation(2)has the form

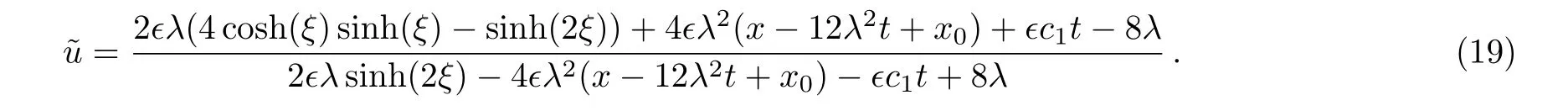
4 Lie Point Symmetry Reduction of the Prolonged System

The classical Lie-group reduction method is one of the most useful ones to find explicit solutions of integrable or non-integrable partial differential equations.[25−27]In this section,we have to linearize the closed prolonged system(2),(7),(8),(10),(11),(12),and(13)by the infinitesimal transformation

Then,we construct Lie-point symmetries have the following form

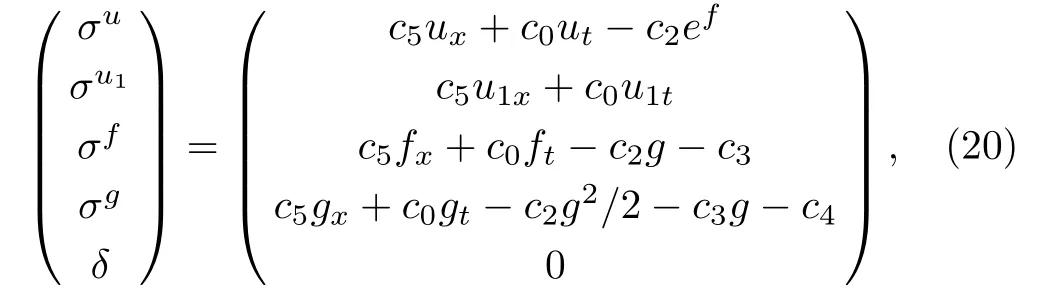
in which c0,c2,c3,c4,and c5are arbitrary constants.The finite transformation(17)is the special case of Eq.(20)by taking c0=c3=c4=c5=0 and c2=1.

According to the classical Lie-group reduction method,we are able to give some similar reduction ordinary differential equations(ODEs)by solving symmetry constraint conditions σi=0(i=u,u1,f,g)and δ=0 in Eq.(20),that means to solve the characteristic system

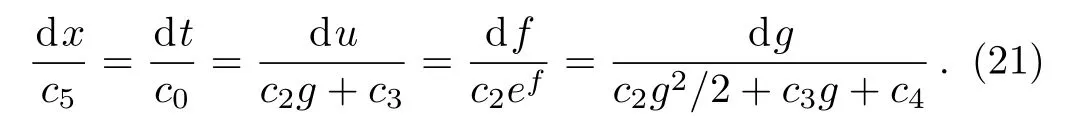
To find new similarity reduction solution of the mKdV-sG equation(2),it is requested thatWe can obtain two non-trivial similarity reductions.

Case 1and

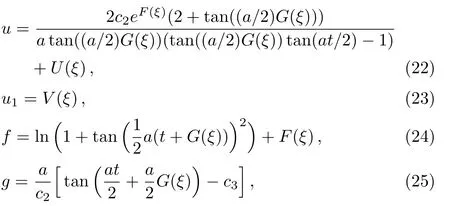
by solving Eq.(21). Substituting Eqs.(22)–(25)into the prolonged system,the corresponding group invariants U(ξ),F(ξ),G(ξ),and V(ξ)are satisfied four reduction equations

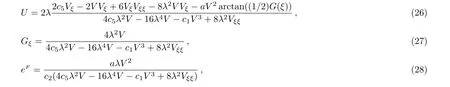
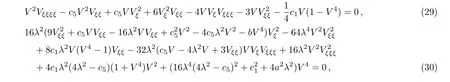
where ξ=x−c5t.The group invariant V should be satisfied Eqs.(20)and(30).We can derive analytical expressions of other group invariants U,F,and G from Eqs.(26),(27),and(28)if we obtain exact solution of the invariant function V from Eqs.(29)and(30).

Case 2and

For this case,we derived the invariant solution

These invariants U,V,F,and G are functions of the group invariant variable ξ=x−c5t and have forms

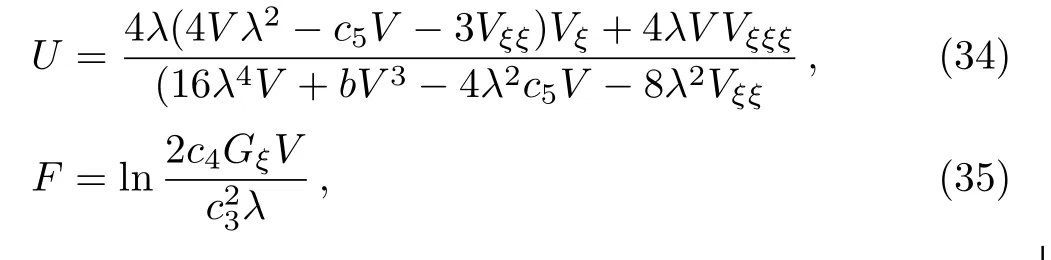
and V still satisfies Eqs.(29)and(30).Finally,the solution(31)of the mKdV-sG equation(2)is obtained from Eqs.(34),(35),and(36)with the solution V of Eq.(29)and(30).

5 Interaction Solutions of Soliton and Jacobi Functions

Apparently,by constructing some special solutions of Eqs.(29)and(30)and solving the similar reduction equations(26),(27),and(28),we successfully derive some new explicit solutions of the mKdV-sG equation(2).Here,we show four solutions expressed by the Jacobi elliptic functions for Eqs.(29)and(30)as examples.And five interaction soliton with periodic function solutions of the mKdV-sG equation(2)are shown as follows.

Case 1Taking

we can obtain the function V(ξ)is

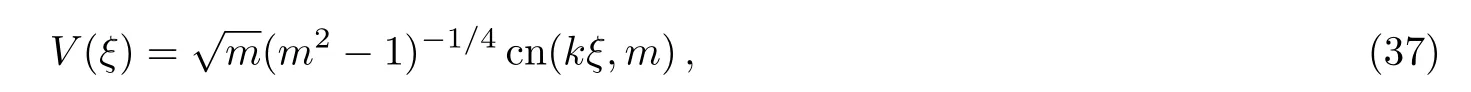
from Eqs.(29)and(30).Then,one soliton-Jacobi elliptic periodic wave solution of the mKdV-sG equation(2)is derived

where

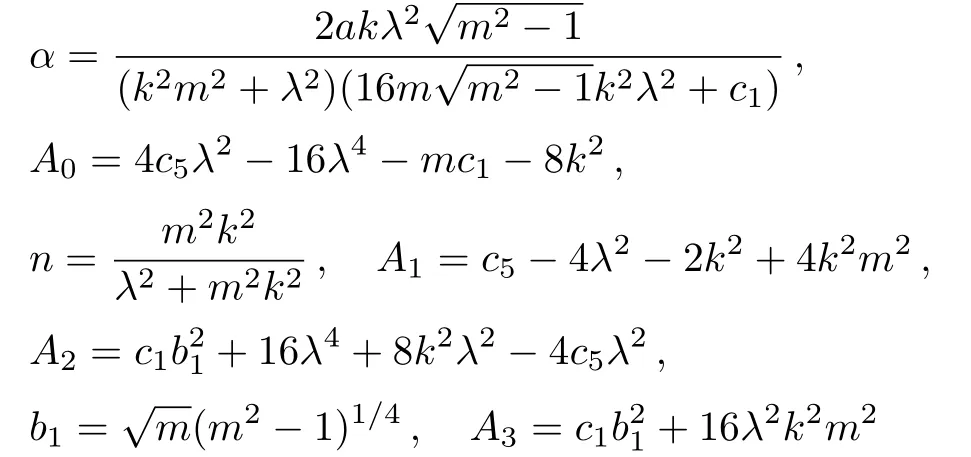
and the third type of incomplete elliptic integral function

Figure 1 shows that the interaction of a kink soliton with cnoidal wave solution(38)by fixing parameters

Figure 1(a)displays the evolution of the interaction between a kink soliton and the traveling cnoidal wave in the(1+1)-dimensional space-time plane.Figures 1(b)–1(d)reveal the evolutions of the kink-periodic wave solution(38)along time t with x=−5,x=0,and x=5,respectively.From Fig.1,we understand that the traveling cnoidal periodic wave has a half wave phase shift after the interaction with the kink soliton at t=0.

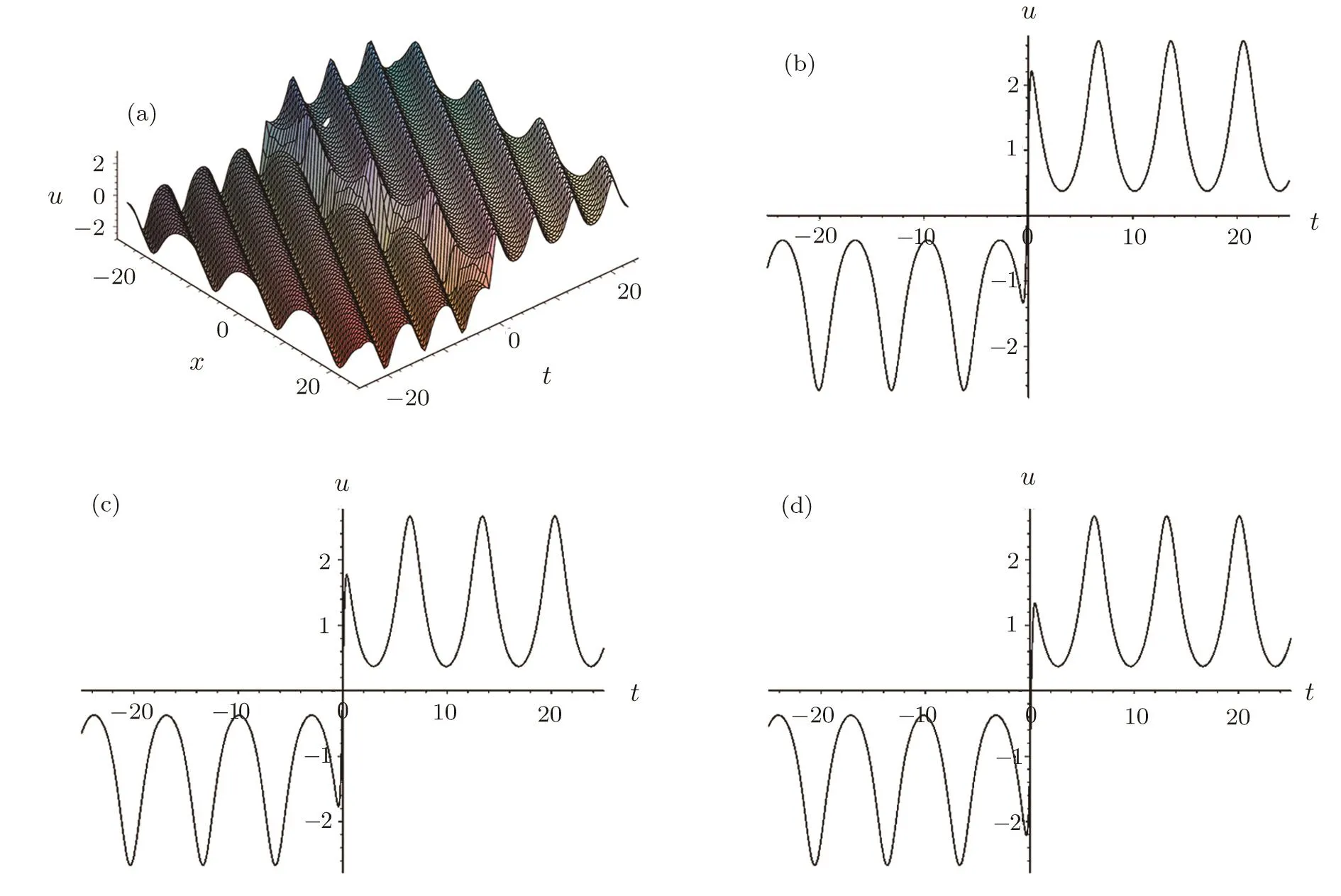
Fig.1 The propagation of a kink soliton with the Jacobi elliptical wave solution(38),(a)the evolution of u,(b)x=−5,(c)x=0,(d)x=5.

Case 2If parameters are taken as

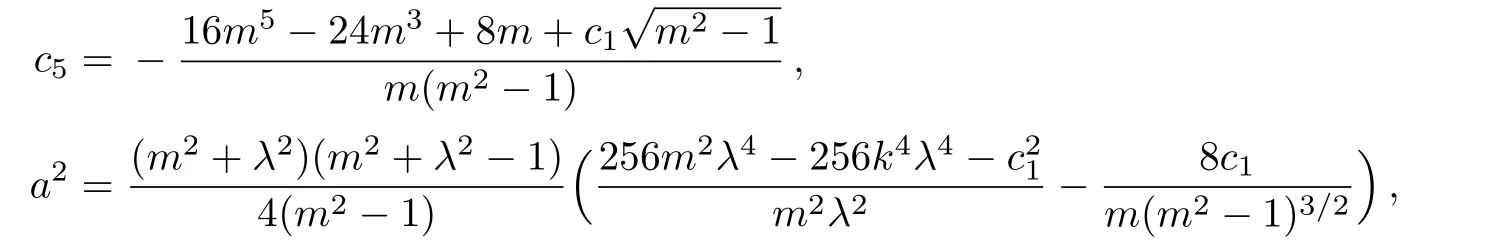
the function V(ξ)is derived from Eqs.(29)and(30)

And the second solution of the mKdV-sG equation(2)is

where

Case 3If we take the parameters as

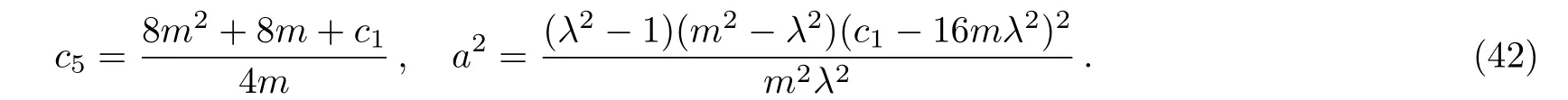
The solution of Eqs.(29)and(30)is a simple form

and the third soliton and periodic wave interaction solution is

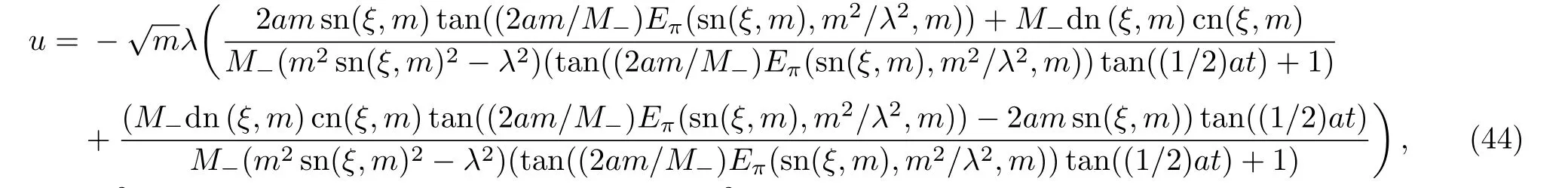
Case 4We take

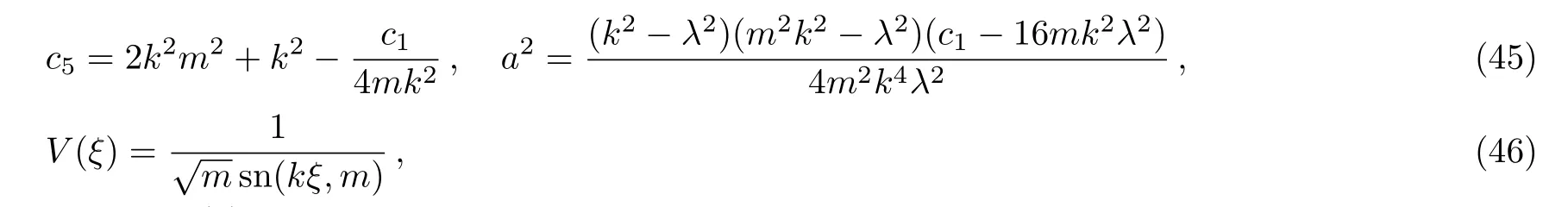
then,the fourth solution of Eq.(2)is

Figure 2(a)is the density plot of the interaction of a dark soliton with the periodic wave.It is clear that the phase shift of the cnoidal periodic wave happens when it interacts with the dark soliton.Their interaction is an elastic collision.

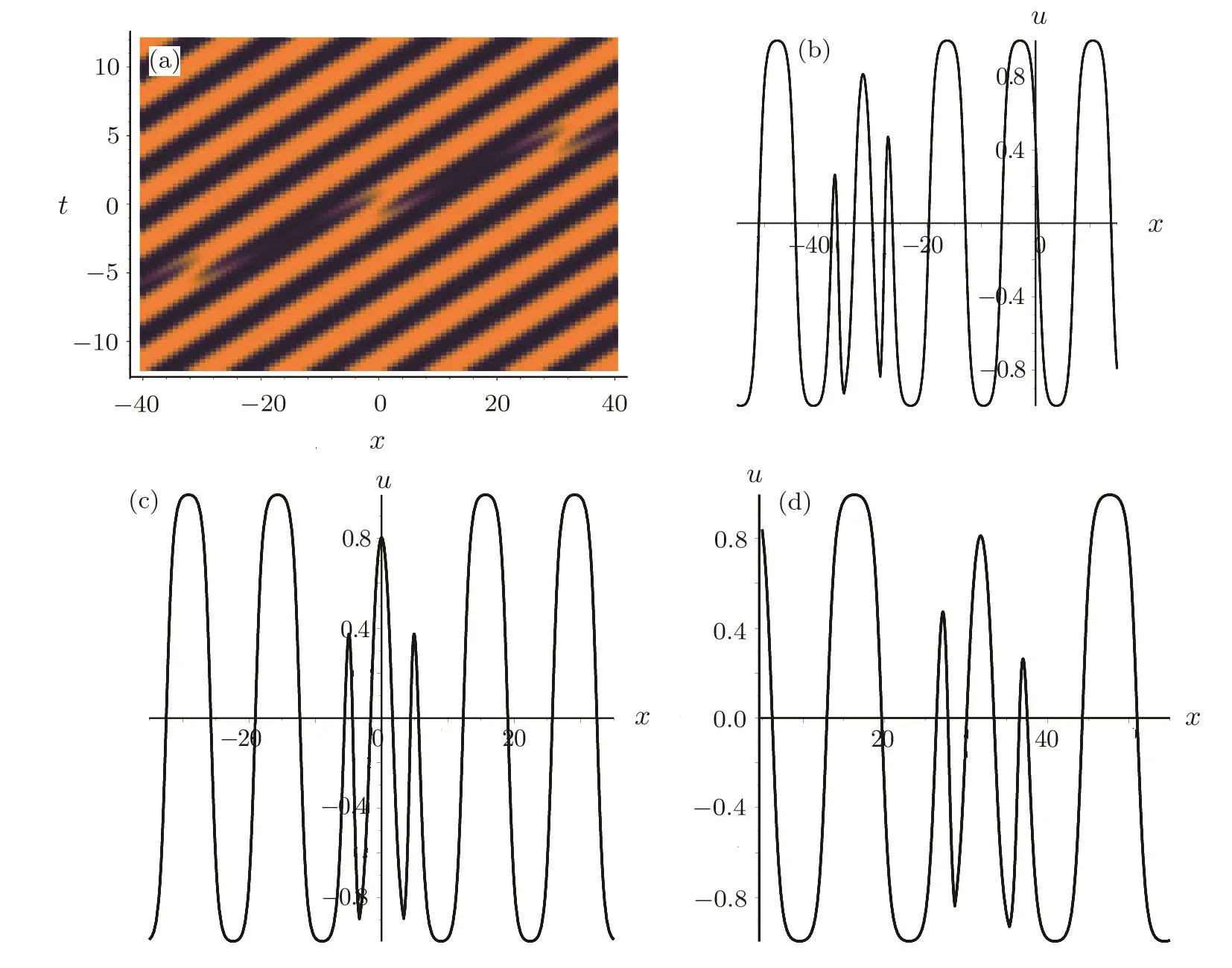
Fig.2 (a)The three-dimensional plot of the interactions between a dark soliton and a cnoidal wave expressed by Eq.(47)with Eq.(48).And a dark soliton with a periodic wave interaction graphs at the propagating times(b)t=−5,(c)t=0,(d)t=5.

Case 5Taking

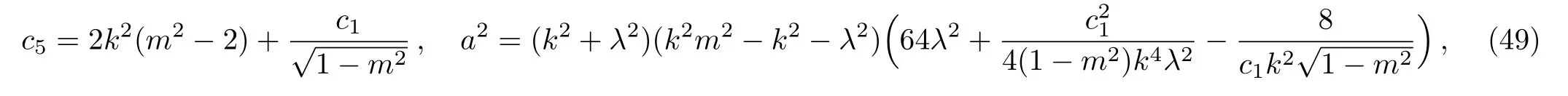
the function V(ξ)is

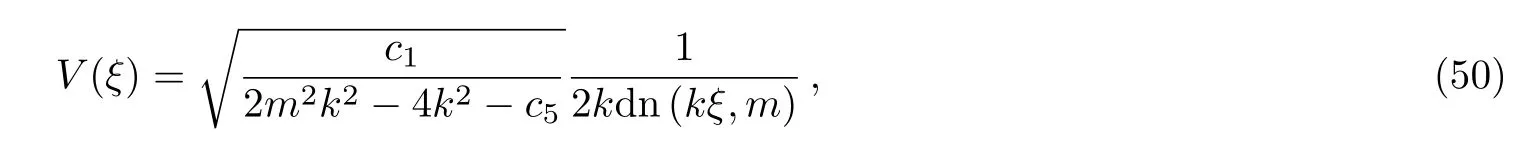
and the fifth type of a soliton with a periodic wave interaction solution for the mKdV-sG equation(2)is

where

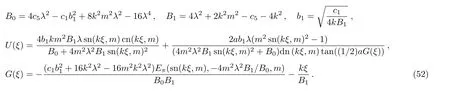
Fig.3 The propagation of an anti-kink soliton with the Jacobi elliptical wave solution(51)(a)The evolution of u,(b)t=−5,(c)t=0,(d)t=5.

Figure 3 describes that the interaction of an anti-kink soliton with a cnoidal periodic wave given by Eq.(51)and the parameters are fixed by

c1=−1.0,k=0.5,λ=1.0,m=0.9,c0=0.5.(53)This interactional property is exactly the same as those of the kink(or dark)soliton with the cnoidal waves shown as in Fig.1(or Fig.2).

6 Conclusions

In conclusion, firstly,we construct the BT of the mKdV-sG equation(2)and calculate nonlocal symmetries of the mKdV-sG equation(2)with its BT.Secondly,the extended prolonged system is constructed by introducing two dependent variables.The finite symmetry transformation of the closed prolonged system(2)and(10)–(13)by the initial value problem is acquired and some explicit solutions of Eq.(2)have been obtained.Furthermore,two similarity reduction equations are obtained by the classical Lie-group reduction method.By solving these complicate reduction equations,various types of soliton-cnoidal wave interaction solutions are derived.As examples, five explicit solutions of interaction soliton with cnoidal wave are revealed.And the evolutions of a kink,a dark and an anti-kink with the cnoidal wave interactions are displayed in Figs.1,2,and 3,respectively.These interactions of three types of solitons(kink,anti-kink and dark)with the cnoidal wave are elastic though the phases are shifted after the collisions of between solitons and cnoidal waves.The general mKdV-sG equation(1),which coefficients have satisfied the condition is completely integrable.Various kinds of soliton solutions of the mKdV-sG equation have been derived by different methods.While,soliton-cnoidal wave interaction solutions are not easy to be obtained by other traditional methods such as the bilinear method,DT and so on.However,these soliton-cnoidal wave interaction solutions are able to be obtained by the consistent Riccati expansion and tanh expansion methods and the truncated Painlevé expansion approach.[28]