三角高程测量精度研究及实践

2018-08-02曾志敏

机械管理开发 2018年7期

曾志敏

（大同煤矿集团华盛虎峰煤业有限公司，山西河津 043302）

引言

1989年颁布的《煤矿测量规程》（以下简称《规程》）中部分内容已经难以适应现有测量仪器的升级换代和发展，并且有许多测量方法与实际情况不符，阻碍了实际测量技术的发展。因此，探讨如何实现高精度的矿井测量方法，不断提高矿井测量精度，可为研究矿井测量精度提供实际的依据。

1 三角高程井下测量理论存在的误差分析

1.1 参数选择误差

仪器为SET5F型防爆全站仪。该仪器能够对三维坐标进行测角、测距、数据传输以及存储记录，其可以被用于井下的高程控制以及平面控制的测量。其所具备的两个主要的技术指标是测距精度和测角精度。在测量导线的过程中，不对觇标高v以及仪器高i进行量取，而是直接通过仪器基座的高差来传递高程。这就可以不在误差分析中考虑觇标高v以及量取仪器高i的影响，也就是mv=mi=0。

1.2 观测高差理论当中的误差测定原理

在对相邻两个点之间的高差h进行测量的时候，可以根据公式（1）计算：

式中：L为实际测得的斜长；i为仪器高；δ为垂直角；H为觇标高。

根据误差传播定律：

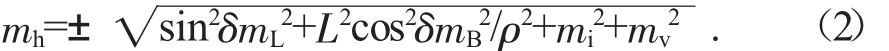
如果mv=mi=0，那么就可以将上式简化为：

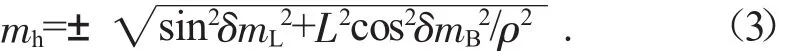
式中：mL为测边误差；mB为测角误差；ρ为常数，值为206 265。

根据公式（3）能够看到，随着垂直角的增大，在高差误差中，距离观测误差的影响也越来越大，而垂直角观测误差则在垂直角变大的过程中逐渐变小[1]。

使用上述测量仪器，并且采用上述测量方法，根据公式（3），对于0°～25°的不同垂直角以及30～100 m的不同边长进行测量，结果如表1所示。

表1 每一测站存在的观测高差中误差 mm

通过对表1当中所存在的数据的比较能够看出，随着边长的增加，观测高差中误差也随之增大。

2 井下实际三角高程测量精度分析

2.1 井下实际三角高程测量精度的评定

将三角高程测量闭合差的数据作为计算的标准，得到其每千米高程测量中误差mh0为：

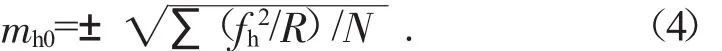
式中：fh为三角高程测量闭合差；N为闭合圈的个数；R为在三角高程测量当中闭合导线的长度，km[2]。

通过仪器先后测量了井下所有贯通工程闭合导线，测得出这些闭合导线的三角高程测量的高差闭合差之和∑（fh2/R）=5 293.55。带入公式（4）进行计算mh0，得到：

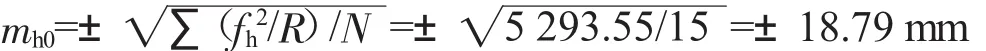
也就是说，在每千米的三角高程测量当中，所存在的高差中误差mh0=18.79 mm。

2.2 该矿实际三角高程测量精度与《规程》当中规定的精度比较

在《规程》当中，对于井下的三角高程测量高差闭合差的要求为±（L是导线的长度，km）。

在《规程》当中对每千米三角高程测量当中的高差中误差要求的是：

通过上述的计算能够看到，该矿的实际三角高程测量精度fh0=±18.79 mm，明显要高于《规程》当中限制的±50 mm。

2.3 该矿三角高程测量精度和理论误差的比较

三角高程测量每千米的理论高差误差应该处于7～9 mm之间，但是在实际测量当中，精度为mh0=18.79 mm，之所以会产生这一差距，分析其原因有：在对理论进行分析的过程中只是对偶然误差因素进行了考虑，忽略了系统误差的影响，并没有将觇标高以及量取仪器高考虑进来，在实际测量的过程中，需要每隔300～500 m就设置一组导线点，在导线点位置需要觇标高和量取仪器高，二者并没有完全消除。在实际测量过程中，并不是一个闭合导线就代表完成一次观测，每一个导线的分段都会影响量边、测角，并且在井下干扰观测的因素非常多，难以控制观测条件，这样也影响到量边、测角误差。

3 实例

在进行巷道施工中，为了保证其盘区能够顺利接替，选择两条不同的挂口位置掘进上山，即胶带上山以及中四轨道上山的方式。前期预计的贯通点K处于轨道上平落处，由于工期时间紧张，目前已经展开了铺轨工作。为了能够减少轨道贯通后的距离调整，降低工程返修损失，生产部门的相关人员将限制贯通点偏差为100 mm。目前，此工程的导线长度为2 200 m，上山倾角分别为13°以及18°。远程控制只能利用三角的测量方式[3]。利用《规程》中三角远程测量进行误差分析。一次独立中误差：mhk=mh0L倍中误差:mhk预=2mhk=±148 mm＞100 mm。由此可得，一次独立中误差不满足要求，需要进行二次误差预测，即±104 mm≈100 mm，大体上满足要求。