新型石膏混凝土复合外墙板的恢复力模型研究

姜 南 ，梁 壮

(1. 天津大学建筑工程学院，天津300072；2. 滨海土木工程结构与安全教育部重点实验室(天津大学)，天津300072)

新型石膏混凝土复合外墙板相较于传统的石膏混凝土速成墙板，其优势主要体现在两个方面：①在垂直石膏孔腔中设置水平石膏孔腔，并在水平方向设置钢筋．这样设置可以给节点处理带来极大的便利，同时有利于提高墙板的整体性；②增加外保温层，改善了墙体的节能性能，降低建筑能源消耗．近年来，国家和政府积极倡导绿色保温节能墙体材料在建筑住宅产业中的应用[1]，该新型墙板符合这一发展理念，具有一定的应用前景．

恢复力模型是进行结构弹塑性地震反应分析的重要基础．恢复力模型包括两部分：骨架曲线和滞回关系．目前，关于钢筋混凝土剪力墙的恢复力模型研究[2-4]较多，但大多是利用试验数据进行回归分析，无法直接应用．而一些经典的恢复力模型计算方法[5]，如 Fajfar剪切滑移模型、Ghobarah滑移模型、Ozcebe模型、Takeda模型及其修正模型等，有些不能模拟出反 S形滞回环特征，有些则适用性较差，不能直接应用于石膏混凝土复合墙板．

基于新型石膏混凝土复合外墙板的抗震性能试验，本文首先对骨架曲线的特征参数进行了理论推导和分析；然后建立外墙板的双参数损伤模型，利用该损伤模型提出了相应的滞回规则；最终得出基于损伤的恢复力模型，并进行了非线性验证．

1 试验概况

1.1 试验内容

为研究新型石膏混凝土复合外墙板在地震作用下的抗震性能，课题组对3个墙板构件进行了低周反复加载试验研究[6]．试件的平面图和尺寸分别如图1和图2所示．

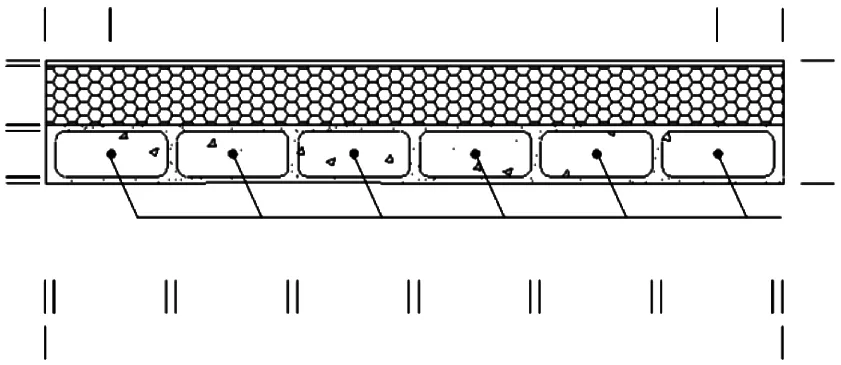
图1 试件平面图Fig.1 Plane graph of specimen

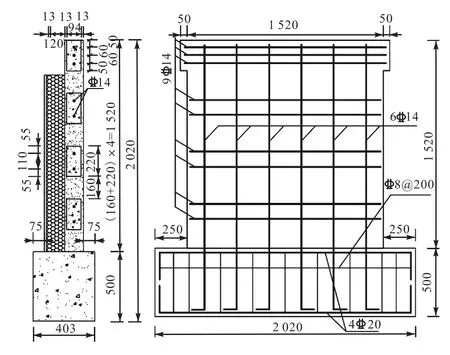
图2 试件立面图和配筋图Fig.2 Elevation and reinforcement diagram of specimen

1.2 试验结果

通过试验得到了3个试验构件的滞回曲线，如图3所示．由图3可知：

(1)滞回曲线有明显的捏缩现象，滞回环形状呈反 S形，这说明在加载过程中，构件出现了一定的剪切滑移现象，构件的破坏类型属于剪切破坏．

(2)在试件开裂之前，力与位移之间基本上呈线性变化，滞回环内部的面积几乎为 0，随着荷载的逐渐增加，墙板的刚度退化十分明显，滞回环的面积也逐渐增大，此时试件逐渐从弹性阶段进入弹塑性阶段．加载后期，在侧向荷载几乎不变的情况下，试件的侧向位移不断增大，此时说明构件完全进入塑性阶段，直到发生破坏．

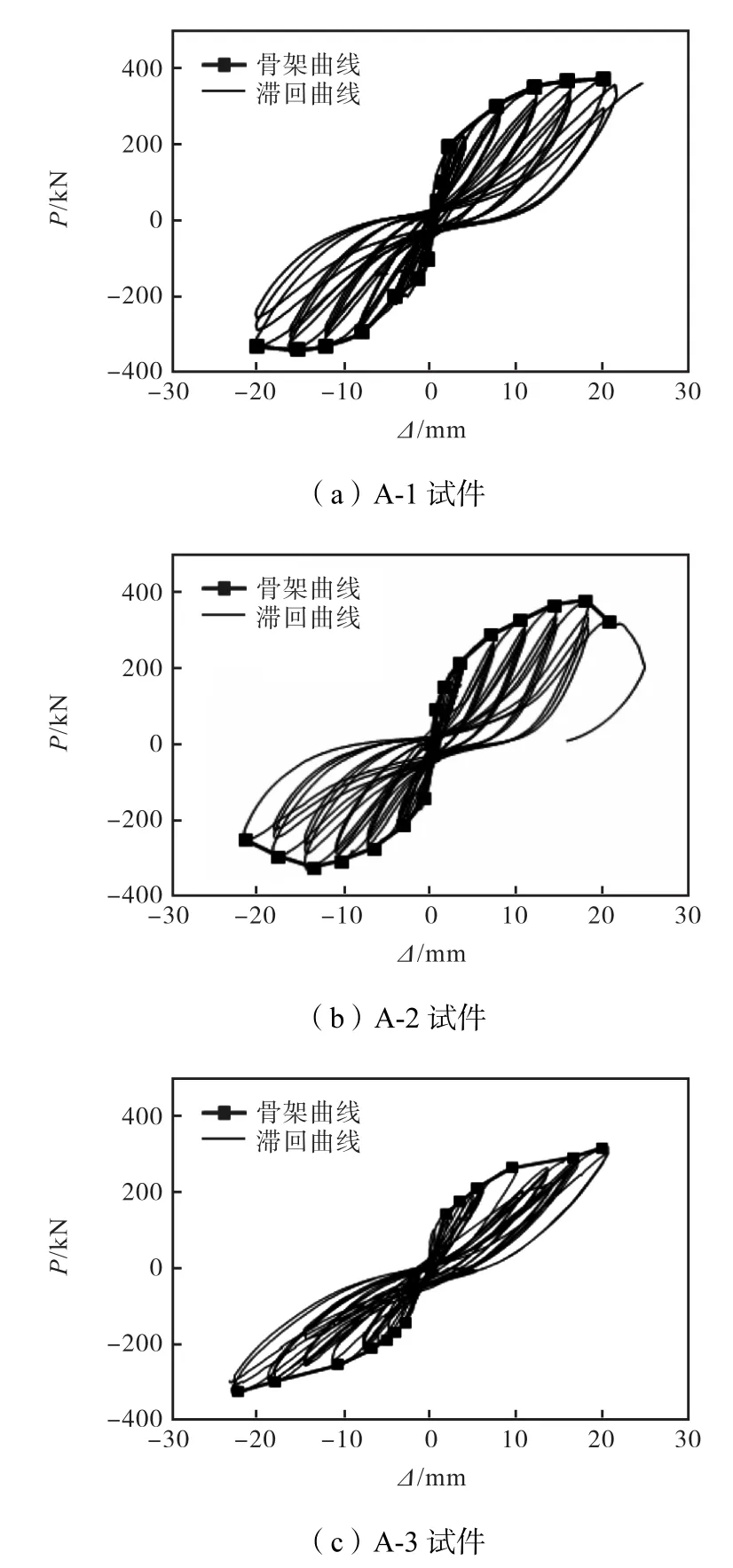
图3 荷载-位移滞回曲线与骨架曲线Fig.3 Load-displacement hysteretic curve and skeleton curve

2 骨架曲线的建立

2.1 骨架曲线模型的选取

新型石膏混凝土复合外墙板在加载过程中经历了开裂、屈服、硬化、破坏4个阶段．为准确地模拟试件的整个受力过程，本文选取考虑刚度退化的四线型模型，如图4所示．其中，A、B、C、D 4个特征点分别为开裂点、屈服点、峰值点和极限破坏点．

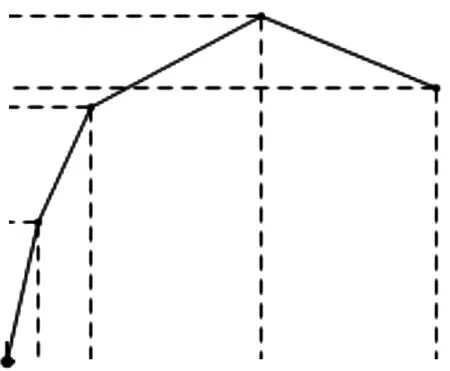
图4 骨架曲线模型Fig.4 Skeleton curve model

2.2 不同极限状态下的特征点计算

新型石膏混凝土复合外墙板在极限状态下的假定：①构件截面变形后仍为平面；②应变沿截面高度呈线性分布；③不考虑各材料之间的相对滑移；④混凝土芯柱部分由于混凝土横梁的连接作用，使得整体性大大增强，为简便计算，将该部分等效成一整块混凝土板，等效后的混凝土弹性模量为

式中：Eeq为等效后的混凝土弹性模量；Ec为试验构件的混凝土弹性模量；Vc为混凝土的体积；Vg为等效部分内的石膏体积．

2.2.1 开裂极限状态

1) 开裂荷载Pcr和开裂位移Δcr

在加载过程中，当荷载增加到开裂荷载Pcr时，构件截面受拉区边缘的纤维石膏恰好达到开裂应变，构件处于开裂极限状态．纤维石膏板由于有纤维的拉力作用，仍可承担拉应力，故考虑受拉区纤维石膏的拉力作用．其中，纤维石膏是指在建筑石膏粉中加入玻璃纤维作为增强材料而得到的一种建筑材料，这样处理的好处是能大大提高石膏板的抗拉性能．

构件截面的应力和应变分布如图5所示．根据截面平衡条件，建立相应的平衡方程，即

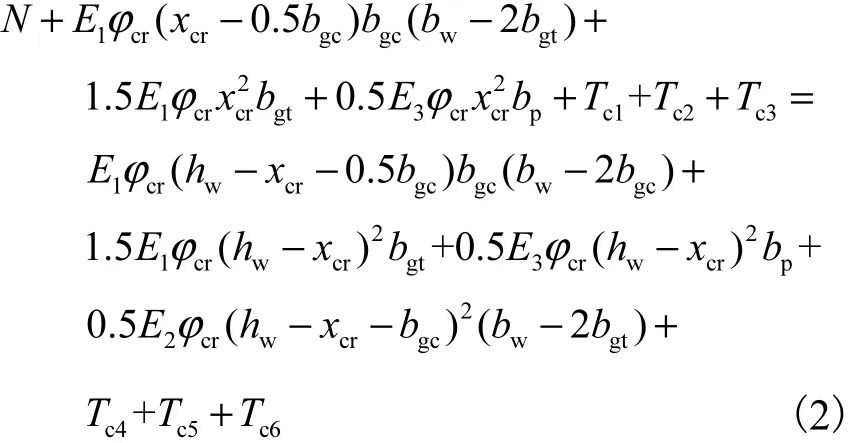
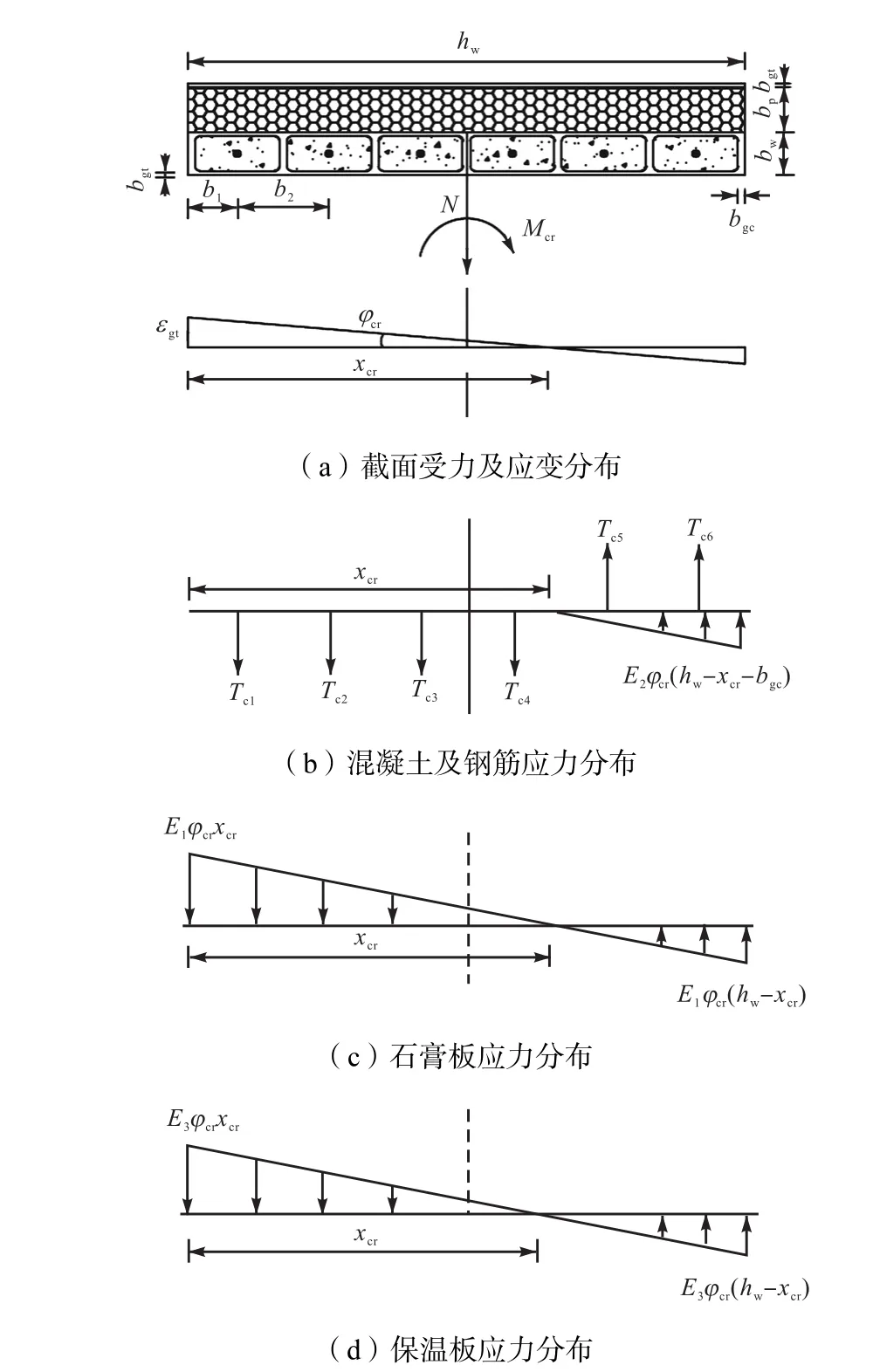
图5 开裂极限状态下的截面应力和应变图Fig.5 Stress and strain diagram of a cross-section in cracked limit state

由式(2)的计算结果可以求出xcr的大小，进而确定出构件截面开裂弯矩为

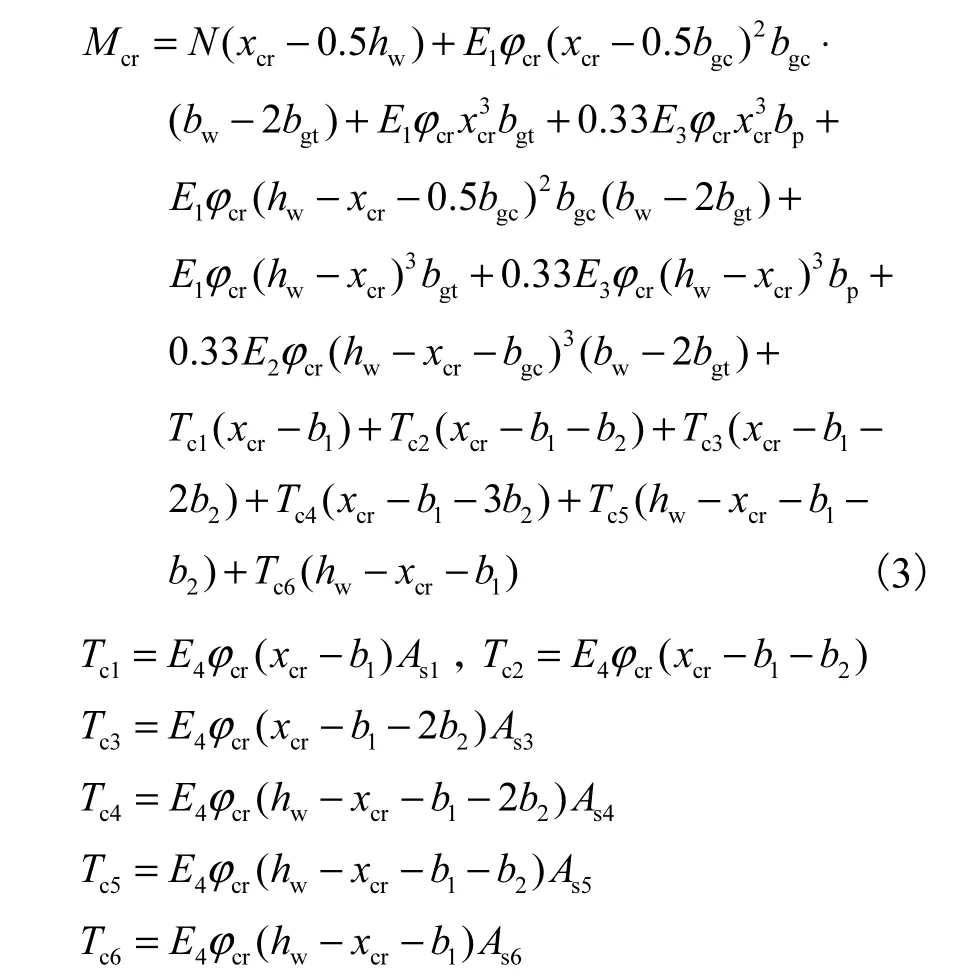
式中：Tc1～Tc6分别是开裂极限状态 1～6号混凝土芯柱中钢筋拉应力；E1、E2、E3、E4分别为纤维石膏、混凝土、保温板、钢筋的弹性模量，其中 E2=Eeq；N为竖向轴压力；xcr为截面开裂极限状态下的受拉区高度；ϕcr为截面的开裂曲率，；εcr为纤维石膏的开裂应变；As1～As6分别为 1～6号混凝土芯柱中钢筋的面积，将构件中的混凝土芯柱部分从左至右依次编号为 1～6．根据计算结果，保温板的内力较小，对开裂弯矩的贡献不大，在实际的计算应用中可以忽略式(2)和(3)中相应的计算项．

由式(2)、(3)可求出 xcr、ϕcr以及Mcr的值；然后求解开裂荷载以及开裂位移，即

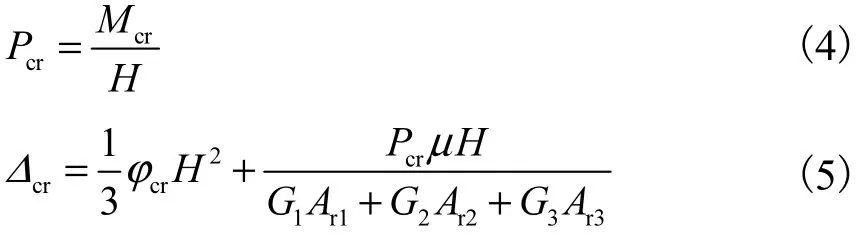
式中：H为构件的计算高度；Pcr为开裂荷载；为开裂位移；μ为剪应力不均匀系数，对矩形截面取μ= 1.2；G1、G2、G3分别为纤维石膏、混凝土、保温板的剪切模量，在没有试验值的情况下，可近似取Gi=0.4Ei(i＝1，2，3)；Ar1、Ar2、Ar3分别为纤维石膏、混凝土、保温板开裂极限状态下的有效剪切面积.

2) 开裂刚度

设Kcr表示开裂刚度，则有

2.2.2 屈服极限状态

1) 屈服荷载yP和屈服位移yΔ

构件在屈服前的加载过程中，边缘钢筋在达到屈服后，受压区的边缘混凝土仍处于弹性阶段．直到构件受压区边缘混凝土进入塑性阶段后，屈服前的力控制加载才结束．故本文采用文献[7]的建议，将受压区边缘混凝土进入塑性阶段所对应的临界状态定义为屈服状态，此时受压区边缘混凝土的应变为峰值应变的 70%,．

屈服极限状态下，构件受拉区外层纤维石膏板出现较多长裂缝，而保温板裂缝很少，故忽略受拉区纤维石膏板的作用，只考虑保温板和钢筋．

构件截面的应变和应力分布图如图6所示．

根据截面平衡条件，列出相应地平衡方程，同时考虑受拉区高度xy的取值范围，分情况讨论如下：

(1) 若 0 ＜ xy＜ b1− bgc，则有

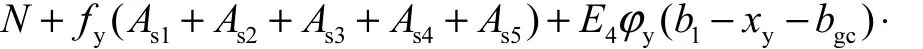
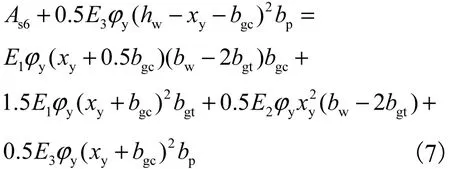
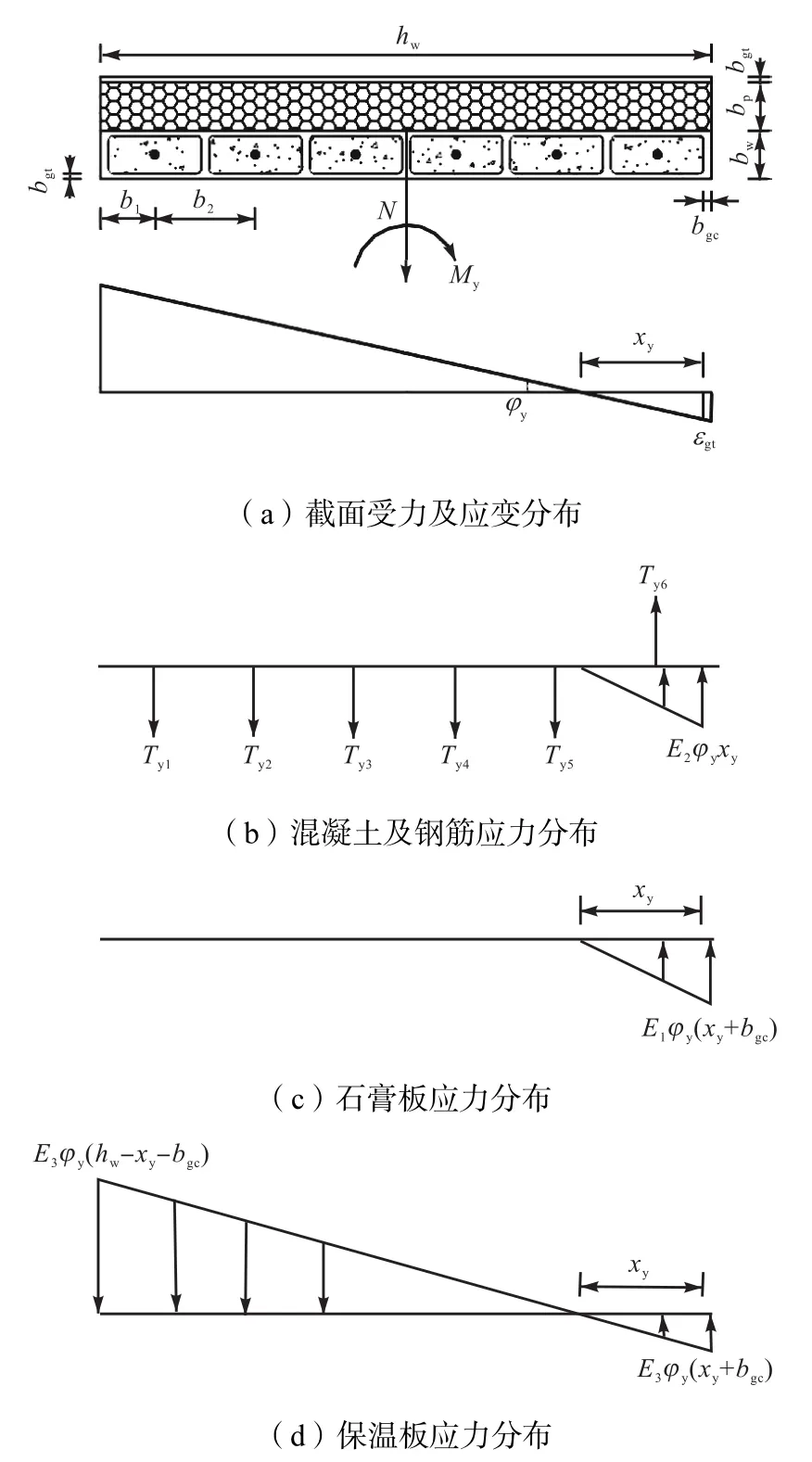
图6 屈服极限状态下的截面应力和应变图Fig.6 Stress and strain diagram of a cross-section in yield limit state

(2)若 b1− bgc＜ xy＜ b1+ b2− bgc，则有

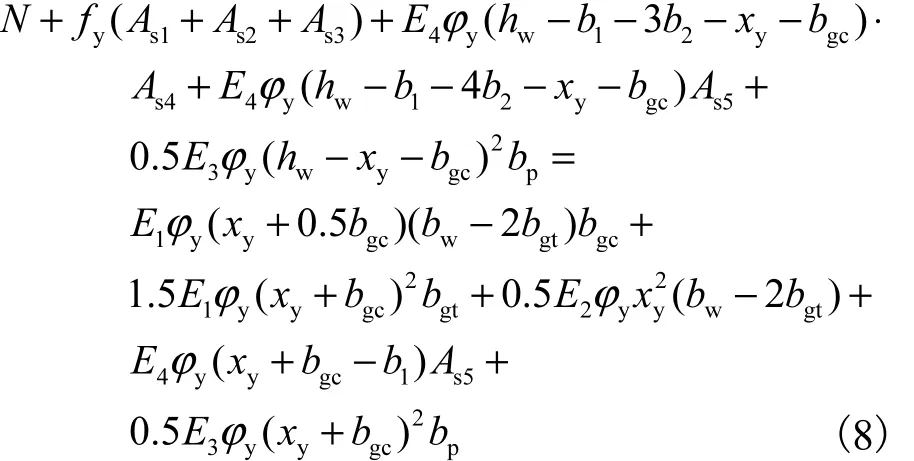
(3)若b1+b2− bgc＜ xy＜ hw− 0.5b2− bgc，则有

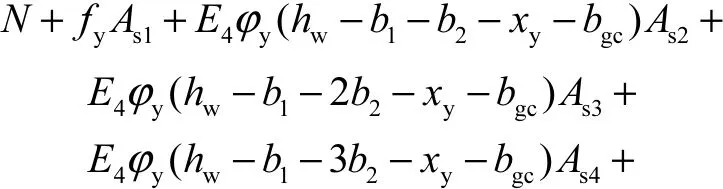
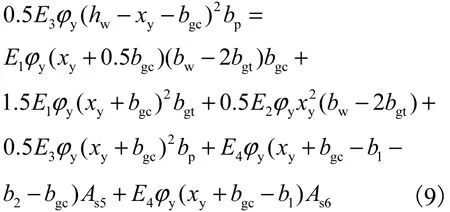
根据上述计算结果可知，在第2种情况下构件处于屈服极限状态，那么截面屈服弯矩可以计算如下：

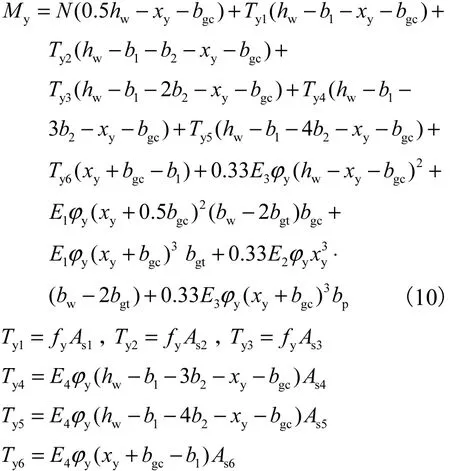
式中：Ty1～Ty6分别是屈服极限状态 1～6号钢筋的应力；xy为截面屈服极限状态下的受压区高度；ϕy为截面屈服曲率，为混凝土由弹性进入塑性的临界应变；fy为钢筋的屈服应力，根据钢筋拉伸试验得来．

根据计算结果，受拉区的钢筋承担主要拉力，受压区的混凝土承担主要压力，但是保温板和纤维石膏的作用不能忽略．

由式(7)、(8)、(9)以及(10)可求出xy、yϕ以及My的值，进一步可求解屈服荷载以及屈服位移

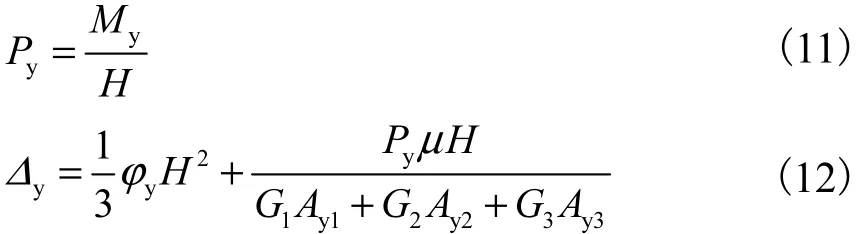
式中：Py表示屈服荷载；Δy表示屈服位移；Ay1、Ay2、Ay3分别为纤维石膏、混凝土、保温板在屈服极限状态下的有效剪切面积．

2) 屈服刚度

设Ky表示屈服刚度，则有

2.2.3 峰值极限状态

1) 峰值荷载Pm和峰值位移Δm

当构件达到屈服极限状态之后，受压区混凝土的压应变不断增加，直到混凝土芯柱边缘应变达到峰值压应变mε，构件进入峰值极限状态．

峰值极限状态下，构件受拉区纤维石膏板裂缝分布密集，表明石膏板退出了工作；受拉区的保温板裂缝也逐渐增多，出现了明显的长裂缝，故忽略保温板在受拉区的作用；受压区正面的纤维石膏板部分脱落，而外保温板面的纤维石膏板裂缝较少，故仅考虑外保温板面的纤维石膏板的受压作用．

构件截面的应力和应变分布如图7所示．

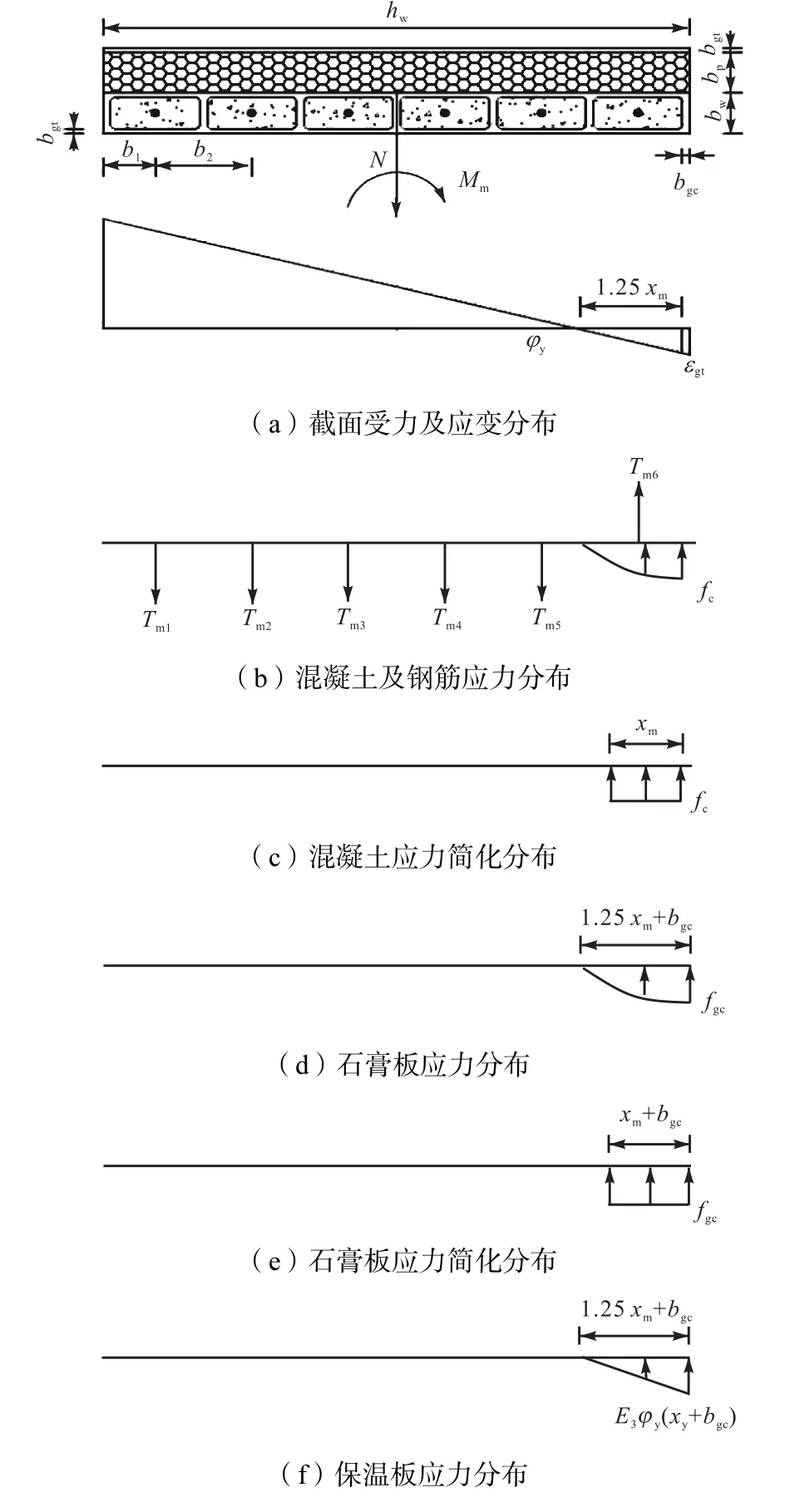
图7 峰值极限状态下的截面应力和应变图Fig.7 Stress and strain diagram of a cross-section in peak limit state

根据截面平衡条件，考虑构件的受压区高度xm的取值范围，分情况讨论如下：

(1) 若bgc＜ xm≤ b1−bgc，则有

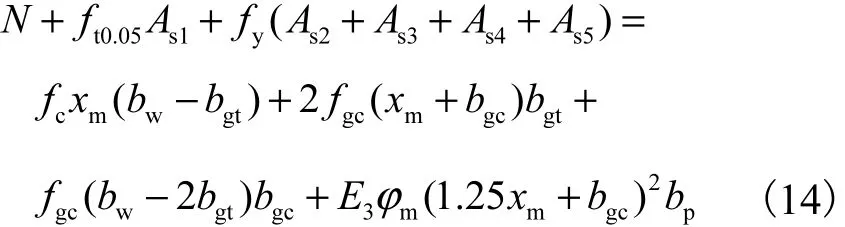
(2) 若b1−bgc＜ xm＜ b1+ b2−bgc，则有

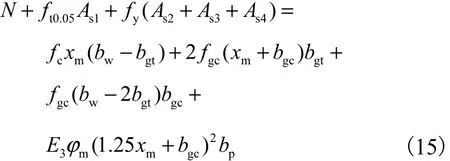
根据计算结果，第2种情况下构件处于峰值极限状态，相应地，截面峰值弯矩为

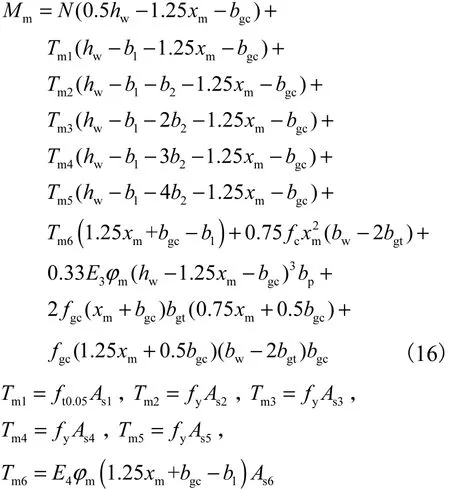
式中：Tm1～Tm6分别是峰值极限状态下 1～6号钢筋的应力；xm为截面峰值极限状态下的相对受压区高度；ϕm为截面峰值曲率，为非约束混凝土的峰值应力；fgc为纤维石膏的抗压强度；ft0.05为构件钢筋在应变为 0.05时对应的抗拉强度，通过计算以及试验钢筋应变观测结果[8]发现，在构件达到峰值极限状态时，受拉区边缘1号混凝土芯柱中的钢筋受拉应变可以达到 0.05左右，由于此时钢筋已经进入了强化阶段[9]，不能仅仅取为屈服强度，为保证计算的准确性，钢筋的抗拉强度取为应变为 0.05时对应的强度值．根据计算结果，钢筋和混凝土是主要受力部分，但纤维石膏板和保温板的作用仍不能忽略．

峰值荷载和峰值位移可分别计算如下：

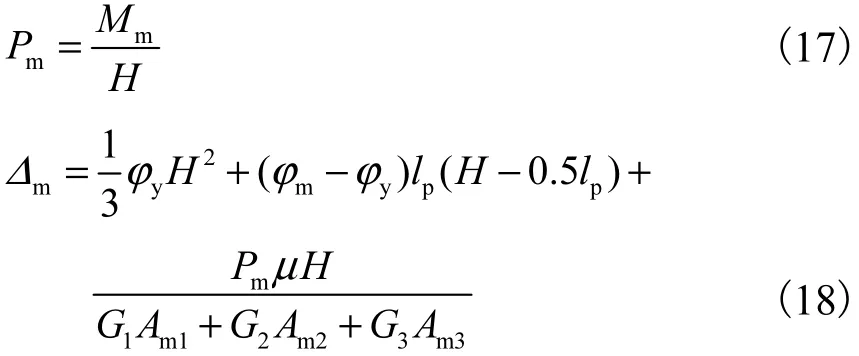
式中：lp表示构件塑性铰区长度，取 lp= 0.5hw；Am1、Am2、Am3分别为纤维石膏、混凝土、保温板峰值极限状态下的有效剪切面积．

2) 峰值刚度

设Km表示峰值刚度，则有

2.2.4 破坏极限状态

在峰值极限状态之后的加载过程中，构件的承载力并没有下降很多，而是位移量突然增大并导致破坏，有脆性破坏的趋势．这主要是由于构件的竖向钢筋配筋率较小，在峰值极限状态下，受拉区边缘混凝土芯柱内的钢筋进入了强化阶段，导致构件承载力下降不多．故假定构件在破坏极限状态下的承载力较峰值极限状态没有发生变化．

1) 破坏极限荷载和破坏极限位移

破坏极限荷载取为峰值荷载，即 Pu=Pm．

当构件受压区边缘混凝土达到极限应变εu时，构件的底部截面屈服曲率为

式中：uϕ为极限曲率；uε为混凝土的极限应变．

构件的破坏极限位移为

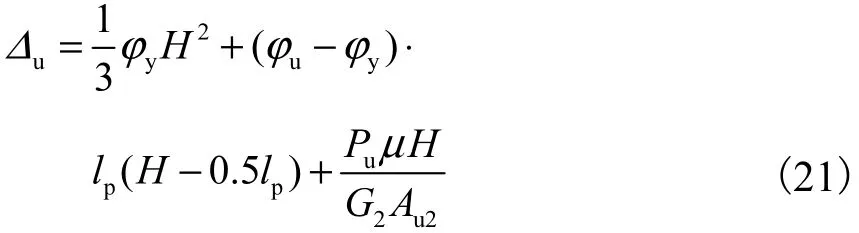
式中：uΔ表示构件的极限位移；Au2表示混凝土在构件破坏极限状态下的有效剪切面积．

2) 破坏极限刚度

根据假定可知，构件在破坏极限状态下的承载力没有发生变化，即构件的破坏极限刚度为0．

2.2.5 结果对比

通过上述计算，将得出的开裂点、屈服点、峰值点以及破坏极限点在坐标轴上连起来，就得到了新型混凝土石膏复合外墙板的骨架曲线，将计算曲线和试验曲线进行对比，如图8～图10所示．同时将各特征点的计算值和试验值进行对比，如表1所示．

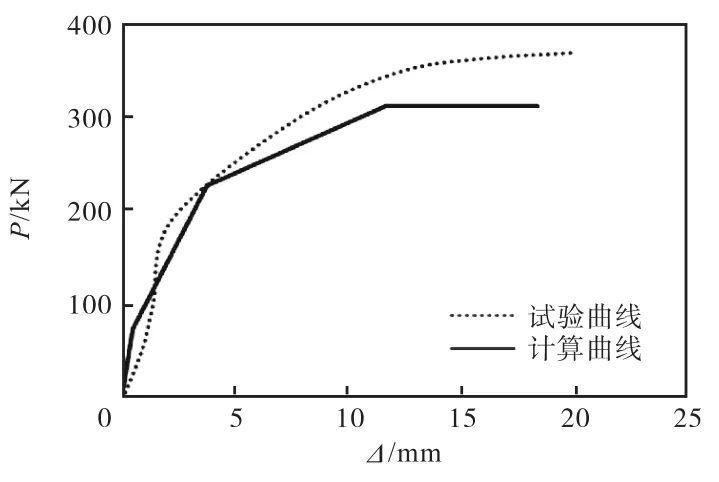
图8 计算骨架曲线和试验骨架曲线的对比(A-1试件)Fig.8 Comparison of calculated skeleton curves and experimental skeleton curves

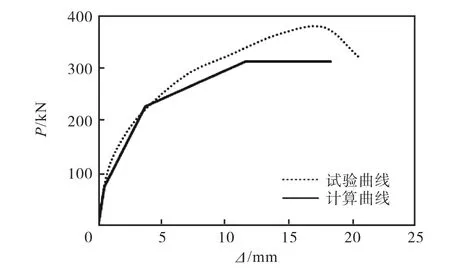
图9 计算骨架曲线和试验骨架曲线的对比(A-2试件)Fig.9 Comparison of calculated skeleton curves and experimental skeleton curves

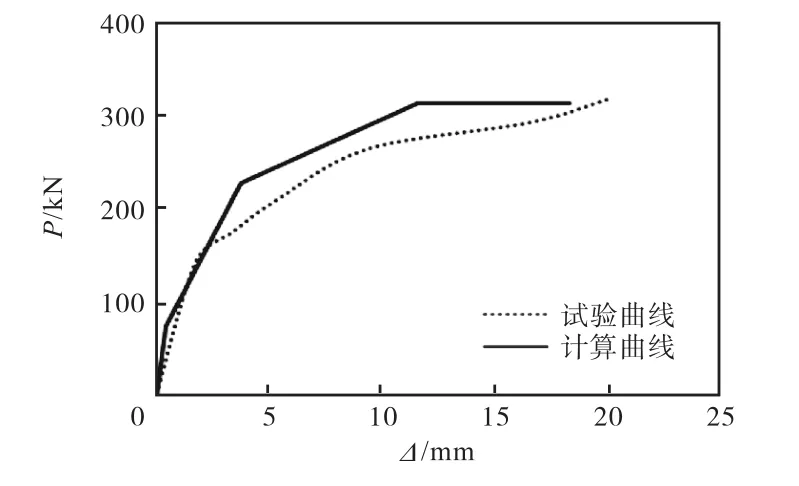
图10 计算骨架曲线和试验骨架曲线的对比(A-3试件)Fig.10 Comparison of calculated skeleton curves and experimental skeleton curves

表1 骨架曲线特征点的计算值与试验值Tab.1 Calculation values and experimental values of characteristic points of skeleton curve

3 滞回规则的建立

基于损伤的恢复力模型利用损伤指数来描述构件的整个破坏过程，能够很好地反映构件的滞回特征和各项力学性能的退化．西安建筑科技大学的王坤[10]、王斌等[11]基于双参数地震损伤模型提出了循环退化指数，并建立一种新的滞回规则，对具有梭形和弓形滞回环特征的滞回曲线进行了模拟[10-11]．

3.1 新型石膏混凝土复合外墙板的地震损伤模型

3.1.1 本文损伤模型的提出

本文选取最大变形处卸载刚度的退化和累积滞回耗能作为损伤参数，考虑极限耗能限值 Eu以及结构地震反应滞回环累积幅值对累积损伤的影响，同时对能量项引入修正系数γ，提出如下损伤模型：

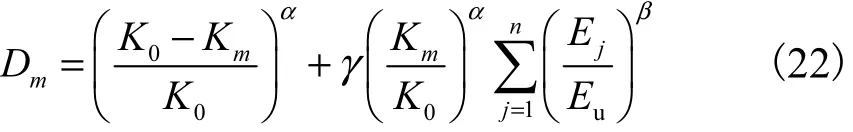
式中：n为第m级荷载下试件所经历加卸载的半循环次数；K0为构件的初始弹性刚度；Km为构件在第 m级荷载下的最大变形处的卸载刚度；Ej为第 j次半循环产生的耗能；Eu为试件的极限耗能能力，由骨架曲线与坐标轴围成的面积确定[12]；γ为修正系数；α、β为试验常数，其中β＞1，反映了加载幅值对滞回耗能的影响．

分析结果表明，新型石膏混凝土复合外墙板的骨架曲线计算值和试验值比较接近，且骨架曲线上各特征点的计算值与试验值的误差均在合理的范围内．这说明本文采用的计算方法可以较好描述新型石膏混凝土复合外墙板在地震作用下的开裂、屈服、峰值以及破坏极限状态，得到比较准确的骨架曲线特征点的值，进而近似得到新型石膏混凝土复合外墙板的骨架曲线．此外，由表 1可知，计算出的位移值普遍偏小，主要原因是在计算过程中忽略了剪切滑移的影响．

根据损伤的两种临界状态，并结合新型混凝土石膏板的低周反复荷载试验数据，对损伤模型进行非线性回归分析，得到损伤模型中的相关参数值为：α= 2，β=1.82，γ=4.7．

3.1.2 计算结果

分别利用式(22)、Park损伤模型[13]以及文献[14]中姚谦峰等提出的损伤模型计算新型石膏混凝土复合外墙板的损伤值．绘制新型石膏混凝土复合外墙板的损伤对比图，如图11所示．

由图11可知，与损伤试验值相比较，Park损伤模型的吻合度最小，其次是文献[14]中的损伤模型(姚模型)，本文提出的损伤模型与试验值最接近，这说明本文提出的损伤模型可以很好地反映新型石膏混凝土复合外墙板在地震作用下的损伤程度，为后面滞回曲线的模拟提供计算基础．

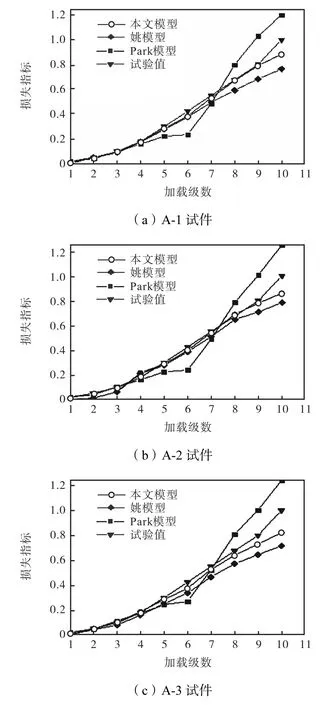
图11 损伤计算值与试验值的对比Fig.11 Comparison of calculated and experimental values of damage

3.2 滞回曲线的模拟

根据滞回环形式的不同，剪力墙构件的滞回曲线简化方法会有较大的不同．新型石膏混凝土复合外墙板的破坏形式属于剪切破坏，这也使得其屈服后的滞回环有明显的捏缩效应，呈反S形．

3.2.1 滞回环简化

在提出具体的滞回规则之前，需要先根据新型石膏混凝土复合外墙板的滞回曲线特征对滞回环进行简化．而屈服前和屈服后的试验滞回环差别较大，需要分别进行简化．

1) 构件在达到屈服状态前

构件在达到屈服状态之前的滞回环比较简单，没有捏缩现象．假设简化滞回环的加载段沿加载刚度与构件骨架曲线相交后，沿骨架曲线继续加载；当加载到该循环的控制荷载后，卸载段沿卸载刚度卸载至0，反向加卸载亦然．

2) 构件在达到屈服状态后

此时滞回环呈反 S形，捏缩现象明显．滞回环在开裂荷载附近有明显的拐点，如图12所示．不难发现，这个拐点的两边分别对应着构件的捏缩段和加载段．故假定构件捏缩段终点处的侧向荷载正好是开裂荷载．

为更好地描述滞回环的捏缩特征，本文定义捏缩段起点到终点连线的斜率为构件的捏缩刚度，即图13中的 AB段．由于捏缩现象是构件裂缝的开展和闭合所导致的刚度变化，即裂缝的不断开展会导致构件在捏缩起点处的刚度变化越来越显著，且捏缩起点处的荷载越来越接近 0．构件在整个反复加载过程中，随着损伤量的不断增加，构件的裂缝不断开展，从而捏缩刚度不断变小．基于这一事实，本文假定构件在捏缩起点处的刚度变化与损伤总量有关．

构件在开始卸载时，在位移不变的情况下，侧向荷载 P会突然下降，如图12所示．通过对试验滞回环曲线的分析发现，在构件循环加载的后期，侧向荷载P的下降值甚至可以达到0.18P，这意味着该下降段在恢复力模型中是不能忽略的．为更具体地描述滞回环上的这一下降段，本文用表示构件在第i次循环过程中正(反)向卸载顶点处的侧向荷载骤降值．

图12 试验滞回环Fig.12 Test hysteresis loop

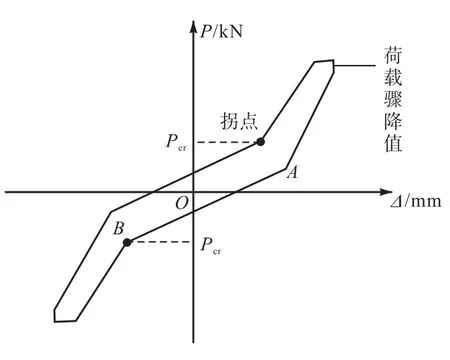
图13 屈服后滞回环的简化图Fig.13 Simplified diagram of hysteretic loop after yielding

3.2.2 退化分析

随着加卸载进程的进行，构件的各项力学性能不断退化，本文利用基于损伤的循环退化指数[11]来描述卸载刚度和再加载刚度的退化，如式(23)～(28)所示．

根据之前的假定，构件在捏缩起点处的刚度变化与损伤总量有关，将其关系表述为

构件在卸载顶点发生的荷载骤降现象，可以解释为构件在卸载顶点处的一部分可恢复变形转化为了不可恢复变形．设表示可恢复变形，表示不可恢复变形，那么在荷载骤降的整个过程中

这样构件在荷载下降后的变形就分成了3部分，分别是可恢复变形、转化之前的不可恢复变形、转化了的不可恢复变形增量．

在骤降过程结束后，侧向荷载的下降值可表示为

转化了的不可恢复变形增量又可以分为两部分，分别是构件加载至上一循环相同变形处，新增的可能转化为不可恢复变形的部分，用表示；继续加载的加载位移增量中可以转化为不可恢复变形的部分，用表示．那么

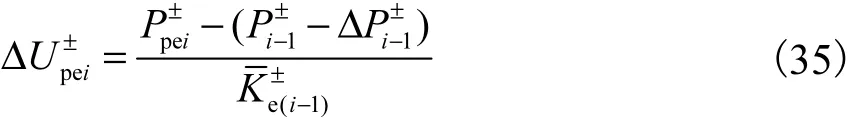
式中β为参数，β≥1．

根据式(32)～(36)，可以求出卸载顶点构件的侧向荷载下降值．

转化之前的不可恢复变形应为构件上一级荷载下同一方向的残余变形．

当荷载卸载至 0,kN时，构件的残余变形即为当前的不可恢复变形．转化了的不可恢复变形可以用同一加载方向上相邻的两次残余变形得到，即

那么构件在第i次循环加载过程中的残余变形为

3.2.3 滞回规则的提出

通过对滞回环的简化以及各项力学指标的退化分析，提出新型石膏混凝土复合外墙板的恢复力模型，如图14所示．其加载规则如下．

(1) 构件开裂前，加载和卸载路径沿构件的骨架曲线的弹性段进行．

(2) 构件开裂后，未达到屈服前，加载路径沿0123进行；卸载时，构件从点 3卸载至点 5，卸载刚度等于加载刚度；反向加载时，通过损伤公式(22)计算此时的损伤量，再加载刚度由式(24)和(26)计算得出，从点5沿再加载至刚度与构件的骨架曲线相交于点 7后，沿骨架曲线继续加载；卸载时，根据式(23)和(25)计算卸载刚度，然后继续卸载，再加载，路径同前所述．

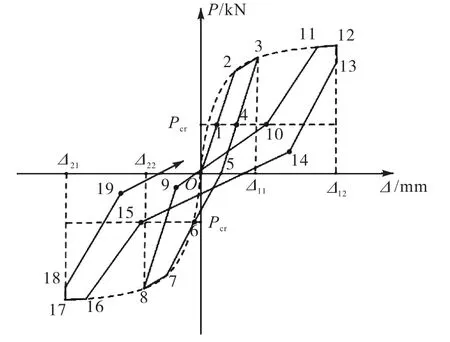
图14 新型石膏混凝土复合外墙板恢复力模型Fig.14 Restoring force model of new type gypsumconcrete composite exterior wallboard

(3) 构件屈服后，首先通过损伤公式(22)计算当前的损伤量，根据式(29)和(39)分别计算捏缩刚度和残余变形，然后确定捏缩起点 9，找到加载路径沿捏缩刚度加载至开裂荷载处的交点 10．根据式(24)和(26)计算再加载刚度，沿点 10、11和 12加载；卸载时，首先根据式(23)、(25)和(33)～(37)分别计算卸载刚度和侧向荷载骤降值，然后计算损伤量，进一步求解捏缩刚度和残余变形，确定捏缩起点 14；反向加载时，找到沿当前捏缩刚度加载至开裂荷载处的交点15，在根据式(23)和式(25)计算再加载刚度；反向卸载时，首先根据式(23)、(25)和(33)～(37)计算卸载刚度和侧向荷载骤降值，然后计算损伤量，求解出捏缩刚度和残余变形，确定捏缩起点 19，之后沿捏缩刚度继续卸载．再加载时的路径同前所述．

3.2.4 滞回曲线计算值与试验值的对比分析

根据上述滞回规则，可以得到新型石膏混凝土复合外墙板的计算滞回曲线，将其与试验滞回曲线放在同一张图里面进行对比，如图15所示．由图可知，计算曲线和试验曲线的吻合度较高．这说明本文提出的恢复力模型可以很好地模拟新型石膏混凝土复合外墙板的滞回特性和力学性能，可以为新型石膏混凝土结构的整体非线性分析提供基础资料和依据．此外，该恢复力模型的构建方法也可为其他类型的剪力墙构件提供思路，具有一定的借鉴意义．

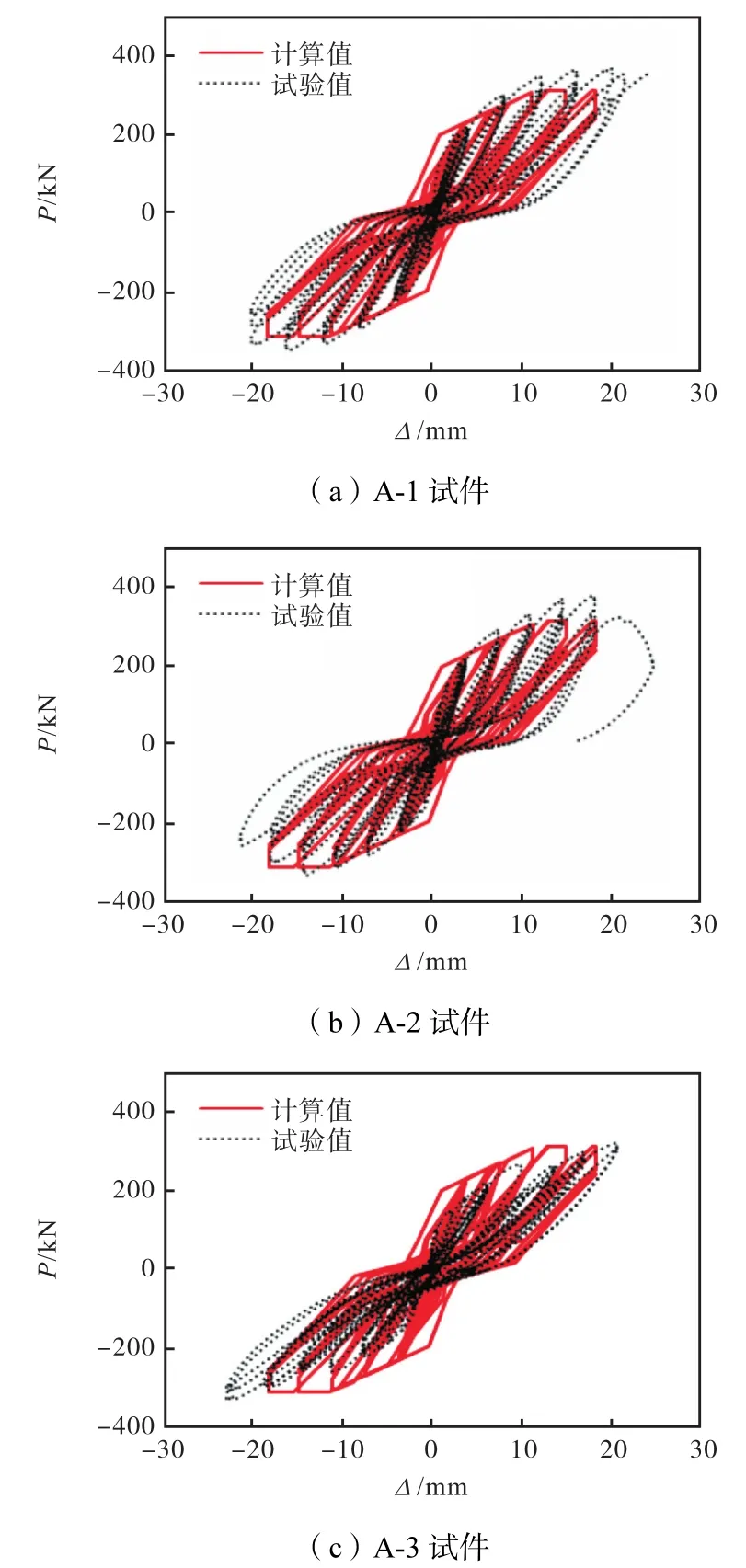
图15 计算滞回曲线与试验滞回曲线的对比Fig.15 Comparison of calculated hysteresis curve and experimental hysteresis curve

4 结 论

本文基于新型石膏混凝土复合外墙板的低周往复加载试验，进行了恢复力模型的相关研究，主要内容如下．

(1) 根据新型石膏混凝土复合外墙板的结构特点，推导了构件在不同极限状态下的顶点荷载-位移公式，求解出试件骨架曲线上的 4个极限特征点．通过与试验骨架曲线的对比分析发现，计算骨架曲线和试验骨架曲线吻合度较高，说明本文的计算方法是可行的．

(2) 通过对耗能项引入修正参数γ，提出了一种新的双参数地震损伤模型．通过与试验值的对比发现，本文提出的损伤模型可以较好地反映新型石膏混凝土复合外墙板在地震作用下的破坏损伤程度，为后面进行构件的恢复力模型研究提供了计算基础．

(3) 在提出的地震损伤模型的基础上，通过对试验滞回曲线的特征分析和滞回环的简化，提出了相应的滞回规则．将计算得出的计算滞回曲线与试验滞回曲线进行对比分析，发现二者吻合较好．这说明该恢复力模型可以很好地模拟新型混凝土石膏板在地震作用下的滞回特征，为石膏混凝土结构的整体非线性分析提供了依据．