水文频率分析的非参数统计计算方法

董 洁，谭秀翠，张庆华，刁艳芳，徐 妍

(山东农业大学水利土木工程学院，山东 泰安 271018)

0 引 言

水利建设规划设计时，要确定一个合理的设计标准或工程规模。一般采用水文频率分析方法计算设计值。目前主要有参数和非参数数理统计方法[1]。

用参数法推求设计值xp通常必须解决好两个基本问题：首先，必须确定水文变量的概率分布模型，即线型选择；其次，估计所选线型中的未知参数即参数估计[1]。由于水文现象影响因素的复杂性，有些水文学者从统计理论上分析论证水文变量服从的分布，提出了很多线型供选择，例如P-Ⅲ型分布、对数正态分布和K-M分布等线型，但是水文变量的真实分布是很难确切表达的。在实际水文工作中，常根据实测经验点据和频率曲线拟合的好坏选择线型，由于实际应用中评判拟合优劣的标准各异，所得结论往往相差较大[2]。根据我国水文特点，一般水文变量采用P-Ⅲ型分布。每一种概率分布中都包含若干参数，选定线型后还必须确定其中的参数才能进行频率计算。但是这些参数是无法根据水文现象的物理机制确定的，必须利用实测资料加以估计。因此，国内外水文学者研究了很多符合水文特点的参数估计方法，主要有适线法，权函数法和概率权重矩法等。由于水文系列长度短，且所需推求的是稀遇的设计值等原因，参数统计估计方法并不理想。

非参数统计中的概率密度估计是指在给定实测样本后，对其总体概率密度的估计。非参数概率密度估计始于直方图法，后来发展为最近邻法、核估计法等，其中理论发展最完善的是概率密度核估计法[3]。

本文把非参数回归理论应用于水文频率计算中，建立了水文频率分析的非参数回归变换模型，通过变换把样本变换成“最佳样本”，“最佳样本”对应的“最佳函数”具有较高的估计精度。

1 非参数回归变换理论

设(X1,Y1),…,(Xn,Yn)是R1×1维随机变量，满足模型：

Yi=m(Xi)+εi,i=1,2,…,n

(1)

式中：εi是均值为零的独立随机变量。

回归的目的就是根据样本(Xi,Yi)估计Y关于X的条件概率密度的均值：

m(x)=E(Y|X=x)

(2)

Watston给出了条件均值的核估计：

(3)

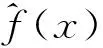
由于核回归是两个量的比，直接求核回归的偏差比较困难，可以分别考虑上式分子分母的偏差。

(4)

其中：[m(·)f(·)]″(x)=m″(x)f(x)+2m′(x)f′(x)+m(x)f″(x)。

将原样本Xi变换为均匀分布的新样本Ui，目的是对Yi进行加权平均时，权的大小只与样本的邻近次序有关，与距离无关，这体现了各样本互相独立的原则。只要知道Xi的分布函数F(x)，就能进行变换Ui=F(Xi)。

这里假定Xi已经变换成均匀分布的样本Ui，现在只讨论因变量样本Yi的变换。设Vi是均值为1的随机样本，可以进行如下“加法”迭代。

加法迭代的基本原理是将回归曲线分解成两条曲线的和，第一条曲线接近回归曲线，第二条曲线接近常数0。迭代方法如下：

(5)

式中：l是迭代次数。

2 水文频率分析非参数回归变换模型的建立

2.1 分布函数的非参数变换估计

分布函数估计与密度估计一样有许多重要的作用。当样本数量足够大时，经验分布函数可以近似逼近总体的分布函数，但是如果样本数量较少，表现为阶梯函数，使得经验分布函数估计受到限制。如果想由密度函数估计得到分布函数估计，密度函数估计应是无偏的，方差大点不要紧，因为积分时会消除方差的影响。若要从分布函数得到密度函数估计，分布函数应连续光滑，有点偏差不要紧，数值微分是用邻近几个点估计一个点的微分值，对非光滑点(方差大的点)很敏感。因此，一个合理的想法是利用经验分布的无偏性加以平滑就得到偏差和方差都较小的估计。这种方法是非参数回归的一个特例，不同之处在于因变量不是事先得到的样本，而是分布函数的无偏估点计。因此分布函数估计的第一步，是构造无偏估计点作为回归的因变量。下面采用经验分布函数作为分布函数的无偏估计。

2.2 样本经验分布函数

设x1,x2,…,xn,是随机样本，有分布函数F(x)，考虑水文的特点，取经验分布函数是：

(6)

式中：n为样本的个数；m为样本x大于等于某个给定值的个数。

对上式的经验分布函数定义：除x为样本点外的Fn(x)仍和式(6)一样，而x=xi处的分布函数估计值为：

(7)

x1≥x2≥…≥xn

其中，α是[0，1]区间的常数，通常取α=1。

由式(6)和式(7)定义的函数称为样本经验分布函数。

提出样本经验分布函数的理由如下：先考虑只有一个样本即n=1，样本出现对应一次贝努利试验，出现的概率是α/2，也就是样本位于α/2分位点。若样本取自中心较高且具有对称密度函数的母体，α/2=0.5意味着单个样本位于分布的中点，对应最大的概率密度。此时的经验分布函数符合最大似然准则。对于n个样本，由于各样本是独立同分布，样本分布函数值将分布函数等分。样本应位于等分后的每小块中的α/2分位点上，即各样本等间隔地位于(i-1-α)/(n+1)分位点上。这个想法与离散分布中的古典概率论一致。

显然，样本经验分布函数的性质与经验分布函数一致，由式(6)知，样本经验分布函数是小于等于样本值的样本数与样本总数加一之比，因此nF(xi)是二项分布随机变量，则有样本经验分布函数的均值和方差为：

E[Fn(xi)]=F(xi)

varFn(xi)=F(xi)[1-F(xi)]/n

(8)

所以样本经验分布函数是无偏估计，这为回归提供了好的先决条件。在样本经验分布的基础上回归，可使分布函数的方差减小。另外，以样本经验分布函数为固定点进行内插，也可得到比较光滑连续的曲线，但是这样得到的曲线保留了样本经验分布函数的方差，这个方差的最明显的证明是对内插得到的曲线进行微分，得到的密度函数估计存在许多毛刺和突起，微分对方差的敏感是检验方差存在的直观方法。

2.3 样本经验分布函数的变换回归

由前面定义知，样本经验分布函数是：

(9)

i=1,2,…,n

记yi=Fn(xi) ，则(xi,yi)构成R1×1维随机变量，可以进行非参数回归计算。但这里的yi不是通常回归中事先给出的样本，是分布函数在xi点的无偏估计。将原样本(xi,yi)变成新样本(ui,vi)，其中vi是均值为1的随机变量，ui是均匀分布随机变量。

由于样本Xi不是等间隔的固定点，变换回归包含自变量X和因变量Y的两步变换，将原样本(xi,yi)变成新样本(ui,vi)。在分布函数估计中，这两步变换可以一起完成，因为Yi和Xi有一定的关系。

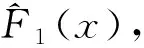
(10)

此时的Yi相当于U1,i近似于45°斜线，则：

V1,i=Yi-U1,i+1

(11)

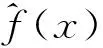
变换回归的偏差很小，基本上是无偏回归，因样本经验分布函数也是无偏估计，所以最后得到的分布函数估计是无偏估计。

3 蒙特卡罗统计试验分析

蒙特卡罗统计试验分析[6,7]可以很好的说明模型的稳健性问题。假设水文变量分别来自P-Ⅲ型分布和对数正态分布总体，用参数统计的适线法和非参数核回归变换法比较分析模型对总体和样本数量的稳健性。

3.1 试验方案

为了考察模型对样本数量和不同设计频率的稳健性，分别选取了样本容量n1=40；n2=50；n3=60；设计频率p1=0.01,p2=0.001。

3.2 计算方案

用蒙特卡罗方法生成P-Ⅲ型分布和对数正态分布LN样本，为了考察模型对样本总体和计算方法的稳健性，设计了108种方案。分别采用非参数的核回归变换法DRM；参数统计的适线法CFM估计设计值。计算结果见表1和2。(只列出样本容量为n=60的结果)

3.3 评价指标

(1)均方误差σ和相对均方误差δ：

(2)绝对误差θ和相对误差ϑ。

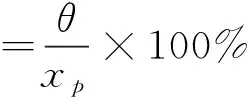
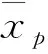
3.4 统计试验结果

统计试验结果见表1、表2。

3.5 估计方法的比较分析

表1和表2分别用4个评价指标计算了P-Ⅲ型分布和对数正态分布(LN)，拟合理论总体是P-Ⅲ型分布和对数正态分布(LN)的稳健性，分析结果如下：

(1)总体是P-Ⅲ型分布。当用P-Ⅲ型分布曲线拟合P-Ⅲ型分布总体时，ϑxp1≤1%；ϑxp2≤1%δxp1≤15%δxp2≤20%。

当用对数正态分布(LN)拟合P-Ⅲ型分布，总体适线的稳定性较差，ϑxp1≥120；ϑxp2≥20%δxp1≥25%δxp2≥25%。

当用非参数的密度变换法DEM估计设计值，百年一遇和千年一遇的设计值相对误差一般介于以上两种情况之间，ϑxp1≤15%；ϑxp2≤15%δxp1≤15%δxp2≤20%。

(2)总体是对数正态分布(LN)。当用对数正态分布(LN)拟合对数正态分布总体，ϑxp1≤8%；ϑxp2≤8%δxp1≤15%δxp2≤20%。

当用P-Ⅲ型分布拟合对数正态分布LN总体适线的稳定性较差，一般求出的设计值偏小，很不安全。δxp1≥15%δxp2≥20%。

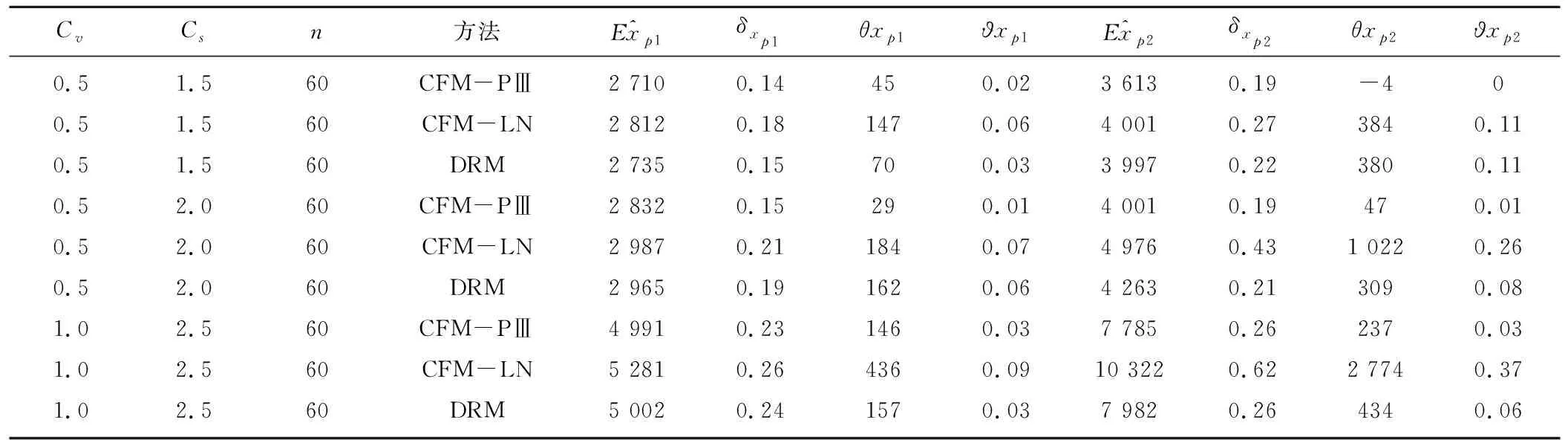
表1 P-Ⅲ型分布理论总体计算成果表(p1=0.01,EX=1 000,p2=0.001)Tab.1 Calculation result of P-Ⅲ theory distribution (p1=0.01, EX=1 000, p2=0.001)

注：各组真值xp如下：Cv=0.5，Cs=1.5时，xp1=2 665,xp2=3 617；Cv=0.5,Cs=2.0时，xp1=2 803,xp2=3 954；Cv=1，Cs=2.5时，xp1=4 875，xp2=7 548。

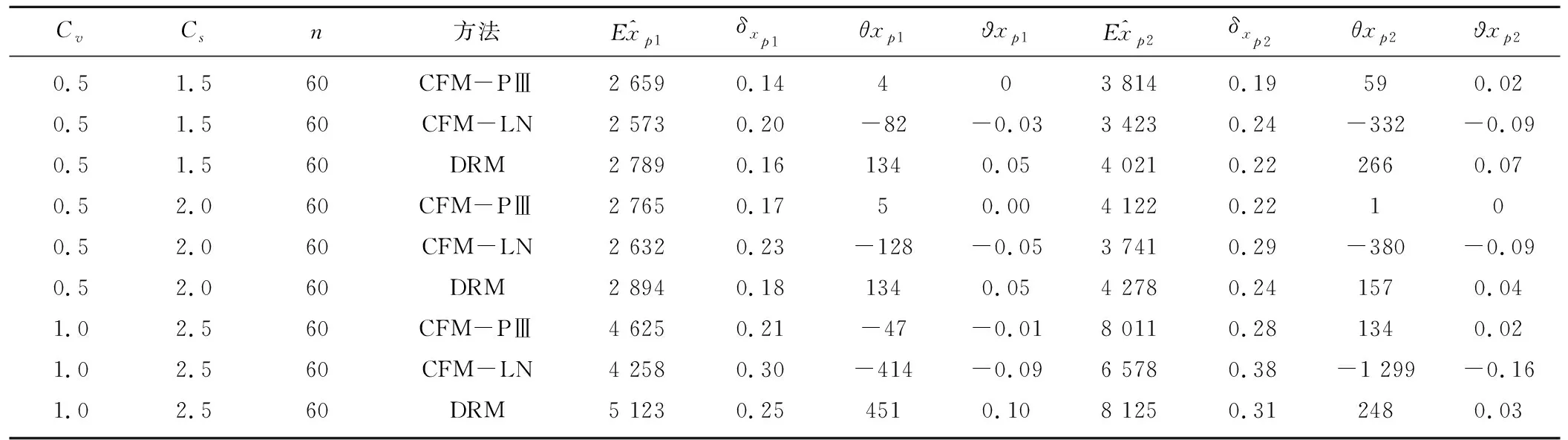
表2 对数正态分布理论总体计算成果表(p1=0.01,EX=1 000,p2=0.001)Tab.2 Calculation result of Logarithmic normal theory distribution (p1=0.01, EX=1 000, p2=0.001)

注：各组真值xp如下：Cv=0.5，Cs=1.5时，xp1=2 665，xp2=3 755；Cv=0.5，Cs=2.0时，xp1=2 760，xp2=4 120；Cv=1，Cs=2.5时，xp1=4 672，xp2=7 877。

非参数的回归变换法DEM估计设计值，百年一遇和千年一遇的设计值相对误差一般介于以上两种情况之间，ϑxp1≤15%；ϑxp2≤15%δxp1≤15%δxp2≤20%。

当样本容量由40、50增加到60，相对误差和相对均方误差减小，说明样本容量增加，稳定性增加。

4 应用实例研究

为了更好地检验该模型的适用性,以下对具有代表性的小浪底站77 a；宜昌站132 a；岗南站57 a；平山站30 a和黄壁庄站56 a的年最大洪峰流量系列，用P-Ⅲ适线法和变换回归模型进行了频率分析计算,各站年最大洪峰流量系列资料表详见文献[8]，计算成果见表3。通过以上计算可以看出，用非参数回归变换模型计算出的设计值比适线法计算的值普遍偏大，频率P大于百年以上的设计值较参数适线法计算的设计值大3%～7%；频率P小于百年以下的设计值较参数适线法计算的设计值大2%～3%。

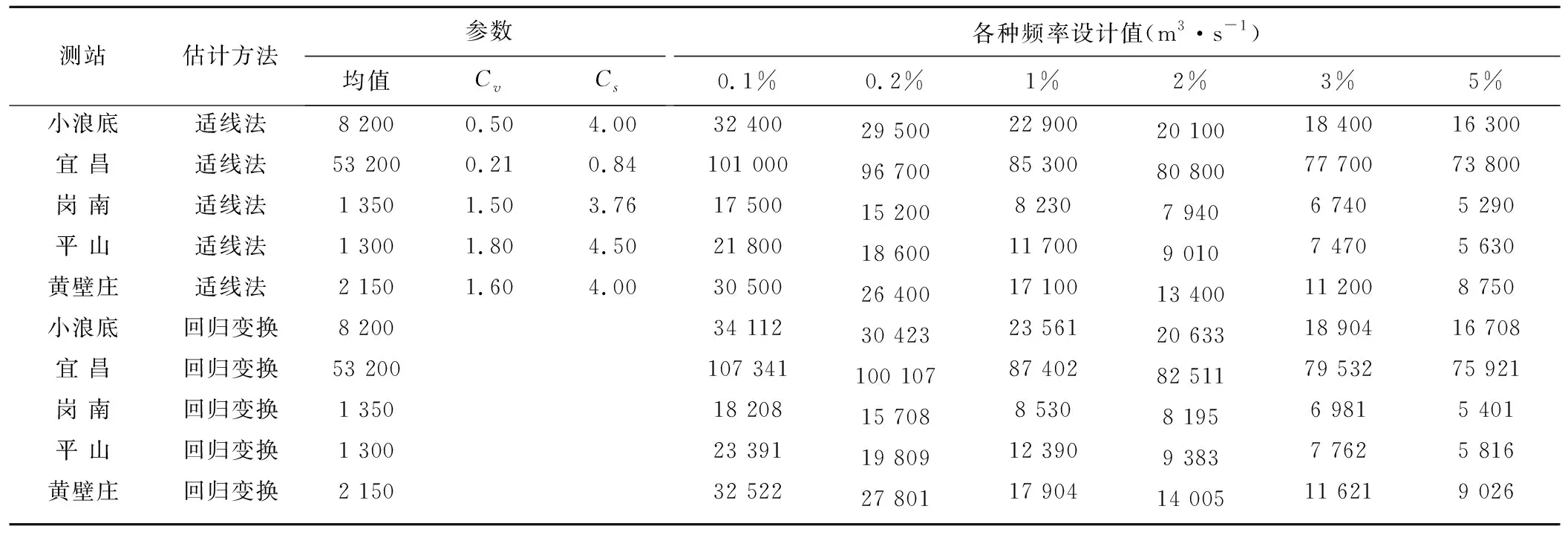
表3 小浪底站、平山等站年最大洪峰流量频率分析结果Tab.3 Flood frequency analysis of the XIAOLANGDI station and PINGSHAN station

5 结 语

(1)我国水文频率计算一般采用参数统计的“适线法”。需要事先假定水文变量服从某种线型分布，如果假设线型和实际分布不符就会影响计算结果。非参数统计方法不需要假定线型，但是理论上要求适用于大样本。本文建立的非参数回归变换方法通过对小样本进行变换，不仅拓展了非参数统计的应用，还提高了小样本的估计精度。

(2)用蒙特卡罗统计试验方法考察模型的稳健性问题。通过对水文计算中常用的P-Ⅲ型和对数正态分布两个总体，用参数统计的“适线法”和非参数统计的“变换回归”两种估计方法比较分析了三组参数、三组样本。结果表明，模型是稳健的，方法是合理的。

(3)以我国几个有代表性的测站的年最大洪峰流量为例，比较研究变换回归模型和参数适线法在水文频率分析计算中的结果特征，通过计算得到用非参数方法计算的水文频率结果较适线法偏大，多种计算结果可以互相参考，为水利工程规划提供了一种有效方法。