气介式自校正声波水位计精度研究

郑贵林，董启鹏

(武汉大学动力与机械学院自动化系，武汉 430072)

0 引 言

在电子技术被引入水位计的研制之前，水位计大多是通过测量与水相关的参数来间接转化为水位参数，以达到水位测量的目的，如浮子式和压阻式水位计[1]。后来，随着传感器技术和嵌入式技术的发展，出现了更多的水位测量方法，比如利用雷达、激光、超声波等技术的水位测量传感器，具有智能控制功能，可实现非接触式测量，且精度高、稳定性好[2]。

牛睿平等在文献[3]中提出了一种新型国产雷达水位计的设计，盖志刚等在文献[4]中提出了一种新型激光智能水位测量系统的研制，蓝标在文献[5]中提出了高精度气介式超声波水位计的设计，汤祥林等在文献[6]中提到的低功耗、高精度超声波水位计的研制。

以上文献中研究的新型水位计，量程都相对较小，对环境要求较高。而对于库容较小的水库而言，采用雷达水位计和激光水位计成本较高，采用超声波水位计受环境影响较大。因此，设计一种量程相对较大，成本较低，对环境敏感度不高，且易于安装的水位计，可以很好地解决以上问题。针对此需求，本文设计了一种气介式自标定声波水位计，创新地采用了AD采集与sinc内插算法相结合的峰值检测方法，避免了传统的由于采用阈值比较法而对回波进行复杂硬件电路的处理，并进行了长期实验。

1 声波水位计原理

本文设计的气介式自标定声波水位计采用空气声学回声测距原理，借鉴的是超声波测距中最常用的脉冲回波法，结合可闻声波换能器的声学特性，最终设计出了该传感器测量系统。

该系统测量原理即是控制声波换能器即扬声器发射声波信号，声波在空气中传播时，遇到不同体积或材质的物体，将会有不同形式、不同幅值的回波[7]。由于扬声器不同于超声波换能器能在脉冲的激励下，产生单一频率的超声波信号，扬声器在输入脉冲信号时，只会产生其频率响应范围内的信号，所以本设计中输入信号采用单一频率的正弦信号。为了避免环境中温度、湿度、大气压等环境因素的影响，本设计中采用声学自校正的方法。

图1 测量示意图Fig.1 Instrumentation plan

该水位计主要由声波探头、波导管及测控单元组成，测量示意图见图1。图1中L1表示的是声波探头安装位置至第一拐点的长度，L2、L3和L4为按现场大坝铺设的长度，L5为最后一个拐点至水面的长度，α和β为铺在斜坡上的波导管的角度。l为两个标定点的距离，L为从声波探头至测量水面的总长度。

声波在空气中的传播速度为v，如果测得声波从开始发射到接收到反射回波的时间t，就能计算出从声波探头到反射面的距离S，即：

S=vt/2

(1)

测量时，由声波探头发射的声波信号沿波导管到达水界面产生反射回波，然后返回至声波探头而被接收，所以只需准确测出声波信号从开始发射到接收到回波信号的时间t1及传播的声速c1，便可计算出声波探头反射面至水面的距离。即：

L=c1t1/2

(2)

声波在波导管中传播速度的影响因素有温度、湿度、大气压等，所以要想利用式(2)准确测得声波探头反射面距水面的距离，那么就要解决上述影响因素的干扰，因此在本设计中采用了自校正技术对声速进行补偿。其方法是在距声波探头2 m处和3 m处分别放置一块挡板，如图1中2 m和3 m标定处，声波在标定处会产生回波，由于2 m到3 m的距离是已知的，所以这段时间可以作为声波此时在管道中传播1 m的基准值，记这个时间基准值为t2，此时，如果声波传播的声速为c2，即有：

l=c2t2/2

(3)

将声波在这段时间基准值内传播的距离与声波传播到水面反射面的距离做比则有：

(4)

由上式可知，声程L是传播速度c1、c2与传播时间t1、t2和时间基准值内传播距离l的函数。若近似认为在波导管中不存在温度梯度时，那么可得c1=c2，则式(4)可化简为：

(5)

故在忽略波导管内温度梯度的情况下，只需测出t1、t2，即可测出声波探头到水面的距离。

计算出声波探头至水面距离后，根据L1、L2、L3、L4和L5来判断水位处于哪一段波导管中。假设声波探头安装位置高程为H1，测出声波探头至水面距离L，且判断出水面在L5段，那么水位H可由下面公式得出：

H=H1-L1-L3sinα-(L-L1-L2-L3-L4) sinβ

(6)

若判断出水位处于L3段，那么水位H由下面公式得出：

H=H1-L1-(L-L1-L2) sinα

(7)

2 系统设计与实现

系统具体实现如下：由ST公司基于ARM Cortex-M3内核的STM32F103微控制器控制信号产生电路产生单一频率的正弦波信号，经发射信号处理电路处理后，由信号功放电路放大送入扬声器驱动发声。由麦克接收回波信号，并进行阻抗匹配，然后经过Maxim公司的麦克专用放大器进行前置放大，这时的信号还不满足信号处理的要求，所以还要进行信号调理，最终经过信号调理后的波形由STM32进行AD采集，并采用sinc内插算法高度还原波形，以更精确地得出实时水位。实时波形及相关数据通过RS485总线或GPRS模块上传至云端服务器，并通过上位机显示和查看。系统实现框图如图2所示。

图2 系统实现框图Fig.2 System structure

该声波探头实物如图3所示，安装时开口处朝下接波导管，上端封闭，引出电源线与太阳能板相连。

图3 声波探头实物 Fig.3 Sonic probe

3 精度影响因素

在本设计中，主要有三个因素会对测量精度造成影响，分别是声源的选择、功放电路与扬声器是否匹配及回波时间捕捉的精确性。

3.1 声源的影响

由于可闻声波采用扬声器作为换能器，在激励信号即声源的使用上不同于超声波换能器，超声波换能器在脉冲激励信号的驱动下，可发射其固有频率的超声波。但扬声器的频响范围比较有限，当输入方波信号时，扬声器并不能复现方波信号[8]。基于此，在本研究中，将声源信号确定为单一频率的正弦信号，频率在1～20 kHz，正弦波产生方式采用直接数字频率合成技术(DDS)，使用ADI公司的可编程波形发生器AD9833。

3.2 功放电路与扬声器匹配的影响

扬声器是瞬态表现的最大瓶颈，要求瞬态表现好，则扬声器振膜需要做到快速到位的运动，这对扬声器的控制力提出了非常苛刻的要求[9]。而要响应高于2 kHz频率的输入信号，需要用高频喇叭继续试验。

另外，“瞬态表现好”需要大功率功放和电源支持的，信号迅速提升的瞬间，峰值功率可能会是平均功率的数倍甚至十余倍，基于这个原因，选取了2 W的高频喇叭实验，并更换功率10 W的功放，以使扬声器可以瞬间响应输入频率。

3.3 捕捉回波时间准确性的影响

传统的回波信号检测方法有幅值检测法、相位检测法和渡越时间法，而采用最多的渡越时间法。渡越时间法又包括阈值检测法、峰值时间检测法[10]等。本设计中采用峰值时间检测法，但不采用传统的硬件方法，而是将接收到的声波信号的模拟量通过STM32内置AD转换成数字量，利用sinc内插算法对采样点重构波形，从而更精确地得到峰值点，就可以计算出回波时刻。

信号插值是增加抽样率以增加数据的过程，一般的信号插值基本结构[11]如图4所示。

图4 信号插值基本结构Fig.4 The structure of Signal interpolation

假设采样序列为x(n),原采样率f，在x(n)的每两个采样点之间等间隔插入(L-1)个零点,得到一个新的采样序列v(n),即：

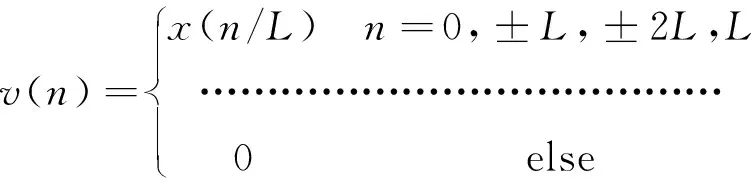
插零后信号的频谱：

于是可得：

V(ejw)=X(ejwL)

即插零后信号频谱V(jw)(-π/L～π/L) 内等于X(ejw)，相当于将X(ejw)作了周期压缩。 然后再通过一个低通滤波器：

就可以将高频信号滤掉从而得到插值后的信号y(n)。信号插值过程示意图如图5所示，图5(a)为原信号x(n)及其频谱X(ejw)，图5(b)为插入零值点后的信号v(n)及其频谱V(ejw),图5(c)为插值后信号y(n)及其频谱Y(ejw)：

图5 信号插值过程Fig.5 The process of signal interpolation

由参考文献[12]，利用sinc函数内插的公式为：

(8)

式中Δ=1/f。

4 实验分析

基于上述影响因素搭建了实验，声源信号采用5 kHz单一正弦波，扬声器功率2 W，采用驻极体话筒来接收回波，并进行信号调理。经STM32的AD采样后，将采样数据发送到上位机进行显示。从开始发送声波到接收回波时间内采集的离散点如图6所示，横坐标为采样周期，纵坐标为AD采集值，AD为12位 1 MHz采样率。图中相邻离散点通过线段相连从而绘制出整体波形。由于AD采集只能采集到正值，所以波形只有正弦正半波。图6中，第一个正弦半波为2 m处回波，第二个正弦半波为3 m处回波，幅值最高处为目标处回波。

图6 AD采集波形Fig.6 AD waveform acquisition

将最高处正弦半波放大，经多次实验观察放大后的波形，采集的最高点并不是峰值点，要想精确地捕捉到三个正弦半波的峰值点，就要用sinc插值公式(8)来对波形进行处理。放大后的原峰值附近波形及利用sinc插值算法得出的波形如图7所示，横坐标为时间t，纵坐标为AD采集值。这里只把原波形的包括最高点在内的16个点画出，其中最高点附近6个点的坐标分别为：

(6,3 836)(7,3 926)(8,3 985)(9,3 972)(10,3 912)(11,3 813)

在每两个采样点之间插入了4个零值，即采样率提高了5倍，插值后的波形最高点附近6个点的坐标分别为：

(7.8,3 969)(8,3 985)(8.2,3 987)(8.4,3 990)

(8.6,3 986)(8.8,3 980)

图7 原波形与正弦插值后波形 Fig.7 The waveform of before and after processing

于是可以根据插值后新的序列来比较出最高点作为新的峰值点，同样的，对2 m和3 m处回波作sinc插值处理。然后利用公式(5)计算声程，再用公式(6)或(7)计算出水位。相比于根据原波形计算出的峰值时刻点，在进行声波测水位实验时，实测结果与测量结果的偏差较小。表1实验数据为部分实验水位、实测水位及误差，表中实验水位1为根据原波形计算出的实验水位，误差1为实验水位1与实际水位相比较的误差，实验水位2为根据正弦插值算法处理后的波形计算出的实验水位，误差2为实验水位2与实际水位相比较的误差。

表1数据表明随着实际水位的增高，利用原波形的AD采样数据进行计算的水位结果与实际水位的偏差会稍微变大，但是利用经过正弦插值算法处理的波形，进行计算，可以保证误差在1 cm之内。

此外，在实验室搭建了模拟环境，改变该水位计所处环境温度和环境湿度，检测温湿度对于测量精度的影响。实验结果分别如表2、表3所示。

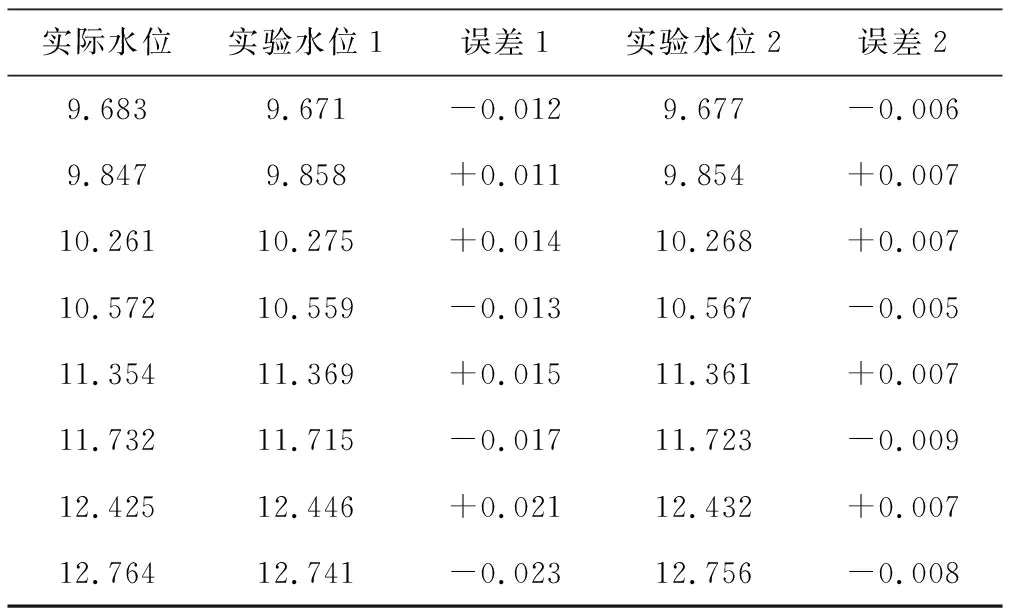
表1 实验结果对比 m

表2 温度变化实验数据Tab.2 Experimental data on temperature change

表3 湿度变化实验数据Tab.3 Experimental data on humidity change

表2和表3的实验数据表明在1 cm误差范围之内，测量精度不受环境温度和湿度的影响。

除温湿度外，由于气介式声波水位计常用于野外水位监测，所以传统的测量方式会受到风、波浪的影响，但在本设计中，可闻声波的传播是在相对封闭的波导管中，声波的传播不会受风向或波浪的影响。为了说明此情况，取安装于荆门某小型水库的该气介式声波水位计的实测数据进行分析，两天均无降雨，风力分别为1级和3级。具体数据如表4所示，在9∶00-12∶30时间段内，每0.5 h采集一次水位，中间一栏为风力为1级时的实测水位，右边一栏为风力为3级时的实测水位。

表4 风力实验结果对比Tab.4 Comparison of wind test results

5 结 语

本文阐述了一种气介式自校正声波水位计，该水位计采用对波形进行AD采集与sinc内插相结合的软件处理方法，使得系统在20 m测量范围内的绝对精度可以达到1 cm。且根据此前安装在荆门市某小型水库的水位计运行情况来看，测量结果基本不受环境温湿度变化及风力的影响，测量可靠性较高，实时水位、温湿度等信息可以上传至服务器，在实际运行中能够满足此类小型水库“低成本，稳定可靠，安装简便”的需求。