考虑线路恢复代价的机组恢复顺序优化

朱海南，于振江，李玉志，王 涛，王 琰

（国网山东省电力公司潍坊供电公司，山东 潍坊 261021）

0 引言

随着特高压交直流输电技术的发展，在电力系统中大量采用新技术的电力电子设备和元件，使得电力系统的规模日益扩大，动态行为愈加复杂，不断逼近电力系统的运行极限，由局部故障引发电力灾难的风险不断增加［1-3］。如2012-07-30，在印度发生了近10年来世界最大规模的停电事故。同时，近年来新能源发电技术，如风力发电和光伏发电技术迅速发展，大量接入电力系统，由于风力发电和光伏发电具有很强的随机性和不确定性，大量风电和光伏发电形式接入电力系统给电力系统正常运行带来极大的挑战，增加了电力系统发生事故的风险。电力系统发生大停电事故后，系统的恢复过程通常划分为3 个阶段［4-5］：黑启动阶段；网架恢复阶段［6］；负荷恢复阶段［7］。其中，黑启动阶段是整个恢复过程的起始阶段，也是整个恢复过程的基础阶段，是后续网架恢复和负荷恢复的保证，这一阶段的恢复目标是在尽可能短的时间内用黑启动机组作为起始电源，安全可靠地启动其余火电机组［8-10］。在黑启动阶段，最为重要的问题就是根据停电后系统所处的具体状态，有针对性地对机组恢复顺序进行优化安排，保证机组恢复过程安全可靠。

许多学者对机组恢复顺序问题进行了研究。文献［11-13］对发生大停电事故后的电网恢复过程中影响机组恢复顺序的各种因素和相关问题进行了详细的分析和讨论；文献［14］将机组恢复顺序优化问题建模为决策模型，使用层次分析法进行了求解，其中层次分析法中同时使用了定量指标和定性指标，并利用经验数据确定判断矩阵；文献［15］将机组排序问题建模为恢复过程中所有机组出力总和最大的优化问题，并用回溯算法求解该问题；文献［16-17］中则将机组恢复顺序优化问题建模为一个 “背包问题”，其优化目标设为系统恢复过程中，一个时间段内系统的总发电量最大，最后使用回溯算法进行了求解。文献［18］中将机组恢复排序问题建模为一个混合整数规划问题，将恢复过程中系统可提供的发电量最大设为优化目标。

对于机组恢复次序问题，大部分研究考虑的影响因素以及约束条件主要是机组本身的特征和约束，没有考虑机组恢复路径等网络约束。由于整个恢复控制十分复杂，充满了不确定性，仅考虑机组相关特性得出的机组恢复顺序可能不满足实际恢复过程的需要。在以上研究的基础上综合考虑了待恢复机组本身特性和机组恢复路径的网络约束，在分析了机组恢复过程中空载线路充电操作的各项约束基础上，定义了线路恢复代价的指标。以机组恢复过程中线路恢复代价倒数和机组可提供发电量的加和最大为优化目标，并采用加入交叉因子的改进粒子群优化（Particle Swarm Optimization，PSO）［19］算法和迪克斯特拉（Dijkstra）算法对所提出的优化模型进行了求解，最后用IEEE30节点系统作为算例进行了优化计算，其计算结果说明了算法的有效性，为机组恢复顺序优化提供了一种新的思路。

1 机组恢复顺序优化模型

1.1 线路恢复代价

在黑启动阶段，系统恢复过程包含的主要操作有启动黑启动电源，充电空载线路，启动待恢复机组辅机等［20］。以往对线路充电操作是否成功的判断标准主要是通过仿真校验其是否满足电气约束条件，由于恢复现场情况复杂多变，并且线路模型以及参数与实际线路存在一定差异，所以即便仿真校验满足约束条件，也不能保证现场空载线路充电操作一定成功。

在恢复空载线路时，需要进行空载充电操作，会产生持续工频过电压和操作过电压［21］等问题。其中，持续工频过电压是由于空载线路对地电容的存在，线路充电时会产生大量的充电无功，从而引发工频过电压。严重时，会引起发电机欠励或者自励磁等；空载线路的电压损耗公式为

式中：△U%为电压损耗，即线路始端电压和末端电压的数值差（U1-U2），与额定电压UN的比值；B为线路电纳；X为线路电抗。对于空载线路而言，如果线路本身电抗和对地电容过大，将会使线路末端电压超过安全限值。操作过电压是由于充电大量输电线路和投切电容器组引起的，严重时会引起线路的避雷器故障，操作过电压与系统总发电容量呈负相关，与线路的电抗和电容呈正相关关系［22］。

根据上述分析，对于空载线路而言，线路电抗和对地电容越小，空载线路充电时产生的工频过电压和操作过电压倍数就会越低，线路充电操作的成功率就会越高，同时系统发电容量越大，操作过电压也越低，线路恢复操作成功率也会越高，因此线路恢复代价主要与线路的电抗和电容呈正相关关系，与发电容量呈负相关关系。

定义线路恢复代价为

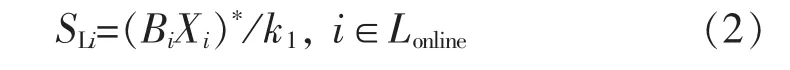
式中：SLi为第i条线路恢复代价；k1为当前时刻系统中发电总容量对线路恢复代价的影响系数；Bi为第i条线路的对地电纳，如果线路末端投入并联电抗器，则将并联电抗器的参数转化并入Bi中；Xi为第i条线路的电抗，（BiXi）*表示第 i条线路的 Bi和 Xi的乘积归一化处理后的数值；Lonline为当前时刻所有可用并且满足各项电气约束的线路集合，约束条件有工频过电压约束，操作过电压约束等。

1.2 目标函数

机组优化恢复过程中，一方面要考虑线路恢复代价，线路恢复代价越小，线路成功恢复的可能性越大；另一方面要考虑机组要在恢复过程中提供尽可能多的功率以加快系统恢复进程。将机组恢复顺序优化模型的目标函数设置为在机组在恢复过程中可提供的发电量和线路恢复代价倒数的加权和

式中：λ为比例系数；n为可用待恢复机组的具体数目；T为恢复控制总时间；Pj（t）为机组出力函数，如图1所示。优化目标为目标函数的函数值最大。

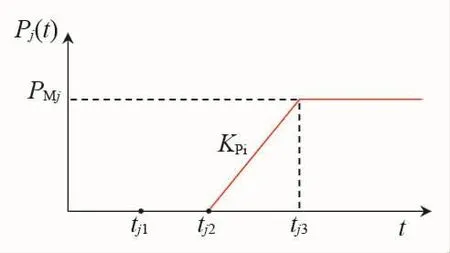
图1 机组出力函数

约束条件：

1）时间约束

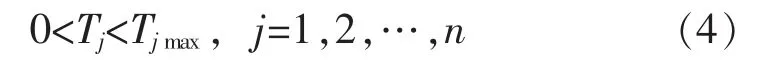
式中：Tj为第j台非黑启动机组从其余机组获得启动功率的时刻；Tjmax为第j台非黑启动机组考虑了裕量的机组热启动时限；如获得启动功率的时间间隔大于该热启动时限，则该机组需等待一段时间之后进行冷启动。

2）启动功率约束

式中：∑PG（t0）为 t0时刻系统中可用的总功率；Pcr（t0）为该时刻待恢复机组启动所需的功率。满足式（2）时，待恢复机组方具备重新启动条件。

3）潮流和节点电压约束

式中：PGi，QGi分别为第i台机组的输出有功和无功功率，PminGi、PmaxGi、QminGi、QmaxGi分别为机组 i有功和无功功率的上下限；n为已恢复机组的数目；nsn为当前机组恢复路径中包含的站点的具体个数；Pi为机组恢复路径中各条线路上流过的有功功率；Pimax为线路i的最大允许功率；Ui为节点电压。

2 优化模型求解

采用Dijkstra算法和加入交叉因子的改进PSO算法对所建立的机组恢复顺序优化模型进行求解。

2.1 Dijkstra算法

当系统中存在多个可用的黑启动电源点时，可在所有黑启动电源之间用一条权重为0的线路连接起来，形成一个虚拟的黑启动电源点［24］。

对于已经包含在其余机组恢复路径中的线路，其权重设为0，并相应修改权重矩阵中对应元素的数值［24］。

2.2 加入交叉因子的改进PSO算法

PSO算法［19］在连续空间优化问题中得到了广泛的应用。黑启动阶段机组恢复次序优化问题是一个离散优化问题，对于离散优化问题而言，解空间是离散点的集合，并非连续区域，不能直接使用PSO算法。文献［19］提出了一种改进的PSO算法，通过新的编码、解码方式将PSO算法进行了离散化，使之可以应用于离散优化问题。将文献［19］提出的改进PSO算法与遗传算法相结合，在PSO粒子更新时，加入了交叉操作，以提高离散PSO算法的收敛速度。

为了求解机组恢复顺序优化模型，要对离散PSO算法中的粒子进行重新编码。假设有5台待恢复机组需要进行排序，首先用离散数字1、2、3、4、5来一一对应5台待恢复机组在系统中的节点编号，5个数字的排列顺序就代表对应机组的恢复次序。粒子长度设置为5，粒子的每一位都用（0，1）之间的随机数来进行编码，对粒子的5个随机数进行大小排序，得出排序序列，然后根据离散数字编码和机组对应关系进行解码，得到解码序列即机组恢复次序［19］，如图2所示。

图2 粒子编码与解码

采用的交叉方法为：选出两个待交叉的粒子o1和o2，从o2中随机选择除第一维之外的任一维到倒数第二维为交叉区域c，将o1和o2中出现在c中的数字删除，并将c加到o1的前面和o2的后面，如果此时粒子的维数大于5，则删除粒子最后多余的几维， 如 o1＝｛0.12 0.21 0.34 0.56 0.79｝，o2＝｛0.34 0.39 0.42 0.91 0.56｝，随机选取交叉区域为c＝｛0.39 0.42 0.91｝， 交叉 后 o1＝｛0.69 0.42 0.91 0.12 0.21｝，o2＝｛0.34 0.56 0.39 0.42 0.91｝。

使用加入交叉操作的离散PSO算法求解机组恢复顺序优化模型的具体步骤为：

1）将算法中所用的各项参数进行初始化，设定粒子总数为nP，规定迭代次数为nmax，随机产生nP个初始粒子 X0， 并初始 PSO 算法中的 c1、c2、w、D 等参数；

2）对当前粒子进行解码得到该粒子表示的机组恢复次序，调用Dijkstra算法搜索黑启动电源点到各个机组的恢复路径，并计算相应的目标函数值，找到各个粒子的个体极值pbest，个体极值位置pxbest，全局极值gbest以及全局极值位置gxbest；

3）对每个粒子对应的目标函数值进行排序，目标函数值满足要求的粒子一般直接进入下一代；目标函数值不满足要求的粒子进行交叉操作，并与交叉操作前粒子的目标函数值进行比较，滤掉目标函数值变差的变异，从而得到新一代PSO粒子；

4）计算出粒子群中每个粒子的速度，并更新每个粒子的位置，转到步骤2），直到迭代次数达到nmax，最后输出gbest和gxbest。

3 算例分析

采用Matlab语言进行仿真计算，并采用了IEEE30节点系统［25］，编制了考虑线路恢复代价的机组恢复优化程序。IEEE30节点系统算例中共包含6台发电机，41条线路，该系统如图3所示。在图3中，线路上标注的数值表示恢复该条线路所需要的操作时间，单位为min。

为了证明算法的有效性，设定节点27机组的热启动时间为10 min。如果在热启动时限内，节点27机组不能获得启动功率，则该机组只能在1 h后才可以进行冷启动。其余机组热启动时间设定为30 min。设定改进的PSO算法中，粒子数np=20，最大迭代次数nmax=100。设定图3中节点1机组具备黑启动能力， 节点 2、13、22、23、27 上机组不具备黑启动能力，为待恢复的机组节点。

按照提出的优化模型以及相关的求解步骤，对IEEE30节点算例进行了仿真计算，其计算结果如表1所示。表1给出了机组启动的几种次序，其中方案1为最优次序。

表1 系统机组恢复次序

4 结语

定义一种衡量线路恢复代价的指标来表示线路进行恢复操作时的成功概率。综合考虑了机组在发生大停电事故后重新启动过程中的各种约束条件，以线路恢复代价的倒数和所有机组在恢复过程中可提供的发电量的加权和最大为优化目标，建立了机组恢复顺序优化模型。使用加入交叉操作的离散PSO算法，并结合Dijkstra算法对该优化模型进行了求解。使用IEEE30节点系统进行了仿真计算，其仿真结果验证了所提算法的有效性。通过考虑机组恢复路径中线路恢复代价，保证了以优化结果为指导制订的恢复方案的可行性，对实际机组恢复方案的制订提供了一种新的思路。