考虑支路可靠性过程的网络节点状态仿真

张 璇

(天津泰达电子工程有限公司 天津 300450)

0 引 言

电力系统可靠性是通过定量的可靠性指标来衡量的。在一般性的可靠性分析方法中，电力系统的可靠性指标——故障率λ、故障修复时间 t及年停电时间u等均由元件的基本可靠性指标求得。在这里就出现了一个近似条件，即认为当支路(设备)状态变化满足齐次马尔可夫过程特点时，节点状态变化同样满足，所以才有了通过支路(设备)可靠性指标去求节点指标的各种方法，但其中网络节点的状态变化是否符合条件并未有相应的解释。

因此，本文拟应用计算机软件，在不考虑容量约束的情况下，通过仿真设备(支路)的状态变化对网络节点状态的影响，来判断节点状态变化是否符合或者近似符合齐次马尔可夫过程。

1 网络节点与支路状态的可靠性分析方法

1.1 马尔可夫(Markov)过程简介

可修系统模型是一种重要的可靠性模型，因其引入了允许设备修复的概念，使系统可靠性研究得以更加完善。假定设备的故障率λ和修复率μ均为常数，则各部件的故障分布和修复时间分布均为指数分布，在这种条件下，总可以找到适当的系统状态，以使用马尔可夫过程描述[1]。基于马尔可夫过程的这类可修系统是可靠性分析中研究及应用最多的一类系统。

1.1.1 马尔可夫过程的定义

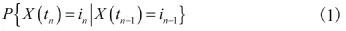
则称随机过程{ X (t), t ≥ 0 }为连续时间、有限状态空间的马尔可夫过程。

若对任意t，u≥0，均有：

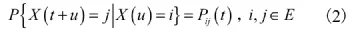
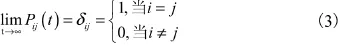
若用Pj(t)表示t时刻系统处于状态 j的概率，则：

对于此处描述的有限状态空间 E的齐次马尔可夫过程，以下极限存在且有限。

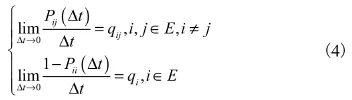
1.1.2 马尔可夫可修系统模型

存在一个可修系统，在t时刻所处的运行状态可以用 X (t)来表示。该存在N+1个运行状态，其中状态 0，1，…，K是系统的正常工作状态；K+1，…，N是异常故障状态。记假定所表示的马尔可夫过程为齐次的，且在足够小的时间Δt内的转移概率函数满足：

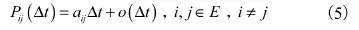
显然：

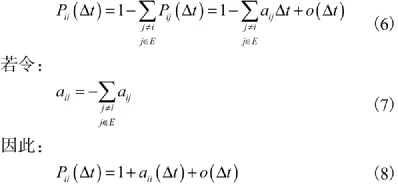
则由式(4)可知：

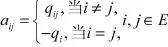
在系统的可靠性分析过程中，各类可靠性指标就可以通过上述齐次马尔可夫过程的一般应用模型来求得。

1.1.3 系统的可用度

系统在任意时刻t，处于可用状态的概率称为系统的可用度。下面对用马尔可夫过程分析可修复系统瞬时和稳态可用度的方法及过程作一些介绍。

①瞬时可用度

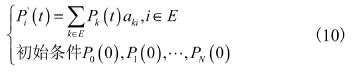
公式(10)可以写成矩阵的形式：

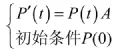
②稳态可用度

系统的稳态可用度是评估系统可靠性的重要依据，与瞬时可用度相比，工程实践更加注重系统的稳态可用度。可以运用 P (t)的极限分布来求得系统稳态可用度，此处引用以下结果[2]。

由式(5)和(8)，可知定理1的条件满足。由于：

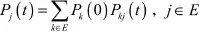
当t→∞时，根据定理1，上式右端极限存在，因而左端的极限也存在，且：

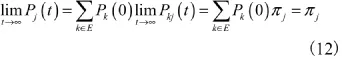
定理2，系统的稳态可用度为：

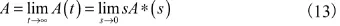
这样，稳态可用度A就可以通过瞬时可用度A(t)来计算。

1.1.4 分析马尔可夫型可修系统的步骤

给定一个满足上述定义条件的具体的马尔可夫型可修系统，可通过以下步骤求得系统的各项可靠性分析指标。①定义系统的状态，并保证该状态能够完整地表示并区分系统的正常和故障运行情况。令为系统的状态集合，分别表示系统正常运行状态的集合和故障状态的集合。②定义t时刻的随机过程。若各部件的故障分布和修复时间分布均为指数分布，则该随机过程是一个有限状态空间E上的齐次马尔可夫过程。③求转移率矩阵A。对前面定义的随机过程 X (t)，可以求得转移概率函数：

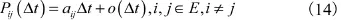
进一步写出转移率矩阵：

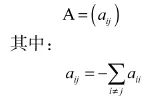
④求解 Pi(t)=P{X(t)=j}，j∈E。解微分方程组：

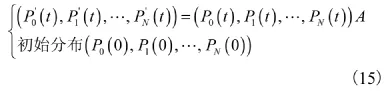
可以利用拉氏变换的方法，先将其转化为线性方程组求解，再作反变换，得出微分方程组的解。⑤求系统的瞬时可用度和稳态可用度。由上述介绍可知：

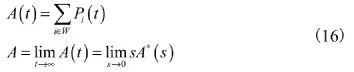
1.2 系统网络可靠性的计算方法

系统节点可靠性的分析是在元件故障和修复数据以及系统结构的基础上，求得的能够表明系统可靠性的定量指标[3]。目前，研究系统网络可靠性的基本分析方法主要有两种：解析法和蒙特卡洛模拟法，下面分别予以简要介绍。

1.2.1 解析法

解析法基于马尔可夫模型，常用于一些简化了的或小型的组合系统的可靠性评估，通过建立并求解电力系统的可靠性分析数学模型，从而计算得出系统的可靠性分析指标。

这种计算方法的优点在于利用了精确的数学模型，概念清晰，易于理解，且逻辑关系明确，模型的精度较高；其缺点是当系统规模较大时，计算量便会随着系统复杂程度的增大呈现指数增长。因此解析法仅适用于系统网络规模较小，元件数目不太多但故障时有重大影响的情况。

解析法中应用较为广泛的主要有网络法、故障树分析法(Fault Tree Analysis)和状态空间法。至于具体选择何种方法，则需要根据系统结构和规模、元件的独立性和可修复性、故障时间及修复时间的概率分布(指数或非指数分布)、故障模式(独立、相关或共同模式故障)以及运行方式和环境的影响等[3]进行判断。下面仅对本文算例中用到的状态空间法进行简要介绍。

系统某一时刻所处的状态取决于系统中各元件的状态。系统网络中的元件一般为两状态元件：正常工作状态或异常故障状态。对于一个给定的系统网络，可能出现的所有可能的状态集，就称为状态空间，其中任何一个元件的状态发生变化，都将使系统从当前状态转变为另一个状态。

所谓状态空间法，就是用系统所处的状态和这些状态之间可能发生的转移来表示系统，并由故障判据划分出系统正常工作状态和故障状态，以求得系统的可靠性指标[3]。

在元件的故障密度函数和修复密度函数服从指数分布的情况下，元件的故障率和修复率都是常数，便可以应用齐次马尔可夫过程来描述系统的状态变化，对其求解来得到各项可靠性指标。对于规模较小的系统网络，状态空间法的基本计算步骤如下：列举出所有可能的系统状态，并规定系统故障判据；根据元件的两状态概率计算系统处于某一状态的概率；分析各状态之间如何转换，并根据计算出的转移概率，画出系统状态转移联络图；按照规定的故障判据，将各种系统状态进行分类(一般可靠性分析中只需将各种系统状态分为正常和故障两大类)，然后逐个检验其事故后果，针对某一类状态计算系统的可靠性指标[4]。

本文所讨论的“考虑支路可靠性过程的网络节点状态仿真”，针对具体问题所用到的状态空间法的分析过程不尽相同。

1.2.2 电力系统可靠性评估的模拟法

模拟法又称随机抽样方法，其本质思想就是一种概率模拟的方法：为了求解一个问题，首先建立一个概率模型或随机过程，使它的参数等于问题的解，然后通过对模型或过程的观察或抽样实验来计算所求参数的统计特征，最后给出所求问题的近似解，并给出解的精度或误差[3]。蒙特卡洛模拟法的优点是模型简单，省去了复杂的数学推导和演算，比较直观，易于理解和掌握，因此该方法在电力系统可靠性评估中的应用得到了快速发展，并逐渐成为可靠性评估的重要方法[5-7]。

2 网络节点可靠性仿真算例

2.1 仿真网络模型介绍

本文所采用的仿真实例是由24个单元设备组成的网络结构，其结构如图 1所示。其中，A、B节点为电源节点，向网络中供电，C节点为负荷节点。假设设备正常工作时为0状态，故障时为1状态。

从该网络图中我们可以得到如下信息：支路数14条；使负荷节点 C可以正常工作的所有最小路状态容易得知。

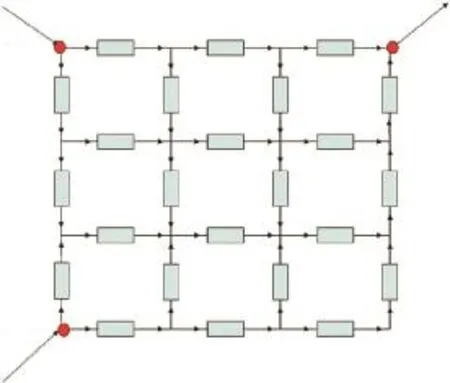
图1 仿真网络模型Fig.1 Simulation network model

仿真程序中的一个输入变量即是这14个能够使负荷节点 L正常工作的最小路的状态，即只要在每个状态中相应元件为 0，系统就可以正常工作，不论其他元件的状态是 0或者 1。在仿真程序中，我们允许2个及以上设备同时发生故障。

对于每个单元设备，为了简化分析过程，我们假定其故障率λ和修复率μ均相同，且为常数。用MATLAB软件进行程序仿真。仿真程序的输入变量为负荷节点能够正常工作的最小路状态集 P、系统运行时间T以及设备数量N。输出变量STA为负荷节点L在所有运行时间中在每一段时间的状态(0状态和 1状态)，以及系统在相当长一段时间内的稳态可用度A，同时还能够生成稳态可用度A随时间t的变化关系图。

仿真流程图如图2所示。

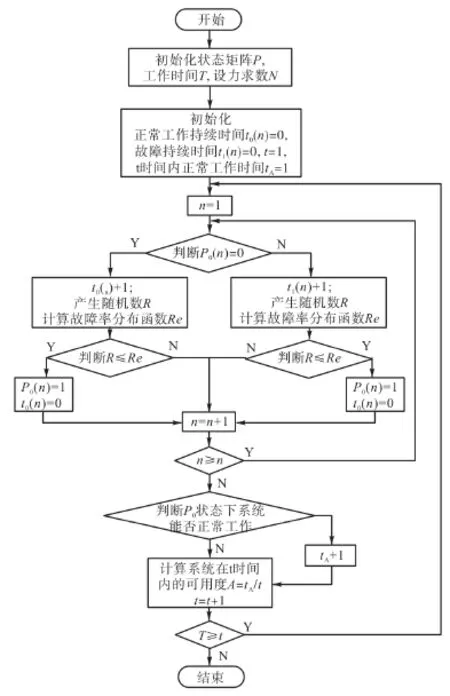
图2 仿真流程图Fig.2 Simulation flow chart

2.2 仿真结果统计与分析

仿真结果得到的系统稳态可用度 A的变化规律如图3所示。

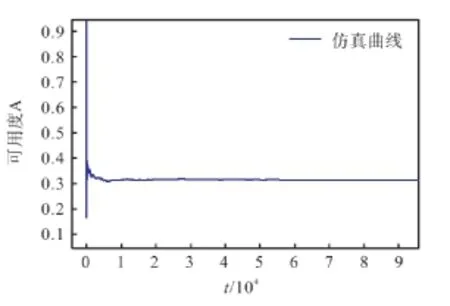
图3 可用度变化曲线Fig.3 Availability change curve

从理论与实验图的对比中，我们可以看到，稳态可用度A随时间t的变化分布规律是大致相同的。此外，在 t很小的时候，可用度 A在局部有小的波动，而由理论值得到的图是十分标准的呈 e的负指数次幂衰减的曲线。

3 结 论

在一般性的可靠性分析方法中，网络节点的可靠性指标——故障率λ、故障修复时间r及年停电时间u等均由元件的基本可靠性指标求得。针对许多实际应用中直接假定网络节点的状态变化与设备状态变化规律相同，都满足齐次马尔可夫过程而未加证明的问题，本文作了相关研究和讨论，得到以下结论：在设备(支路)的状态变化满足齐次马尔可夫过程的条件下，网络节点的状态变化也基本满足齐次马尔可夫过程的假设是成立的，并且偏差数值在可接受的范围之内；以往计算中所假定的情况，根据齐次马尔可夫过程的计算条件，在每一个tΔ的计算时间内，最多只有 1个设备发生故障，但由实验结果可以看到，在允许2个及以上设备同时发生故障的情况下，所得到的网络节点可用度依然按照 e的负指数次幂衰减的曲线规律变化。因此，在实际的可靠性评估计算中，为了简化工作量，可以将2个及以上设备同时出现故障的概率认为是零，这对于评估结果不会产生较大的影响，可以得到相对准确的可靠性指标。