两种移动列车脉动风速时程模拟方法对比分析
2018-08-01刘书军邹淇炀
刘书军,肖 军,邹淇炀
(1.重庆交通职业学院,重庆 402247;2.重庆交通大学 土木工程学院,重庆 400074;3.西南交通大学 桥梁工程系,四川 成都 610031)
穿越随机风场的高速列车所感受到的瞬时风速与其所处空间位置和时间相关,在某确定时刻,空间位置与运行速度有关,因而移动点脉动风速谱与列车运行速度有关。由于随机风场并非各向同性,因而移动点脉动风速谱还受来流风向角以及由车速和平均风速所形成的偏航角影响。穿越随机风场的高速列车所感受到的脉动风的特性区别于静止点脉动风的特性,其风速时程的模拟不能采用静止点风速谱直接进行样本时程的模拟。以往在模拟运动车辆所感受到的脉动风时程时,通常采用以下2种方法:
1)采用固定点的多变量随机过程模拟方法。首先,利用多变量随机过程模拟的方法模拟得到离散随机风场;然后,采取离散点提取或者相邻点插值的方式获取列车当前位置的瞬时风速,并通过增加模拟点数来弱化人为离散引起的误差。
2)基于移动列车的脉动风速谱直接进行单变量随机过程模拟,以获取移动列车的风速时程样本。
第1种方法是一种间接模拟的方法,适用于需要同时模拟固定点风场和移动点风速时程的情况。例如,在进行风-车-桥耦合振动分析时,需要同时模拟静止桥梁所感受到的离散风场,以及移动列车所感受到的随机风速时程。在不需要模拟固定离散风场的情况下,例如在进行风-车-线耦合振动分析时,仅需要模拟移动列车所感受到的脉动风速时程,则采用第2种方法能够显著提高模拟效率。本文主要介绍上述2种移动列车脉动风速时程模拟方法,并对比2种方法的模拟效率以及功率谱的吻合情况。
1 基于多变量随机过程的风速时程模拟
1.1 传统的谱分解方法及其快速算法
多变量随机过程模拟方法主要包括:谱分解法、线性滤波法、小波方法等[1-3]。其中谱分解法广泛应用于随机风场模拟。
一维n变量0均值的高斯平稳随机过程fj0(t)(j=1,2,…,n)的互功率谱矩阵可写为
(1)
fj0(t)的样本函数可以根据下式进行模拟:
(2)
式中:Δω为频率间隔,ωl=Δω(l-1);N为频率分段数;φml为0~2π之间独立均匀分布的随机数;θjm为相位角,计算式为
(3)
下三角矩阵H(ω)满足
(4)
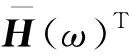
传统谱解法的模拟过程大致可以分为2个阶段。第1阶段为互谱密度矩阵的Cholesky分解;第2阶段则进行谐波的叠加运算。经典的多变量随机过程模拟方法由于在每一个频率点处都需要做一次Cholesky分解,且需要将所有频率点分解得到的H(ω)矩阵存储下来,因而存在显著的计算效率和计算内存问题。图1反映了频率分段数1024时在个人电脑上模拟点数量对模拟时长的影响。
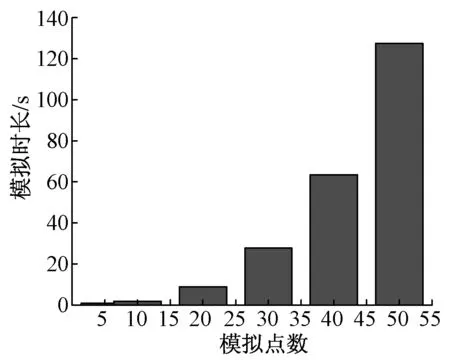
图1 模拟点数量对模拟时长的影响
由图1可见模拟点数对模拟时长影响显著。在计算过程中发现,在当前电脑配置下如果模拟点数超过50,则由于内存占用问题几乎无法完成模拟。基于谱解法的特点,在第1阶段分解互谱密度矩阵Cholesky分解的过程中,计算机内存占用问题突出,因为每一个频率点Cholesky分解得到的H(ω)矩阵都需保存。由式(2)可知,对每个频率分量ωl进行余弦叠加时都需要进行一次Cholesky分解,当模拟点数增加时严重影响模拟效率。
为解决传统谱解法存在的计算效率和计算内存占用问题,文献[4]基于谱解法的特点,在第1阶段分解互谱密度矩阵Cholesky分解的过程中给出风场互谱密度矩阵分解的解析表达式。这一方式使得H(ω)不需要事先生成,而只在需要时调用解析表达式。这直接解决了对计算内存的占用问题。文献[5]基于文献[6]的方法,提出了一种改进的适用于模拟短时随机脉动风场的数值模拟方法,极大地加快了谱解法在第2阶段的计算效率。文献[7-10]通过不同的方式对互谱密度矩阵分解做了大量改进,有效提高了谱解法的模拟效率。
本文在文献[4-5]的基础上,编制了随机风场快速模拟程序WindEMSSP。该程序在谱解法第1阶段采用了解析的表达式,在第2阶段采用文献[5]所改进的逆向快速傅里叶变换(IFFT)技术。
假定需要模拟的是离地相同高度的等间距的n个水平点的随机风场,则各点的水平风速谱相同,即
(5)
采用相干函数表达互功率谱,表达式为
(6)
式中:Δjm为j点和m点之间的水平距离;Coh(Δjm,ω)为相干函数。
假定各点之间间距相等,且均为Δ,则Δjm=Δ·|j-m|,采用Davenport相干函数,得到
(7)
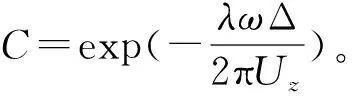
因而可以得到互功率谱矩阵为
(8)
对互功率谱矩阵进行Chelosky分解,H(ω)可以显式地表达为
(9)
式中
G(ω)=
(10)
式(10)写成解析表达式为
(11)
式(11)给出了风场互谱密度矩阵分解的解析表达式。这一方式既解决了对计算内存的占用问题,且由于不需要进行大量的Cholesky分解,对计算效率也有显著的提高。
在谱解法的第2阶段,WindEMSSP程序利用在频域内对分解的相干矩阵进行叠加运算形成复共轭对称序列的方法,因而随机过程样本只需要一次IFFT即可实现,也即一维n变量随机过程模拟仅需执行n次IFFT变换。而采用单索引方法和双索引方法模拟全部随机过程所执行的IFFT的次数则为n·(n+1)/2。
1.2 基于随机风场插值的列车风速时程模拟
高速列车在随机风场中运动,其所感受到的风速时程如图 2所示。瞬时风速等同列车当前位置、当前时刻静止点的瞬时风速。
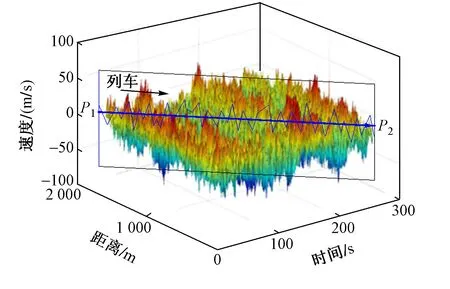
图2 基于随机风场插值的列车风速时程模拟示意
由图 2可见,移动列车所感受到的风速时程,可通过2个步骤获取:①将列车运动所经过的空间区域进行空间离散,并采用多变量随机过程模拟的方法得到固定点的离散随机风场;②采用时间和空间插值的方式,由固定点的离散随机风场插值得到运动列车所感受到的随机风速时程。
为模拟离散随机风场,首先需要给出静止点脉动风速谱。本文采用Simiu谱[11],即
(12)
(13)
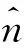
继而利用本文编制的随机风场快速模拟程序WindEMSSP,模拟得到1024个离散随机点的风速时程样本的随机风场,模拟总耗时474.74 s,模拟得到的离散随机风场如图3所示。

图3 模拟得到的离散随机风场
任取一条模拟时程,估算得到其功率谱,将它们与静止点理论功率谱进行对比,结果如图4所示。
分别选取点1和点20,对比自相关和互相关函数模拟值与理论值,结果如图5所示。
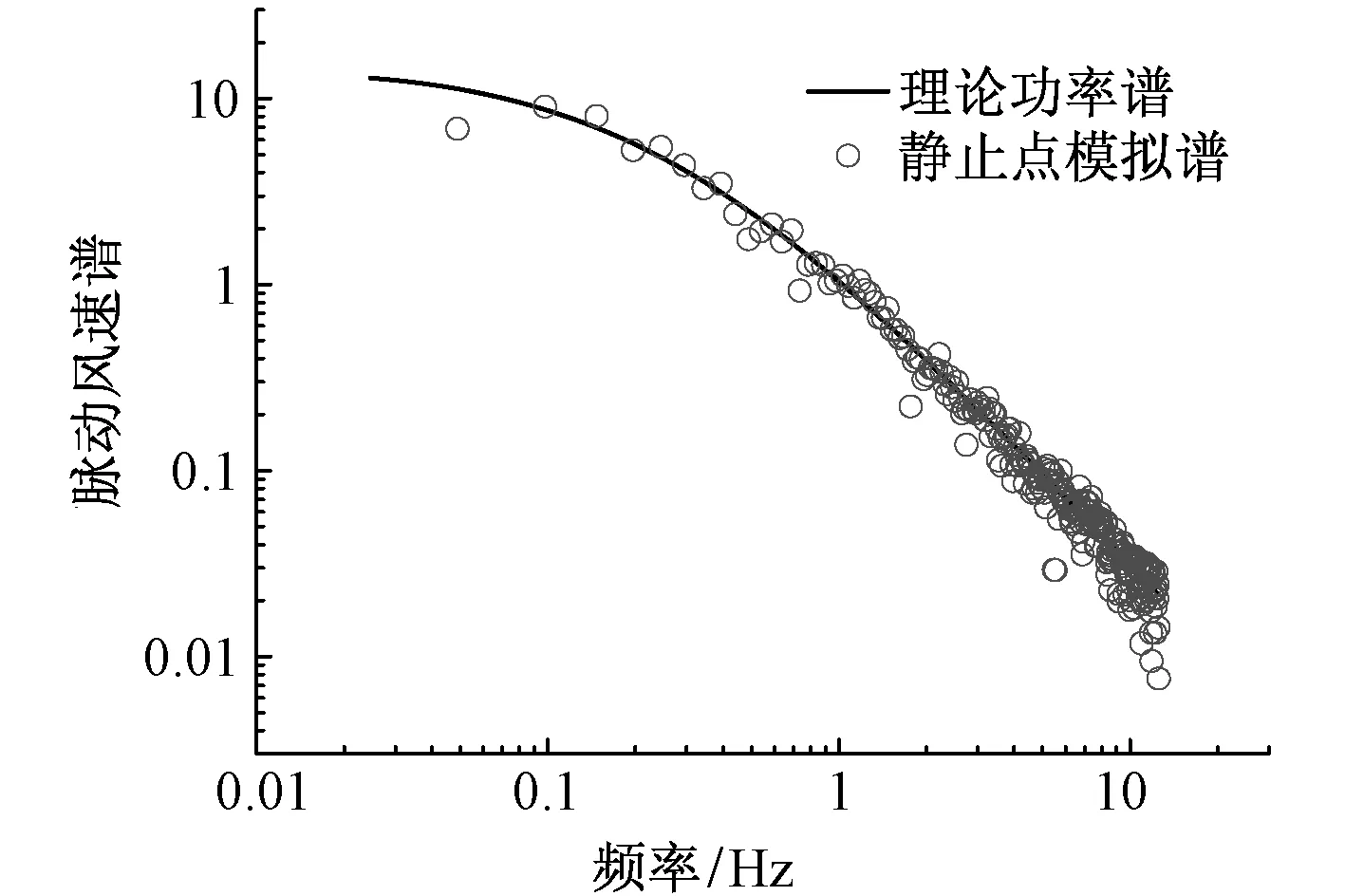
图4 模拟点功率谱与理论功率谱对比
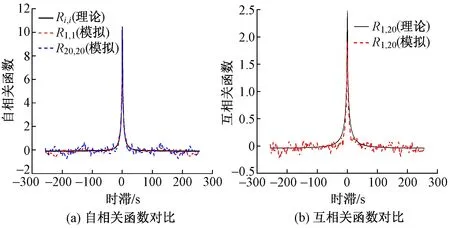
图5 自相关函数、互相关函数对比
假设列车以288 km/h的速度穿过模拟得到的离散随机风场,插值得到列车所感受到的随机风速时程,结果如图6所示。
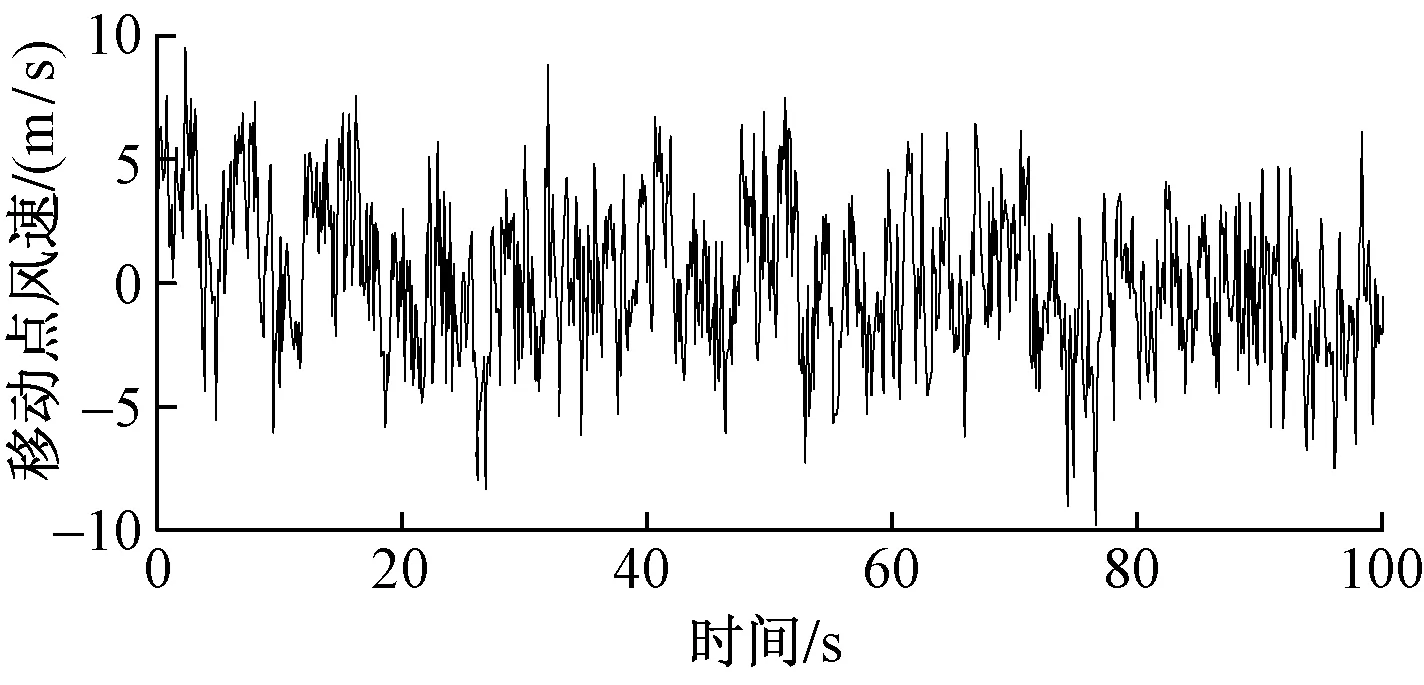
图6 插值法得到的移动点风速时程
2 基于移动风速谱的风速时程模拟
为了要获取移动列车的一条风速时程而采用多变量随机过程模拟的方法是效率低下的。移动列车的一条脉动风速时程对应着移动单点的脉动风速谱;反之,如果可以通过某种途径获取考虑列车运动情况下的脉动风速谱的表达式,则可以利用单变量随机过程模拟的方法直接进行模拟。
2.1 考虑列车运动的移动点脉动风速谱
COOPER[12]基于湍流泰勒假定及各向同性湍流假定,推导得到了考虑列车运动的移动点脉动风速谱(列车运动方向与风速方向垂直,Karman谱)。文献[13]基于Simiu谱推导得到了列车以任意方向运动的移动点脉动风速谱的半解析表达式。文献[14-15]则推导得到了基于任意脉动风速谱表达式及任意列车运动方向情况下的移动点脉动风速谱的解析表达式。其形式为
(14)
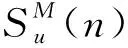
由式(14)可知,考虑列车运动情况下的移动点纵向脉动风速谱可由静止点纵向和侧向脉动风速谱通过平移和叠加得到。移动点脉动风速谱明显区别于静止点风速谱,因而移动点脉动风速时程的模拟不能直接采用静止点风速谱表达式。
本文采用式(14)作为考虑列车运动情况下的移动点纵向脉动风速谱的理论表达式。
2.2 基于移动风速谱的单变量随机过程模拟
在获取考虑列车运动情况下的脉动风速谱后,可直接利用单变量随机过程模拟的方法直接模拟得到移动点脉动风速时程。
算例:采用Simiu谱,模拟总时长为800 s,模拟点时间间隔0.1 s,移动点速度288 km/h,平均风速20 m/s。模拟得到移动点脉动风速时程及模拟功率谱和理论功率谱对比分别见图7、图8。可见,采用单变量随机过程模拟方法获取的移动点脉动风速时程其估计功率谱与理论功率谱对比良好。
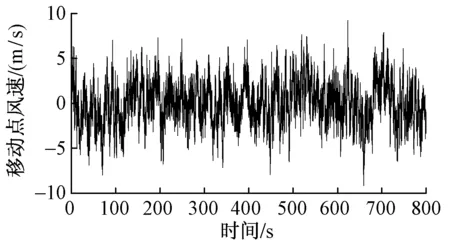
图7 直接法模拟得到的移动点风速时程
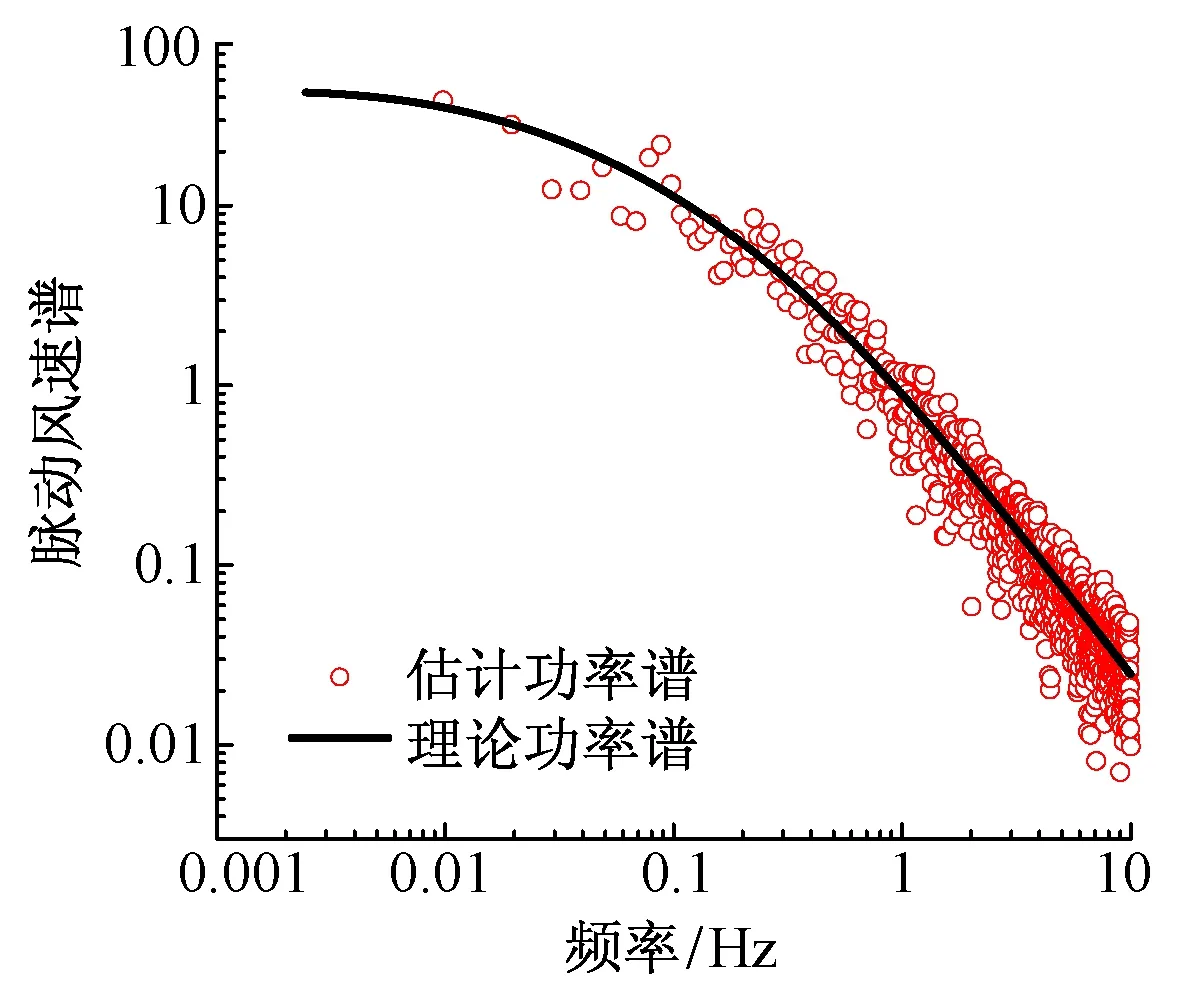
图8 移动点脉动风速谱对比
3 2种模拟方法对比
移动点的脉动风速时程可以由静止随机风速场通过时间和空间插值的方式获取。如果移动列车的脉动风速时程在所有时刻点的空间位置处都对应一个静止随机风场模拟点,则移动点风速时程的获取就避免了空间插值引入的误差。其功率谱估计值即可较为真实地反映移动列车的脉动风速谱。对2种不同的移动点脉动风速时程模拟方法进行对比,计算参数见表1。
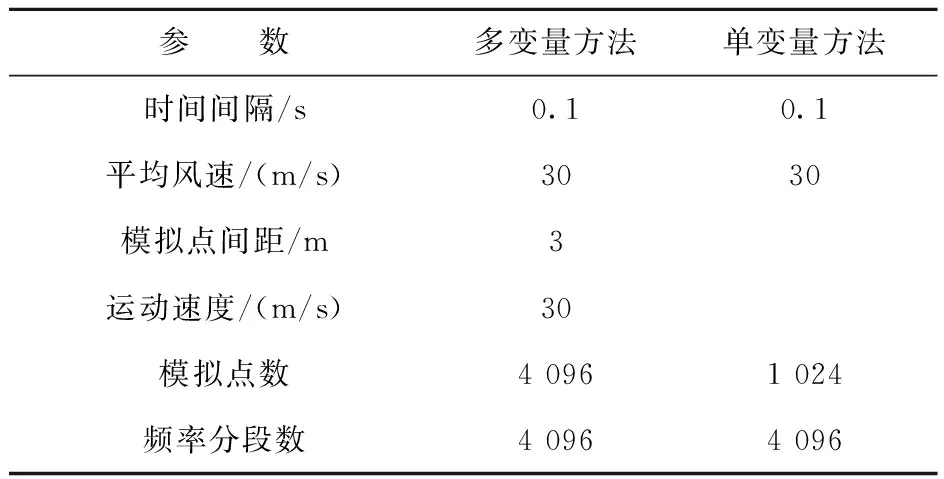
表1 计算参数汇总
利用2种不同方法模拟得到的移动点脉动风速时程进行功率谱估计,并与式(14)给出的移动点脉动风速谱的理论值进行对比,结果见图9。
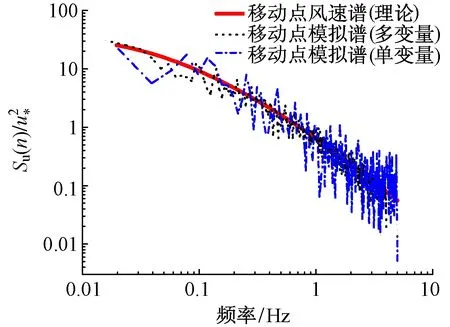
图9 2种不同模拟方法的功率谱对比
由图9可见,采用不同方法模拟得到的移动点脉动风速时程,其模拟功率谱均与理论功率谱吻合较好,表明2种方法都能满足模拟需要。
图10对比2种方法在计算效率上的差异。其中多变量随机过程模拟方法采用本文基于快速算法编制的WindEMSSP程序进行计算。
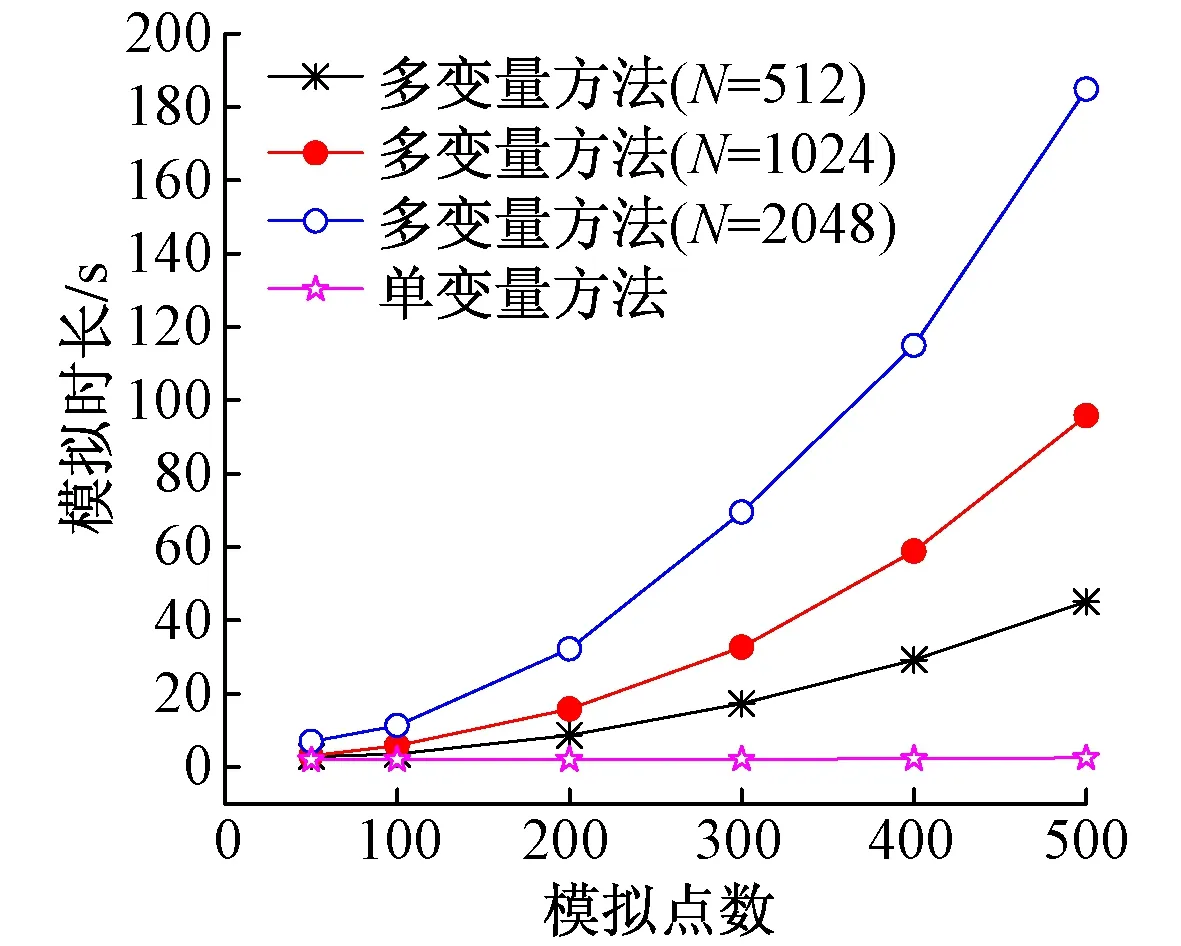
图10 计算效率对比
由图10可见,尽管采用了快速模拟算法,但随着模拟点数的增加,多变量随机过程模拟的效率依然显著降低,而单变量模拟效率几乎不受影响,不同频率分段数下大致计算时长均约为2.0 s。显然,基于可靠度理论,采用单变量随机过程模拟的方法在模拟效率上具有明显优势。
4 结论
本文介绍了2种不同的移动点脉动风速时程模拟方法即采用固定点的多变量的随机过程模拟方法和基于移动列车的脉动风速谱直接进行单变量随机过程模拟的方法,分别适用于不同的风场模拟的需要。主要结论如下:
1)2种方法模拟得到的移动点脉动风速时程,其模拟功率谱与理论功率谱均吻合良好,均可以得到不同车速下移动点的风速时程。
2)利用移动脉动风速谱解析表达式,基于单变量随机过程模拟的方法较传统多变量随机过程模拟方法,模拟效率明显提高。这对于基于可靠度的侧风作用下的高速列车安全性和舒适性评价具有重要意义。
