考虑行波效应的大跨度结合梁斜拉桥地震响应分析

许智强,赵人达

(西南交通大学 土木工程学院，四川 成都 610031)

随着我国大跨度桥梁的快速发展，其抗震问题成为国内的研究热点。地震动传播时在时间和空间上变化较大，对大跨度斜拉桥的地震响应影响较大[1-5]。对于大跨斜拉桥，由于地震波沿桥纵向先后到达的时间差，引起各支承处输入地震时程的相位差，简称行波效应[6-7]。

近年来，针对多点激励作用下大跨斜拉桥的地震响应，国内外学者采用多种方法进行了研究。王再荣等[8]对多点激励下的振型方程进行推导，采用振动分析法研究行波效应对大跨斜拉桥的振动机理。陈清军等[9]采用改进虚拟激励法研究行波效应对超大跨斜拉桥的影响，结果表明考虑行波效应使大跨斜拉桥位移和弯矩响应减小。方圆等[10]采用动态时程分析法对大跨多塔斜拉桥的行波效应进行了研究，结果表明在塔梁固结情况下行波效应影响较大，而塔梁无约束时行波效应影响较小。

本文以西部山区的西固黄河大跨结合梁斜拉桥为例，采用ANSYS软件建立有限元模型，基于非线性时程分析法研究行波效应对大跨度结合梁斜拉桥地震响应的影响。

1 工程概况及动力分析模型

1.1 桥梁概况

西固黄河大桥是兰州南绕城高速公路上跨越黄河、兰新铁路的重点工程。场地基本地震动峰值加速度为0.2g，场地条件为Ⅱ类，特征周期Tg=0.4 s。其主桥为跨径(67+110+360+110+67)m的工字钢-混凝土结合梁斜拉桥，桥塔采用钢筋混凝土菱形塔，桥塔高151 m，是西北地区在黄河上跨度最大、塔身最高的斜拉桥。西固黄河大桥总体布置见图1。主梁采用工字钢-混凝土结合梁，结合梁高2.83 m(钢主梁中心处)，钢主梁采用 2 500×1 000×36(60)×20 mm工字形截面，主梁断面见图2。

图1 西固黄河大桥总体布置(单位：m)

图2 主梁断面(单位：mm)

1.2 有限元模型

基于有限元软件ANSYS建立全桥空间有限元模型。桥塔、桥墩及主梁采用Beam 188梁单元模拟，桥面铺装等采用集中质量单元Mass 21附加在主梁节点上，斜拉索采用Link 10单元模拟，使用Ernst公式考虑斜拉索的垂度效应对其弹性模量进行修正。模型中采用土弹簧模拟桩土相互作用，其等效弹簧刚度采用m法[11]计算。

1.3 动力特性分析

利用多重Ritz向量法计算该桥动力特性，前8阶结构自振频率及振型特征见表1。可知，结构基频为0.171 3 Hz，基本周期为5.838 s，属于长周期柔性结构。主梁1阶振型为纵飘和反对称竖弯，2,3阶振型为主梁侧弯，说明主梁纵桥向刚度较小且低于横桥向刚度。桥墩在4,5,7阶振型中出现密集情况，表现为各墩的纵向弯曲，说明桥墩纵向刚度较小。

表1 结构自振频率及振型

2 地震动输入

采用以规范设计水平加速度反应谱为目标拟合而成的人工地震波进行抗震计算。计算主要针对E2地震作用即50年超越概率为2%的地震作用，利用反应谱转人工地震波程序SIMQKE_GR生成3条地震波，见图3。每条波之间的相关系数小于10%，地震持时30 s，阻尼比取0.03。基于人工地震波时程曲线的反应谱与设计水平加速度反应谱对比见图4。可见二者吻合度较好，可用于抗震计算。

为研究多点激励下波速对结构地震响应的影响，依次取500，1 000，2 000，3 000，4 000 m/s和无穷大(即一致激励)6个地震波速进行时程分析。由于结构的对称性较好，本文仅考虑地震波由南向北传播。

图3 人工地震波加速度时程曲线

图4 人工地震波拟合反应谱与设计水平加速度反应谱对比

3 行波效应的影响分析

3.1 塔顶与主梁位移响应分析

为研究行波效应对大跨斜拉桥位移响应的影响，选取主梁跨中节点和塔顶节点，分别比较不同波速的非一致激励与一致激励对其位移响应的影响，对比结果见图5。可知：对于主梁与塔顶纵向位移，行波效应总体上使其响应减小。当波速为500 m/s时，非一致激励下主梁、塔顶纵向位移分别为一致激励下的75%,93%;随着波速的增大，纵向位移不断增大，逐渐趋于一致激励，当波速达到 3 000 m/s后，行波效应对结构地震响应影响较小，位移变化平缓。

图5 纵向位移对比

3.2 墩底塔底截面内力响应分析

地震动行进波速变化对塔底截面、墩底截面内力响应的影响分别见图6和图7。纵坐标为考虑行波效应时非一致激励与一致激励对应截面响应的比值。

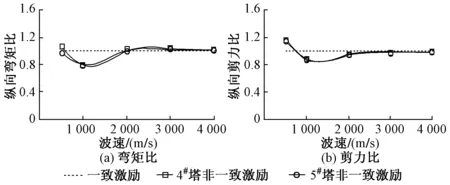
图6 塔底截面内力比

图7 墩底截面内力比

由图6、图7可以看出：①考虑行波效应后塔底截面的弯矩及剪力总体上比一致激励要小，当波速为 1 000 m/s时，弯矩减小20%，剪力值也从开始的增大18%减小为一致激励的80%；当波速大于 2 000 m/s后弯矩与剪力值与一致激励基本相同。②对于2#和3#墩底截面，当波速为500～2 000 m/s时，考虑行波效应的墩底截面弯矩增大约15%～5%，之后对弯矩影响较小;当波速为500 m/s时剪力值增大约19%，当波速大于 1 000 m/s后剪力值趋于一致激励。

3.3 墩梁与塔梁相对位移响应分析

图8 墩梁及塔梁相对位移

考虑行波效应的非一致激励和一致激励下墩梁和塔梁顺桥向相对位移见图8。可知，考虑行波效应后墩梁和塔梁相对位移均有所增大，墩梁相对位移增大约60%，而塔梁相对位移增大了20%。主要是由于行波效应使地震峰值到达墩梁产生时间差，从而产生相对位移。考虑行波效应后墩梁和塔梁间相对位移变化不规律，震荡次数减少。可能是由于墩、塔和梁间结构特性不同导致振动周期不同，引起了非同向振动。

4 结论

基于非线性时程分析法对比了考虑行波效应的非一致激励与一致激励下大跨度结合梁斜拉桥的地震响应，得到以下结论：

1)桥梁结构基本周期为5.838 s，属于长周期柔性结构，第一阶振动为主梁纵飘，满足斜拉桥半漂浮体系的特征。

2)对于主梁与塔顶纵向位移，行波效应总体上使其地震响应减小。当波速为500 m/s时，非一致激励下主梁和塔顶纵向位移分别为一致激励下的75%,93%;随着波速的增大，位移变化平缓，逐渐趋于一致激励。

3)当波速较小时，考虑行波效应后塔底截面的弯矩及剪力总体上比一致激励要小，但是墩底截面的弯矩和剪力略微增大;当波速较大后，考虑行波效应的非一致激励与一致激励的地震响应基本相同。对于本文的大跨结合梁斜拉桥，考虑行波效应对于桥梁抗震有利。

4)考虑行波效应后墩梁和塔梁间相对位移均有所增大，墩梁和塔梁间相对位移变化不规律，震荡次数减少。