基于Radon变换与滤波反投影的CT模型及应用
2018-08-01何世宇
何世宇
(河海大学计算机与信息学院,南京 211100)
0 引言
CT(Computed Tomography)技术,也称计算机断层成像技术,是利用X射线对不同厚度物品穿透性与衰减性的不同,在不破坏待测品内部结构的情况下,根据物体周边所获取的某种物理量(如波速、X线光强、电子束强等)的投影数据,运用一定的数学方法,通过计算机处理,重建物体特定层面上的二维图像以及依据一系列上述二维图像构成三维图像的技术。
从1971年Hounsfielld发明头颅CT到20世纪80年代,CT技术的发展主要在于扫描部位的延伸,即从单一的头部检查拓展到体部检查。CT技术的发展大致分为以下四个阶段:第一代CT装置通过平行束旋转扫描获得投影数据;第二代使用小角度扇形射线束来代替平行束;第三代设备仅包含扇形束的旋转扫描动,不再采用平移动作;第四代设备将探测器固定在360°的圆周上,仅旋转X射线源以解决幻影伪像问题。由于被测物与扫描环境的复杂性,CT扫描方式日趋灵活。
由于CT技术的特点,使其广泛应用于医疗检查。除了医学领域,CT在物质探测方面同样具有的巨大的优势,尤其在工业、地球物理、工程、农业、安全检测等行业得到了广泛的应用。
1 基础理论
1.1 Radon变换
Radon变换是CT技术的主要理论基础,1917年由数学家Radon证明。Radon变换是一种积分变换,它的本质是对原来的函数做空间转换,将XY平面上的点映射到AB平面,原来XY平面上的某条直线的所有的点在AB平面上都位于同一点,即对物体进行线积分。根据AB平面上点的量化指标,可得XY平面在该条线上的部分特性。这便是Radon变换的实质。
假设有一条穿过空间中某物体的X射线,其方程为:

其中θ影响射线的斜率,ρ影响射线的位置。同时我们假设空间中该物体对射线能量的吸收强度可以表示成函数:f(x,y),那么物体在该条X射线上所吸收的能量可以表示为积分:
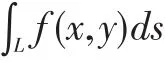
其中ds是该射线的微分。上述积分常借助Delta函数的抽样性进行化简求解,表示为:
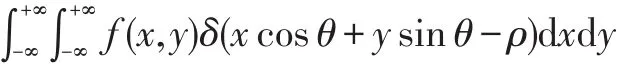
其离散近似可写为:
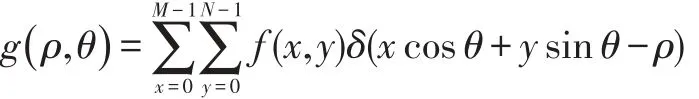
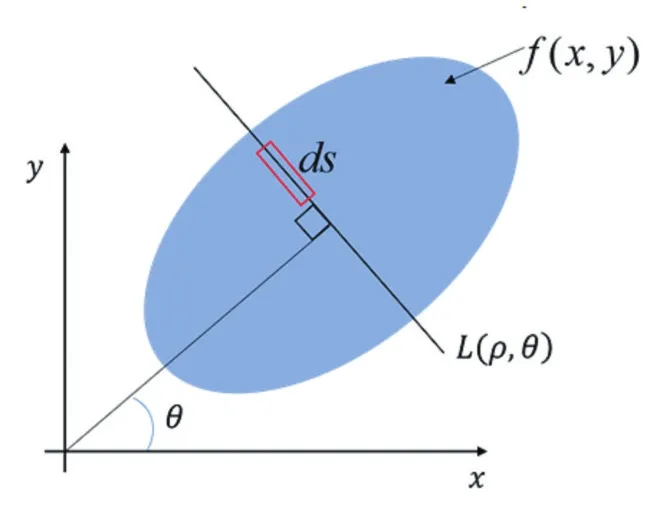
图1 物体在L的线积分
由此可见只要给定一组 ρ和θ,即可以得出一个沿L的积分值。因此,Radon变换就是函数 f(x,y)的线积分。
从一条射线推广到多条,假设有多条平行与L的线,它们有相同的θ,不同的 ρ,我们对每一条这样的平行线都做 f(x,y)的线积分,会产生很多投影线,如图2所示。也就是说对一幅图像在某一特定角度下的Ra⁃don变换会产生N个线积分值,而每一个线积分值会对应一个自己的位置ρ。各个角度的Radon变换值汇总在一起就构成一幅Radon变化图。
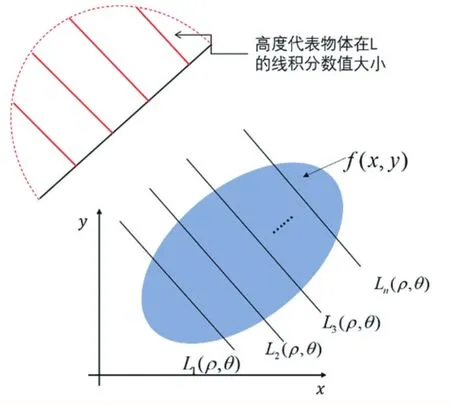
图2 物体在射线束下的投影
1.2 滤波反投影
滤波反投影(FBP)算法是在傅立叶中心切片理论基础上的一种算法。它在反投影前将每一个采集角度下的投影进行卷积处理,从而改善复原后函数的模糊现象,重建的图像质量较好。
根据傅立叶中心切片定理的定义可知,对投影的一维傅立叶变换等效于对原图像进行二维的傅立叶变换。有了该理论的支持,就能通过在投影上执行傅立叶变换,得到物体的的二维傅立叶变换。
由此,我们可以列出投影重建的步骤,在投影重建的过程中,先把线阵探测器上获得的投影(衰减后的射线能量)数据g(ρ ,θ)进行一次一维傅立叶变换得到G(w ,θ),再将 g(ρ ,θ)与滤波器函数H(w)进行卷积运算,得到各个方向卷积滤波后的投影数据g'(ρ ,θ);然后把它们沿各个方向进行反投影,即按原路径分配到每一矩阵单元上,进行重叠后得到每一矩阵单元的CT值;再经过适当处理后得到被扫描物体的断层图像。具体算法流程见图3。
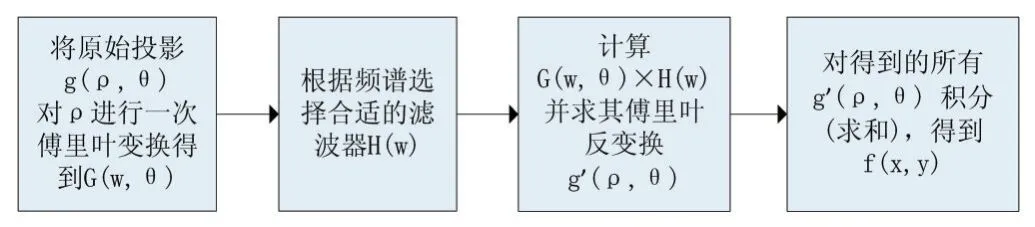
图3 FBP算法流程图
由此我们可以得到物体对射线能量吸收强度的表达式:

2 MATLAB函数
在 MATLAB中,有专门的radon()函数和 iradon()函数来实现Radon变换与滤波反变换的算法,下面将对这两个函数的用法以及应用效果进行简单的介绍。
2.1 radon函数
radon函数的常见用法有以下两种:
(1)R=radon(I,theta):若 theta为一个数值,R 值则是计算图像I在theta方向上的Radon变换;若theta为一个角度范围,那么R则为一个矩阵,表示在该范围内的Radon变,其一个维度代表角度(一般为0到180°),一个维度代表积分值。
(2)[R,xp]=radon(I,theta):R 的返回值含义同上,矩阵“xp”中包含了射线的位置信息,即ρ信息。
Shepp-Logan是测试CT系统的常用图片,我们使用它来演示radon函数的使用效果,图4为Shepp-Lo⁃gan测试模型。

图4 Shepp-Logan测试模型
output_size=2*floor(size(R,1)/(2*sqrt(2)))
我们对上一小节Radon变换产生的四个图像进行滤波反投影变换,得到如图6的四幅图片,可以看出随着旋转角度变小——也就是增大投影个数,图像重建越好,越接近实际效果。
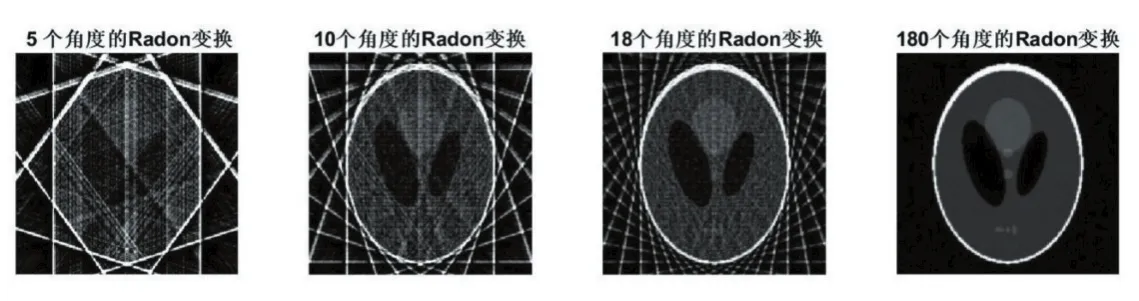
图6 不同投影个数的图形重建情况
下面我们通过在radon函数中设置不同范围的theta值,对图4进行Radon变换,我们将180°分别分为了5、10、18、180个角度,变换效果见图5。可以看投射的角度越多,产生的Radon变换越清晰。

图5 不同投影次数的Radon变换
2.2 iradon函数
iradon函数是MATLAB中提供的CT复原函数,其原理是使用滤波反变换对切片图像进行复原,用法如下:
I=iradon(R,theta,interp,filter,frequency_scaling,output_size)
其中R为反投影数据;theta为描述角度的变量,既可以是包含角度的矢量(给出每次旋转的度数)也可以提供一组行向量(如 0、1、2…178、179);interp 是字符串,定义了重建函数时选用的内插函数,默认使用“linear”线性插值;filter指定了滤波反投影时选择的滤波器,默认为“Ram-lak”滤波器,它可以恢复图像的频率成分,频率越高,恢复越多。frequency_scaling是处于(0,1)范围内的标量,通过改变频率轴的比例来修改滤波器,默认1,若小于1滤波器将被压缩。output_size是标量,规定了重建图像的行数和列数。默认值为:
3 实例分析
2017年全国大学生数学建模竞赛的A题即为CT图像复原,在这一节我们将对该题目的难点,即图像转动与缺失问题进行分析,并介绍如何使用MATLAB处理上述两类问题。
3.1 图像转动问题的解决
题目中给出了模型的形状及其吸收率,其中黑色部分吸收率为0,白色部分吸收率为1,我们对模板进行标准的Radon变换,模板及变换的结果见图7。此外题目还给出了该模板经过某一般条件下的Radon变换数据,如图8。
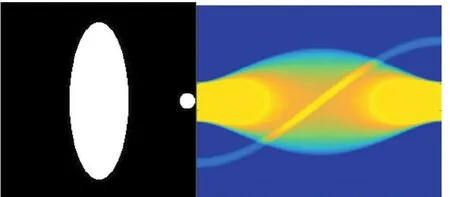
图7 模板及其Radon变换
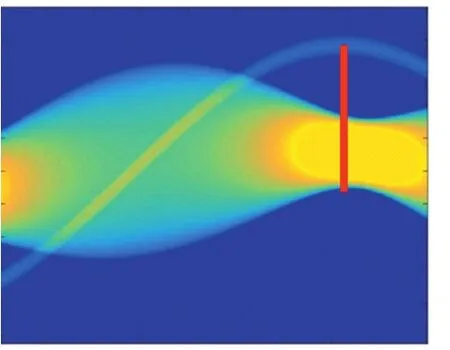
图8 某一般情况下的Radon变换
由图8可以得知,由于红线位置的图形宽度最窄,吸收的射线强度最弱。假设从模板正下方投影为0°,红线位置即为模板180°方向的射线束的线积分。因此我们得知该对模板Radon变换的初始角度非0度。经过等比例换算得知,Radon变换的初始角度约为30度。下面我们对原数据进行滤波反投影变换(见图9),左图为角度范围0°到180°,右图将角度进行修正,角度范围为 30°到 210°。

图9 不同角度范围的滤波反投影图像
可以发现右图相比作图位置得到更正,位置由未修正前的倾斜恢复到了模板形状,但是图像信息发生了损失,及丢失掉了右方圆的信息,下一小节将会讨论如何恢复未显示的信息。
3.2 图像缺失问题的解决
为了确定是数据丢失还是显示范围过小,我们对滤波反变换后的图像进行三维显示(图10),我们发现滤波反变换后的数据信息中已经包含了小圆的信息。
经过对模板与复原后图像的形状等参数的分析,我们发现由于模板的几何中心与旋转中心存在一定的位置偏移,使复原后的几何中心偏离范围。因此复原后的图片信息不能在模板范围内显示完全,需要比模板更大的范围才能显示完备的信息。经过对iradon函数的研究发现,其最后一个输入可选项output_size即为可控制图像大小的参量,我们通过对图形大小的扩展,即可复原出原图片显示丢失的内容。经过扩展后的图像见图11。
4 结语
计算机断层成像作为医学领域重要的技术之一具有很高的研究价值。若仅会使用MATLAB中的工具箱,对旋转角度与尺度变换等问题需要配置一些额外的参数才看可以很好的解决,因此对Radon变换与滤波反投影算法深入的学习是必不可少的。此外,旋转中心与几何中心位置的确定等问题,目前还需要针对具体问题进行逐一建模才可以解决,如何得到普遍性的模型还有待进一步的研究。
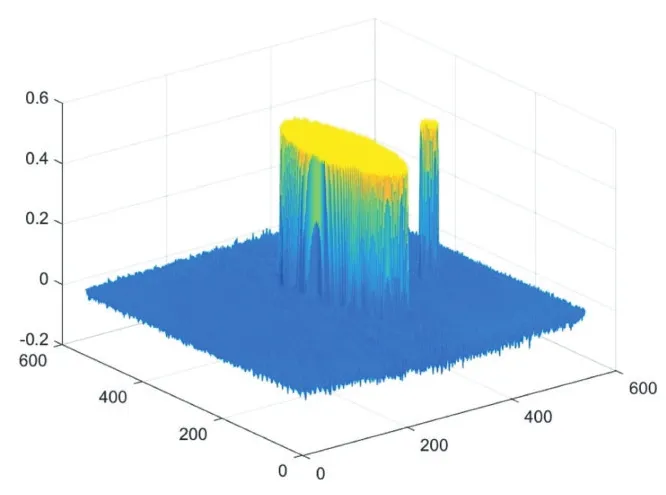
图10 滤波反变换结果的三维化

图11 扩展范围后的滤波反投影图像
