双基球扁药工艺优化仿真研究

王冬磊，张智禹，尹爱军

（1. 中国工程物理研究院 化工材料研究所，成都 621900；2. 重庆大学 机械工程学院，机械传动国家重点实验室，重庆 400044）

双基球扁药是一种具有高能量、高燃速、薄弧厚、燃烧性能好的球扁形发射药[1]。由于其成球过程涉及溶解、成球、预蒸、蒸溶等多个工序的工艺参数控制，而加工过程内在机理复杂，国内外在机理分析尚处于探索阶段，研究的理论基础薄弱，尚未形成成熟的成球工艺控制技术，导致成球直径、弧厚偏差大的问题[2-4]。大量研究表明，成球过程各工序温度及工序时长对成球质量影响尤为重要[5-7]，这些参数与成球质量之间有着复杂的相互关系，且成球过程是一个复杂的非线性过程。已有文献资料显示，对于成球工艺参数与成球质量间关系的研究还不够深入，以致无法从工艺机理角度给出合适工艺参数指导生产。

近年来，人工神经网络研究不断深入已使其成为人工智能领域的前沿技术，而BP神经网络由于其突出的非线性映射及自学习自适应能力在非线性建模、函数逼近、模式分类等方面广泛应用[8]。Tsai和Luo[9]运用BP神经网络在注塑工艺参数优化方面作了深入研究。刘荷花[10]采用BP神经网络优化了激光焊接工艺参数，达到了高精度、高质量的设计目标。BP神经网络的不断发展也为成球过程工艺优化提供了新的思路与方法。文中利用BP神经网络的非线性拟合能力，运用根据北化集团双基球扁药生产成球工艺过程产生的工艺仿真数据建立了工艺参数与成球质量参数间的关系，形成了神经网络算法模型。为今后双基球扁药生产提供优化的工艺参数，进而提高双基球扁药成球质量。

1 双基球扁药成球工艺原理

内溶法成球的工艺流程为：加料混合—升温—溶解—成球—预蒸溶剂—脱水—驱残溶剂—保温—冷却等9个工序[7]。整个过程在同一个成球器中顺序进行。

1）加料混合：将硝化棉、吸收药、中定剂、溶剂等原材料加入水中、搅拌。

2）升温：混合一定时间后，将成球器中的夹层升温，达到溶解温度。

3）溶解：升温后，保持温度一定时间，以进一步溶解原材料，最终原材料被溶解为具有一定黏度的高分子溶液。

4）成球：在成球器的搅拌作用下，高分子溶液以液滴的形式被分散到水中，这些液滴不与水相容，在液滴表面张力作用下，表面积有尽量缩小的趋势，以减小其表面能，最终小液滴成为球形。同时在成球器中加入固定配比的明胶，使其保持稳定且分散成颗粒状。

5）预蒸溶剂：升温将球中的溶剂蒸发一部分，以增大球的表观黏度，防止球变形。预蒸溶剂阶段蒸出溶剂总量的70%左右。

6）脱水：脱水阶段是控制药粒密度的重要操作，由于球中有一定量的水分，含有水分的球在驱除溶剂后收缩不良、松质多孔。为了脱水，在水中加入一定量的可溶性盐类，利用介质水中盐产生的渗透压作用，使球中的水分不断渗透到介质中。脱水截断温度要高，渗透压要大，这样有利于提高脱水速度，但在脱水阶段要防止溶剂过早蒸发，造成药面过早的收缩硬化，导致球内水分不能完全渗透出来，因此脱水阶段的温度低于恒沸点。

7）驱残溶剂：脱水结束后，开始升温，在高温的作用下，溶剂从球表面蒸发穿越水介质排出。此过程中为防止粘结，蒸溶的速度不宜过快。

8）保温：恒温一段时间，以尽可能蒸发出残余溶剂。经过恒温过程后，球中绝大部分溶剂被驱除，球粒逐渐硬化定型，形成密度较大、形状规则的球扁药。

9）冷却：保温一段时间后，降低成球器温度，出料洗涤，进行后续工序。

由上述成球工艺流程可以看出，成球工艺复杂且持续时间长。同时由于成球理论研究欠缺、控制模型不明确导致目前生产工艺参数调控主要依靠人工经验决定。文中为解决此问题，利用成球工艺过程仿真数据，结合BP（Back Propagation）神经网络强大的非线性拟合能力建立由每个工序持续时长及工序结束时温度值组成的共18个工艺参数与成球质量参数间的关系模型，对成球工艺进行优化。

2 BP神经网络

BP神经网络是一种前向型网络，采用误差反向传播算法进行训练[11]。它是目前应用最为广泛的一种神经网络模型，不需人工参与即可自动学习输入与输出之间的映射关系。其在解决非线性问题和复杂系统时具有其他算法模型无法比拟的优势，因此在学术研究和工程领域中广泛应用[12]。

2.1 BP神经网络的基本原理

BP神经网络结构如图2所示，由一个输入层、一个输出层和若干隐含层组成。在各层内部，神经元没有连接，层与层之间的神经元通过权值相互连接。给予输入层一组学习样本，其通过隐藏层神经元最终传播给输出层，输出层的值作为BP神经网络的输出。在误差反向传播过程中，由网络实际输出与期望输出之间误差的负梯度方向，从输出层向隐藏层再到输入层，逐层修正连接权值。前向传播与误差反向传播过程交替进行直至网络收敛。

式中：f1(x)与f2(x)分别为隐藏层与输出层的激活函数。通常隐藏层的激活函数为 Sigmoid函数，即f1(x)=1/(1+e-x)；输出层的激活函数为 Purelin函数,即f1(x)=x。

2.2 BP神经网络的设计

根据Kolmogorov定理[13]可知，任意函数均可由一个3层BP神经网络逼近，因此文中采用3层BP网络结构。将成球阶段各工序持续时长及工序结束时的温度值共18个参数作为输入层参数，输出层参数由成球直径、弧厚2个参数组成。隐藏层节点数p由经验公式（3）确定：

式中：p为隐含层节点数；m，n为输入层、输出层节点数；c为 0到 10之间的整数。经过尝试最终取隐藏层节点数为9。

网络隐藏层激活函数选择 Relu函数，输出层激活函数为 Purelin函数。同时选择均方误差（MSE）作为BP神经网络性能评价指标，其计算公式为：

式中：q为样本个数；yi为网络输出样本值；oi为实际样本值。

BP神经网络参数见表1。

表1 BP神经网络参数

2.3 BP神经网络训练

根据北化集团生产双基球扁药的成球工艺过程，产生50条工艺仿真数据，将其中40条用于模型训练，剩余10条数据用于检测所建立的 BP神经网络的泛化能力。训练结果如图3所示，当训练次数达到2000次以上时，训练均方误差已为 0.007，而且训练次数越大，训练均方误差越小；当训练次数达到7000次以上时，输出误差稳定在0.001附近。

3 成球工艺参数优化

第2节得到了训练好的BP神经网络，为验证训练好的BP神经网络是否学习到工艺参数与成球质量的内在关系，将余下的10条数据中工艺参数作为输入，比较BP神经网络的输出值与仿真值。图4给出了成球直径的BP神经网络输出值与仿真值的比较，可以看出，成球直径对应的BP神经网络输出值曲线与仿真值曲线基本重合。图5给出了成球弧厚的BP神经网络输出值与仿真值的比较，可以看出，成球弧厚对应的BP神经网络输出值曲线与仿真值曲线也基本重合。说明它已基本掌握了成球工艺仿真数据的内在关系。

表2列举了前5条成球质量数据的预测误差率。成球直径的平均误差率为1.27%，成球弧厚的平均误差率为2.08%，表明训练后的BP神经网络可以用于工艺优化。通过尝试不同工艺参数，用此模型输出成球质量参数与生产要求质量参数对比，从而得到符合要求的生产工艺参数。因此，可以认为将此工艺参数作为实际生产中的工艺控制参数时，可得到理想的成球质量。

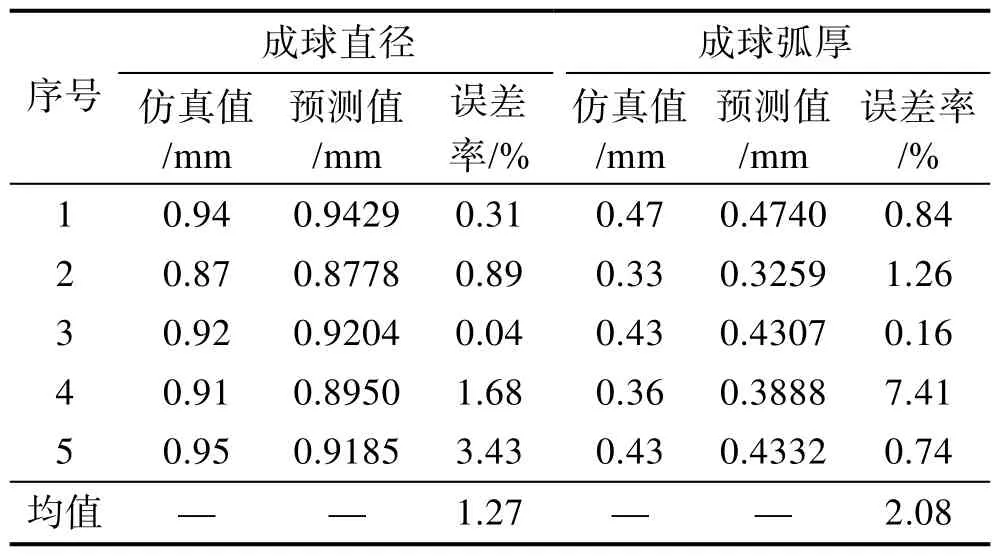
表2 质量数据预测误差率

4 结论

1）将 BP神经网络用于化工方面，解决了在理论不清的情况下如何优化生产工艺的问题，建立了双基球扁药成球工艺参数与成球质量参数之间的复杂关系模型。测试样本预测结果表明，BP神经网络的输出与仿真值之间误差在 3%以内，因此可用于优化工艺参数。

2）运用此模型可省去生产试制，减少试制带来的人力、物力和财力的损耗，提高生产效率，具有较好的应用前景。

3）在进行实际的双基球扁药生产时，工人只需根据成球尺寸要求，给出成球弧厚，直径的数值，通过该方法即可快速地找出满足要求的工艺参数组合（各环节工艺温度、时间）用于指导生产，这样既提高了参数设计的效率又大大地减少了对工人的技术要求。