MIMO-OFDM系统中检测器复杂度与性能分析∗

周 玲 李湘文 张 双 杨健云

（1.成都理工大学工程技术学院 乐山 614000）（2.新桥镇贯底中学 衡阳 421300）

1 引言

通信系统中，不断提高数据传输速率需要消耗大的带宽。正交频分复用（OFDM）能大大降低接收机的复杂度［1］，而多输入多输出（MIMO）信道提供了更大的容量和更高的可靠性。MIMO与OFDM相结合的编码系统可在获得多样性增益同时获得额外的性能改进［4］。

为了充分发挥这种容量增加的优势，需要开发高效可靠的接收机来成功地应用这种MIMO技术。一般来说，在多用户检测的情况下，接收机被分为三种类型，即最大似然（ML）检测器、线性检测器和连续干扰抵消检测器［6］。然而，近年来，其他替代方法如球面解码和信道截断法等已被开发和研究出来。球体探测器（SD）采用QR分解（正交三角分解法），有效地将信道三角化，采用这种信道结构，并利用一种树搜索方式来减小搜索空间，以便降低复杂性提高性能［9］。球面解码算法可分为两类：深度优先搜索和广度优先搜索算法。k-best LSD算法（KLSD）是一种具有固定复杂度的广度优先搜索算法［10］。近年来，又提出了一种信道截断方法，与球面解码类似，它也是一个两级探测器。该方案还可以通过选择适当的聚对角化顺序，在复杂性和性能之间进行折中选取［11］。

2 系统模型

基于OFDM的MIMO传输系统中，用NT表示发射天线、NR表示接收天线，NSC表示子载波，采用正交幅度调制（QAM）［12］，A 的大小为 | A|=2Ω，Ω表示比特/符号数。我们用NT×1表示第(k)个子载波的符号向量为

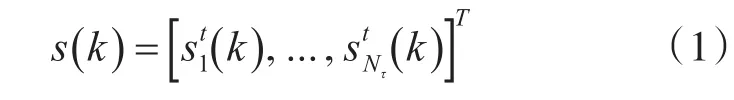
接收矢量y(k)用离散傅立叶变换（DFT）和长度为NR的噪声矢量n(k)进行解调后得出，去除循环前缀（CP）后 y(k)可以表示如下：

在DFT变换中，接收天线NR的副载波NSC的加性噪声为n(k)。假设n(k)是均值为零，方差为的加性高斯白噪声。MIMO信道的频率响应可以用NSC的复杂信道矩阵描述如下：

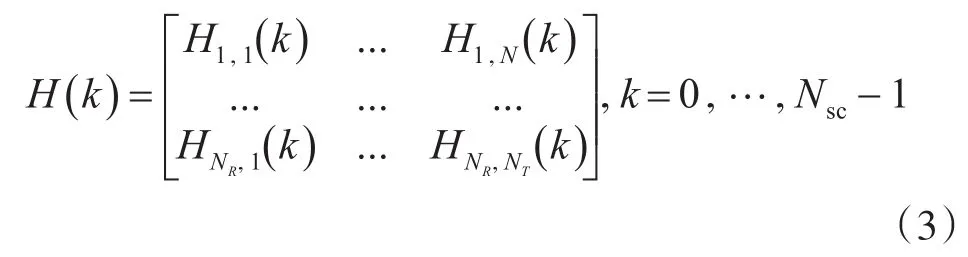
由上可见，该矩阵的大小为NR×NR。

3 KLSD探测器和ASY-PD探测器

3.1 KLSD探测器

该算法利用所谓的QR分解将信道转换为三角形，然后利用一种简化的树搜索方式来确定软决策值［13］。QR分解可以在ZF中进行，也可以在MMSE中进行。ZF可以直接进行QR分解，比如，可将信道分解为H=QR，其中Q是一个酉矩阵，R是一个三角形矩阵。通过将y乘以QH，可以有效地将信道转换为三角形信道，方便进行树搜索。在ZF均衡器中，QR分解的一个缺点是噪声的增加，尤其对于高层来说增加的更加明显。在MMSE相比较于ZF的QR分解具有更好的性能。由扩展信道矩阵H和扩展的接收向量y，定义如下：

其中Q为(NT+NR)×NT的正交矩阵，R为NT×NT的上三角矩阵。用y乘以QH得出：

对于后树搜索算法，本文中考虑了列表球算法（kLSD算法），对仿真过程描述如下：用表示 S矢量的最后NT-i+1元素，并定义第i层的部分欧氏距离的平方（PED）为

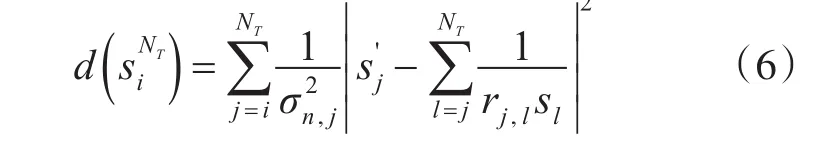
其中rj，l为上三角矩阵 R的( )j，l元素。该算法在平方PED基础上，在每一层找到固定的符号K，并将其进一步存储在树搜索步骤中。一旦完成树搜索，就给出每个比特的LLR值，称为第m比特，如下式所示：

在简化的k-best树搜索下式（7）的一个问题是，当没有可选符号，也就是第m比特为0或1时，对数似然比（LLR）将无法获得。

3.2 ASY-PD探测器

该探测器类似于连接信道的缩短均衡器和最大似然序列估计器［14］，是为了高斯ISI信道而开发的。可将聚对角化看作是结构化信道的缩短/截断，其主要思想是为了减少噪声的增加而部分地进行干扰［15］。一旦信道被转换成多对角线后，就可利用底层信道的多对角线结构来进行网格解码。在线性检波器和球面解码中，聚对角化也可以在ZF或MMSE检测算法中执行。

BL是一个NR×NT的L阶聚对角化矩阵，对任意对角矩阵 Dl来说 ，L=0，…，L-1，MIMO信道有效的聚对角化，也就是说：

其中有效信道是由移位对角矩阵的和表示的。比如聚对角化形式。BL矩阵的每一列，bL，k，都可以通过将信道矩阵划分为三种术语来得到；期望的信号hk，不被考虑的信号HL，k和无效或抑制干扰HˉL，K。 PD-ZF的 BL，K如下式所示：

不对称公式：

由下式给出

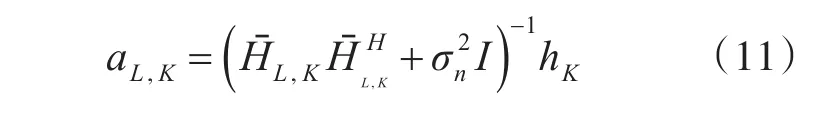
不对称公式：

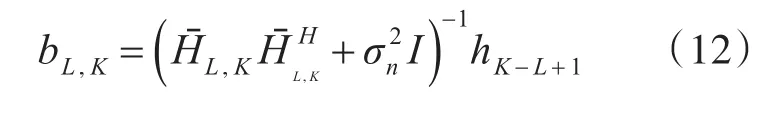
4 仿真结果

4.1 复杂性

几个算术运算的计算复杂度归纳总结在表1中。a指实数加法，m指实数乘法。复数乘法/除法需要3个触发器，而复数加法需要1个触发器。

表1 算术运算的计算复杂度

4.2 性能

在频率选择性衰落信道中，对MIMO-OFDM编码进行了链路级仿真。对于信道模型，假设每个路径（天线TX到RX天线之间）都有不相关的频率选择性衰落与功率谱：[0，-3，-6，-9，-12（]dB）以及延迟样本：[0 ，1，2，3，4] 。

比较KLSD的误码性能和6×6天线配置的ASY-PD，4QAM调制和羞分编码速率如图1所示。在KLSD中，ZF和MMSE预处理器的性能差异在4QAM中是明显的，而ZF和MMSE预处理器之间的差距会随着给定的候选调制尺寸的大小而降低，并且随着变量K的增加，性能也得到了提高。非对称PD表现出相似的趋势，即在ZF和MMSE中，PD和MMSE对4QAM有明显的区别，除了L=5的时候，随着变量L的增加，性能得到了更好的提升。这一趋势与分析结果相一致。

图1 对KLSD和ASY-PD BER性能比较

4.3 权衡性能

表2和图2显示在使用6×6天线配置，4QAM调制方式和不同编码速率下探测器的权衡性能。

表2 权衡性能(6×6，4QAM)

由表2和图2可知，在误码率BER为0.0001，触发器分别为KLSD和非对称PD的信噪比[d B ]。KLSD的性能优于PD，其码率高（即：R=2/3），而在较低复杂度的情况下，ASY-PD较KLSD更适合于低码率（即：R=1/2）使用。

图2 信噪比与复杂度之间的权衡(6×6，4QAM)

5 结语

本文介绍了MIMO-OFDM系统中，两种检测器算法比较，即KLSD、非对称聚对角化探测器的ZF和MMSE检测算法，以及在编码传输和频率选择性衰落信道中，ASY-PD使用咬尾结构的网格探测器算法。综合比较后，我们发现在编码速率方面，前者的性能优于后者；后者的复杂性随着编码速率的越少而降低优于前者。这两种算法有效地解决了复杂性和性能之间的问题，而检测方案的选择又可以基于硬件实现的简易性等。