基于通视性分析的UUV目标测试航路快速规划方法研究∗

李金亮

（中国人民解放军91404部队93分队 秦皇岛 066001）

1 引言

水下无人航行器（UUV）是不需要由处于潜水器内的人员来操控的水下运载体［1］，它作为一种海上舰艇的辅助作战武器有着广泛而重要的军事用途，如收集情报、对敌方军情进行监视和侦查等［2］，美国海军已配备了第一代潜射水下无人航行器，可以到达人类难以抵达的地方进行收集情报、攻击目标等活动。此外在民用方面，水下无人航行器对人类有效开发海洋资源起到关键作用，如搜集海底高程，洋流气象等环境数据、协助石油与天然气开发、海底生物科学研究等等，不仅可以改善效能还能降低费用。因此，近年来水下无人航行器的研究受到各国越来越多的重视，现已成为各发达国家军事海洋技术研究的前沿［3］。

2 水下航路规划问题概述

航路规划是综合考虑威胁、地形、航行器性能和任务需求等多种因素，找到从发射点到目的地的最优航路，并要求生存概率最大和航行时间最短［4～5］。在水下无人航行器航路规划过程中，通常需要考虑的影响因素有：航行器自身的物理性能、海洋的气象条件、海洋的水文地理环境、战场环境态势和我方的战略战术要求等。它是一个综合性很强，复杂程度很高的问题，本文简要概括出四个主要需要考虑的要素，如表1所示。

表1 主要因素

3 复杂海洋环境水下规划空间建模

在水下无人航行器航路规划中，复杂海洋的环境我们可以看作是各种各样的约束区域［6］，如岛屿，陆地，敌方监视区等等，因此我们需要对其进行建模。

1）限制区

限制区是指航行器航行时不能通过的区域，如岛屿、陆地、暗礁、禁航区等。如图1所示，限制区用一个多边形柱状区域来表示，航路规划时，规划路径不能从这个多边形区域通过，当航路通过该区域的代价为无穷大，因此航路需要从限制区周围绕过限制区。

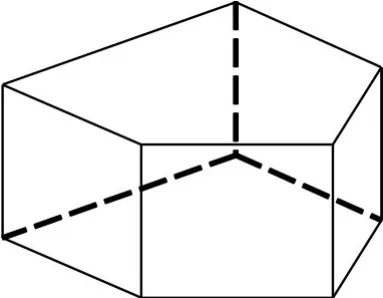
图1 限制区模型

2）威胁区

在真实的战场环境下，敌方往往会在海洋中部署大量兵力（如军舰、潜艇等），会对航行器的航行安全造成威胁，敌方兵力往往先会用声呐探测我方航行器的存在，然后再发动攻击，而声呐的探测目标的范围通常为一个椭球形的区域，因此用一个椭球来表示威胁区，航行器进入该区域时，有一定概率被威胁区摧毁。如图2所示威胁区的作用区域为

其中，Sth是威胁区的作用域；(x0，o，y0) 是圆柱体底面的圆心坐标；a，b是椭球体的赤道半径（沿着x和y轴），c是极半径（沿着z轴）。

图2 半椭球体模型

航行器经过威胁区的代价为经过椭球区域的时间再乘以威胁系数，公式如下：

其中 f代表经过威胁区的代价，l代表航行器经过威胁区的长度，vu代表航行器的航行速度，α代表敌方兵力威胁的威胁系数，根据威胁区威胁程度的不同，将威胁区分为九个等级，每个等级的威胁系数不同，等级越高，威胁系数就越大。

3）必达区

在完成战术、战略任务时，可能会指定航行器经过某片区域以完成特定的任务，这时航行路径必须要经过的该区域，这个区域就是必达区，它的模型用多边形柱状来表示。此外还有海流区、匹配区、风浪区等模型就不依次列举了。

4 基于通视性分析的快速航路规划方法

4.1 通视性概念与模型

通视性分析本质上就是判断观测点与目标点之间的视线是否通达［7～8］，转化到规划空间中，就是判断连接该两点的视线是否与海洋环境中的各种约束区域相交，这个判断过程叫通视性检查，也就是线段与多边形、圆、椭圆的碰撞检测过程。给定矢量规划空间中的约束区域集合C和两个点P1、P2，对于任何一个约束区域 x(x∈C)，如果都有φ(lP1P2，x)=0 ，那么P1、P2可通视的，其中 lP1P2代表直线段P1P2，函数 y=φ(l ， x)是计算直线段l是否与约束区域x相交，这个函数的取值只可能是0和1，若取值为0则直线段l与约束区域x没有相交，否则则表示直线段l与约束区域x相交。即规划空间中任意两点P1、P2可通视的条件是∀x，x∈C，都有φ( )lP1P2，x =0。

如图3所示，在规划空间中，目标点A、B与观测O点是否通视，主要判断线段OA、OB是否与规划空间中的约束区域相交，从图中可以知道线段OA与约束区域C相交了，因此O、A两点不能通视，而线段OB与所有约束区域都没有相交，因此O、B两点是通视的。

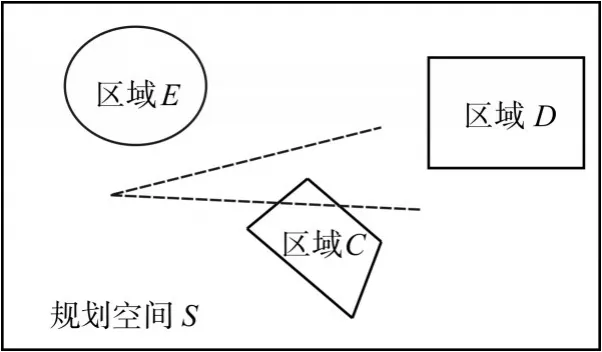
图3 点通视性示意图

通视性问题按照输出信息的维数可以分为点通视性、线通视性和区域通视性问题，但是在航路规划中主要研究的是两点之间的通视性算法问题。

4.2 基于通视性分析的快速航路规划

基于通视性分析的快速航路规划的主要策略就是先对航行器航行的起点和目标点进行通视性检查，若这两点可以通视，则可以从起点直线到达目标点，否则两点之间不能通视，则选择离航行器当前位置最近的环境约束区域进行通视性处理，不同类型的环境约束区域通视性处理方法也不尽相同，按照通视性处理后的路径前进，比如限制区就是按照绕过限制区的最短切线路径前进，到达下一观测点再进行通视性检查，处理，前进，然后循环往复，直到最终到达目标点。这里的观测点指的是刚绕过（或通过）环境约束区域的节点，例如绕过限制区的下一个观测点就是目标点与该限制区的切点，通过海流区的下一个观测点就是航路穿过海流区的交点。

以图4为例来进行说明。从起点S开始进行航路规划，先对起点S和目标点T进行通视性检查，发现直线路径上存在限制区A，这两点不能通视，因此对限制区A进行通视性处理，求取绕过限制区A的最短切线路径，然后沿着切线前进，直到下一观测点，下一观测点为切点N，再对观测点N和目标点T进行通视性检测，发现直线路径上还存在海流区B，因此在对海流区进行通视性处理，求取通过海流区的路径，图中求取出的路径为直线通过海流区的路径NT，因此沿着路径NT前进，到达下一观测点，下一个观测点为交点J，再对观测点J和目标点T进行通视性检查，发现这两点可以通视，因此，可以直线到达目标点。这样通过多次对航行器的当前位置与目标点进行通视性检查，处理，前进，可以快速规划出比较满意的航路SMNT。

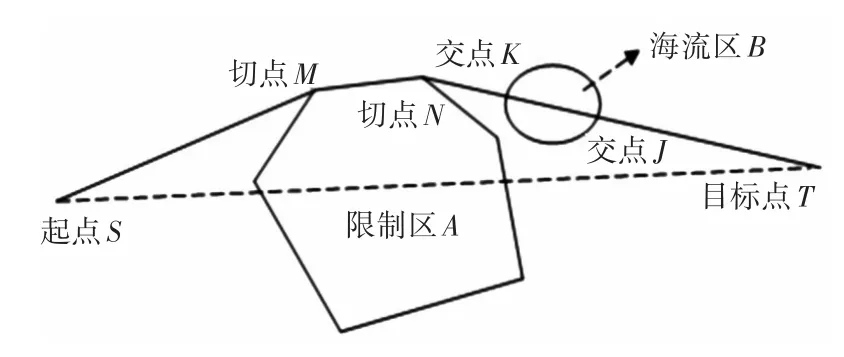
图4 基于通视性分析的快速航路规划示意图

基于通视性分析的快速航路规划方法流程：

Step1：生成引导点P；

Step2：设起始点S为当前点，引导点为临时目标点；

Step3：对当前点S和临时目标点P之间进行通视性检查；

Step4：若S和P能够通视，则判断P是否为最终目标点T，若是则得到最终航路，算法结束；否则将P设为当前点，切换下一个引导点为临时目标点，重复Step3，直到得到最终航路；

Step5：若S和P不能够通视，则选择离当前点最近的环境约束区域进行通视性处理，获取绕过（或穿过）该区域的路径，并将绕过（或穿过）环境约束区域的切点（或交点）设为当前点，重复Step3，直到得到最终航路。

基于通视性分析的快速航路规划方法的优点是规划速度很快，针对非常广阔的海洋环境非常适用，在通常情况下仅通过几次通视性检查处理，就可以迅速规划出一条满足约束条件的较优航路。

5 实验与仿真

本实验所用的规划地图为矢量电子海图，地图的范围为东经116.2°～东经132.5°，北纬21.5°～北纬41.2°，约为1793×2167km2的矩形地理区域。航行器考虑的环境约束区域包括必达区、海流区、威胁区、风浪区和限制区。本文进行两种类型的实验：第一类是简单环境下航路规划实验，简单环境中从航路起点到终点的路径上只存在少量的约束区域，主要是为了展示经过各种约束区域的规划结果，第二类是复杂环境下航路规划实验，航路起点到终点之间的路径上存在多个各种类型的约束区域。上述实验任务都采用传统 A*规划算法［9～10］和基于通视性分析的规划方法来进行实验对比分析，以下为部分实验结果。

图5 基于通视性分析的航路规划方法

表2 实验任务的航程和规划耗时

由实验结果可以看出对于广阔的海洋环境而言，无论海洋环境约束区域简单或是复杂，基于通视性分析的航路规划方法快速地规划出比较满意的航路。在简单环境下，基于通视性分析的规划方法与传统A*算法规划得到的结果相差不大，但是速度优于后者；而在很复杂的环境下，基于通视性分析的规划方法明显规划耗时小，规划速度快，但后者规划出的航路距离短一些，航路更优一些。因此基于通视性分析的航路规划方法规划速度快，但航路的最优性打了折扣，适合于对速度要求较高但航路最优性要求不是太高的情况。

6 结语

本文首先对水下无人航行器航路规划问题进行了简单概述，然后对复杂的海洋环境水下规划空间进行了建模，最后在该规划空间下研究了基于通视性分析的快速航路规划方法，给出了该方法的流程步骤，经过实验与仿真得出结论。针对复杂广阔的航洋环境，基于通视性分析的航路规划方法能够快速地规划出满足约束条件的较优航路，且较传统A*规划算法速度优势明显，给任务要求对速度要求较高但航路最优性要求不高的情况，如实时规划［11～12］，快速规划等，提供了一种有效地解决方法。