一类非线性反应扩散方程的周期解与沙漠植被周期现象

李春利

(商丘学院计算机工程学院，河南 商丘 476000)

0 引言

在自然界中，生物种群对共有资源的争夺多年来一直被认为是种群动态的基本过程之一。研究结果显示，如果一个自然环境中有两个或两个以上种群生存，那么它们之间就要存在着或是相互竞争，或是相互依存，或是弱肉强食(食饵与捕食者)的关系。当两个种群为了争夺有限的同一食物来源和生活空间而进行生存竞争时，最常见的结局是，能够在较少资源条件下生存的种群往往会战胜并取代另外一个种群。N个种群也是可以共存的，只要有N种不同资源的存在并且每个种群要保持对某种资源很强劲的竞争力，也就是说，它们都要有一个生态位(生态系统中每种生物生存所必需的生境最小阈值)。

在国际上，干旱和半干旱气候带的植被格局一直都是人们研究复杂系统中自发对称性破缺现象的典型课题。对有限水资源的争夺是该地区灌木类植被形成空间格局的主导因素，同时对水资源的争夺也会大大减少灌木类植物之间的相互影响。调查表明，在水量供应不足的情况之下，植被群是会灭绝的。

如果资源涉及空间动态的话，情况将变得复杂得多。当前理论和实践方面的研究多是种群对水源的竞争，然而光照及有限的其他资源也在逐渐被上层的水生浮游植物所消耗。这种模式或许可以拓展到动物群的空间动态，但不支持时间独立的模式。

对于单物种(灌木类)—单资源(水)系统的植被格局来说，实地研究揭示了大量稳定及近乎稳定的自发性分离模式。理解这种格局种群数量的潜在机制及其可观测到的恢复力是人们理解沙漠化进程很重要的一步，当然环境效应如气候变化和过度放牧都会破坏生态平衡而产生稳定的干旱状态。从技术层面上讲，水—物种体系被认为是一个空间扩展性非线性体系，也就是说，在某种参数范围内，会产生带状、点状或迷宫式的区域，以及其他由于正的反馈机制而产生的有序排列，比如对水径流和植物群蒸发的抑制作用。

总之，在种群所依托的单资源(比如沙漠地区的水资源)相对匮乏的情况下，要充分利用现代科学技术与生态系统的自然规律，搞好生态建设，尤其是植被建设，可谓意义重大。植被建设是生态建设的主体，水资源又是限制植被建设的主要因素，因此，研究植被格局与水资源的关系，探讨二者相互作用的机理具有重要的理论意义和实践意义。

文献[1]给出了描述沙漠地区植被分布与生长状态的无量纲化的非线性反应扩散方程模型：

(1)

式中：B(x，t)与W(x，t)分别表示t时刻x处的沙漠地区植被密度与水量密度；R(t)与V(x)分别表示t时刻的降雨量水平与x处的地形坡度向量；μ，λ与D均为正常数，依次表示植被在缺水条件下的相对死亡率，植被消耗水的程度与水的扩散作用系数；DΔW(x，t)+V(x)▽W(x，t)，W(x，t)B(x，t)，-λW(x，t)B(x，t)，分别反映径向水流反应扩散作用，供水量对植被的促进作用及植被对水的消耗作用。依据问题背景的实际意义，初始函数B0(x)≥0，W0(x)≥0。

为方便起见，假定在任意时刻方程组(1)在所研究的空间区域Ω上均服从空间周期边界条件，并假定B0(x)与W0(x)均为光滑函数，这里定义：

K=max{M，R0}。

(2)

1 解的存在性

定理1 偏微分方程组(1)存在唯一全局光滑解(B(x，t)，W(x，t))，并满足∀t>0，x∈Ω时，都有

0≤B(x，t)≤B0e(K-μ)t，0≤W(x，t)≤K。

(3)

证明由半群理论[2]可知，偏微分方程组(1)存在唯一一个以t=0为起点的局部解，为说明解是全局的，只需说明该解不会在其存在区间上发生爆破现象即可，如此则仅需式(3)成立，然后利用数学延拓的方法，方程组(1)存在唯一全局光滑解的结论自然成立。

由方程组(1)中第一个方程可知

(4)

方程组(1)中第二个方程可写成

(5)

下面利用反证法证明

W(x，t)≥0，∀t>0，x∈Ω。

(6)

假设存在一点(x0，t0)，使得W(x0，t0)<0，不失一般性，不妨设W(x，t0)在x0处达到极小值，且Wt(x0，t0)<0，则有(ΔW)(x0，t0)≥0，(▽W)(x0，t0)=0，将其代入式(5)，得到矛盾，因此式(6)成立。

下面做一个平移变换，同理可证

W(x，t)≤K，∀t>0，x∈Ω。

(7)

令u(x，t)=W(x，t)-K，则由式(5)可知

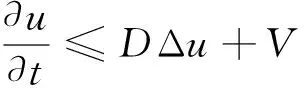
(8)

由式(2)即知u(x，0)=W0(x)-K≤0。

若存在一点(x0，t0)，使得u(x0，t0)>0，不失一般性，同样不妨设u(x，t0)在x0处达到极大值，且ut(x0，t0)>0，因此有(Δu)(x0，t0)≤0，(▽u)(x0，t0)=0，将其代入式(8)，得到矛盾，因此式(7)成立。

综上可知，式(3)成立。

2 解的周期性

不难发现，依据现有的偏微分理论很难直接分析出偏微分方程组(1)解的相关性质，这里我们根据生物学理论及相关背景知识[1]，可以考虑合理的简化模型——常微分方程组(见式(9))。事实上，我们完全可以假定B(x，t)与W(x，t)均服从均匀分布，这就使得它们独立于空间坐标x，或者就把B(x，t)视为Ω上的平均植被量或植被总量，记为B(t)，把W(x，t)视为Ω上的平均水量或总水量，记为W(t)。

根据文献[1]，在生物学意义上，偏微分方程组(1)可简化为常微分方程组

(9)

当然，对于初始点而言，只有非平凡情况B0>0，W0≥0才具有现实意义。

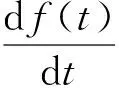
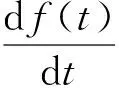
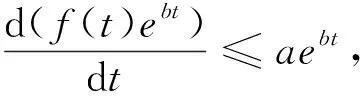
引理2 (Brouwer不动点定理)[3]设A为n维欧式空间R2中的紧致凸子集，则对A上的任一自映射f:A→A至少有一个不动点，即存在x∈A，使得f(x)=x。

该引理具体证明详见文献[3]。

定理2 若雨量水平函数R(t)为非负非平凡周期函数，即∀t>0，R(t)=R(t+T)，其中T>0为常数，则常微分方程组(9)总存在一个以T为周期的周期解。

证明对常微分方程组(9)中的两个方程关于t同时在区间[0，T]上积分，可得

由常微分方程组解对初值的连续依赖性，易知映射(B(T)，W(T))=F(B0，W0)，B0≥0，W0≥0是连续的。

为证明方程组(9)的周期解的存在性，只需证明映射F在R2第一象限(含边界)有一个不动点，为此，由Brouwer不动点定理可知，这里只需说明连续映射F把R2第一象限(含边界)的某个紧致凸子集映到自身即可。

这里设置二维平面(R2)上一个集合

SL={(p，q)|p≥0，q≥0，λp+q≤L}，易知，∀L>0，SL均为R2中的紧致凸子集。

由方程组(9)可知

其中，σ=min{μ，1}，从而由引理1可知

(10)

设定L满足R0≤σL，则由式(11)即知λB(t)+W(t)≤L，也即F(B0，W0)∈SL，因此由引理2可知，映射F在集合SL上存在不动点，此即证明了常微分方程组(9)以T为周期的周期解的存在性。

3 结果分析

定理1与定理2充分揭示了沙漠植被密度周期性现象的存在性。具体地说，若映射F的不动点在(0，q0)处取得(q0≥0)，由式(4)易知B(t)≡0，∀t≥t0，其中t0满足B(t0)=0，W(t0)=q0，此时方程的解表示稳定的沙漠状态；若不动点在(p0，q0)处取得(p0>0，q0≥0)，方程的解则反映了一种稳定的沙漠植被密度周期性现象，事实上，由式(4)可知B(t)>0，∀t≥t0，其中t0满足B(t0)=p0，W(t0)=q0，定理2又说明了B(t)是周期函数，因此B(t)总有正下界，也就是说，总是存在着稳定的沙漠植被密度周期性状态。