破冰船冰阻力估算方法研究

2018-07-31于晨芳吕烈彪柳卫东

船舶标准化工程师 2018年4期

于晨芳，吕烈彪，柳卫东

（江南造船（集团）有限责任公司，上海 201913）

0 引言

随着全球变暖，极地冰层逐年融化，使极地航线的开通成为可能。北极航线的畅通可以大幅缩短航程，大大推动了带有破冰能力船舶的研发。并且，北极地区蕴藏着丰富的油气及矿产资源，资源的开采及运输需要破冰船的支撑。除此之外，极地冰区的科学考察、资源勘探也需要依靠破冰船开辟航道，种种原因均使得破冰船需求增大。初步估计，这种需求在相当长的一段时期内还会有增大的趋势。然而，我国关于破冰船的研究开展较晚，对于破冰船的设计仍不具优势，尤其是对于冰阻力的研究，还没有标准可靠的预报方法，然而冰阻力的预报对设计初期船舶选型具有重要的指导意义，因此如何快速而准确的获得冰阻力成为当前时期迫切需要解决的问题。

国内外现存的关于冰阻力的预报方法主要有实船测试法、模型试验法、数值仿真法及经验公式法。实船测试法，主要是对实船进行试验，可测量到准确的冰阻力值并且可直接观测冰层破坏模式，但是试验成本很高[1]。模型试验法也是一种较为准确的冰阻力预报方法，能够最大程度重现船舶在冰区航行时的状态，是一种非常有效的冰阻力研究手段，但由于其也存在成本高、准备时间长的劣势，并不适用于初步设计阶段，并且目前冰阻力模型试验中冰材料的制作技术还有待进一步提升[2]。数值仿真法是近来发展较快的一种技术，成本低，耗时少，数值仿真技术能够对船体和冰层形状进行细致的描绘，并考虑到流体动力学作用对冰阻力的影响，但就目前而言，数值仿真中建立的冰材料模型的准确性还需要进一步验证，数值仿真结果的准确性还有待提高[1]。经验公式法是依据大量的实船测试结果及模型试验结果，总结归纳出的一种粗略的阻力估算方法。相较于其他3种方法而言，经验公式使用方便、简单，且在一定范围内具有一定的准确性，可以实现冰阻力的快速预报，进而指导破冰船的初始设计。经验公式法发展至今已有多种方法，其中，Lewis&Edwards公式[3]、改进的Lewis公式[4]、改进的Edwards公式[5]形式类似，公式中仅考虑了船宽、冰厚及航速的影响，考虑的参数较少。后来继续发展起来的还有Lindqvist公式[6]、Keinonen公式，这两者不仅考虑了船体几何参数，还考虑了冰属性参数对冰阻力的影响，更全面更准确地对冰阻进行预报。然而因为冰属性参数难以获得，对其广泛使用也产生了一定的限制。Riska公式[7]则舍弃了冰参数的影响，将冰阻力与冰厚、航速及船体几何尺度之间建立了更加紧密的联系，据实船验证，对阻力的估算有一定的准确性。

本文主要介绍利用Lindqvist公式及Riska公式（这2种方法实船验证准确性较好）来估算冰阻力的方法，其中包括冰参数的获得方法，在此基础上，以江南造船（集团）公司承建的某型极地破冰船为例进行冰阻力计算，并辅助以模型试验加以验证。对两组公式在冰阻力估算的准确性及公式适用范围给出建议，对影响冰阻力的船体几何参数进行了分析，研究结果为后续工程人员使用或其他研究者开展研究提供参考。

1 术语

L为船长，m；B为船宽，m；T为吃水，m；Lbow为船体首部长度，m；Lpar为平行中体长度，m；Lstern为船体尾部长度，m；ϕ为艏部倾角（艏柱处），(°)；α为水线进水角（Β/4处），(°)；Ψ为外飘角，，(°)；ϕ2为艏部倾角（Β/4处），(°)；v为航速，m/s；hi为冰厚，m；ρw为海水密度，kg/m3；ρi为海冰密度，kg/m3；σf为弯曲强度，Pa；μ为摩擦系数；ν为泊松比；Ε为弹性模量，Pa。

2 破冰方式及冰阻力估算方法

2.1 船体破冰方式及冰阻力分解

船体破冰方式可以分为2种：连续破冰和反复突进式破冰[8]，详见图1。连续破冰过程中，船体可以持续前进，通过船首对冰表面的挤压使冰层破碎，详见图2[9]。反复突进式破冰通常发生在冰层较厚的情况下，船体需后退一段距离，后全速前进至船首置于冰层之上，靠船体自身重力将冰层压碎，如此反复。通常来讲，破冰船应具备在大部分航行时间里能够连续破冰航行的能力，因此，本文所研究的冰阻力仅指在连续破冰方式下船舶的冰阻力。

图1 连续破冰和反复突进式破冰

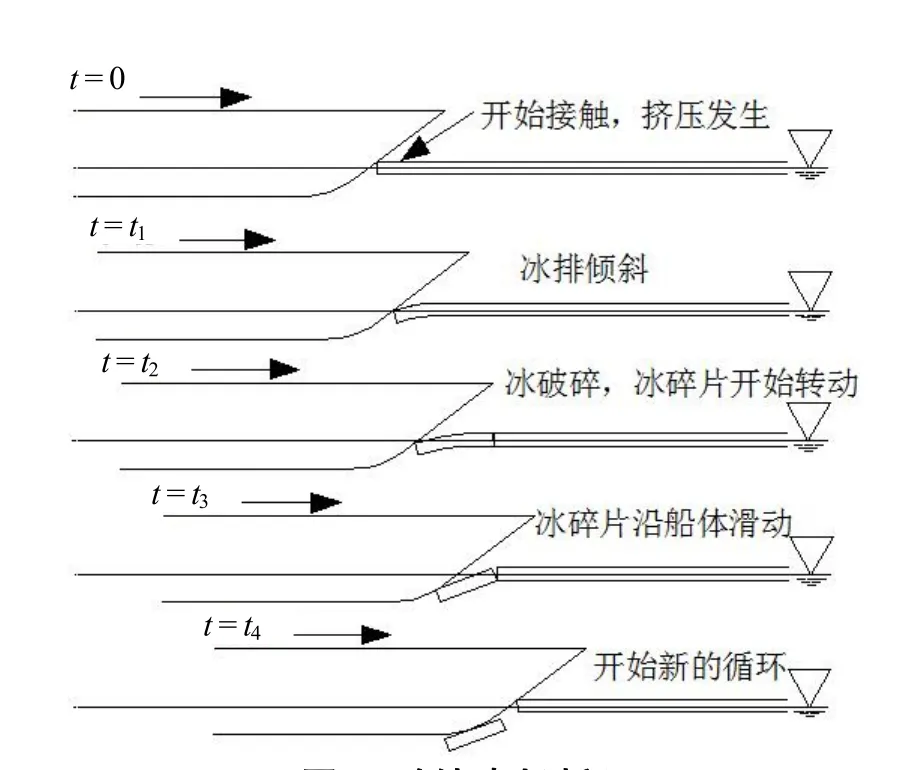
图2 连续破冰过程

图3显示了破冰船连续破冰过程中，船冰碰撞的受力情况。船首以一定速度与冰层接触，对冰层产生撞击并继续挤压冰层，致使冰层破碎。位于船体下部的碎冰，因本身具有浮力，会对船体产生一个升力。同时，碎冰沿船体向后排开会在船体与碎冰之间产生与速度相关的摩擦力[10]。1979年，Enkvist[11]首次指出海冰的这种复杂破碎形式，并建议将冰阻力相应的划分为破冰阻力、浸没阻力和摩擦阻力3个部分，以在阻力计算中最大程度的还原物理破冰过程并简化冰阻力的计算。

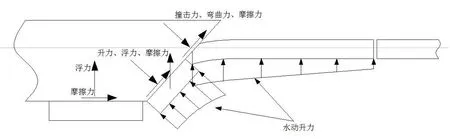
图3 船冰碰撞过程中受力分析

2.2 Lindqvist公式

1989年，Lindqvist[6]结合Enkvist的工作，在总结实船测量和模型试验结果的基础上，提出了Lindqvist公式。式中，把破冰阻力具体分为破冰力（包含破碎阻力RC、弯曲阻力RB）和依赖于速度的浸深阻力RS（也称为压沉阻力，可细分为摩擦阻力和势能损失），对不同成分的冰阻力分别进行经验评估。

Lindqvist公式计算的冰阻力中包含了冰层与船体挤压、破碎过程中产生的弯曲阻力，因此，其在阻力估算的过程中，不仅考虑了船体本身几何参数对冰阻力的影响，也考虑了冰的物理及力学属性的影响，如冰的弯曲强度及弹性模量等，更加符合实际情况，因此，Lindqvist公式对冰阻力估算的准确性有了一定的提高，也很好地反映出了船首形状对于冰阻力的影响。但是在实船测试中，很难将不同成分的阻力分开测得，因此很难分开验证各阻力成分估算的准确性[12]。

2.3 Riska公式

1997年，Riska提出了Riska公式[7]。Riska把冰的总阻力分为2个部分：敞水阻力和冰阻力。其中冰阻力进一步分为与速度相关的惯性阻力，一部分与速度无关的直接阻力。对于敞水阻力的估算方法已经成熟，这里不作讨论。对于其中的冰阻力，在总结波罗的海实船试验结果之后，给出一系列公式计算的经验系数，如表1所示。船体几何尺度的定义详见图4[13]。

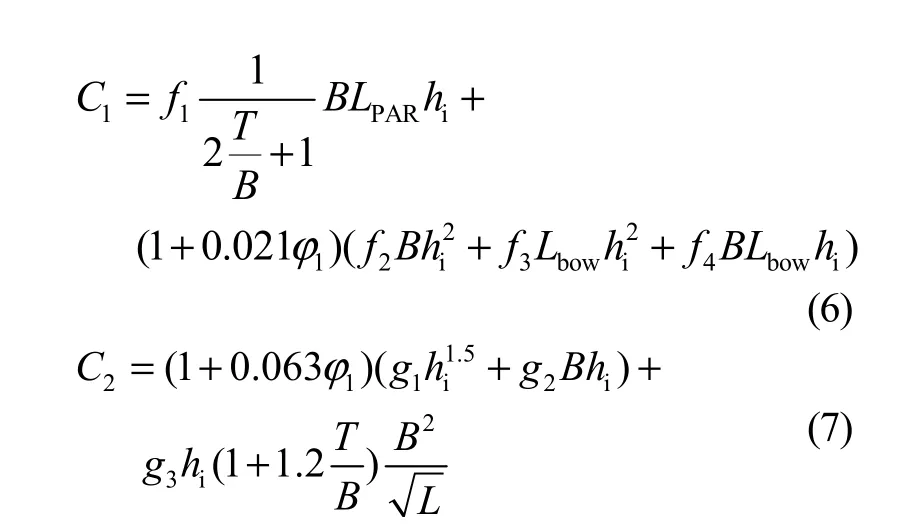
式中：f1～f4，g1～g3为经验系数。

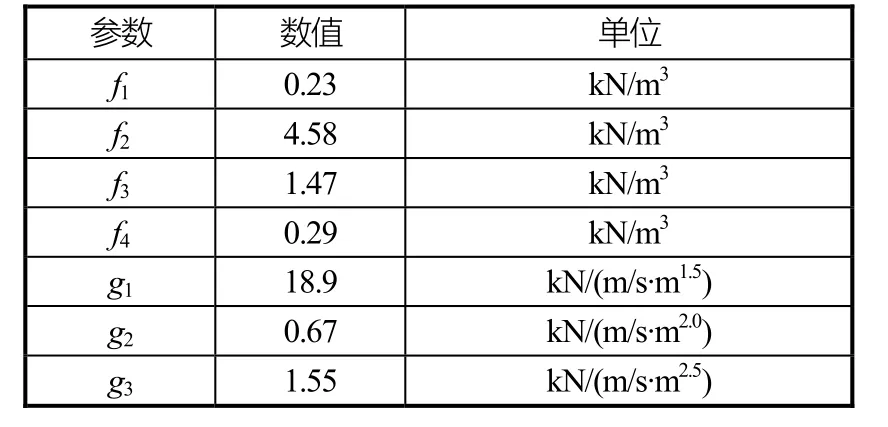
表1 Riska公式经验系数

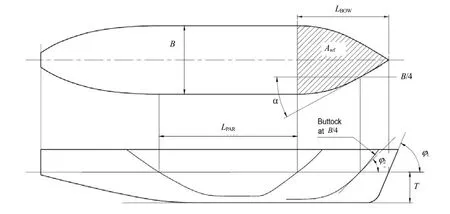
图4 船体几何尺度定义示意图

Riska公式把冰阻力分为敞水和冰阻力2个独立的部分，并且忽略两者之间的耦合关系[14]，但实际上两者之间是有相互影响的。且该公式计算的冰阻力不依赖冰的物理属性，仅考虑船舶本身尺度的影响。通过实际应用证明，该公式对于波罗的海航行的破冰船能够得到较为准确的结果。

2.4 冰参数经验公式计算法

冰材料是一种复杂材料，且在实际海况中，冰层厚度不均，强度不一，致使冰材料的力学及物理属性很难获得，在实船测试中，通常需要消耗大量的人力及时间，也因为这种复杂的属性，大大增加了模型试验中冰材料的制作难度及数值仿真中冰材料模拟的难度，对于某些考虑冰属性影响的经验公式的使用也带来了不便。但是，经过对各海域冰材料的统计分析，总结归纳出了冰参数的经验公式估算法，可以配合上述冰阻力估算使用，具体计算公式见式(8)～式(11)。

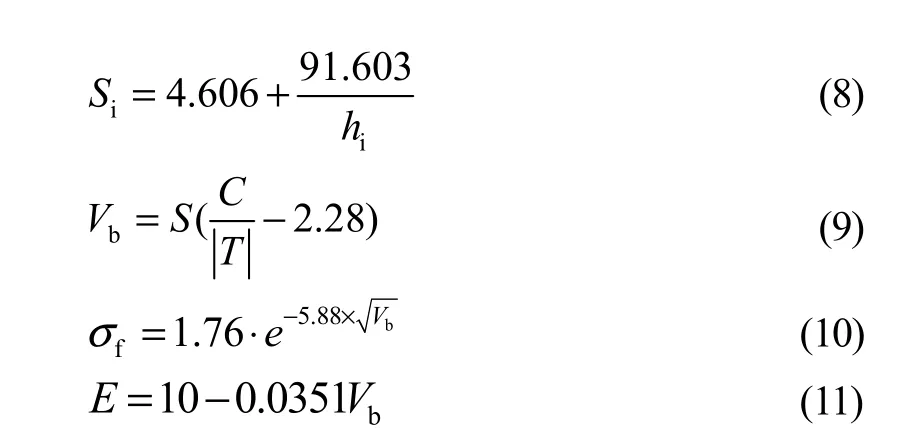
式中：Si表示每1 000 g海冰中的平均盐度。通常，当年冰盐度较高，多年冰因为盐度已析出，盐度较低；Vb为盐水体积；C为经验常数，根据温度的不同，选取不同的数值。通过冰材料各参数的经验公式计算法，可进一步得出各相关参数之间的关系，在本文后续计算中，本小节所论述的冰参数经验公式计算法将配合Lindqvist公式使用。

3 冰阻力模型试验

3.1 某型极地破冰船

本文以江南造船承建的某型极地破冰船为研究对象，其主要参数如表2所示。

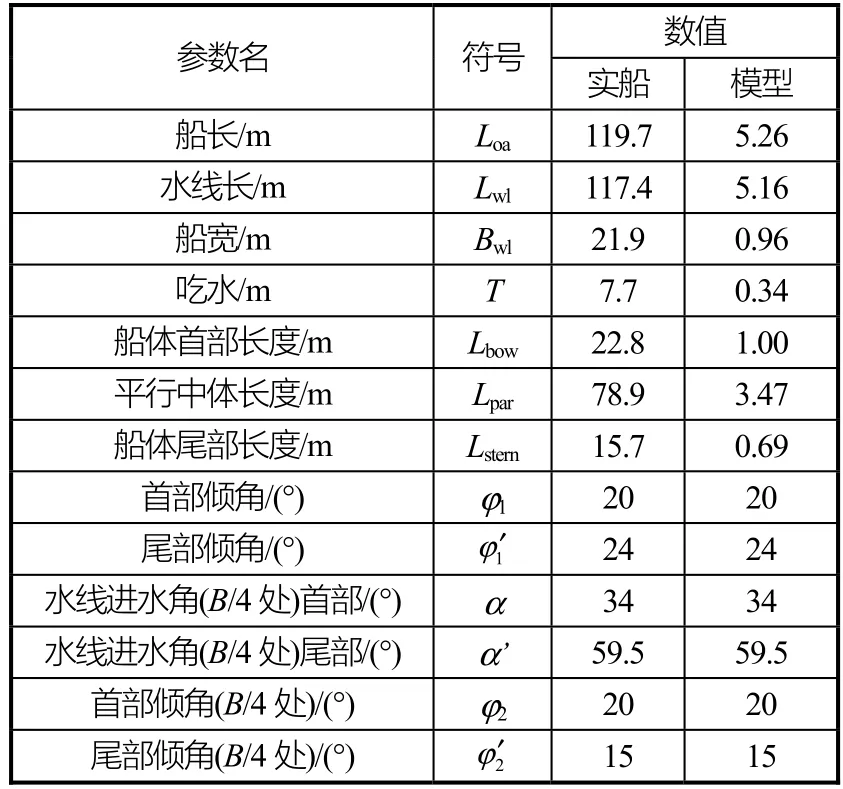
表2 该极地破冰船实船及模型的主要参数（缩尺比λ=22.764）

3.2 冰材料的模拟

试验目的为测试船舶在1.5 m冰厚且覆盖20 cm雪及0.9 m冰厚、覆盖20 cm雪情况下的船舶性能，通常情况下，为简化试验，用目标冰厚加上三分之一覆盖雪厚度的冰厚进行等效处理。因此，本次试验主要考察该破冰船在1.57 m及0.97 m冰厚情况下的破冰性能，试验中冰材料的模拟情况如表3所示，且为保证模型冰与实际冰能够有较高的相似性，模型冰的弹性模量与弯曲强度应保持一定的关系，Timco[19]在1980年曾提出类似的柯西相似准则，具体的弯曲强度及弹性模量数值以试验中实测为准。

表3 冰材料的模拟（缩尺比λ=22.764）

3.3 模型试验

本次模型试验主要测试该极地破冰船在平整冰情况下的连续破冰情况。为保证船模在冰池能够保持直线航行，限制船模的横荡及艏摇运动。首先将螺旋桨设置为目标转速，待运动稳定后可以获得相应工况下的冰总阻力，假定敞水阻力与冰阻力为独立2部分，总阻力减去敞水阻力部分即可得到模型冰阻力，再经过缩尺比换算即可获得实船冰阻力值。试验共设置3个螺旋桨转速，分别进行船首向前及船尾向前直线运动，记录试验结果。

4 结果与分析

4.1 Lindqvist公式和Riska公式计算结果与模型试验结果的比较

Lindqvist公式计算冰阻力时，冰属性参数多，且部分参数难以确定。经查阅相关冰阻力计算文献及船冰碰撞文献可知，在进行冰材料相关计算时，冰密度大致取值范围在850 kg/m3～950 kg/m3之间，本文取ρi=900 kg/m3，泊松比ν=0.3，摩擦系数取μ=0.1，弹性模量是经验值，不同尺度的船型差异较大，主要由模型试验测量获得。在模型试验中，通过对样本进行测量获得的弹性模量在 22 kPa～33 kPa范围内，按缩尺比换算到实际值为0.4 GPa～0.7 GPa，然而，海冰弯曲强度大致在0.1 MPa～1.5 MPa，且参考以前的船冰碰撞研究，破冰数值计算中普遍采用的弹性模量值E为8 GPa～9 GPa[20-21]，两者差别较大。分析造成这种差别的原因可能是弹性模量测量方式的不同。弹性模量的测量方法可分为静态测量法和动态测量法。静态测量结果分布范围为0.3 GPa～10 GPa，动态测量法得到的弹性模量的分布范围为6 GPa～10GPa[22]。这里试验中测得的弹性模量换算到实尺度大约在0.4 GPa～0.7 GPa之间，初步判定在试验中测量弹性模量使用的是静态测量法。然而，静态法是在加载之后测变形程度，在有效的静态测量时间区间内，有足够的时间让冰表现出粘塑性和弹脆变形2个阶段，所以静态的测量试验是只测量总变形的方法，并不能表现出冰的持续蠕变和弹性变形。据此，本次计算中采用的弹性模量则按照2.4中相关经验公式进行变换获得，根据已测得的试验冰材料的弯曲强度，由式(10)和式(11)获得相应弹性模量估算值，详细计算结果，如表4所示。

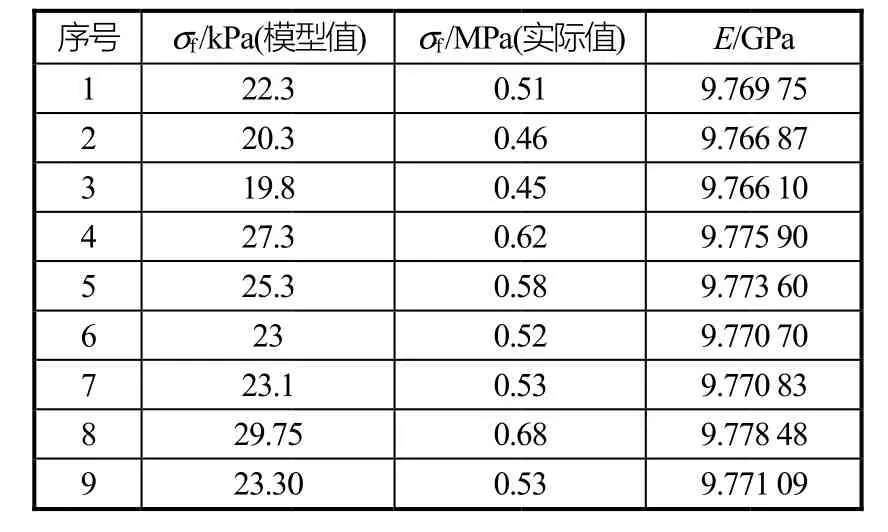
表4 弹性模量计算值

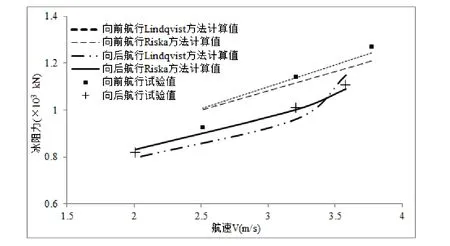
图5 冰厚为0.97 m时破冰阻力阻力结果比较

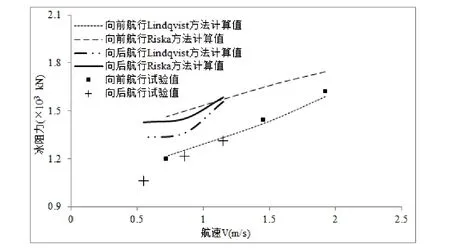
图6 冰厚为1.57 m时破冰阻力阻力结果比较

Lindqvist公式及Riska公式计算冰厚下极地破冰船的阻力计算结果如图5和图6所示。

由计算结果可以看出，在冰层密度、弯曲强度及弹性模量近似相等的情况下，速度越高，冰层越厚，阻力越大，这也是符合常规判断的。利用Lindqvist公式计算出的阻力也是满足这种变化规律的。船首向前与船尾向前航行的主要区别在于水线进水角和艏柱倾角的差别，图5和图6显示，在航速相近时，船尾向前航行时冰阻较船首向前时的冰阻力要小，可能是因为水线进水角大使得碎冰快速排开，减小了摩擦阻力部分。同时，可以明显看出Lindqvist公式在计算薄冰（hi=0.97 m）的情况下，准确度较高，在冰厚较大时（hi=1.57 m），尤其是船尾向前航行时准确性欠佳。Riska公式在高速薄冰的情况下有较高的准确性，在冰厚较大，速度较低时，冰阻力估算误差有增大的趋势。

4.2 敏感性分析

船体几何参数对冰阻力有重要的影响，研究各个参数对冰阻力的影响，可以为船舶设计初期的船体几何设计提供指导。本节主要考察了艏部倾角（船中纵剖面及B/4处）、水线进水角、艏部长度及平行中体长度对冰阻力的影响。以冰厚0.97 m，速度 3.21 m/s，艏部向前为例进行各参数敏感性分析，如图7所示。艏部倾角（船中纵剖面及B/4处）、艏部长度及平行中体长度与冰阻成正相关关系，而进水角的大小与冰阻力成反比关系。同为艏部倾角，在不同的估算方法中，其敏感性并不相同。在Lindqvist方法中，艏部倾角对结果的影响较大；在Riska方法中，各几何参量的变化对结果的影响均小于Lindqvist方法，且在Riska方法中，各参数对阻力的影响程度相似。从图7可以发现，进水角对冰阻有重要影响，进水角增大，冰阻力快速减小，但需要注意的是，进水角的增大也会增大船舶的敞水阻力，虽然敞水阻力在总阻力中所占的比重较小，但在设计时还应酌情考虑。