气井携砂数值分析方法
2018-07-30冯炜杨晨周福建张路锋苟梨田志达
冯炜 ,杨晨 ,周福建 ,张路锋 ,苟梨 ,田志达
(1.中国石油大学(北京)石油工程学院,北京 102249;2.中国石油大学(北京)油气资源与探测国家重点实验室,北京 102249;3.西南石油大学石油与天然气工程学院,四川 成都 610500;4.中国石油辽河油田分公司钻采工艺研究院,辽宁 盘锦 124010)
0 引言
气井生产过程中通常存在出砂的情况,但是现有的防砂措施达不到预期的效果,且防砂之后地层产能严重降低,因此对于疏松砂岩地层的气井而言,携砂生产是常用的解决方法。但是,当产气量小到无法携砂到地面时,砂粒就有可能堵塞产层或沉积井底;产气量过大时,砂粒的大量携出又会冲蚀井口设备[1]。因此,需制定合理的生产制度,既能有效携带出一定直径和密度的砂粒,又能确保采气设备不遭受冲蚀破坏。
截至目前,气井携砂模型都是基于砂粒的受力分析[2]或室内实验结果[3]建立的,以推导气井携砂临界速度[4]与临界产量公式为目的。邓绍强等[5]在受力分析基础上研究了不同流态下的受力表达式,计算得出临界参数;张书平等[6]分析了重力与浮力,得到了不同雷诺数范围的沉降末速度计算公式,并引入了形状修正系数;林琳等[7]建立了气井井筒携砂临界参数和出砂量预测的模型,较准确地计算了出砂量与冲砂周期;焦艳红等[8]自发研制垂直井筒携砂实验装置,模拟了现场砂粒携带实验并得到了最小携砂速度计算公式。以上成果都有助于加快气井携砂研究的进展,但目前对砂粒在井筒举升过程中的运动状态研究甚少,且研究与实际结合较少。
本次研究以砂粒受力分析[9]为基础,不仅建立了携砂临界参数模型,还建立了以单砂粒为研究对象的运动状态模型。结合气井的实际生产数据,应用模型进行了对比分析,得出井筒温度、压力、砂粒直径和密度等对气体携砂效果的影响规律以及砂粒的运动规律。
1 垂直气井携砂砂粒运动状态模型
本模型是基于砂粒的受力分析建立的。它不仅可以计算携砂的临界参数,也可求解砂粒在举升过程中任一深度的加速度和速度,即可得到砂粒的运动状态。
1.1 砂粒受力分析
力是改变物体运动状态的本质原因,分析砂粒的举升就要明确砂粒在垂直方向上的受力情况[10]。假设砂粒形状为理想圆球形颗粒,单个砂粒粒间互不干扰。当砂粒在井筒举升时,气体对颗粒的拖曳力FR、压差力Fp和浮力Ff为动力,颗粒自身重力Fg为阻力,其他的作用力,如附加质量力、Basset力、Saffman升力等,根据实际情况可忽略不计。
砂粒自身重力为
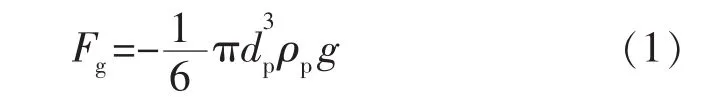
浮力为

压差力为

拖曳力为
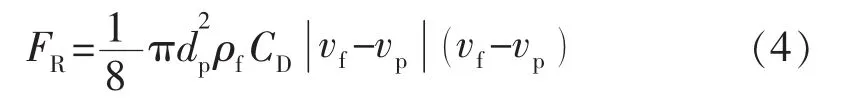
式中:dp为砂粒直径,m;ρp为砂粒密度,kg/m3;ρf为气体密度,kg/m3;为压力梯度,Pa/m;CD为阻力系数;vf为气体流速,m/s;vp为砂粒速度,m/s。
1.2 模型求解方法
在已知气井生产制度的前提下,求颗粒在任一深度的受力、加速度和速度,通过计算颗粒的速度,证明它是否能被携带出井口。具体方法是:将井筒划分n段,先根据条件求出每段的(即整个井的)速度分布;当速度小于0时,用编程语句输出“掉回井底”,即砂粒无法被携带到地面。如果砂粒在整口井的速度分布已求出,先通过判断所求深度在整个井筒的位置,再通过段内近似匀加速求出该深度时砂粒的速度。
1.3 具体计算步骤
1.3.1 温度分布
考虑地层与井筒的充分热交换,可以认为温度分布是线性变化的。
1.3.2 压力分布
具体计算步骤[11-12]:
1)设井深为h,井筒的分段数为

2)已知井口压力p0,井底压力pb,则压力迭代插值Δp为

3)进行第 i(i=1,2,3,…,n)段的压力计算。令第 i段的井筒压力为pi,则第i段的端点压力pmi为

4)求 p′mi
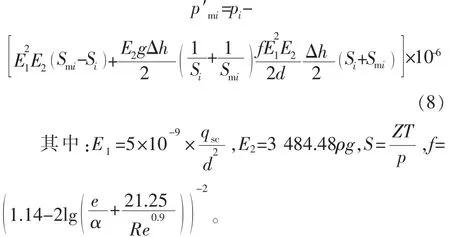
式中:p′mi为验证 pmi的变量,MPa;qsc为地面气体产量,m3/d;d为油管直径,m;为相对粗糙度(e为绝对粗糙度(0.001524m),α为管子内径);Re为雷诺数;f为管内摩擦因数;Z为气体压缩因子;g为重力加速度,m/s2。
当 pmi-p′mi<10-5时,则认为 pmi=p′mi;反之,令 pmi=p′mi,继续代入式(8)计算,直至满足 pmi-p′mi<10-5。
5)进行第1段压力计算时,令p1=p0,则第1段的端点压力pm1为p0+Δp;进行第2段及第i段的压力计算时,将上一段的端点压力赋予下一段的井筒压力,重复上面的计算,直到井底为止。
1.3.3 加速度
用FR+Ff+Fp-Fg=ma求加速度。用气井产量求出井底的气体初始速度计算井底拖曳力。
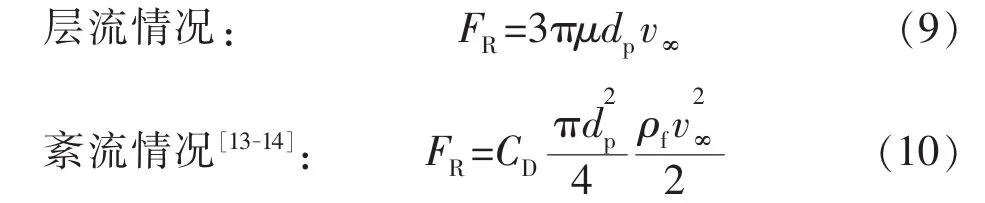
式中:m为砂粒的质量,kg;a为加速度,m/s2;v∞为气体与砂粒相对速度,m/s;CD为常数,一般取0.44。
1.3.4 速度分布
将整个井分为n段,从井底开始计算,假设砂粒在井底静止,每段运用,求出每段的起止速度。当n足够大时,即可近似地求出砂粒在整个井的速度分布。通过判断所求深度处于整个井筒的位置,即可计算出此深度的砂粒速度。
2 模型应用
2.1 临界流量计算模块
应用临界流量计算模块对某区块A井进行计算,结果见表1。临界流量是按1.3所述步骤进行计算的。通过改变井口压力、井口温度、砂粒直径、砂粒密度(砂子、加重剂、铁屑密度分别为2 500,4 300,7 900 kg/m3)、当前气井产量和油管直径等6个因素,对比临界流量的变化。已知A井井深4800m,井底温度140℃。
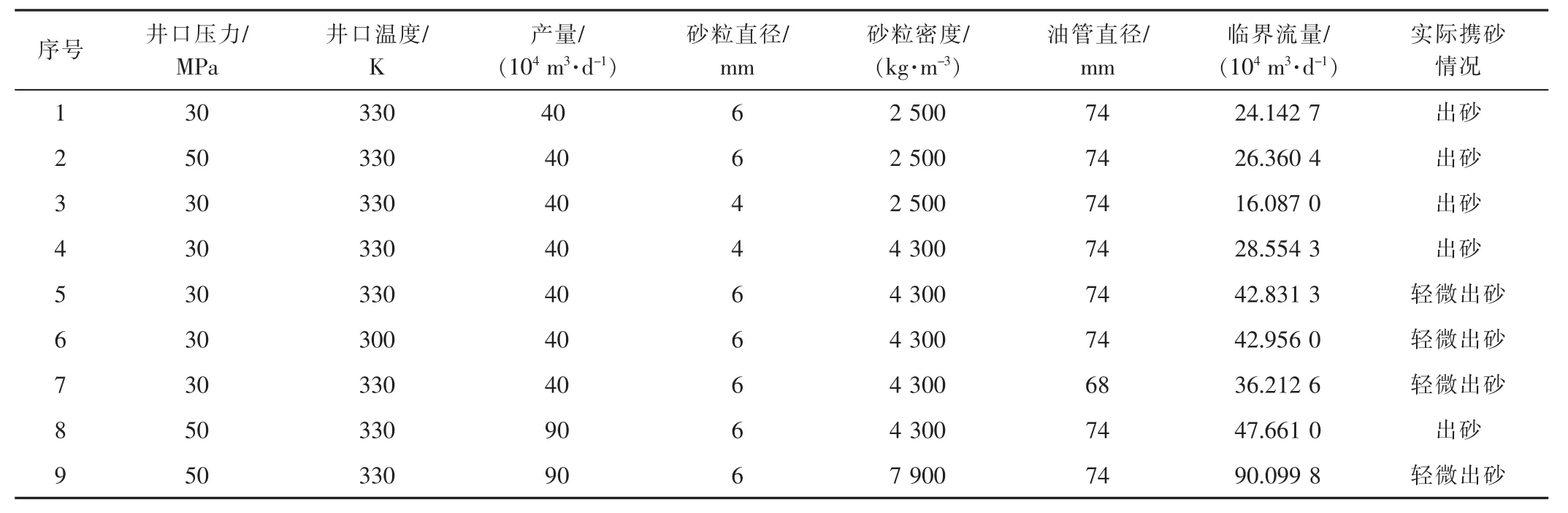
表1 临界流量计算模块计算结果
由表1的数据可以看出:井口温度、井口压力的变化对携砂临界流量的影响较小,且井口温度降低、井口压力升高会增大临界产量;砂粒直径的变化对临界产量变化的影响很大,砂粒直径增大30%,临界产量同样增加了近30%;砂粒密度对临界产量的影响也很大,且两者呈正比关系;油管直径也是影响临界产量的重要因素之一,小直径油管携砂更容易。
2.2 运动状态计算模块
运用砂粒运动状态计算模块,选取与表1中一致的参数进行砂粒加速度、速度的计算,对比得出砂粒的运动规律。
本文n=480 000,即将4 800 m的井分为480 000段,每段0.01 m。先假设砂粒在井底静止,初速度为0,计算结果见图1。由图可以看出:在井底静止的砂粒会存在一个瞬间加速过程,井底0.3 m内加速度可达到45~1 m/s2;接着,加速度变小,稳定在 10-3,10-4量级,速度的变化也趋于平缓,速度平缓加速上升。
为了明确瞬间变化的过程,选取井底部分数据绘制井底附近砂粒运动状态分布图(见图2)。
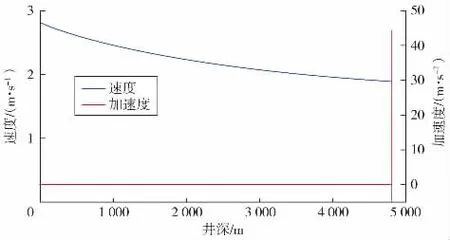
图1 初速度为0时砂粒运动状态分布
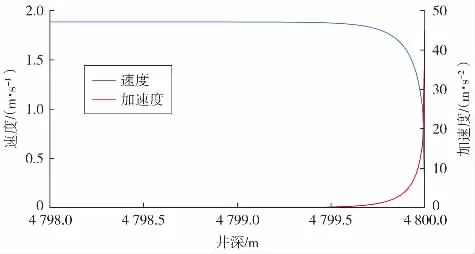
图2 初速度为0时井底附近砂粒运动状态分布
由图2可以清楚地确定整个变化过程。在井底0.50 m之内,因为气体流速较快,砂粒受到的拖曳力较大,砂粒的运动状态比较复杂。
保持其他数据不变,仅改变砂粒的初速度(砂粒的初速度为2 m/s),再进行程序运算。结果见图3。
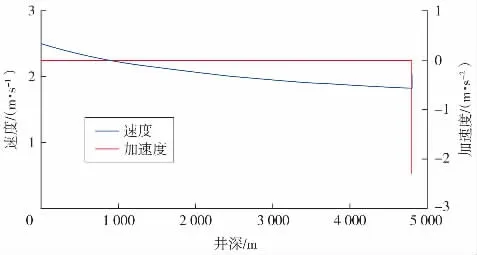
图3 初速度为2 m/s时砂粒运动状态分布
通过计算整口井的加速度、速度分布趋势,发现砂粒在井底先减速或稳定增速(加速度10-4数量级),增速过程与图1趋势基本一致。加速度转变点距离井底大概0.3 m左右,且因为砂粒存在初速度,井底附近砂粒的运动状态分布有所不同(见图4)。
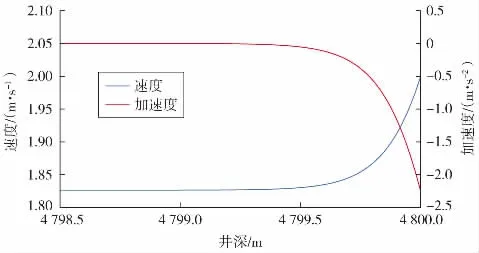
图4 初速度为2 m/s时井底附近砂粒运动状态分布
3 结论
1)该模型考虑因素全面,公式准确,迭代等计算过程全部由自编程序完成,计算的临界参数与实际相符,可指导现场生产。
2)通过单一变量法对比得出各因素对临界产量的影响程度及规律。临界产量与砂粒直径、密度、油管直径呈正比关系,且与砂粒的自身性质最相关。
3)从运动学出发,求解得到单个砂粒在井筒中被携带过程的运动状态图版,明确任一深度处砂粒的运动情况,使对气井携砂过程的认识进一步提升。
4)本文就气井携砂问题提出了新的计算思路,此方法也可用于探究砂粒运动对套管的磨损问题。
