戈壁集料级配优化试验及充填材料制备*

王志凯，王贻明，吴爱祥，马浩吉，刘 权，杨锡祥

(1.北京科技大学 金属矿山高效开采与安全教育部重点实验室，北京 100083;2.长沙矿山研究院有限责任公司，湖南 长沙 410012；3.伽师县铜辉矿业有限责任公司，新疆 喀什市 844000)

0 引 言

目前随着浅部资源的逐渐枯竭，越来越多的矿山开始研究深部开采，低成本固废材料应用于深部矿山充填领域已经成为国内研究的重点[1-2]。以矿山充填材料的历史发展、所用物料等方面看，可归为固废的综合利用[3-5]。

经过大量研究表明，利用戈壁集料制备矿山充填材料是可行的。关于戈壁集料的应用，李军峰[6]探讨了杜达铅锌矿高硫尾砂与戈壁集料制备矿山充填材料，并对充填料破碎、筛分等工艺环节进行了优化改造；李公成等[7]研究了以戈壁集料为粗骨料制备的充填体凝结性及流动性，并对配比范围做出预测；曹心[8]等研究了戈壁集料与水泥、粉煤灰制备的充填料浆自流输送的性能，并得到满足自流输送要求的充填配比；李安平[9]探讨了全尾砂-戈壁集料配比优化研究，为当地充填系统的改造提供了理论依据。以上研究所提出的观点为研究戈壁集料与全尾砂制备充填材料进一步指明了方向。

虽然对戈壁集料的研究已经取得了重大进步，但是目前关于戈壁集料级配优化及制备矿山充填材料实验研究少有报道。本文以新疆当地戈壁集料及某铜矿充填所用的高含泥全尾砂为主要原料，进行戈壁集料级配优化试验和充填材料制备试验，并利用二次多项式回归分析对全尾砂戈壁充填材料的塌落度和单轴抗压强度进行分析，试验结果为当地矿山充填奠定理论基础。

1 试 验

1.1 试验材料

(1) 全尾砂。选自该矿山选厂，对全尾砂进行物理参数分析如表1所示，粒度分析如图1所示。

从图1可知全尾砂中-20 μm的颗粒含量为29.8%，则全尾砂材料整体饱水率较好[10]。

(2) 戈壁集料。选自新疆地区的砾石，其经过长年风蚀、雨淋作用，棱角逐渐被磨圆。戈壁集料的松散堆积密度为1.75 t/m3，密实堆积密度为1.97 t/m3，孔隙率为34.9%，粒径分析结果见图2。

表1 物料物理参数

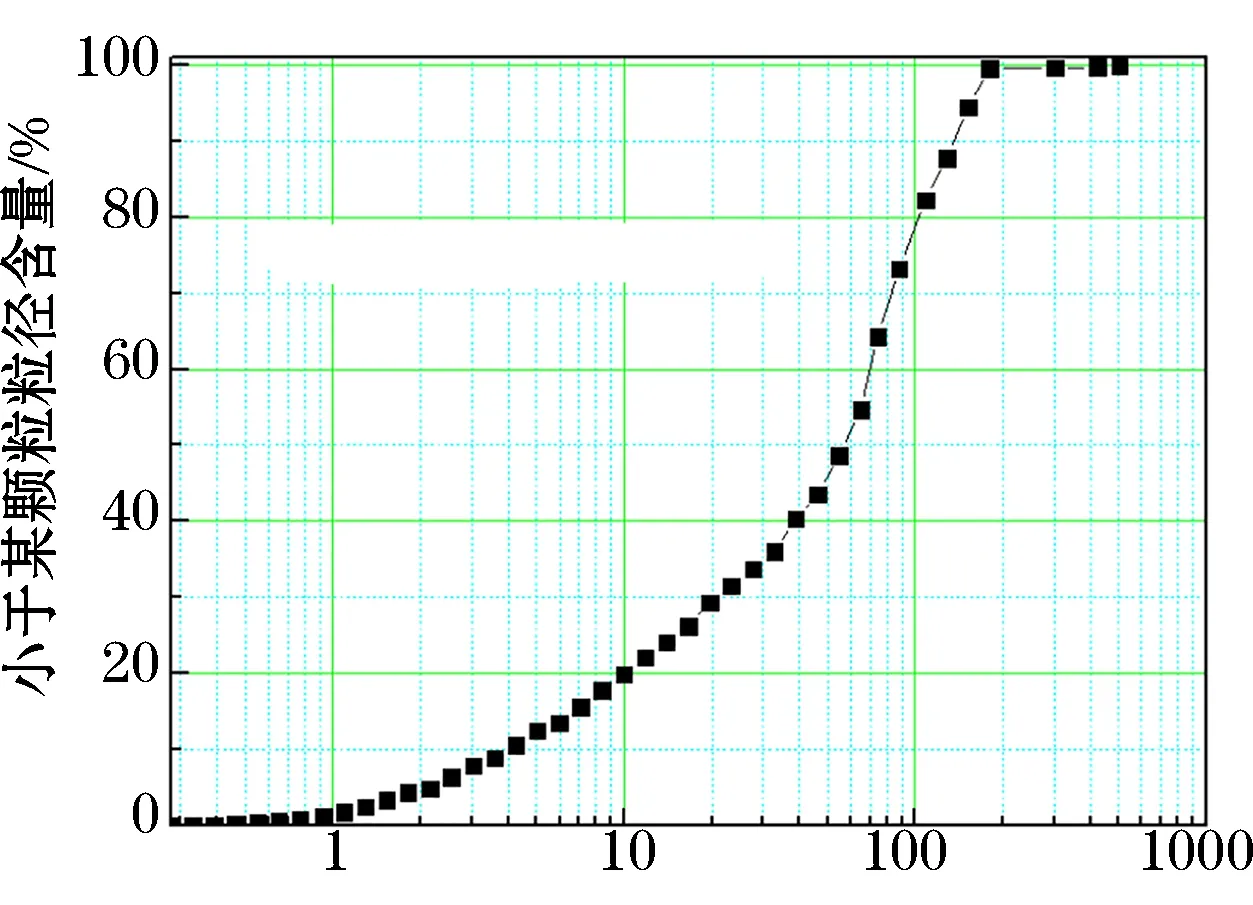
图1 全尾砂粒度分析结果

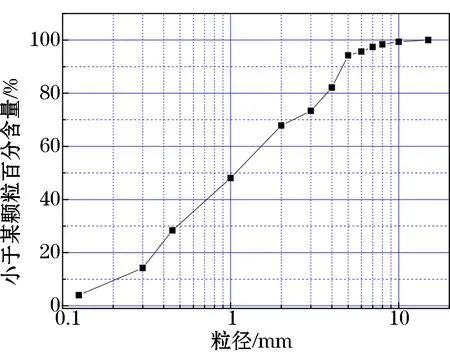
图2 戈壁集料粒度分析结果

1.2 试验方法

试验分为2个部分，分别为戈壁集料级配优化试验和充填材料配比试验。将原材料配置充填料浆，将配比好的料浆倒入砂浆搅拌锅内，按 GB/T50080-2002标准搅拌一定时间后注入70.7 mm×70.7 mm×70.7 mm标准三联试模中并振荡刮平。脱模后放入养护箱中进行标准养护(温度20℃±1℃、湿度≥90%)，按时测定试块相应龄期强度，每个龄期强度测3个试块，并取其平均值，并对充填料浆进行塌落度试验。所得试验结果运用二次多项式进行回归分析。

2 戈壁集料级配优化试验

试验以浓度76%、添加剂剂量2%、砂灰比6、骨料比3为固定条件，对初始砂、0～4 mm(标准建筑砂，含泥物质经洗除)、0～12 mm 及4～12 mm四种不同级配戈壁集料的充填材料进行对比，选出最优戈壁集料级配(见图3)。

由图3可知，A组(不添加)充填体强度与养护时间成正相关，但28 d强度不足1 MPa，不能满足当地生产要求；B组(0～4 mm)充填体强度与养护时间呈正相关，3 d强度达到5 MPa，28 d强度达到11.05 MPa，且后期强度增长较快，但此戈壁集料价格较贵；C组(0～12 mm)充填体3 d强度略低于D组(4～12 mm)充填体，但其后期强度增长速率大于D组，28 d强度达到6 MPa，高出D组充填体近2 MPa。因此，从降低原料成本、满足充填材料强度要求、集料利用率3方面综合考虑，选择C组(0～12 mm)戈壁集料制备充填材料更为合理。

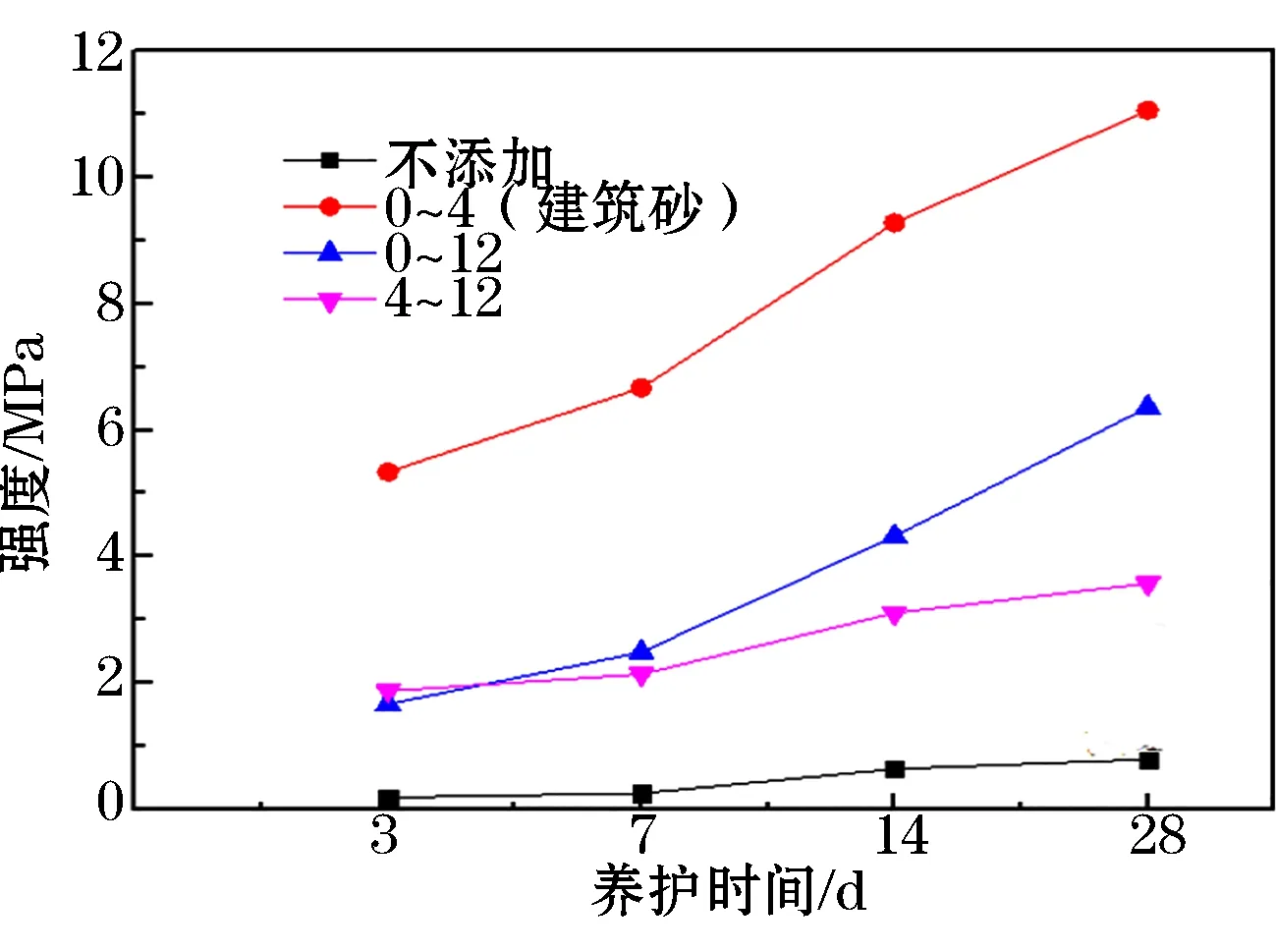
图3 不同级配戈壁集料强度曲线

3 充填材料配比试验

3.1 充填材料配比方案

当地采矿方法为下向VCR嗣后膏体充填采矿法，充填作业分为假顶部位充填和嗣后充填。其中(假顶)充填体28 d目标强度为4 MPa，(嗣后)充填体28 d目标强度为1 MPa。

(假顶)充填材料配比方案如表2所示，其中浓度变化范围为75%～80%，砂灰比范围为4～9，骨料比范围为3～8，添加剂范围为1%～2.5%。

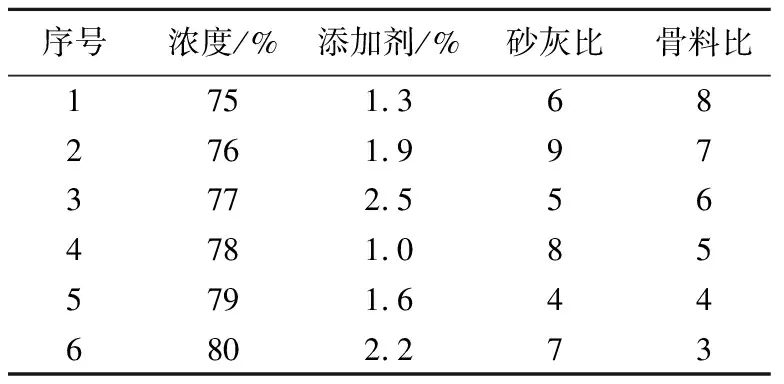
表2 (假顶)膏体配比试验

(嗣后)充填材料配比方案如表3所示，其中浓度变化范围为74%～79%，砂灰比范围为8～18，骨料比范围为2～7，添加剂范围为1%～2.5%。

3.2 (假顶)充填材料配比试验结果与分析

3.2.1 试验结果回归分析

(假顶)充填材料配比试验见表4，由表4可知，塌落度、强度与浓度、砂灰比、骨料比、添加剂剂量之间均为非线性关系。常用的非线性回归方法有幂函数回归、指数回归、对数回归以及多项式回归等，通过DPS(Data Processing System)数据处理软件对数据进行处理，发现二次多项式回归的相关性最高[7]，因此采用二次多项式逐步回归对数据进行分析。

通过DPS数据处理软件建立塌落度与浓度、砂灰比、骨料比和添加剂之间二次多项式回归公式，如式1所示。拟合方程的相关系数R=0.9998，显著水平p=0.031<0.05。

y1=-17.5924+45.353x2-11.0803x22

-0.0747x32+0.1053x42

(1)

式中，y1为塌落度(假顶)，cm；x2为添加剂剂量，%；x3为砂灰比；x4为骨料比。

通过数据拟合可以看出，(假顶)充填体的塌落度主要受砂灰比、骨料比和添加剂剂量这3个因素影响。在拟合过程中，浓度这个因素被剔除，表示浓度在75%～80%之间变化对充填体塌落度的影响较小。塌落度回归方程的残值分析如表5所示，残值与观测值的比均小于0.7%，表示回归方程误差极小，对试验拟合结果较好。

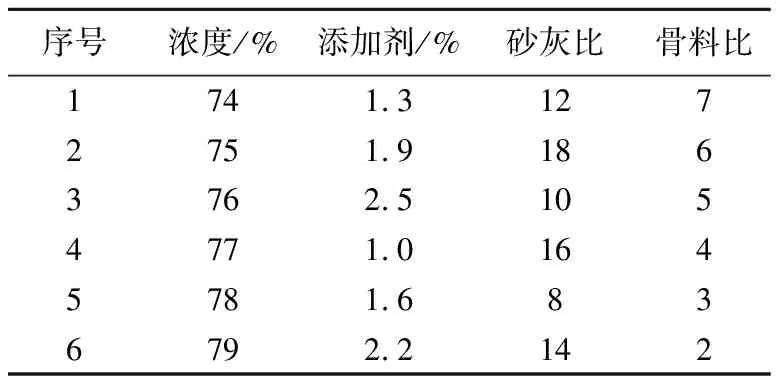
表3 (嗣后)膏体配比试验

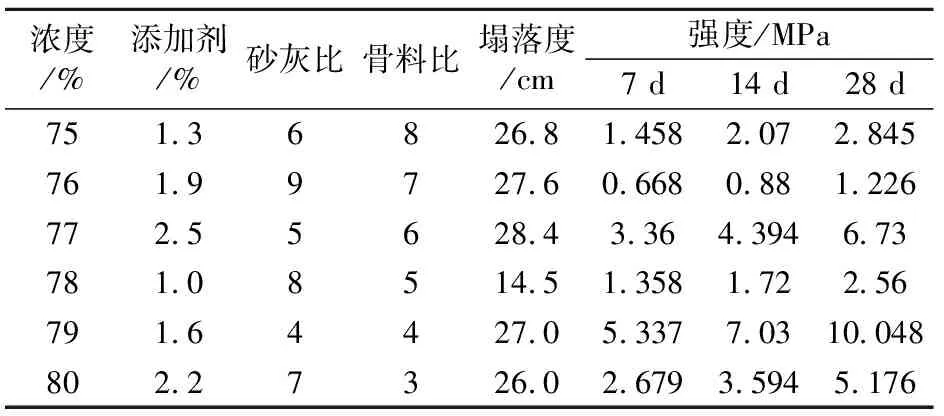
表4 (假顶)膏体配比试验结果

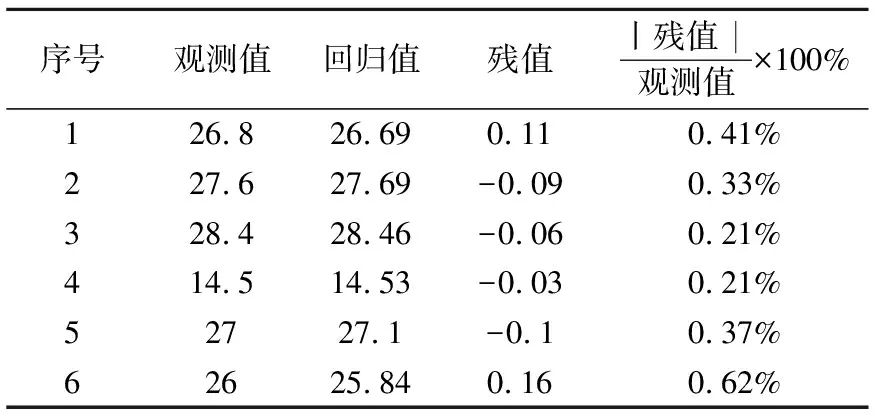
表5 (假顶)塌落度残值分析

注：残值=观测值-回归值，残值为检测各值的回归差异度。

通过DPS数据处理软件建立试块7 d强度与浓度、砂灰比、骨料比和添加剂之间二次多项式回归公式(见式(2))。拟合方程的相关系数R=1.0000，显著水平p=0.0036<0.05。

y2=-0.8792-2.7755x3+0.002335x12

+0.1579x32+0.001709x1x2

(2)

式中，y2为7 d强度(假顶)，MPa；x1为浓度，%；x2为添加剂剂量，%；x3为砂灰比。

通过数据拟合可以看出，(假顶)充填体的7 d强度主要受浓度、砂灰比和添加剂这3个因素影响。在拟合过程中，骨料比这个因素被剔除，说明骨料比在3～8范围内变化对充填体7 d强度的影响较小。7 d强度回归方程残值分析如表6所示，残值与观测值的比均小于0.5%，表示回归方程误差极小，对试验拟合结果较好。

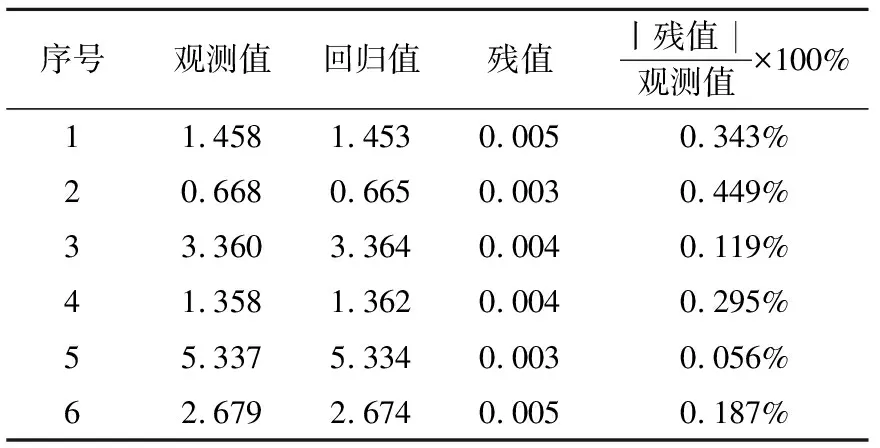
表6 (假顶)充填体7 d强度残值分析

通过DPS数据处理软件建立试块14 d强度与浓度、砂灰比、骨料比和添加剂之间二次多项式回归公式，如式(3)所示。拟合方程的相关系数R=0.9997，显著水平p=0.0374<0.05。

y3=-19.0272+0.4649x1-3.4851x3

+0.1903x32+0.02957x2x3

(3)

式中，y3为14 d强度(假顶)，MPa；x1为浓度，%；x2为添加剂剂量，%；x3为砂灰比。

通过数据拟合可以看出，(假顶)充填体的14 d强度主要受浓度、砂灰比和添加剂这3个因素影响。在拟合过程中，骨料比这个因素被剔除，说明骨料比在3～8范围内变化对充填体14 d强度的影响较小。14 d强度回归方程残值分析如表7所示，残值与观测值的比均小于3.3%，说明回归方程误差较小，对试验拟合结果较好。

通过DPS数据处理软件建立试块28 d强度与浓度、砂灰比、骨料比和添加剂之间二次多项式回归公式，如式(4)所示。拟合方程的相关系数R=0.9999，显著水平p=0.0215<0.05。

y4=24.9564-4.5364x3+0.2324x32

-0.06013x42+0.07058x2x3

(4)

式中，y4为28 d强度(假顶)，MPa；x2为添加剂剂量，%；x3为砂灰比；x4为骨料比。

通过数据拟合可以看出，(假顶)充填体的28 d强度主要受添加剂、砂灰比和骨料比这3个因素影响。在拟合过程中，浓度这个因素被剔除，说明浓度在75%～80%范围内变化对充填体28 d强度的影响较小。28 d强度回归方程残值分析如表8所示，发现残值与观测值的比均小于1.6%，说明回归方程误差较小，对试验拟合结果较好。

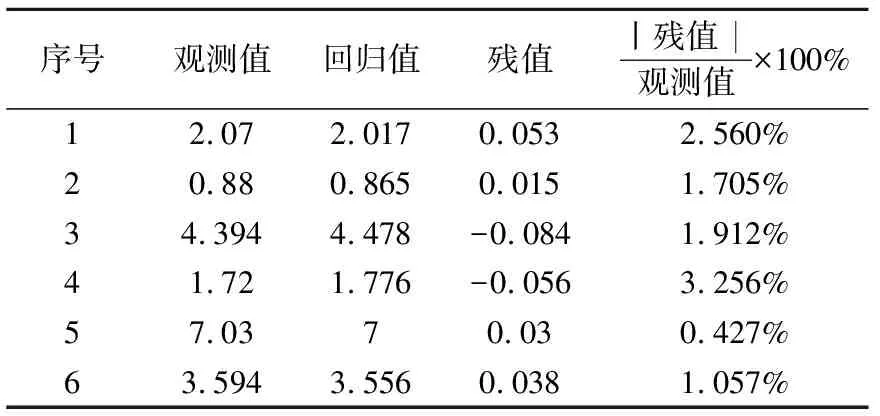
表7 (假顶)充填体14 d残值分析

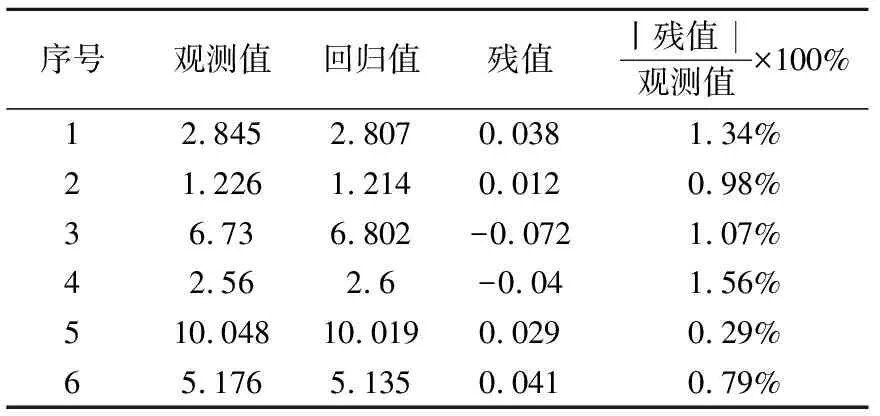
表8 (假顶)膏体28 d强度残值分析

3.2.2 优化配比

通过限定约束条件x1=75～80，x2=1～2.5，x3=4～9，x4=3～8，利用Excel软件对式(4)进行带约束条件的非线性规划，得到充填材料28 d的最优强度值及对应的配比，优化结果如表9所示。

表9 (假顶)膏体28 d强度最优值预测

从优化结果可以得出，当添加剂为2.5%、砂灰比为4、骨料比为3时，充填材料的28 d强度达到10.7 MPa。

3.3 (嗣后)充填材料配比试验结果与分析

3.3.1 试验结果回归分析

(嗣后)膏体最佳配比试验结果见表10。

通过DPS数据处理软件建立塌落度与浓度、砂灰比、骨料比和添加剂之间二次多项式回归公式，如式(5)所示。拟合方程的相关系数R=0.9999，显著水平p=0.0176<0.05。

y5=25.8253-0.01388x32+0.03143x42

+0.1407x2x3-0.08406x2x4

(5)

式中，y5为塌落度(嗣后)，cm；x2为添加剂剂量，%；x3为砂灰比；x4为骨料比。

通过数据拟合可以看出，(嗣后)充填材料的塌落度主要受砂灰比、骨料比和添加剂这3个因素影响。在拟合过程中，浓度这个因素被剔除，说明浓度在74%～79%之间变化对充填体塌落度的影响较小。塌落度回归方程的残值分析如表11所示，发现残值与观测值的比均小于0.08%，表示回归方程误差极小，对试验拟合结果较好。

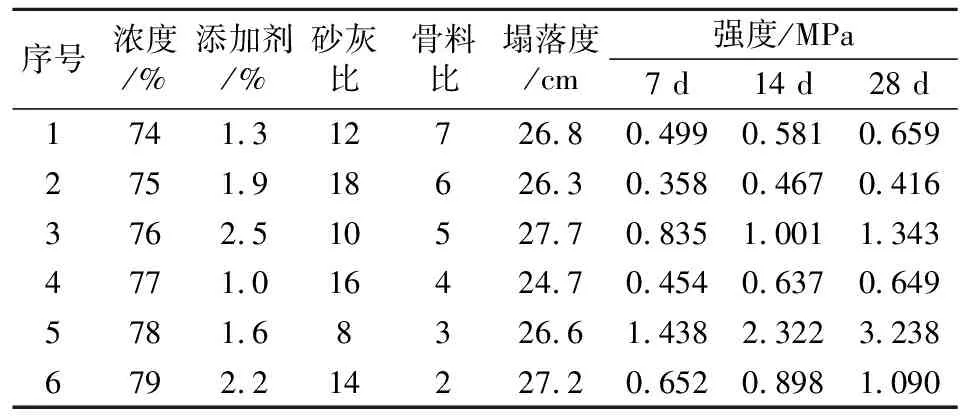
表10 (嗣后)膏体最佳配比试验结果

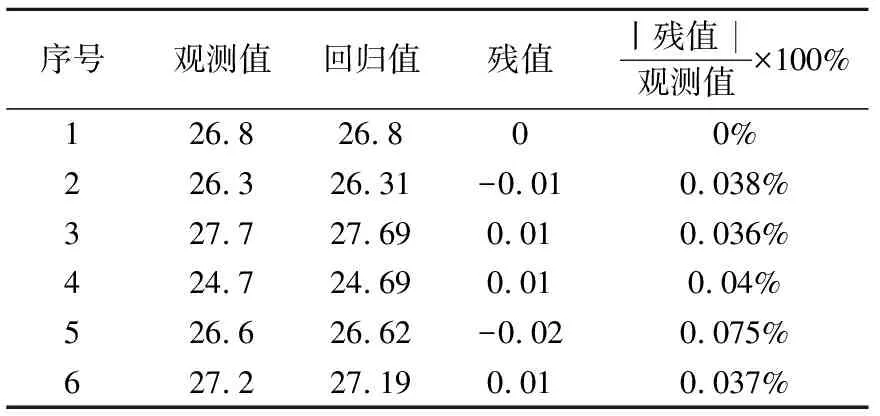
表11 (嗣后)塌落度残值分析

通过DPS数据处理软件建立试块7 d强度与浓度、砂灰比、骨料比和添加剂之间二次多项式回归公式，如式(6)所示。拟合方程的相关系数R=0.9995，显著水平p=0.0484<0.05。

y6=4.4074-0.4581x3+0.01433x32

-0.000765x1x4-0.009745x2x4

(6)

式中，y6为7 d强度(嗣后)，MPa；x1为浓度，%；x2为添加剂剂量，%；x3为砂灰比；x4为骨料比。

7 d强度回归方程残值分析如表12所示，发现残值与观测值的比均小于4%，说明回归方程误差小，对试验拟合结果较好。

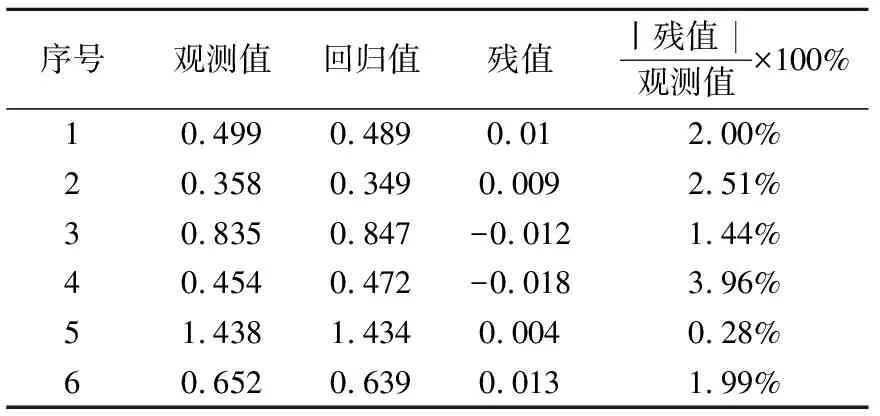
表12 (嗣后)膏体7 d强度残值分析

通过DPS数据处理软件建立试块14 d强度与浓度、砂灰比、骨料比和添加剂之间二次多项式回归公式，如式(7)所示。拟合方程的相关系数R=1.0000，显著水平p=0.0055<0.05。

y7=8.4426-0.9938x3+0.03203x32

+0.01531x2x3-0.08695x2x4

(7)

式中，y7为14 d强度(嗣后)，MPa；x2为添加剂剂量，%；x3为砂灰比；x4为骨料比。

通过数据拟合可以看出，嗣后充填材料的14 d强度主要受骨料比、砂灰比和添加剂这3个因素影响。在拟合过程中，浓度这个因素被剔除，说明浓度在74%～79%之间变化对充填体14 d强度的影响不大。回归方程残值分析如表13所示，发现残值与观测值的比均小于0.7%，说明回归方程误差较小，对试验拟合结果较好。

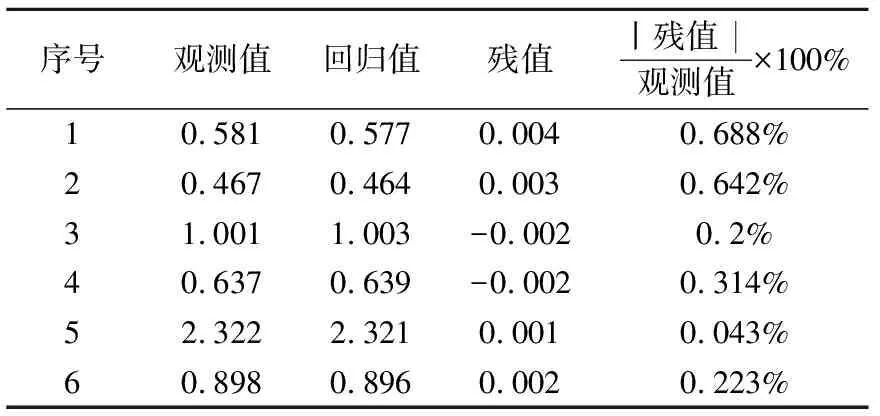
表13 (嗣后)膏体14 d强度残值分析

通过DPS数据处理软件建立28 d强度与浓度、砂灰比、骨料比和添加剂之间二次多项式回归公式，如式(8)所示。拟合方程的相关系数R=1.0000，显著水平p=0.0021<0.05。

y8=12.2021-1.4556x3+0.04626x32

+0.0239x2x3-0.1221x2x4

(8)

式中，y8为28 d强度(嗣后)，MPa；x2为添加剂剂量，%；x3为砂灰比；x4为骨料比。

通过数据拟合可以看出，(嗣后)充填体28 d强度主要受添加剂、砂灰比和骨料比这3个因素影响。在拟合过程中，浓度这个因素被剔除，说明浓度在74%～79%之间变化对充填体28 d强度的影响较小。28 d强度回归方程残值分析如表14所示，发现残值与观测值的比均小于0.25%，表示回归方程误差较小，对试验拟合结果较好。

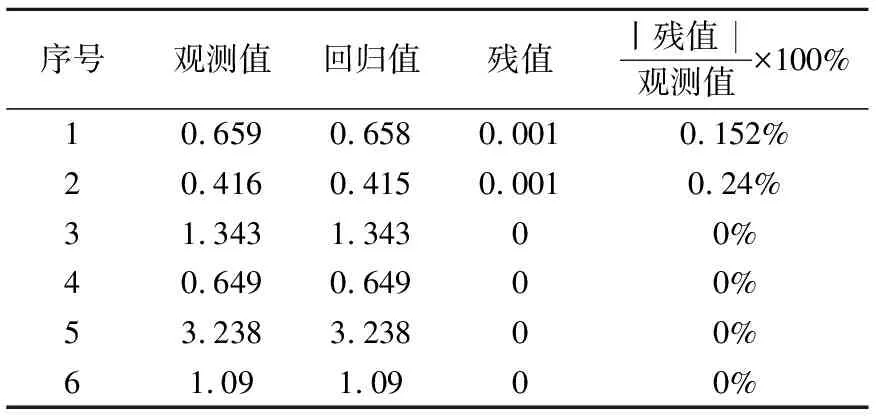
表14 (嗣后)膏体28 d强度残值分析

3.3.2 优化配比

通过限定约束条件x1=74～79，x2=1～2.5，x3=8～18，x4=2～7，利用Excel数学软件对式8进行带约束条件的非线性规划，得到试块28 d强度最优值及对应的配比，优化结果如表15所示。

可以看出，当添加剂剂量为1%、砂灰比为8、骨料比为2时，(嗣后)充填体的28 d强度达到3.5 MPa。

表15 (嗣后)膏体28 d强度最优值预测

4 结 论

(1) 通过戈壁集料级配优化试验，选出戈壁集料粒级为0～12 mm制备矿山充填材料更为合理。

(2) 通过二次多项式回归分析，发现影响(假顶)充填体塌落度和各龄期强度因素中，74%～79%的浓度对塌落度和28 d抗压强度影响较小，骨料比变化对7，14 d抗压强度影响较小。影响(嗣后)充填体塌落度和各龄期强度因素中，74%～79%的浓度对充填体塌落度及14，28 d抗压强度影响较小，各因素变化对7 d强度影响都较明显。

(3) 通过Excel数学软件得到：当浓度为74%～79%，添加剂为2.5%、砂灰比为4、骨料比为3时，(假顶)充填体28 d强度达到10.7 MPa；当浓度为74%～79%，添加剂为1%、砂灰比为8、骨料比为2时，(嗣后)充填体的28 d强度达到3.5 MPa。