列车运行下综合交通枢纽站房结构振动分析
2018-07-28李正川冉汶民李小珍
李正川,冉汶民,易 兵,李小珍,张 迅
(1.中铁二院重庆勘察设计研究院有限责任公司,重庆 400023;2.西南交通大学土木工程学院,成都 610031;3.重庆城市综合交通枢纽开发投资有限公司,重庆 430000)
随着交通运输的快速发展,综合交通枢纽的环境振动问题已引起人们的广泛关注。本文将对综合交通枢纽站房的振动问题展开分析。国内外学者对站房结构在列车荷载激励下的振动响应进行了广泛的研究,且多采用施加时程荷载得到振动响应的分析方法。翟婉明[1-3]、李小珍[4-5]、张迅[6]等学者对车辆-轨道-桥梁动力学耦合效应进行了深入研究,在这些研究成果基础上,可以对站房结构的振动加速度响应进行求解。陈行[7]、程海根[8]和程烨[9]等通过施加时程激励和建立预测模型的方法对列车产生的振动进行了数值模拟。高日[10-12]等通过建立车桥耦合模型计算得到时程荷载,并施加于框架模型,初步探索了“站桥合一”站房结构振动响应的分析方法。
本文采用频域分析方法对综合交通枢纽的振动响应进行分析, Janssens[13]、Harrison[14]和吴天行[15]等建立了车辆-轨道-桥梁耦合分析模型,并得到了扣件力的频域解。笔者[16]曾采用频域分析模型分析了轨道梁的振动响应,但并未进一步分析站房结构的振动响应问题。由于车站的土体模型非常庞大,故采用分离模型,分别建立车辆-轨道数值分析模型、轨道-土体有限元模型、站房结构有限元模型。通过车辆-轨道模型计算得到频域内的轮轨力解,再施加到轨道-土体模型求解得到站台的振动响应,最后将土体响应结果作为激励荷载施加到站房柱底,计算得到站房的振动响应。本文为综合交通枢纽站房结构的振动响应分析提供了一种分析方法,其计算结果可以为综合交通枢纽的减振设计提供参考。
1 车辆-轨道耦合模型
本文主要考虑1~80 Hz垂向振动,故车辆-轨道模型也只考虑垂向作用。图1为车辆-轨道垂向耦合模型,其包含了1/8集总参数车辆模型、轨道模型两部分。在轨道不平顺R的激励下,可以得到轮轨力为
(1)
式中,αw、αt、αc分别为车轮、钢轨和轮轨接触弹簧的位移导纳,即单位荷载作用在其位置上的位移响应。
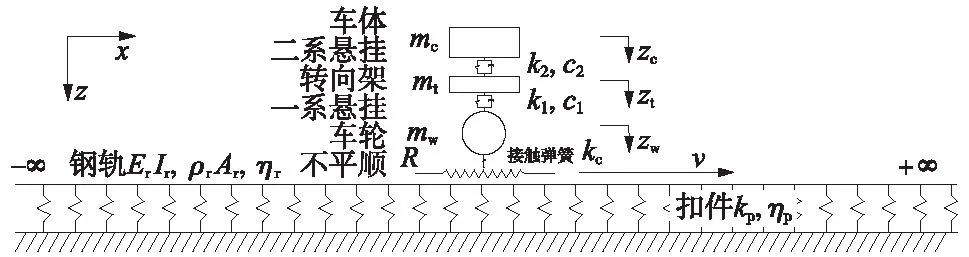
图1 车辆-轨道耦合模型
1.1 车辆模型
车辆模型包含了一系、二系悬挂系统。1/8集总参数车辆模型包含了1/8车体、1/4转向架和单个车轮。建立如图1所示的坐标系,建立运动微分方程

(2)

假定Z=Z(ω)eiωt,F=F(ω)eiωt,针对1/8车体、1/4转向架和单个车轮分别建立运动微分方程式得到式(3)~式(5)
-ω2mczc(ω)+c2ωi(zc(ω)-zt(ω))+
k2(zc(ω)-zt(ω))=0
(3)
-ω2mtzt(ω)+c1ωi(zt(ω)-zw(ω))+k1(zt(ω)-
zw(ω))-c2ωi(zc(ω)-zt(ω))-k2(zc(ω)-
zt(ω))=0
(4)
-ω2mwzw(ω)-c1ωi(zt(ω)-zw(ω))-k1(zt(ω)-
zw(ω))=F(ω)
(5)
式中,下标c、t和w分别代表车体、转向架和车轮;c1、k1分别为一系悬挂阻尼和刚度;c2、k2分别为二系悬挂阻尼和刚度。
联立式(3)~式(5)可以求解出位移导纳
αw=Zw/F
(6)
1.2 轨道模型和轮轨接触模型
将钢轨视为无限长Euler-Bernoulli梁,Er、ρr、Ir、Ar和ηr分别表示其弹性模量、密度、截面惯性矩、截面积和损耗因子。不考虑轨道板和底座板,将扣件视为带结构阻尼的线性弹簧,其间距为d,损耗因子ηp,刚度kp,扣件底端直接固定。参考文献[12]的计算方法,可以得到钢轨导纳αt
(7)

本文采用Remington[17]模型分析车轮和钢轨之间的垂向作用,可得轮轨接触导纳
(8)
式中,E为车轮弹性模量;ν为钢轨泊松比;Rw和RR分别为车轮和钢轨半径;ξ和θ为与车轮和钢轨半径有关的系数。
2 有限元模型建立
2.1 轨道-土体有限元模型
该模型以重庆沙坪坝综合交通枢纽为工程背景。轨道-土体计算模型尺寸为210 m×100 m,见图2。土体厚度20 m,共2层土体,第1层为泥岩,厚7.6 m,第2层为砂岩,厚12.4 m。该模型共7条轨道,其中轨道4和轨道5为正线(列车不停站,直接通过的线路),其余轨道为到发线。轨道结构为减振型双块式无砟轨道,钢轨采用SHELL63单元模拟,道床板和底座板采用SOLID45单元模拟,扣件、减震垫和滑动层采用COMBIN14单元模拟。土体采用SOLID45单元模拟,具体的材料参数见表1。
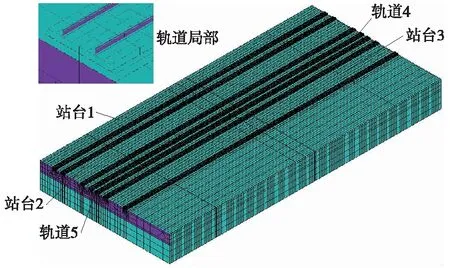
图2 轨道-土体有限元模型

材料弹性模量/Pa泊松比重度/(kN·m-3)阻尼比钢轨2.1×10110.30076.980.010道床板3.2×10100.30023.500.030底座板3.2×10100.30023.500.030泥岩8.4×1080.33025.900.037砂岩2.69×1090.25224.600.044
轨道-土体模型在靠近激励源的地方单元尺寸取0.65~1.3 m,并在远离激励源的地方逐步增加单元尺寸。本文采用黏弹性边界的三维一致人工边界,即在已建立的模型上向外延伸一层,然后将这一层的外部节点全部约束。轨道结构材料参数为:扣件刚度5×107N/m,阻尼比0.25;道床板与底座板之间设置减震垫,刚度2.5×106N/m,阻尼比0.2;底座板与土体连接处刚度3.97×1010N/m,阻尼比0.2。
2.2 站房结构有限元模型
站房结构尺寸为138 m×69.75 m。站房共3层:第1层为候车大厅和办公室;一楼办公区到屋面之间夹层为第2层;第3层为屋面。站台层到一楼候车大厅高13.9 m,一楼候车大厅到二楼休息区高5.3 m,二楼休息区到屋面层高6.1 m。梁柱采用BEAM188单元模拟,墙面和楼板采用SHELL63单元模拟,有限元模型见图3,具体的材料参数见表2。

图3 站房结构有限元模型
站房结构梁、柱、板的网格尺寸均为0.5 m,站房柱底约束UX、UY、UZ三个方向。
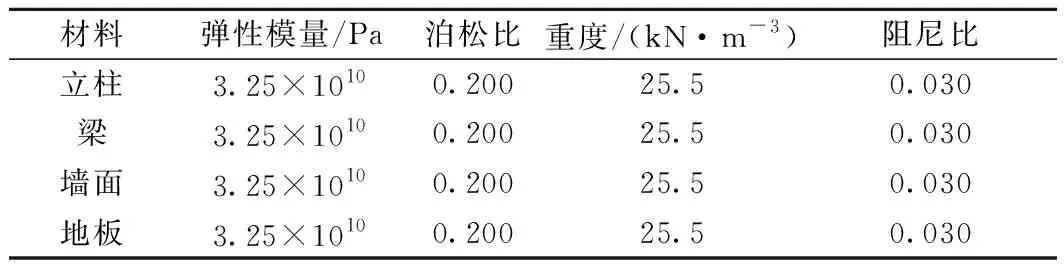
表2 站房有限元模型材料参数
2.3 激励荷载
根据前述车辆-轨道耦合分析模型,推导出频域内的轮轨力计算公式,编制Matlab程序计算出不同车速下的轮轨力,计算中选取ISO轨道不平顺谱,计算公式为[18]
(11)
式中,r0为参考不平顺值,r0=1 μm;λ为不平顺波长,λ=v/f;v为列车速度;f为频率。
车辆动力学参数选取:1/4转向架质量1 000 kg,单个车轮质量800 kg,一系悬挂刚度5×105N/m,一系悬挂阻尼2.25×103N·s/m,二系悬挂刚度1.13×105N/m,二系悬挂阻尼5.02×103N·s/m。通过Matlab计算出的轮轨动态作用力如图4所示。
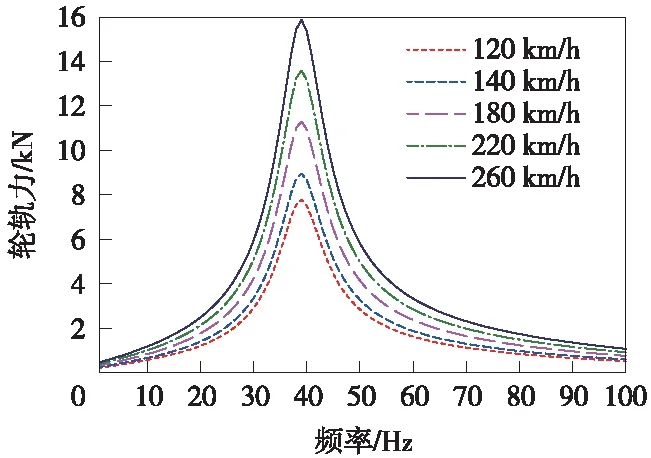
图4 轮轨动态作用力
本文考虑CEH380A型列车,该车全长203 m,含6个动车组和2个拖车组。根据CRH380A的实际情况,将计算得到的轮轨力以荷载列的形式施加到轨道结构上,求解轨道-土体模型的振动响应。
2.4 结果分析
根据上述模型,计算得到了列车以120、140、180、220 km/h通过正线轨道4和轨道5时站台与站房结构的振动响应结果。站房结构前6阶振型均为墙面的局部振动,第7阶振型为站房整体的横向振动,如图5所示。
本文计权曲线采用ISO 2631于1997年颁布的新Z计权曲线,图6给出了1985年颁布的旧Z计权曲线与新Z计权曲线的对比。
2.5 站台振动响应
图7给出了列车以不同速度通过轨道4、5时站台的振动响应,观测点为站台1、站台2、站台3的中心点。从图7可以看出:列车以120 km/h通过轨道4、5时,站台1、站台2、站台3的最大Z计权振动加速度级分别为67.7、69.6、71.3 dB;列车以140 km/h通过轨道4、5时,站台1、站台2、站台3的最大Z计权振动加速度级分别为68.9、70.8、72.5 dB;列车以180 km/h通过轨道4、5时,站台1、站台2、站台3的最大Z计权振动加速度级分别为70.9、72.9、74.5 dB;列车以220 km/h通过轨道4、5时,站台1、站台2、站台3的最大Z计权振动加速度级分别为72.5、74.5、76.1 dB。
从图7可以看出,列车在不同运行速度下,站台振动优势频率(振动响应突出频段范围)为20~63 Hz。在1 ~5 Hz频率范围内,站台1的振动响应最小,站台2与站台3的振动响应接近,站台3的振动响应略大;在5~50 Hz频率范围内,站台1、站台2和站台3的振动响应曲线基本一致;在50~80 Hz范围内,站台3的振动响应最大,站台1和站台2的振动响应接近。站台振动加速度级峰值均出现在40 Hz左右,这一现象可由施加的列车激励源波形图得到解释,列车激励源的峰值出现在40 Hz左右。

图5 站房整体横向振动(第7阶,频率2.2Hz)

图6 新旧Z计权衰减曲线对比

图7 列车以不同速度同时通过轨道4、5时站台的Z计权振级
2.6 站房振动响应
图8给出了列车以不同速度通过轨道4、5时,站房结构Z计权振动加速度级曲线。从图8可以看出:列车以120 km/h通过轨道4、5时,一楼候车大厅、一楼办公室、二楼休息区的最大Z计权振动加速度级分别为68.3、75.9 dB和73.4 dB;列车以140 km/h通过轨道4、5时一楼候车大厅、一楼办公室、二楼休息区的最大Z计权振动加速度级分别为69.6、77.2 dB和74.7 dB;列车以180 km/h通过轨道4、5时一楼候车大厅、一楼办公室、二楼休息区的最大Z计权振动加速度级分别为71.6、79.2 dB和76.7 dB; 列车以220 km/h通过轨道4、5时一楼候车大厅、一楼办公室、二楼休息区的最大Z计权振动加速度级分别为73.2、80.8 dB和78.2 dB。
从图8可以看出,列车不同运行速度下,在1.25~4 Hz范围内,二楼休息区与一楼候车大厅的振动加速度级基本一致,一楼办公室的振动加速度级最小;在4~10 Hz范围内,二楼休息区振动加速度级最大,一楼办公室次之,一楼候车大厅最小;在10~80 Hz范围内一楼办公室与二楼休息区的振动加速度级比较接近,一楼候车大厅的振动加速度级最小。

图8 列车以不同速度同时通过轨道4、5时站房的Z计权振级
3 结论
通过建立车辆-轨道耦合模型、轨道-土体模型和站房结构模型,计算得到了站台站房振动响应规律,主要结论如下。
(1)列车以不同速度通过站台4、5时,站台、站房振动加速度响应规律基本一致,速度仅影响站房、站台振动响应的大小。
(2)站台振动优势频率范围为20~63 Hz,站房振动优势频率为10~60 Hz。列车同时通过轨道4和轨道5时,站台区域,站台3的振动响应最大;站房区域,一楼办公室振动响应最大。
(3)站台与站房振动的峰值频率均集中在40 Hz左右,这与轮轨力的峰值频率一致,采用减振措施时应重点关注40 Hz左右的振动效果。
