改进型解耦自适应复数滤波器锁相环

谢永强 ，朱玉振 ，翟晓超 ，姜 波 ，李 璨

（1.国网山东省电力公司检修公司淄博运维分部，山东 淄博 255000；2.国网山东省电力公司菏泽供电公司，山东 菏泽 274012；3.山东网源电力工程有限公司，山东 济南 250000）

0 引言

电网同步技术是电网中各功率变换器控制系统中的一个重要技术，通过准确检测电网幅值、相位和频率等信息，以达到功率变换器与电网同步工作的目的。锁相环（PLL）作为一种优秀的同步技术，现已被广泛应用于静止无功发生器（D-STATCOM）、有源滤波器（APF）、并网逆变器等功率变换器当中。锁相环技术可以分为两类：开环锁相环与闭环锁相环。开环锁相环如过零检测，通过检测过零点时间来计算相位，因其对电压信号比较敏感，实际应用中，当电压幅值、相位以及频率发生突变时检测效果不佳。现在研究较多的闭环锁相环结构有同步参考坐标系锁相环（SRF-PLL）和静止坐标系锁相环（αβ-PLL）[1]。文献[1]介绍了这两种结构的锁相原理，指出两种结构在理想电网电压情况下可实现准确锁相，但是在非理想情况下，由于三相电网电压通常会出现电压跌落、频率突变、相位突变以及谐波等问题，上述方法无法准确锁相；为抑制电网电压中的负序分量和谐波成分，文献[2-3]分别在上述SRF-PLL的基础上加入低通滤波器、陷波器，但这无疑大大影响了其动态性能。文献[4]提出了一种延时T／4（T为工频周期）构建正交信号实现序分解的方法，但是当频率发生波动时，无法准确分离正负序分量，检测误差很大；文献[5]提出了一种基于复数滤波器矩阵正交信号发生器（Orthogonal Signal Generator，OSG）的锁相方法，通过使用复数滤波器矩阵构建正交信号发生器实现正序基波分量的提取，从而实现了准确锁相；文献[6]提出了一种基于双同步坐标变换解耦（DecoupledDoubleSynchronousReferenceFrame PLL，DDSRF-PLL）的方法，虽然该方法通过解耦网络消除了负序分量的影响，但易受低次谐波的影响，对滤波环节要求更高。

本文在分析当前锁相环研究热点问题的基础上，以提取正序基波分量为核心问题，选择静止坐标系锁相环作为基本锁相结构，提出了一种基于自适应复数滤波器解耦的改进型锁相环方法。该方法引入具有极性选择性的正、负序一阶复数滤波器构建解耦网络，通过改进滤波结构、合理选择其参数，实现了在αβ坐标系下正序基波电压的准确提取。

1 静止坐标系锁相环（αβ-PLL）基本原理

电网三相电压us=[usausbusc]T，经过 Clarke 变换以及Park变换可得两相同步参考坐标系下电压分量us=[usdusq]T。该变换过程如式（1）、式（2）所示。

理想情况下，电网电压为三相对称电压，可以表示为

静止坐标系锁相环（αβ-PLL）无须经过Park变换，在αβ静止坐标系就可以实现相位的精确锁定，其结构如图1所示。

图1 静止坐标系锁相环结构

2 改进的锁相环

图2为改进的基于自适应复数滤波器锁相环。其中，三相电网电压 usa、usb、usc经过 Clarke变换得到αβ坐标系下的分量usα、usβ，然后经过一个交叉解耦自适应复数滤波后，再次经过一个一阶正序复数滤波器后得到最后将输入到静止坐标系锁相环中进行锁相。

图2 改进的锁相环

2.1 电网电压分析

考虑基波跟各次谐波分量，忽略零序分量，在三相坐标系下，三相电网电压可以表示为

式（5）对应在αβ坐标系下的表达式为

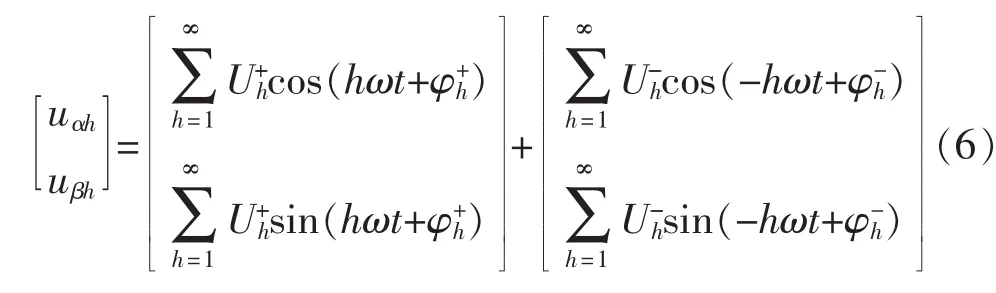
由式（6）可知，Clarke变换前后电网电压次数不会发生改变，锁相环锁定的是电网中基波正序电压的相位，只需要构建具有正负序解耦加滤波功能的结构即可提取基波正序电压。

2.2 复数滤波器分析

为实现基波正序电压的提取，在Clarke变换后加入了滤波环节。同时为实现正负序分离，本文引入了具有极性选择性的一阶复数滤波器，式（7）为一阶正序复数滤波器，式（8）为一阶负序复数滤波器。

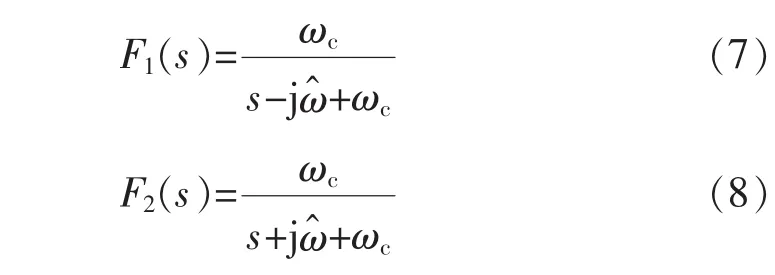
一阶正序复数滤波器的幅频特性、相频特性分别为

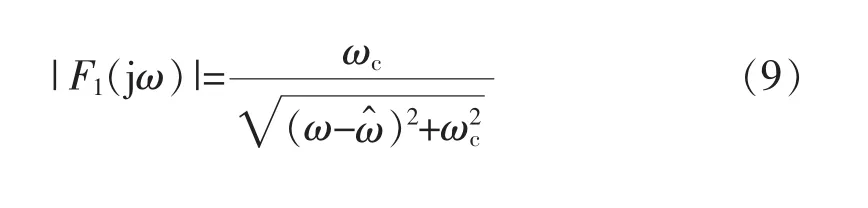
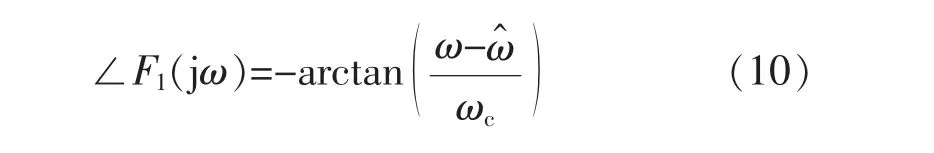
由频率特性可以看出，三相电网电压经过一阶正序复数滤波器后，基波正序分量（频率为）可以无衰减零相移的通过，随着频率远离，信号幅值会出现衰减；但是基波负序分量（频率为-）经过一阶正序复数滤波器后幅值为相移为同理，对于一阶负序复数滤波器，基波负序分量可以无衰减零相移的通过，但基波正序分量会出现衰减，并未完全滤除。

图3 一阶正序复数滤波器波特图

2.3 自适应复数滤波解耦模块分析

图4为复数滤波器解耦模块。其复频域数学模型为

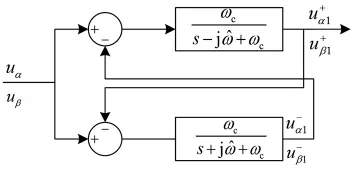
图4 基于复数滤波器的解耦模块

由式（11）得到该自适应复数滤波器解耦模块的时域数学模型为

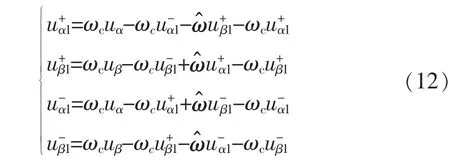
式（12）可以写成

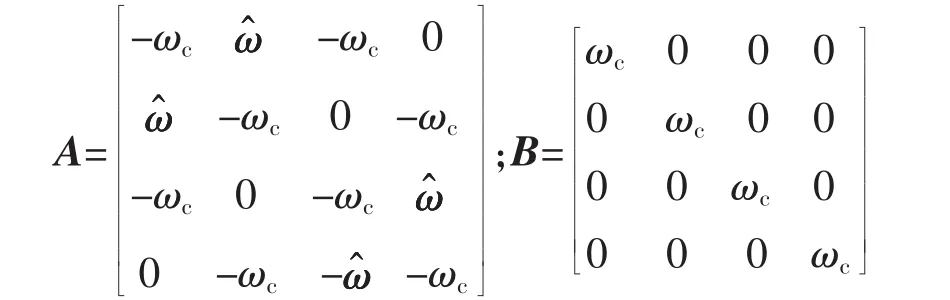
由控制理论可知，非齐次状态方程（13）的解为

式中：eA·（t－t0）x（t0）为稳态分量；为暂态分量。由文献[8]可知，当输入电压只含基波分量时，对于稳态分量有

PET/CT采用美国GE公司生产的Discovery-16CT和minitrace回旋加速器，18F-FDG由Tracerlab FXFN合成器完成，FDG的放化纯度＞95%。所有病人在检查前禁止吸烟、饮酒及咖啡，并禁止输注含葡萄糖的药物，禁食4-6h，空腹血糖控制在5.1-10.0mmol/L。经患者腕部或者肘部静脉注射18F-FDG，休息1个小时后进行PET/CT成像。根据结节大小及结节形态分为：A型结节 （结节直径＜1cm），B 型结节（结节直径 1cm≤直径＜2cm），C型结节（结节直径2cm≤直径＜3cm）。

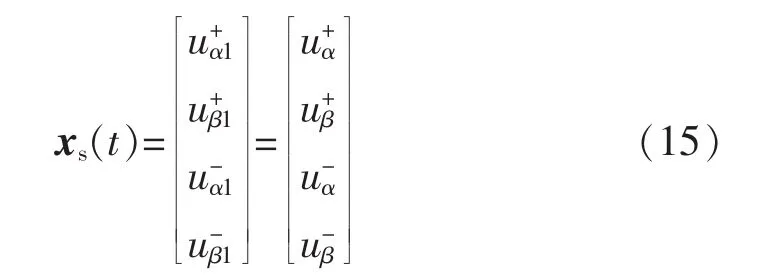
式 （15）说明对于输入只含基波的三相电网电压，上述结构可以实现正负序电压的解耦。然而，经过仿真验证，当电网中含有谐波时，上述结构的滤波能力并不能有效地达到国家标准。因此考虑在上述结构后面增添一阶正序复数滤波器的方式，进一步滤除谐波分量，改进结构如图5所示。

图5 改进型复数滤波器的解耦模块

其数学模型为

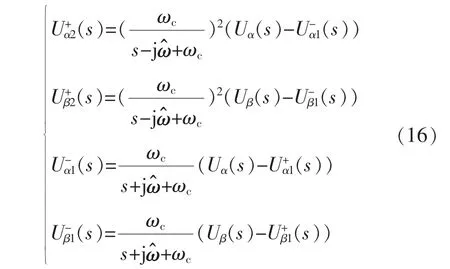
已经分析上述结构的正负序解耦能力，下述分析其滤波能力。

由式（11）可以求得Uα（s）到以及Uβ（s）到的传递函数

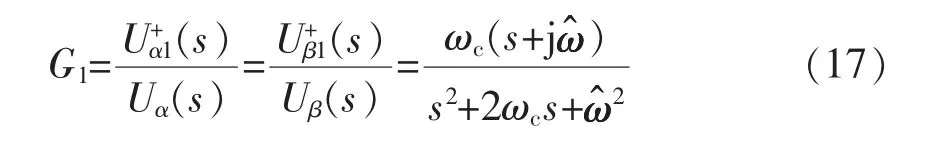
由式（16）可以求得Uα（s）到以及Uβ（s）到的传递函数

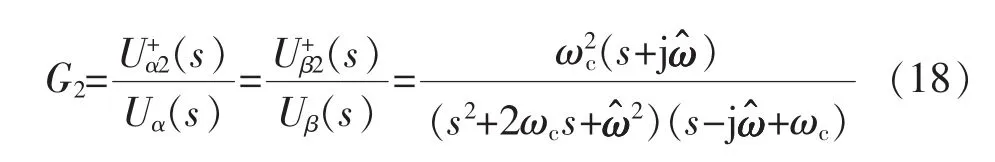
图 6 为在ω^＝314 rad／s时，G1与G2的波特图。

图6 G1与G2的波特图

图6中，G1为自适应复数滤波器解耦模块的频率特性，G2为改进自适应复数滤波器解耦模块的频率特性。由幅相频特性曲线可以看出前者跟后者在ωc=314 rad／s处增益均为1且相移为0，但是随着频率远离ω^，后者幅值衰减速度较前者快很多，即后者的选频效果远优于前者。

由上述分析可知，在电网电压频率确定时，改进的复数滤波结构可以实现正负序信号精确分离，同时可以有效地滤除谐波信号。然而实际电网应用中常出现频率波动，必然会影响上述复数滤波结构的选频性能[9-13]。为了减小频率波动带来的误差，需要对滤波器的参数进行调整，通过将实时锁定的频率反馈至复数滤波器作为选频频率，实现频率自适应调整，如图2虚线框所示。

3 自适应复数滤波器参数设计

由上文分析可知ωc决定了自适应复数滤波器解耦模块的动态性能，为了实现较好的动态选频效果，需要先对ωc进行整定设计。

通过观察传递函数的分母特征根轨迹可以对系统的动态性能以及稳定性进行评估分析：由自动控制原理可知，为使系统保持稳定，根轨迹需分布在s域左半平面；主导特征根距离虚轴越远，则系统动态响应速度越快。当ω^=314 rad／s时，可以得到参数ωc在不同取值下的特征根的分布情况如图7所示。

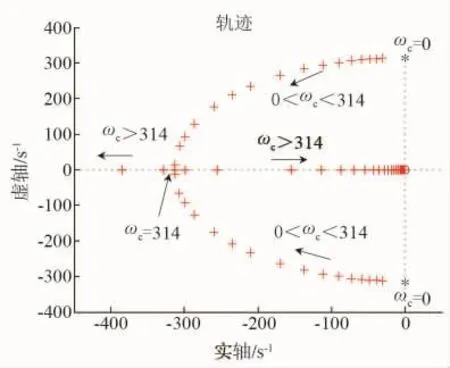
图7 主导特征值分布

由图7可知当ωc＞0时，根轨迹均在s域左半平面，说明系统是稳定的。当ωc由0变化至314 rad／s过程中时，主导特征根向远离虚轴方向移动，系统动态响应速度加快；当ωc由314 rad／s增大时，主导特征根向靠近虚轴方向移动，系统动态响应速度减慢。故综合考虑系统的选频性能与稳定性，选取ωc=314 rad ／s。

4 仿真分析

为了检验所提出改进型基于自适应复数滤波器锁相环的性能，采用Matlab／Simulink进行仿真。仿真参数为：电网电压幅值为220 V，频率为50 Hz；复数滤波器截止频率ωc为 314 rad／s；PI控制器参数 Kp为 75，Ki为 200。

利用所提出方法在电压跌落、频率突变、相位突变以及注入谐波等环境下进行仿真，并分析其动态性能与稳态性能。

4.1 三相电压不对称

此种情况选择输入电压暂降作为不平衡情况。设置故障前三相电压对称，即0.08～0.10 s时，ua=220∠0°V；0.10～0.20 s时，a 相电压跌落为 0，如图 8（a）所示。

由图8可以看出，当出现电压暂降时，由于三相电压不再对称，uα、uβ也不再正交对称，如图 8（b）所示，本文所提方法仅仅用了一个工频周期就可以准确快速的提取其正序基波分量如图 8 （c）所示。图8（d）给出了传统SRF-PLL、解耦双同步坐标变换PLL以及本文提出的改进型解耦自适应复数滤波器PLL锁频性能的对比图，可以看出传统SRFPLL锁频结果存在严重的波动分量，而后两种方法只需用1个工频周期就可以准确检测出电网频率。

4.2 电网电压对称时频率突变

此种情况选择输入电压频率突变作为不平衡情况。设置故障前三相电压对称，即0.08～0.10 s时，ua=220∠0°V；0.10～0.20s时，a相电压频率由 50Hz突变到50.5 Hz，如图9所示。

由图9可以看出，当电压出现频率突变故障时，本文方法可以准确提取正序基波分量，由图9（d）可以看出，当电压出现频率突变故障时，本文所提方法相比于传统SRF-PLL、解耦双同步坐标变换PLL锁频精度更高、动态响应速度更快，只需用1个工频周期就可以准确检测出电网频率为50.5Hz，传统SRF-PLL存在精度低而解耦双同步坐标换PLL存在动态响应速度慢的缺点。

图8 电压跌落时仿真结果

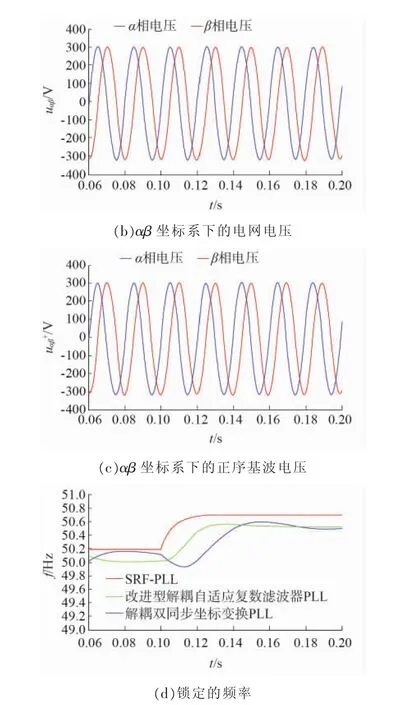
图9 电压频率突变时仿真结果

4.3 电网电压对称时相位突变

此种情况选择输入电压相位突变作为不平衡情况。设置故障前三相电压对称，即0.08～0.10 s时，ua=220∠0°V；0.10～0.20 s时， 三相电压相位突变60°，如图 10（a）所示。

由图10可以看出，当电压出现相位突变故障时，本文所提方法仅仅用了一个工频周期就可以准确快速的提取其正序基波分量如图 10（c）所示。图10（d）给出了传统SRF-PLL、解耦双同步坐标变换PLL以及本文提出的改进型解耦自适应复数滤波器PLL锁频性能的对比图，可以看出三种锁相方法经过一定时间调整均可以准确锁定频率，但是动态响应速度大小为：SRF-PLL＞改进型解耦自适应复数滤波器PLL＞解耦双同步坐标变换PLL。

图10 电压相位突变时仿真结果

4.4 电网电压对称时注入谐波

此种情况选择注入谐波作为不平衡情况。设置故障前三相电压对称，即0.08～0.10s时，ua=220∠0°V；0.10～0.20 s时，a相电压注入10%的5次正序谐波分量，b相电压注入10%的3次负序谐波分量如图11（a）所示。

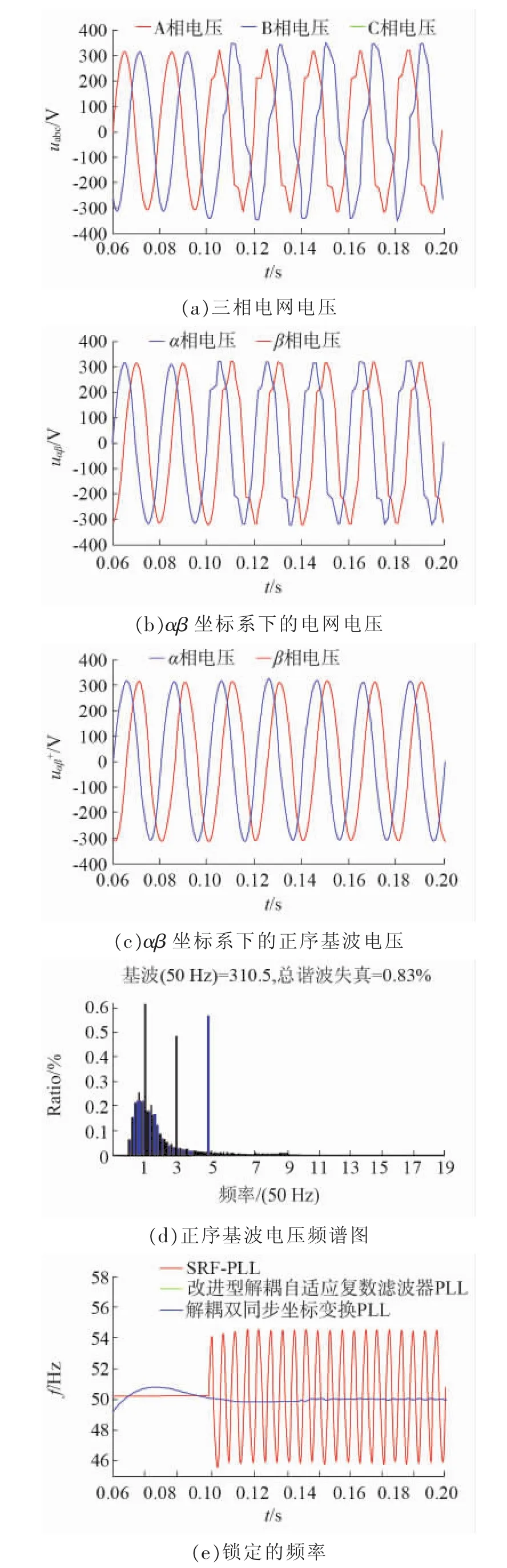
图11 注入谐波时仿真结果

由图11（c）可以看出，当电压出现大量谐波时，本文方法可以实时准确提取正序基波分量图11（d）为所提取正序基波信号的傅里叶分析频谱图，不难发现其中谐波含量为0.83%，远低于相关要求。同时经过一个工频周期，电网频率就被锁定进入稳态，锁相频率偏差为符合国家要求。

5 结语

首先介绍了静止坐标系锁相环（αβ-PLL）的基本结构，分析了静止坐标系锁相环工作的基本原理。同时，提出一种自适应复数滤波解耦模块，实现频率自适应滤波和正序分量提取功能。仿真结果表明，采用将静止坐标系锁相环与自适应复数滤波解耦模块结合起来的方法，可以在各种不平衡工况环境下实现基波正序分量以及电网频率的准确快速提取和锁定。与传统锁相方法相比，该方法无需对称分量法以及大量的坐标变换，具有算法简单、易于实现等特点。