基于改进电导增量法的光伏电池最大功率点跟踪研究
2018-07-27孙洪伟贾明娜咸日常
孙洪伟,贾明娜 ,王 玮 ,咸日常
(1.山东理工大学,山东 淄博 255049;2.山东科汇电力自动化有限公司,山东 淄博 255087)
0 引言
太阳能光伏发电凭借其绿色环保无污染的特点,近年来逐渐受到各国的重视并发展迅速。现有的光伏发电系统一直存在效率低下的问题,这也成为制约光伏发电系统发展的技术瓶颈[1]。
目前,解决光伏发电的效率转换问题主要采用带有最大功率点跟踪(MPPT,Maximum Power Point Tracking)功能的控制器的方法,通过对光伏最大功率的跟踪,可在现有光伏阵列的基础上,充分提高光伏阵列的转换效率,因此对光伏最大功率的跟踪也是光伏系统研究的重要方向。
最大功率点跟踪方法主要有扰动观测法、电导增量法、短路电流法等,由于这些算法均为单模算法,且自身存在固有不足,使得其实际应用效果不明显。近年来出现了利用两种单模算法结合的双模控制算法,其中的非对称模糊PID控制策略[2],提高了在最大功率点处的稳态特性,但其稳态模糊表需要经验来确定;基于滑模技术的最大功率点跟踪控制方法[3],解决了光伏电池初始阶段跟踪速度慢的缺点,但是存在稳态时仍有震荡的缺点;基于单周控制理论的最大功率点跟踪方法[4],虽可通过纯模拟器件实现,但是参数选择困难,使其工作点并非真正的最大功率点。
针对以上问题,提出了一种改进的电导增量法,该方法通过改进传统电导增量法中的步长因子,有效解决了传统电导增量法中存在的跟踪速度慢、稳态时振荡幅度大的问题。实验表明,与传统的电导增量法相比,改进后的电导增量法能够提高光伏电池的动态性和稳态性,从而提高其转换效率。
1 光伏电池原理
1.1 光伏电池原理分析
图1为光伏电池的等效电路[5],太阳能电池主要由半导体硅制成,半导体在光照条件下吸收光能,激发出电子和空穴,从而半导体中有电流流过,即“光生伏特效应”。
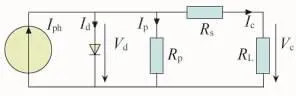
图1 光伏电池等效电路
图1中,Iph为光电流,Id为二极管电流,Ip为并联电流,Rs为串联电阻,Rp为并联电阻,RL为负载阻抗,Vd为二极管电压,Vc和Ic分别为输出电压和输出电流,光伏电池的输出电流表达式为[6-7]
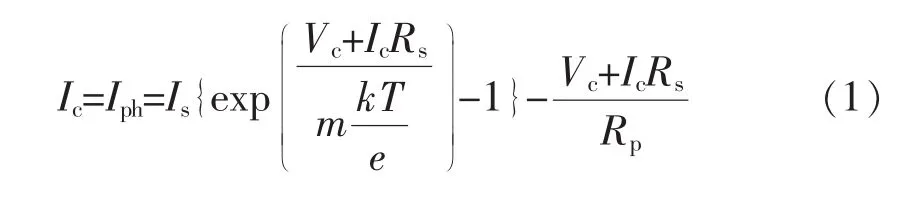
相应的光伏电池输出功率为
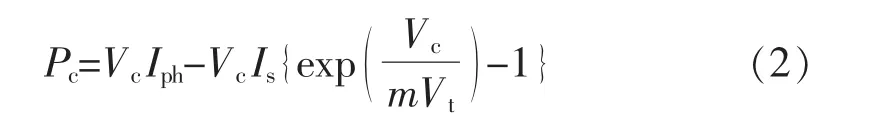
式中:Vc和Ic分别为输出电压和输出电流;Iph为光电流;Is为饱和电流;Vt为温度电压;k为玻尔兹曼常数;e为单位电荷;m为二极管因数。
当光照和温度处于非标准状态下时,可用以下参数来描述光伏电池[8-9]:

式中:Sb为标准光照强度参考 值,Sb=1 000 W/m2;Tb为标准电池温度参考值,Tb=25℃;S为实际光强;T 为实际温度;ΔS=S-Sb;ΔT=T-Tb;a、b、c 为补偿系数。
1.2 光伏电池输出特性分析
在实际应用中,当受到太阳光照和环境温度实时变化的影响,光伏电池的输出特性曲线会发生变化,具有很大的波动性。 根据公式(3)~(6),在 Simulink上搭建数学模型进行仿真,如图2所示。设置其基本参数为 Um=17.7 V,Im=7.94 A,Uoc=22 V,Ise=8.58 A,仿真时补偿系数设置为a=0.002 5,b=0.5,c=0.002 88。
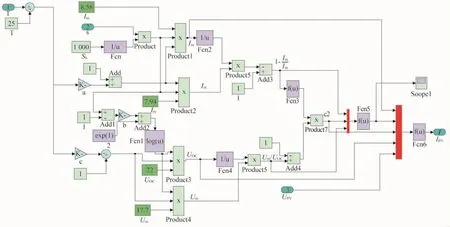
图2 光伏电池仿真模型
在光强为800 W/m2,温度为25℃时,求得光伏电池的输出电压和输出电流、输出功率之间的关系,如图3所示。

图3 光伏电池I—U和P—U曲线
从图3可以看出,光伏电池在低电压阶段类似于电流源,可以认为电流恒定,但在之后电流急剧下降;输出功率随着电压的增加先增大后减小,存在一个最大值,该点为光伏电池的最大功率点,之后功率急剧下降,逐渐趋为0。
为了更好地观察光伏电池的输出功率曲线,在仿真过程中设置了不同的环境变量,通过对比输出功率的变化来分析环境变量对光伏电池的影响。设置温度为25℃并保持不变,分别设置光照强度为600 W /m2,700 W /m2,800 W /m2,得到光伏电池在同一温度、不同光照强度下的输出特性曲线;设置光照强度为1 000并保持不变,分别设置环境温度为15℃、30℃和45℃,得出光伏电池在同一光照强度、不同温度下的输出特性曲线,如图4和图5所示。

图4 同一温度、不同光照强度下特性曲线

图5 同一光照强度、不同温度下特性曲线
由图4~5可知,在温度不变时,光伏电池的输出功率最大值随着光照强度的增加而增加,光照越强,输出功率越高;在光照强度不变时,光伏电池输出功率的上升速度随着光照强度的增加而加快,但是光伏电池的输出功率最大值随着温度的增加而降低,这就要求光伏电池在使用过程中必须有足够光照,同时注意通风降温。
2 电导增量法最大功率点跟踪原理
2.1 传统电导增量法
在传统的最大功率跟踪方法中,电导增量法的跟踪准确性最高,效果最好,是目前较为常用的方法之一。由图3知,光伏电池的P—U曲线为一条单峰曲线,在最大功率点处满足且存在如下判据:

由此可知,当输出电导的变化量等于输出电导的负值时,光伏电池处于最大功率点。
利用Buck-Boost电路调整负载端输出电压,根据跟踪得到的光伏电池输出的最大功率点算出光伏电池的输出电压U,然后根据算出负载端的输出电压,其中α为占空比,Buck-Boost电路原理如图 6 所示[10]。
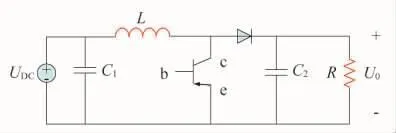
图6 Buck-Boost电路图
为了分析步长D对跟踪速度和稳态时的震荡幅度的影响,在仿真过程中设置两个不同的步长,分别为D=0.01和D=0.001,经仿真得出图 7,其中曲线1为ΔD=0.01时的输出曲线,曲线2为ΔD=0.001时的输出曲线。
曲线1上升速度快,但在稳态时震荡幅度较大,曲线2上升速度慢,但是在稳态时震荡幅度小。
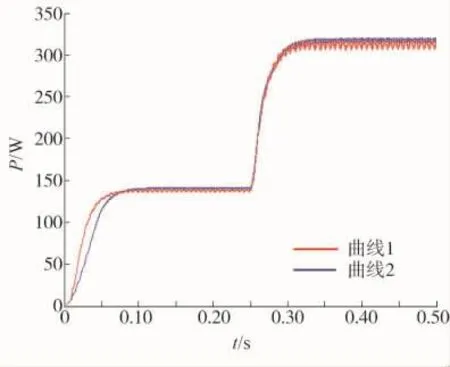
图7 不同步长下的功率输出曲线
由此可知,较大的步长有利于跟踪速度的提升,但是在稳态时震荡幅度较大;较小的步长在稳态时的震荡幅度较小,但跟踪速度较慢。
3 改进型电导增量法
3.1 改进型电导增量法的原理
传统电导增量法的不足是过小的步长会使系统的动态响应较差,而过大的步长则会使系统的稳定性较差。因此,在此基础上提出了一种新的步长因子表达式,由此达到根据光伏电池P—U曲线的斜率而自动改变步长大小的目的。由图3可知,光伏电池的P—U曲线在线性区内近似呈直线,其斜率近似不变;越靠近最大功率点,曲线斜率越小;当达到最大功率点时,其斜率降为0。根据这一特点,设置斜率阈值k1,当光伏电池的P—U曲线的斜率k>k1时,即为阶段1,可认为该阶段为线性区;当光伏电池的P—U曲线的斜率k<k1时,即为阶段2。其中,可以根据不同型号光伏电池的输出曲线来确定k1的数值。
改进型电导增量法即要实现在阶段1的线性区内采用较大的步长以提高跟踪速度;而在靠近最大功率点时的阶段2采用较小的步长,并根据P—U曲线的斜率大小而变化,以减小振动幅度,如图8所示。
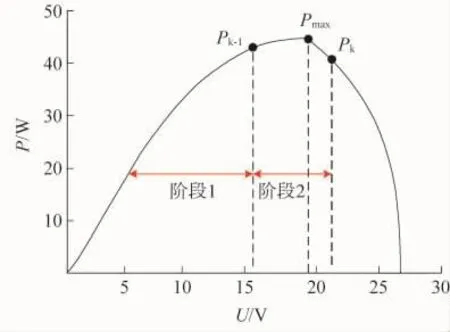
图8 步长变化曲线
传统的变步长电导增量法的步长表达式为

改进型的变步长电导增量法的步长表达式为
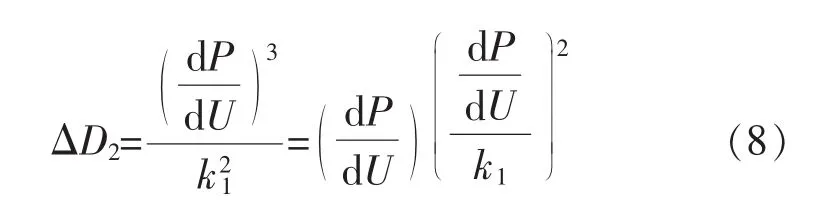
式中:k1为选取的阈值。
3.2 改进型电导增量法步长变化量的变化
如图9所示,曲线1为改进之前的步长变化量,曲线2为改进后的步长变化量,可以看出改进型的步长变化量在光伏特性曲线线性区比改进之前的步长变化量大,改进型步长变化量在接近最大功率点时比改进之前的步长变化量小。利用这样的特点,可以确保改进型MPPT控制器在初期可以快速跟踪光照的变化,在接近光伏电池功率最大点时能够有较小的振荡,克服了传统MPPT的缺点,实现了较好的动态性和稳定性。
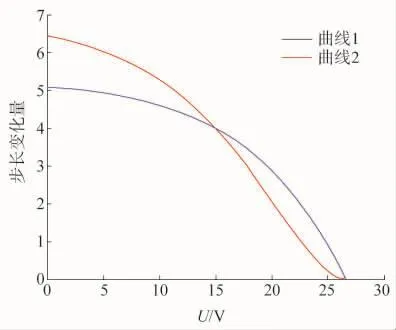
图9 步长因子随输出电压的变化曲线
3.3 改进型电导增量法跟踪效果测试
在MATLAB上搭建光伏系统模型,如图10所示。光伏电池的基本参数为Um=34.8 V,Im=7.47 A,Uoc=44 V,Ise=8.09 A。仿真时补偿系数设置为 a=0.002 5,b=0.5,c=0.002 88。在仿真过程中设置光照强度在 0.1s从 400W/m2跃变为 600W/m2,在 0.25 s 时又跃变为1000W/m2,在温度T=25℃并保持不变及其他环境条件不变的情况下验证传统变步长电导增量法和改进型电导增量法的跟踪效果,如图11~12所示。
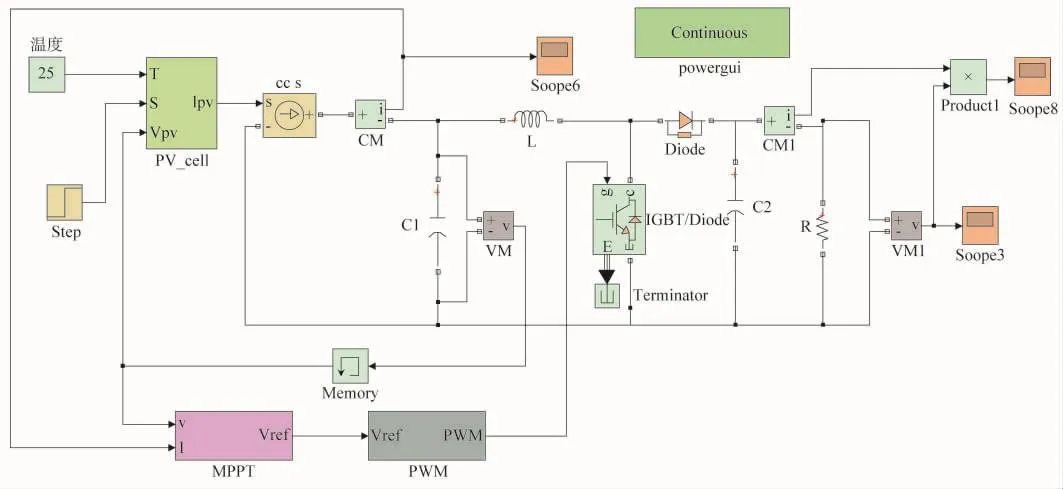
图10 光伏系统仿真模型
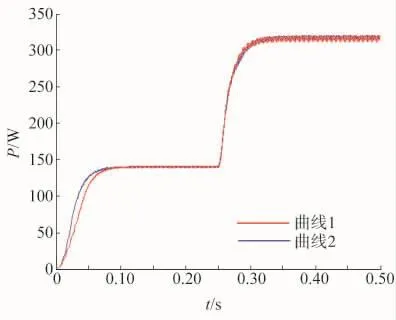
图11 改进算法的功率跟踪仿真
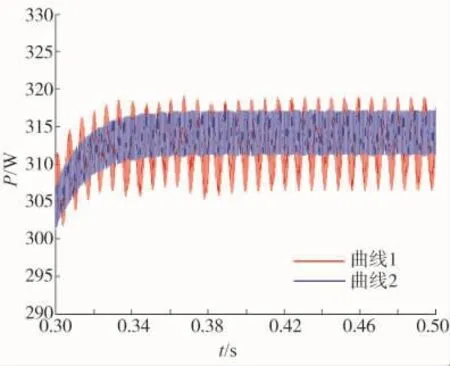
图12 功率跟踪仿真局部放大
图11中的曲线1为传统MPPT功率输出曲线,曲线2为改进后的功率输出曲线。通过对比可以看出改进后的跟踪效果较改进之前有明显的进步。首先,跟踪速度明显提升,可以看出曲线2的上升速度明显快于曲线1;其次,从图12可以看出,稳态时震荡幅度较小,可以看出曲线2在稳态时的震荡幅度明显小于曲线1。这说明改进后的变步长电导增量法具有较快的跟踪速度和较高的稳态精度。
4 结语
根据光伏电池的Simulink模型研究了光伏电池的输出特性曲线,针对传统MPPT步长存在的不足,提出了一种改进的最大功率点跟踪步长表达式。实验表明,与传统的最大功率点跟踪策略相比,该方法具有初始阶段跟踪速度快,稳态阶段震荡幅度小的优点。
