小波分析在电力负荷数据处理中的应用

李雨轩，高 鹏，赵庆磊

（国网山东省电力公司检修公司，山东 济南 250118）

0 引言

小波分析（Wavelets Analysis）是 20世纪 80年代后逐步兴起和发展的一种新的数学分析方法。它作为数学学科的一个分支，汲取了现代分析学中泛函分析、数值分析、傅里叶分析、调和分析等众多分支中的精华，具有深刻的理论意义［1］，在信号处理、故障诊断、状态监视、语音识别、刑事侦破等十几个学科领域得到了广泛应用［2］。

自1822年傅里叶（Fourier）发表“热传导解析理论”以来，傅里叶变换一直是数学分析领域中最完美、应用最广泛、效果最好的一种分析手段。但傅里叶变换只是一种纯频域的分析方法，需要利用信号的全部时域信息，这是一种整体变换，缺少时域定位功能［3］。而小波变换是一种时间—尺度（时间—频率）分析方法，它具有多分辨率分析的特点，而且在时频两域都具有表征信号局部特征的能力，很适合探测正常信号中夹带的瞬变反常信号并能够分析其成分，所以被称为“数学显微镜”［4］。

电力负荷数据是电网公司采集的反映电力用户用电情况的时间序列。将电力负荷数据看成是一种大时间粒度的数字信号，利用小波分析对其进行去噪和压缩，极大地方便了电力负荷数据的处理工作，具有很高的应用价值。

1 小波分析原理

1.1 连续小波和离散小波

函数 f（t）的连续小波变换为

式中：Ψ（x）∈L2（R）为小波函数；a 为尺度因子；b 为平移因子。

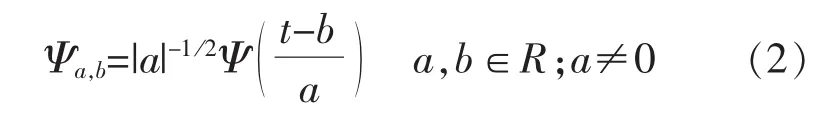
相应的重构公式为

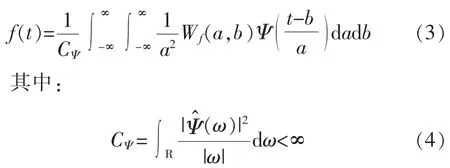
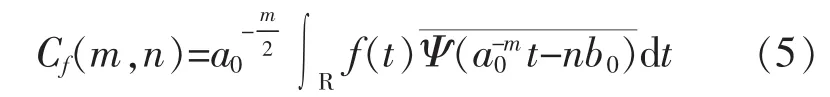
1.2 Mallat塔式算法

小波变换在映射到计算域时存在信息冗余，计算量很大［5］。为此，基于多分辨率分析理论的Mallat塔式算法应运而生。

数学上可以证明：

逆运算为：

式（9）即 Mallat塔式分解算法，式（10）为 Mallat算法的重构算法，如图1所示。

图1 Mallat塔式算法分解和重构

图1中，Cj和Dj为2j分辨率下的离散逼近和离散细节，分别对应信号的低频成分和高频成分。

1.3 小波系的选择

小波函数不是唯一存在的，常见小波有Haar小波、Daubechies（dbN）小波系、双正交小波系、Coiflet小波系等。处理电力负荷数据选择的小波基至少要满足条件：1）必须是紧支撑的，且支撑区间要小，这样有利于奇异点的检测。2）能够灵活的调整分辨率，因为不同类型的负荷数据拥有不同的时间粒度。dbN小波系满足这两个条件，因此选用该小波系进行分析。

2 小波分析在负荷数据去噪中的应用

2.1 噪声来源

电力负荷数据作为一种特殊的数字信号，在采集和传输过程中会掺杂进各种噪声，其噪声来源主要有：1）负荷数据的坏点。由于人为失误或系统故障，数据出现坏点和缺失，在负荷曲线上表现为奇异点。2）系数的放大效应。原始负荷数据通常需要乘以一个大的系数才是真实数据，因此任何细小的干扰都可能被放大形成较大的波动。3）负荷本身的不稳定性。这种不稳定性会在负荷曲线上形成无数小的毛刺。在一些强调宏观性和整体性的应用场合，这些细节意义不大，也将其视为一种噪声。

电力负荷数据中的噪声如不滤除，会严重干扰电网公司的决策。采用传统的office软件筛选耗时耗力，因此利用小波分析滤除负噪声意义重大。

2.2 小波去噪方法

去噪的基本目的就是减少噪声部分的幅值，使去噪后的信号尽可能地逼近原始信号［6］。目前，小波去噪的主流方法主要有模极大值去噪法［7］和阈值去噪法［8-10］。其中，阈值去噪法计算简单，速度快，且在最小均方误差意义下可达到近似最优［11］，因此选用阈值去噪法。

Mallat塔式算法可逐层将信号分解为逼近和细节成分，而噪声主要隐藏在细节成分中。信号去噪就是有选择性的滤除一些细节系数，则重构后的信号就会接近于原始信号。

2.3 阈值选择策略

细节系数中除包含噪声外，还构成了信号重要的细节特征，因此不能将其全部滤除。噪声强度σ估计为

式中：dj（n）为第j层小波系数；N为该层小波系数的个数；δ为经验系数。

则通用阈值T可表示为

本文提出双层阈值法，首先将大于T1的系数收缩进T1范围内，然后重新估算噪声形成T2，利用T2对上一步信号进行软阈值处理，其取值函数为：

第一步

第二步

由于奇异点产生的小波系数往往远大于通用阈值，而传统的软阈值法只是将大于阈值的系数收缩一次，因此并不能有效地去除奇异点。而通过设置双层阈值，首先将奇异点系数进行多次收缩，使其回归正常范围内，再对全局信号进行软阈值处理，可以较好地解决奇异点问题。

2.4 案例分析

图2为某大型商场2012—2016年的单日最大负荷曲线。单日最大负荷可以近似代表一个用户的负荷水平，在电网规划中占有重要地位。由图可知，此曲线的噪声由两部分组成：1）数据坏点（奇异点）；2）负荷不稳定而形成的毛刺。

图2 某大型商场单日最大负荷曲线

将此曲线用db5小波做5层分解，得到细节系数分布如图3所示。由图3可知，前3层分解系数均含有较为明显的奇异点和高频噪声。估算其噪声强度，δ分别取0.5和1.5形成双层阈值，按照双层阈值策略处理细节系数，保留全部逼近系数，重构后如图4所示。其中S1和S2分别为双层系数处理的结果，S3为使用传统软阈值法的处理结果。

图3 负荷曲线细节系数分布

图4 负荷曲线去噪结果

由图2、图4可知：1）S1相较于S已经消除了数据奇异点，非奇异点处的数据与原数据有很高的相似度；2）S2变得更加平滑，更能反映负荷特性和一般趋势；3）S3虽然较原始曲线更加平滑，但并未有效去除奇异点。综上说明双层阈值法可以有效地去除数据中的奇异点和噪声，相较于传统软阈值法优势明显。

为评价此方法误差水平，定义衡量指标：平均绝对误差为β，平均相对误差为η，赋范均方误差为βnorm。

误差统计如表1所示。由表1可知，S2、S1、S3曲线误差逐渐减小且三者误差都处于较低水平。考虑到S1和S2消除了奇异点造成的误差增大，其真实误差应低于此水平，说明此方法能够较好地控制误差。实际操作中，可根据不同的精确度要求灵活的调整通用阈值，阈值越小，则细节越少，去噪后曲线也越光滑，但误差也越大。

表1 去噪结果误差表

3 小波分析在负荷数据压缩中的应用

电网公司每时每刻都在生成各种负荷数据，这会占用大量的存储空间，同时增加数据管理成本，因此有必要对负荷数据进行压缩。

3.1 小波压缩方法

小波分解后逼近和细节系数的总个数与原信号的采样点个数相同，而时间序列的能量和宏观性质是由逼近系数和大幅值的细节系数决定，因此舍去部分小幅值的细节系数，再利用特殊的编码方式记录没有被舍去的细节系数的位置，就可以到达只存储少量小波系数而重构原始时间序列的目的，从而实现对数据的压缩。

3.2 阈值选择策略

小波细节系数的取舍同样需要用到阈值，但压缩阈值没有统一的估算方法。本文选用的阈值表示为

式中：j为当前分解层数；N为该层小波系数的个数；A∈（0，1）命名为压缩系数，其取值由压缩率决定。

则细节系数的取值函数为

3.3 案例分析

如图5所示为某商业街一周内的负荷曲线，采样频率为1 min，共10 080个采样点。

图5 某商业街周负荷曲线

将此负荷曲线用db5小波做3层分解，压缩系数分别设为0.1、0.3、0.6，压缩后结果如图6所示。

图6 压缩后负荷曲线

由图 6 可知，S′1、S′2、S′3 均与原负荷曲线有较高的相似度，说明重构效果较好，而它们参与重构的系数分别只有3 641、1 857、1 320个，相较于原始信号的10 080个，均有大幅度减少。

定义压缩比为：

式中：N*为压缩后小波系数的个数；N为原始信号的采样点个数。

误差衡量指标同前文所定义，则压缩比和误差如表2所示。由表2可知：1）压缩比越小，压缩效果越好，但误差也越大；2）即使达到了13.1%的压缩比，其误差仍然处于较低的水平。所以此方法能仅损失较少的曲线细节，使负荷数据得到极大的压缩，从而成倍的提高存储介质的利用率。实际操作中可以通过调整压缩系数和分解层数灵活的改变压缩比。

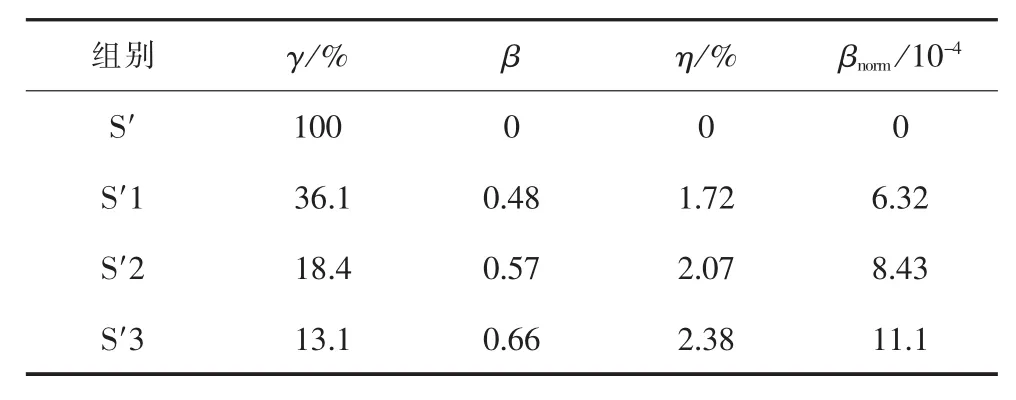
表2 压缩结果评价表

4 结语

小波分析是数字信号处理的支柱理论之一，本文将其应用领域扩展到电力负荷数据的处理中，并提出了双层阈值方法。实际案例分析表明，小波分析应用于负荷数据去噪时，能够有效地去除奇异点和噪声，极大节约了人力和时间成本；而应用于负荷数据压缩时，可以在较小的误差水平下，获得很好的压缩效果，从而成倍减少数据占用的存储空间。因此小波分析在电力负荷数据处理方面具有很高的应用价值。