基于D-S证据理论的中长期电力负荷组合预测

赵延文

（国网山东省电力公司东营供电公司，山东 东营 257091）

0 引言

中长期电力负荷预测作为电网规划中极为重要的一环［1-2］，其预测精度的高低将直接决定电网规划的质量及水平。电力负荷预测经过四十多年的研究发展，提出了很多卓有成效的预测方法及模型，并在实际中得到了广泛应用。

早期的负荷预测研究主要是基于数理统计，通过分析负荷与各种因素存在的关系，建立负荷的统计模型，然后根据模型对负荷进行预测。这其中典型的代表主要为回归分析法及时间序列法。回归分析作为一种比较成熟的电力负荷中长期预测方法，已经在中长期负荷预测领域得到了广泛的应用［3-5］。而时间序列法基于负荷变动时间上的延续性，在短期负荷预测领域中得到了非常广泛的应用［6-7］。

尽管建立统计模型进行预测计算量较小且速度较快，但随着电力系统结构的不断扩大，这种方式已经不能满足电网规划的精度要求。随着人工智能的深入研究发展，领域内专家及学者逐渐将负荷预测转移到与人工智能相结合的方向上来。文献［8］将神经网络应用于电力中期负荷预测中，取得了较好的效果；文献［9］以马尔科夫链修正为基础，对电力中长期负荷进行了预测；文献［10］将小波理论与神经网络进行结合，对中长期负荷进行了预测；文献［11-12］将改进后的灰色系统理论模型应用于电力负荷的中长期预测中，验证了模型的可行性。文献［13］针对负荷变化的不同阶段建立了差异化的灰色理论模型，对电力中长期负荷预测进行了研究。

为了提高中长期负荷预测的精度，本文首先分别应用回归分析法及灰色系统理论对负荷的中长期预测进行了研究，然后基于D-S证据理论将两种方法融合，实现了组合预测；最后将提出的新的组合预测方法进行了仿真验证，仿真结果表明所提出的方法具有更高的预测精度，可为电网规划提供有效地指导。

1 回归分析

回归分析法基于分析电力负荷与各影响因素之间存在的关系，通过历史数据分析建立负荷的统计模型，最终实现负荷的预测。回归分析法具有模型简单，运算速度较快等特点，得到了广泛的应用。

实际运行中影响负荷的因素众多，本文选取两个比较重要的因素：人均国内生产总值X1和居民消费价格指数X2，建立了二元回归分析模型，对中长期负荷预测进行研究。

由于X1和X2为两个可控变量，可基于这两个可控变量建立二元回归分析方程为

式中：b0、b1、b2、σ2均为与 X1和 X2无关的未知参数；ε为随机误差。

通过历史数据，可以建立容量为n的模型样本集为

式中：ε1，ε2，…，εn服从正态分布且相互独立，记：

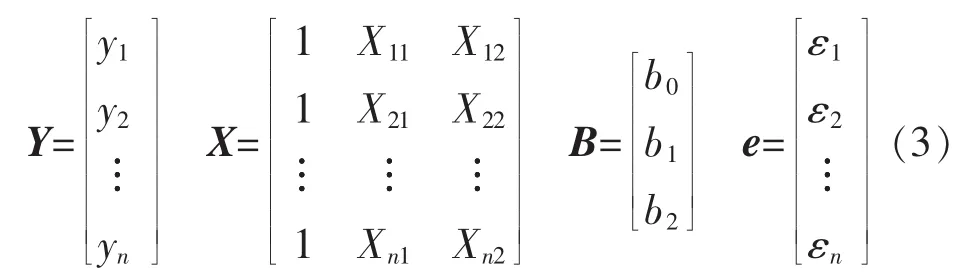
则公式（3）可变为

然后由最小二乘法求解未知参数b0、b1、b2，回归模型的参数估计为

则二元回归分析方程可表示为

2 灰色系统理论

2.1 灰色系统理论

灰色系统理论（Grey System Theory）是由华中科技大学自动化学院教授邓聚龙［14］于九十年代初首创的新学科，其主要适用于处理信息量少、数据匮乏的不确定性问题的研究。

在众多灰色系统理论模型（Grey Model，GM模型）中，GM（1，1）模型因其计算简便、实用性强等优势而在灰色系统预测领域占有较为重要的地位，灰色系统GM（1，1）模型也是灰色系统理论中到目前为止在各个领域中应用最为广泛的计算模型。

2.2 灰色系统理论GM（1，1）模型

灰色系统理论GM（1，1）模型为灰色系统理论中最为常用的一种模型，其核心基础为一个只包含单一变量的一阶灰微分方程。对灰色系统理论GM（1，1）模型进行建模。

2.2.1 对原始数列进行累加处理

首先根据原始数据建立原始数据列为

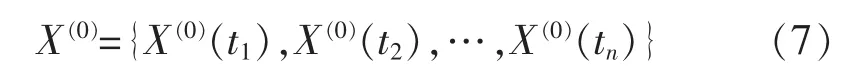
对原始数列做累加生成：

其中：

对原始数据列作了累加生成之后，就弱化了原始数据的随机性，使得生成的累加数列X（1）初步具备了指数增长规律。

2.2.2 基于累加序列构建灰微分方程

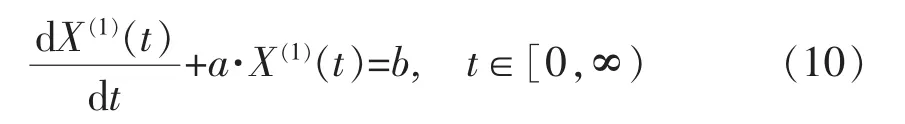
式中：a 为发展系数，反映 X（1）及 X（0）的发展趋势；b 为协调系数，反映数据间的变化关系。

2.2.3 求解参数

在求解灰微分方程（10）中的两个参数时，常用最小二乘法来进行求解：

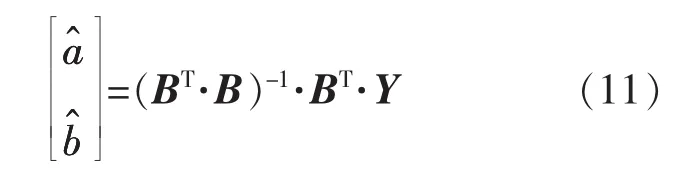
其中：

2.2.4 求解预测序列

通过以上求解过程可得：

最后经过累减生成还原，即可得到的灰色预测模型为

3 D-S证据理论

D-S证据理论由美国哈佛大学数学家Dempster于1967年提出，其发展至今已接近50年，在故障诊断、目标识别、决策支持等领域得到了广泛应用［15］。

D-S证据理论中一般将互斥的非空有限集合Θ=｛θ1，θ2，…，θn｝称为识别框架，其中 θi表示事件所有可能出现的假设，D-S证据理论中的所有概念和函数都是基于识别框架的。

3.1 基本概率分配函数

假设Θ为识别框架，则Θ上的基本概率分配（BasicProbabilityAssignment，BPA）可定义 m∶2→［0，1］满足：

式中：m（θ）表示对θ的置信度，即对θ的支持程度。

3.2 信度函数

假设Θ为识别框架，则Θ上的信度函数（Belief Function，Bel）定义为：

式中：Bel（θ）为θ的可信度，表示对命题θ的总体可信度，但还不能反应对θ的怀疑程度。

3.3 似然函数

假设Θ为识别框架，由基本概率分配函数导出的似然函数（Plausibility Function）定义为

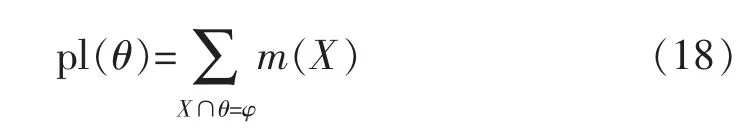
式中：pl（θ）∶2θ→［0，1］为 Θ 对应于 m 的似然函数，表示证据怀疑θ的程度。

3.4 合成规则

设Bel1和Bel2分别为识别框架Θ上的两个可信度函数，m1和m2分别对应基本可信度分配，焦元分别为 A1，A2，…，Ai和 B1，B2，…，Bj；设m2（Bj）＜1，则有证据合成公式：

其中，当A为空集时，m（A）为零。

4 基于D-S证据理论的组合预测

引入D-S证据理论将回归分析方法和灰色系统理论的优点进行了结合，建立了基于D-S证据理论的组合预测模型。

建立的模型将回归分析求得的预测值1及灰色系统理论求得的预测值2作为D-S证据理论识别框架中的两个假设，然后根据证据理论的计算步骤，结合式（19）将两个值进行融合，实现了组合预测。具体实现步骤如图1所示。

分别将回归分析及灰色系统理论得到的两个预测值1、2作为初始区间的上下阈值，然后将此区间进行等分，构建识别框架。为了验证区间等分数对最终计算结果的影响，以三等分及五等分两种等分方法进行了对比计算。计算结果表明，针对本文提出的组合方法，五等分构建的识别框架具有较高的准确性，因而本文选择对初始区间进行五等分。

假设两种方法计算得到的预测值分别为S1、S6，则进行五等分后构建的识别框架为

图1 组合预测流程

然后基于识别框架确定信度分配，为了与实际情况实现较高契合，本文选择将本领域内多个专家的意见作为信度分配的依据，专家信度分配格式为

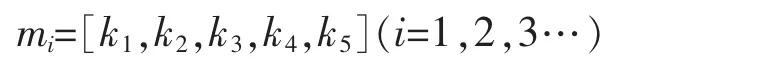
最后将得到的识别框架与信度分配基于证据合成公式（19）计算出支持度分配，确定最终预测区间及预测值（区间均值），得到组合预测结果。

5 仿真验证

选取某地区1992—2001年的用电量作为仿真计算样本，针对提出的方法进行了计算验证。表1给出了基于D-S证据理论的组合预测模型与实际值及回归分析模型、灰色系统理论模型的预测结果。

表1 负荷预测结果

由表1和图2中计算结果可知，提出的组合预测方法相对于回归分析模型及灰色理论模型均具有较高的预测精度，因而表明提出的中长期负荷预测方法可以较好地适应电网规划要求，有较高的实用价值。

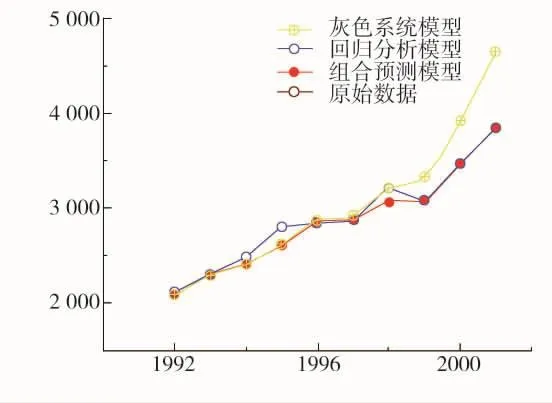
图2 仿真结果对比图

6 结语

提出了一种基于D-S证据理论的新的电力负荷中长期预测组合预测模型，能够提高负荷预测的精度。分别通过与回归分析模型、灰色理论模型验证对比，验证了本文提出组合预测模型的精度比较高，符合电网企业的要求。针对本文提出的组合预测模型，共进行了数百组数据验证，验证数据表明预测结果与实际值的误差很小，证明本方法模型具备较高的实用价值。