基于相关系数原理EMD的转子故障特征提取方法研究

吕世鹏

（新疆大学 机械工程学院，乌鲁木齐 830047）

转子系统是常见的机械传动形式和核心部件，转子的故障诊断方法一直是机械可靠性研究领域的热门及重点之一。信号时频分析方法的性能和对故障特征的提取效果直接决定故障诊断的品质。传统的分析方法如Wigner-Ville时频分布和小波变换等方法随着应用领域的扩展和研究的深入开始暴露出不足之处[1]。为此，人们提出了新的信号时频分析方法经验模态分解（EMD），它解决了传统时频分析方法的线性和自适应性分析问题。本文在试验实例中，运用EMD方法对碰磨故障的转子振动信号进行分解分析，利用相关系数原则来加强EMD方法本身的降噪滤波特性，对分解产生的本征模态函数（IMF）进行筛选降噪处理并分析其时频特征，使得特定故障特征清晰化，进而完成特征提取[2]。

1 EMD方法

EMD方法是一种自适应分解方法，为了能将信号表达为一系列代表信号内包含的各个成分的分量之和，IMF被定义出来。类似于傅里叶变换，可以将信号表达为正交的弦函数序列之和，IMF也需要满足一定的条件才具有数学和物理意义：可以满足包络计算的极值点数量和局部包络均值为零。这两个条件也是为EMD的分解步骤而设定的。

将一个信号通过EMD方法分解为IMF序列之和，需要先提取信号的极值点，以极值点为基点使用三次样条插值法构造信号包络线；用构造的上、下包络线计算出包络均值数据序列，该序列代表了信号的静态成分；期望得到的有振动成分代表意义的IMF在滤去该静态成分的信号中，即用于原信号数据序列与包络均值的求差结果中；得到的分量继续作为原始信号进行上述分解过程，其中若有分量满足IMF定义条件判断，即为IMF主分量，后续重复计算判断得到其他IMF分量[3]。若出现所得分量无法满足分解计算条件（成为单调函数）则分解结束，原始信号可以表达为：

式中，ci（t）为分解出的第i个IMF分量；r（t）为余项分量。

2 基于相关系数原理的EMD降噪及特征提取

实际上，IMF分量并不都是具有单一物理意义的，噪声的干扰会造成分解筛选过程出现模态混叠及虚假分量。为找出这些无关分量，降低或消除噪声的干扰，人们通过能反映函数序列的关联程度的数值参数作为指标准则来进行筛选识别。

相关系数的计算过程为：

式中，ρi为第i个IMF分量与原信号的相关系数，取值范围为0到1，N为采样点数量。

IMF分量根据分解顺序应按照主成分到无关成分的趋势排列，故从整体上相关系数变化应呈较小的趋势。然后，判断含有无关噪声成分的分量和虚假分量从何阶开始出现，需要以相关系数作为参考阈值。本文取一次分解所有IMF分量中的最大相关系数的十分之一为参考。

3 试验分析

试验分析验证实例为：使用美国Bently公司RK-4转子故障试验平台进行故障试验，采集振动信号对提出方法的效果进行验证。设置采样频率为1024Hz，转速4000r/min，转频66Hz。分别采集正常运行和碰磨故障情况下两组实信号，如图1所示。

图1 采样信号

从时域图谱可以看出，故障程度较严重，但无法提取故障对用的特征。对故障采样信号进行EMD方法处理，可得到7项IMF分量以及一项余项，根据式（2）分别计算8项分解结果的相关系数，如表1所示。

可以看出，筛选阈值约为0.068，保留前三阶分量即IMF1～IMF3，如图2所示。

保留的IMF分量是振动的主要成分，滤去了虚假分量和无关噪声成分。此时，用保留IMF分量重构信号，如图3所示。对重构信号进行频域分析，对比IMF主要分量和正常振动信号的频率特征，如图4所示，可以对碰磨故障的振动特征进行提取。

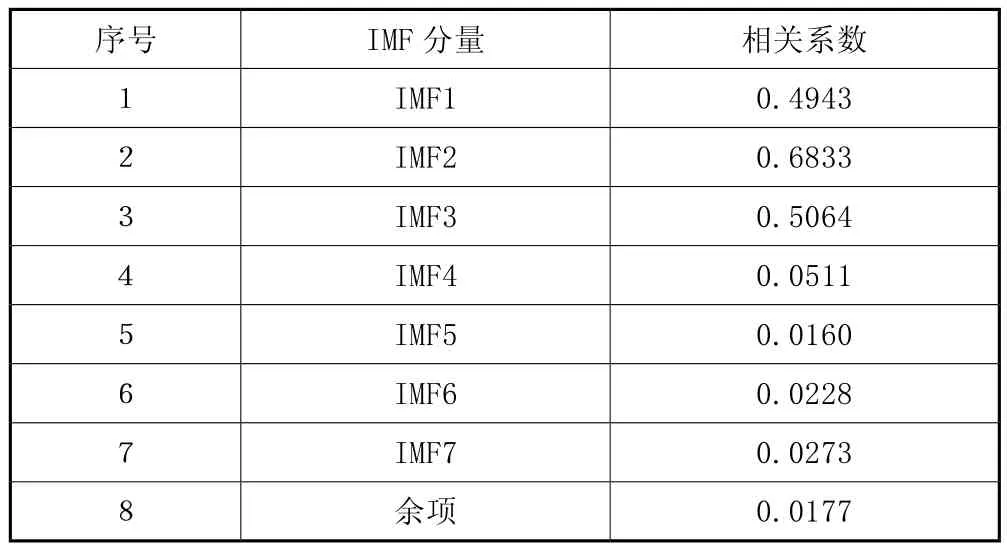
表1 8项分解结果的相关系数

图2 前三阶分量

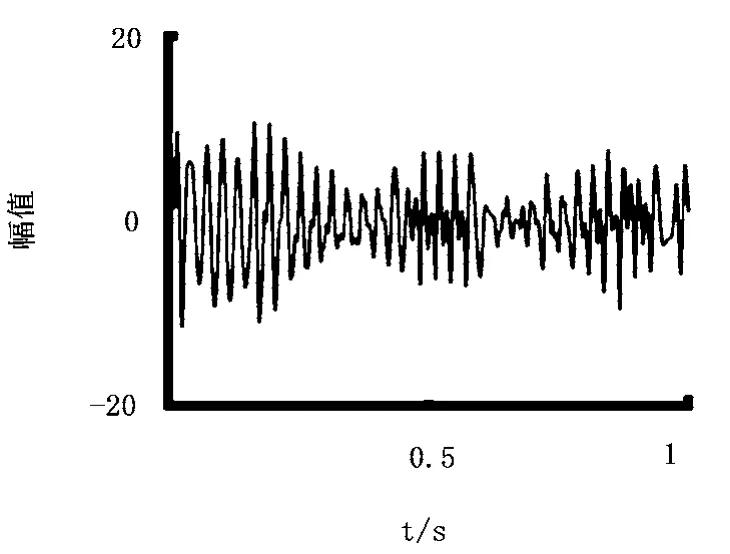
图3 重构信号

图4 频域幅值谱对比

碰磨故障对转子系统产生的振动冲击频率应该基本和转频一致或者是其倍频。实际从频谱上分析时，从图4（a）中可以看出，主频特征是2倍频和30倍频，而碰磨故障信号的频谱首先出现了以1倍转频和15倍频为中心的频带成分，其次这些频带成分是以转频为带宽。所以，主频成分的半频效应和以主频的半频频率为中心的频带带宽可作为碰磨故障的特区特征。

4 结语

通过提出一种基于相关系数原理EMD的特征提取方法，在试验验证下，笔者最终得出以下结论：分析EMD方法对信号进行自适应尺度分解的原理后，在合适的筛选条件下，该方法具有良好的滤波消噪基础；将相关系数作为阈值引入EMD方法中，可以起到很好的消噪效果，能够提取出转子碰磨故障的特征；EMD作为故障诊断领域提出时间较晚的方法，还有很大的发展活力，对比分析更多的故障特征频谱信息，故障特征提取的准确性可以进一步提升和验证。