Mining Frequent Sets Using Fuzzy Multiple-Level Association Rules

Qiang Gao, Feng-Li Zhang, and Run-Jin Wang

Abstract—At present, most of the association rules algorithms are based on the Boolean attribute and single-level association rules mining. But data of the real world has various types, the multi-level and quantitative attributes are got more and more attention. And the most important step is to mine frequent sets. In this paper, we propose an algorithm that is called fuzzy multiple-level association (FMA) rules to mine frequent sets. It is based on the improved Eclat algorithm that is different to many researchers’ proposed algorithms that used the Apriori algorithm. We analyze quantitative data’s frequent sets by using the fuzzy theory, dividing the hierarchy of concept and softening the boundary of attributes’ values and frequency. In this paper, we use the vertical-style data and the improved Eclat algorithm to describe the proposed method, we use this algorithm to analyze the data of Beijing logistics route.Experiments show that the algorithm has a good performance, it has better effectiveness and high efficiency.

1. Introduction

Now we are facing an increasingly wide range of data types from the original single Boolean attribute data sets to the current mixed type attribute data sets. There are many association rule algorithms based on the Boolean data and improved algorithms[1]-[3]. For association rules[4],denotes attributesAandBwould recommendC, andmeans that the attribute might be the quantitative data, and it may have some parameters such as the frequency. So in the,although the attribute Sunny belongs to the Boolean attribute,the attributes temperature and wind speed are quantitative attributes which have different domains such asThe values of these quantitative attributes will influence the result of data mining:

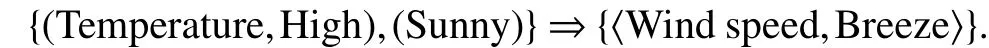
Researchers have applied the fuzzy theory, founded by Professor L. A. Zadeh, to data mining. Take the following records as an example to illustrate the fuzzy theory, {(Pathe horror movie, 8.9, 1), (Imagenes horror movie, 8.7, 4)}.Each record has three parts, the first part is the name of attribute’s ID, the second part is the evaluated point from people, and the third part is the frequency. If we suppose that the profit of Imagenes horror movie is much more than that of Pathe horror movie, the fact could not be neglected that there are different weights even if their frequencies are low. These attributes should have their own weights, which are the key of the method using association rules to find the potential relationship. In real world, we are usually interested in approximate description of attributes rather than pointing out the detailed description of some attributes to recommend other attributes.

In this paper, we propose an algorithm called fuzzy multiple-level association (FMA) rules. The rules of algorithm to solve non-Boolean attributes are as follows: 1) We use the approach based on weight and use the fuzzy theory to deal with the frequency of attribute and the value of attribute,respectively. 2) We use the concept hierarchy theory to encode concept trees and divide them into different levels. 3) This paper proposes the algorithm FMA that uses the improved Eclat algorithm as a basic model to deal with frequent sets called CH_Eclat. CH_Eclat uses non-frequent 2-itemset to cut down a large number of useless candidate sets. CH_Eclat also uses a method based on lost support values called Lost_Support to cut down times to count support. Therefore we can get frequent sets more fast according to the verification of experiment.

2. Related Works

In 1993, R. Agrawalet al.first proposed the concept of association rules[5]. R. Agrawalet al.proposed a famous algorithm Apriori[6]to count the support, and J.-W. Hanet al.[7]put forward the Fp-growth algorithm to solve the problem of generating a large number of candidate sets. These two methods are based on the horizontal format of data. References[8], [9], and [10] used the Apriori algorithm to mine multi-level rules. M. J. Zaki[11]proposed the Eclat algorithm to use the vertical data to store database’s records. This algorithm’s performance is generally better than horizontal format data.And many papers have improved the Eclat algorithm[12]-[14].Reference [15] improved the Apriori algorithm to mine real data compared with the Fp-tree algorithm, but their ways of counting support were not appropriate to deal with non-Boolean data. Reference [16] discussed some algorithms in association rules mining in recent years such as fuzzy Fp-tree.

References [8], [9], and [10] proposed several methods for the multi-level association rules mining, and the fuzzy theory is applied to the association rules in [8] and [10], which describes the attributes’ frequency by using the fuzzy set.Reference [8] proposed a fuzzy multiple-level mining algorithm for items which have different minimum supports.Reference [9] presented a partition technique for the multilevel association rule mining problem, it improves the cost of I/O and central processing unit (CPU) runtime. Reference [10] also used different support values at each level as well as different membership functions for each item, it adopts a top-down progressively deepening approach to derive large sets. But these algorithms only consider the frequency of the attributes,they do not consider that some factors may also affect the mining efficiency, such as the evaluation by people or its quantitative features.

Some other researchers also concerned about quantitative rules and multi-level mining[17]-[19]. In [20], M. Kaya proposed effective mining of fuzzy multi-cross-level weighted association rules. It invented a fuzzy data cube facilitating for handling quantitative values of dimensional attributes, and as a result, mining fuzzy association rules can be used at different levels. Since it is based on the traditional Apriori mining algorithm, it inevitably costs much CPU runtime and makes it difficult to deal with massive sparse data.

3. Basic Model of FMA Algorithm

The traditional Eclat algorithm uses the vertical format to find the frequency set. It uses the depth-first search strategy and bases on the concept lattice theory. And it divides the search space by the relationship of prefix equivalence, using crosscounting to count the support. In this paper, instead of applying the basic Eclat algorithm, we propose an improved algorithm CH_Eclat, which is more suitable for FMA.

3.1 Theorem and Basic Concepts

Theorem 1.1.A superset of the non-frequent set is certainly a non-frequent itemset.

Theorem 1.2.Non-empty subsets of any frequent itemsets are also frequent itemsets.

3.2 Improved Algorithm

1) The traditional Eclat algorithm uses the depth-first search strategy, while CH_Eclat uses the breadth-first search method to connect attribute sets. We fully use Apriori’s transcendental nature to prune the candidate sets by non-frequent 2-itemset. And non-frequent 2-itemset uses the vertical format to store the relationship of attributes.According to Theorem 1.1, non-frequent 2-itemset will greatly cut down the generation of non-frequentk-itemsets (k>2). For example, a transaction databaseZhas six attributes, by mining frequent 2-itemset simultaneously,we will obtain a non-frequent 2-itemset, such as

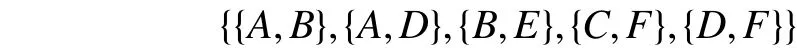
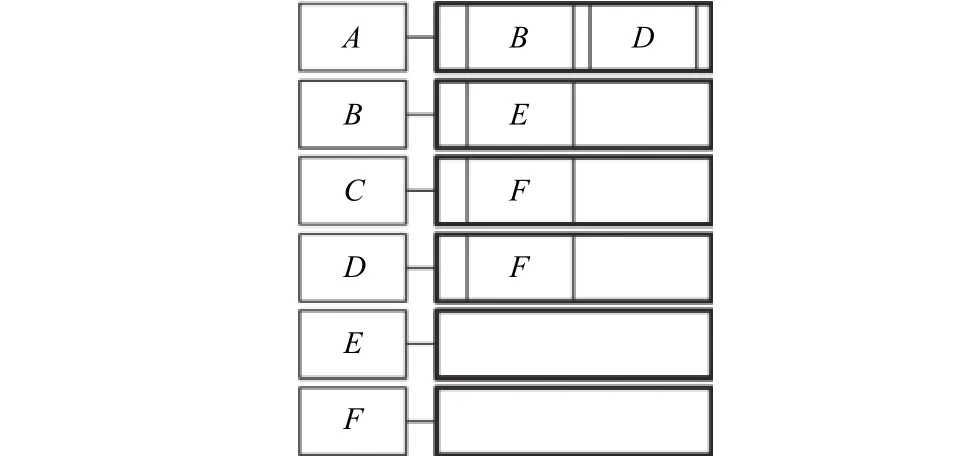
Fig. 1. Non-frequent set.

2) Combined with [21], using a missing threshold called Lost-Support based on cross-counting computing. The crosscounting method reduces the times of comparisons. For example, this attribute set {A,B}, pointerp1points toA’s first data and pointerp2points toB’s first data. Firstly, we compare the value of (*p1) with the value of (*p2), judging that if (*p1) is equal to (*p2). If they are equal, thenp1=p1+1 andp2=p2+1. If they are not equal and (*p1) > (*p2), thenp2=p2+1 and preparing the next comparison operation, where * is the pointer. In this method, the operation times are determined by

.

So we can make full use of Lost_Support to reduce unnecessary comparisons. For Table. 1, we get

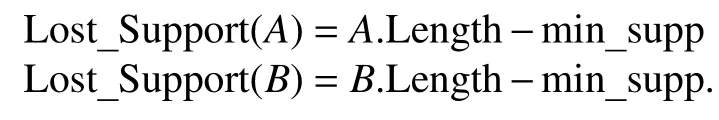
Table 1: Example of vertical-style data

When the value ofAis not matched to that ofB, the Lost_Support ofAwill be cut down by 1, so asB. If any Lost_Support is less than 0, we will break the counting and delete this relationship {A,B}, and the operation of counting is shown in Fig. 2.

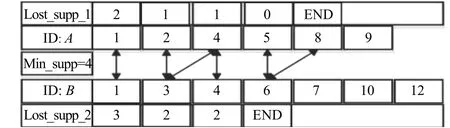
Fig. 2. Cross-counting method of Lost_Support.

3.3 Description of CH_Eclat Algorithm

The CH_Eclat algorithm is descripted as Table 2.

Table 2: CH_Eclat algorithm

4. FMA Algorithm Model

4.1 Theorem and Basic Concepts

Definition 2.1.A databaseis consisted ofnrecordsmeans it is in the vertical format. Each record TIDjof databaseZcan define as

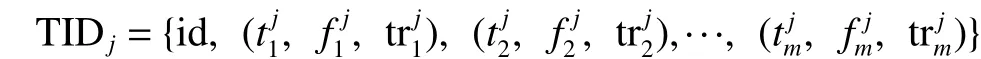
Each record has a unique tag named idthat is attribute’s frequency in record TIDj.is the value of attribute,, wheremis the number of TIDj’s attributes.

Definition 2.2.Set fuzzy record about.We getkabstract concepts from frequency, and it is corresponding to(s=1, 2, ··,k), so,and we callas a frequency membership function for attributeon TIDj.Then we getqabstract concepts from,and we know that it is corresponding to(h=1, 2, ··,q), soAnd we callas the value membership function for attributeon TIDj.

4.2 Model Description

The proposed algorithm FMA use the hierarchical coding method to get the coding tree and fuzzy set to deal with frequency of attributes and attributes’ value, with which we can get frequent sets. The concrete steps are shown as following:

Step 1. Concept hierarchy

The concept is usually expressed in the form of a hierarchical structure tree, each node is representing for a concept, the root node ANY is a special node. A given multi-dimensional attribute has many functions, including constructing many views, generating concept hierarchy,explaining the partial order and total order of attributes by patterns, and defining the construction of hierarchical tree.There are many ways to construct the tree, we can divide concept by data set’s own feature and hierarchical model.

First, we should encode the concept from the concept tree. And we can use (1) to calculate the concept’s code value,

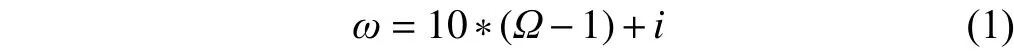
whereΩis the hierarchical level,iis the position of the current level of the layer to its ancestor node, the value of attribute coding is incremented by one from left to right,andis to encode the predefined taxonomy.Fig. 3 shows a simple case.

After using (1), the hierarchy coded tree is gotten, as shown Fig. 4.

Fig. 3. Hierarchy original tree.

Fig. 4. Hierarchy coded tree.

Step 2. Convert the frequency of attribute to fuzzy set

First, define the membership functions of attributes’frequencies, then membership functions are set according to the results of root node’s sub node classification. The corresponding frequent fuzzy set ofis obtained as

Step 3. Get representative fuzzy domain for frequency

Obtain the statistics of the number from every item fuzzyFind every item’s maximum cardinal number which hassfuzzy domain, and use the maximum cardinal number to represent the fuzzy domain of this item. Use (2) to calculate the maximum:

Step 4. Dealing with value of attribute

Define the membership function of attributes’ value,divide intogattribute areas, and calculate their membership. We will get the fuzzy set of

forming as

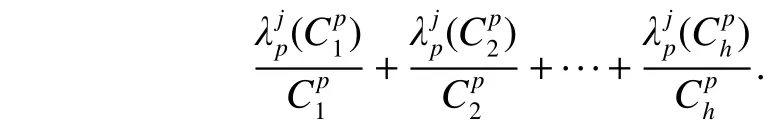
Delete the fuzzy set that is not belong to certain conditions andwill be divided into regional attributes.

Step 5. Add the weight coefficients

Calculate every fuzzy attribute’s final supportby the weight coefficients table. The judgment of weight is based on the expert opinion or other ways such as market rules for sales:

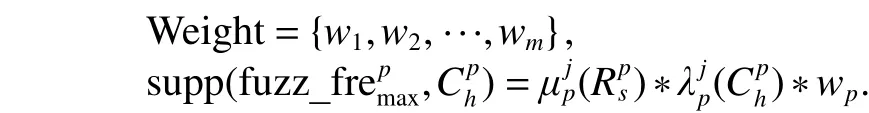
Finally, we will get the handled database which we need.

Step 6. Getting frequent itemsets by CH_Eclat.

Defining the minimum support as min_supp, calculate every fuzzy attribute’s support. And we know every value of fuzzy attribute is between [0, 1], because it ensures the downward closed property. According to [22], we do not need to calculate the ancestor nodes’ supports, because we can get them from their children. Finally, we will get the frequent item set.

5. Simple Example for FMA

In this part, we show an example of films to explain the application of FMA. In Table 3, the first of item is something which users buy, the second is the purchase quantity, and the third is the score of its evaluation. We divide films into three parts: Movies, serials, and documentaries. And each type has its specific attribute. So we make them have their own membership functions according to the frequency of every attribute. Finally, we can make data mining deeply by our algorithm. The original database is showed in Table 3.

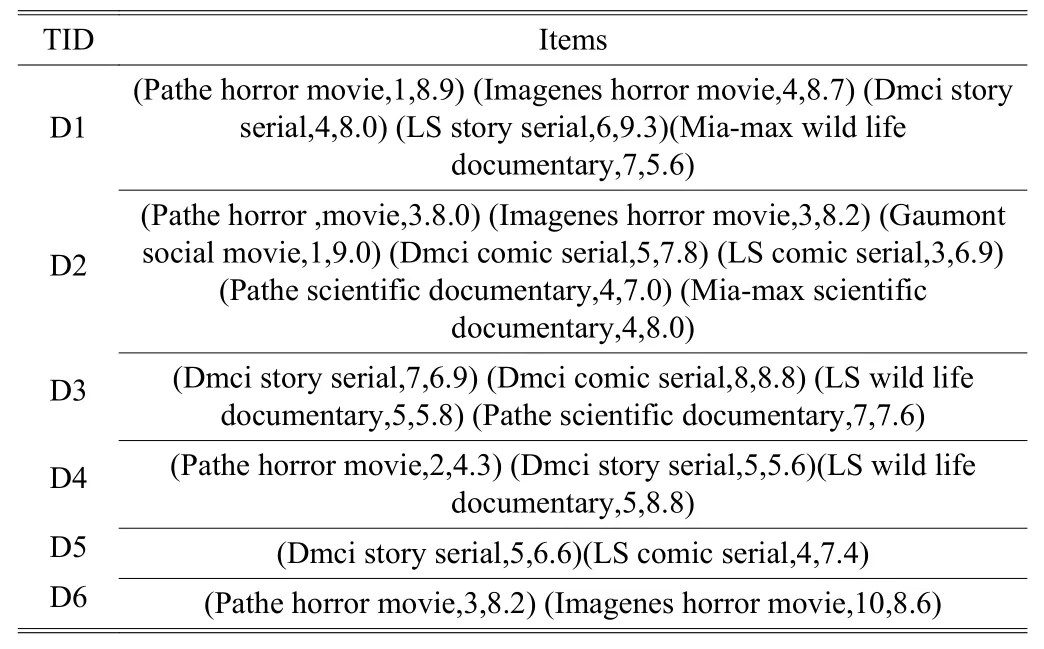
Table 3: Original database

Step 1. First, we set the relationship between a schema, and then calculate it according to (1). In this original database, the weight of each item attributes corresponds to their price and profit. And we have been normalizing the data to ensure the downward closed property. The weighting factor is showed in Table 4.

Table 4: Weighting coefficient table

We get the stratification model from the original database,and then the concept tree and coded tree will be gotten as shown in Fig. 5, and Fig. 6, respectively.

Step 2. We predefine their membership functions according to goods’ quantity and attributes classification,which are showed in Figs. 7, 8, and 9.

Then we convert the fuzzy frequent attribute according to predefining membership functions. We only show some of the data in Table 5.

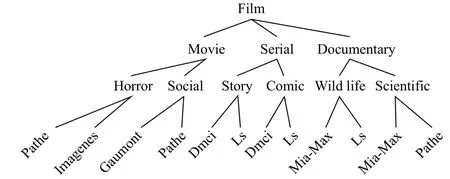
Fig. 5. Hierarchy concept tree.

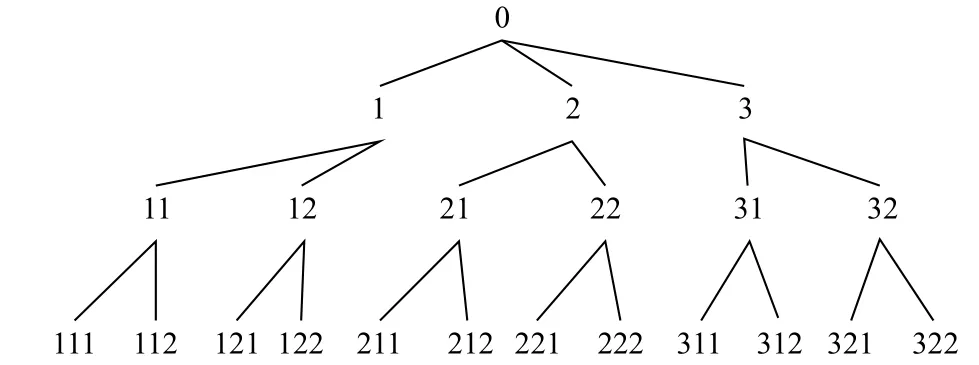
Fig. 6. Hierarchy coded tree.

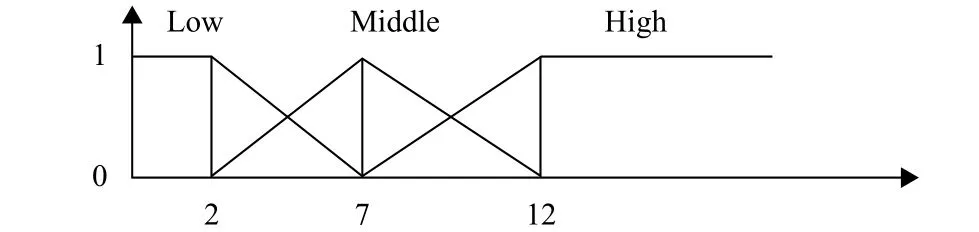
Fig. 7. Membership functions for number of serials.

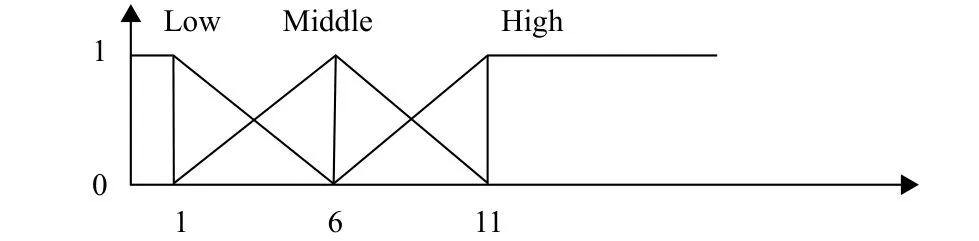
Fig. 8. Membership functions for number of movies.

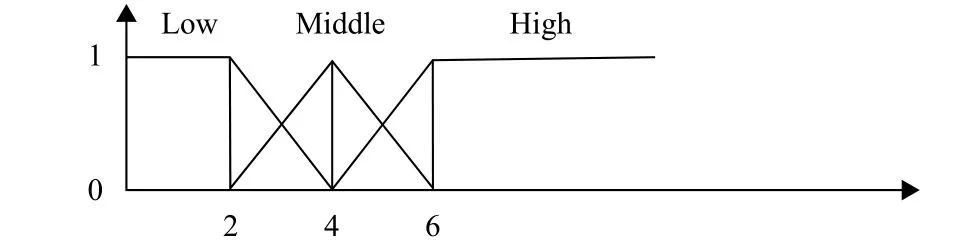
Fig. 9. Membership function for number of documentary.

Table 5: Fuzzy attribute table of frequency

Step 3. Calculate all of the transactions and find every item’s maximum cardinal number. For example, as the first transaction, we can count the number of {(111, Low)},Count111.Low=1+0.6+0.8+0.6=2.4, which is the maximum cardinal number. After counting, we will get the preprocessing the fuzzy candidate 1-itemset as Table 6.

Table 6: Fuzzy candidate 1-item set

Step 4. We construct the fuzzy concept of every attribute by score, thus we can set the fuzzy concept {Very Good,Common, Bad}. It means that the film is good, or it is common, or I do not like this film. The membership is showed in Fig. 10.

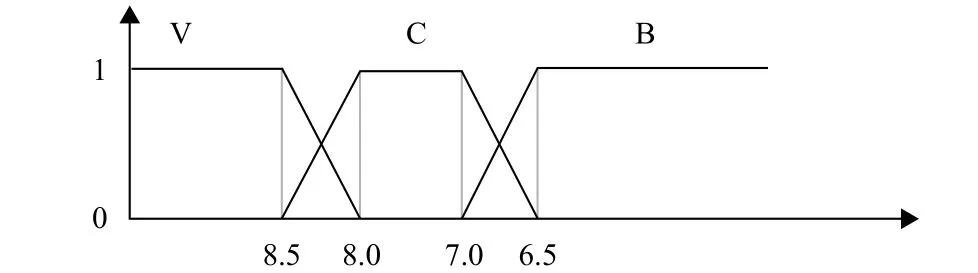
Fig. 10. Membership function.

We use (1) to convert the score to the vertical format:

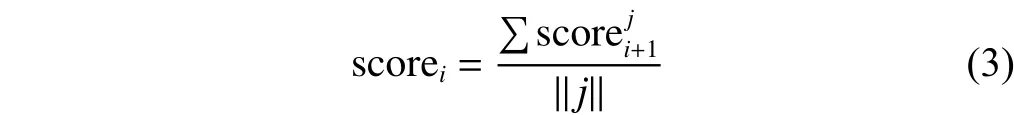
whereimeans the level of attribute,jmeans the child node number, andmeans the number of child node. It calculates the higher level attribute’s score, getting Table 7.

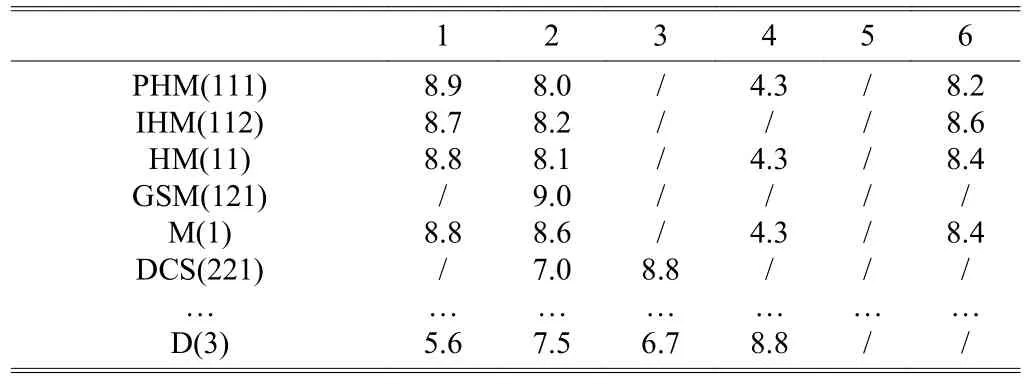
Table 7: Overall rating table

Step 5. The details of this step will be shown in the following.

1) Convert Table 7 to the membership table according to Fig. 10 and exclude the item that the sum of membership is zero. We can get Table 8.

2) Combining with the fuzzy support in Table 5, the support of quantitative value of the fuzzy attribute is found as Table 9.

3) According to Tables 9 and 4, we multiply the weight.Then we get the final support of every fuzzy attribute as Table 10.

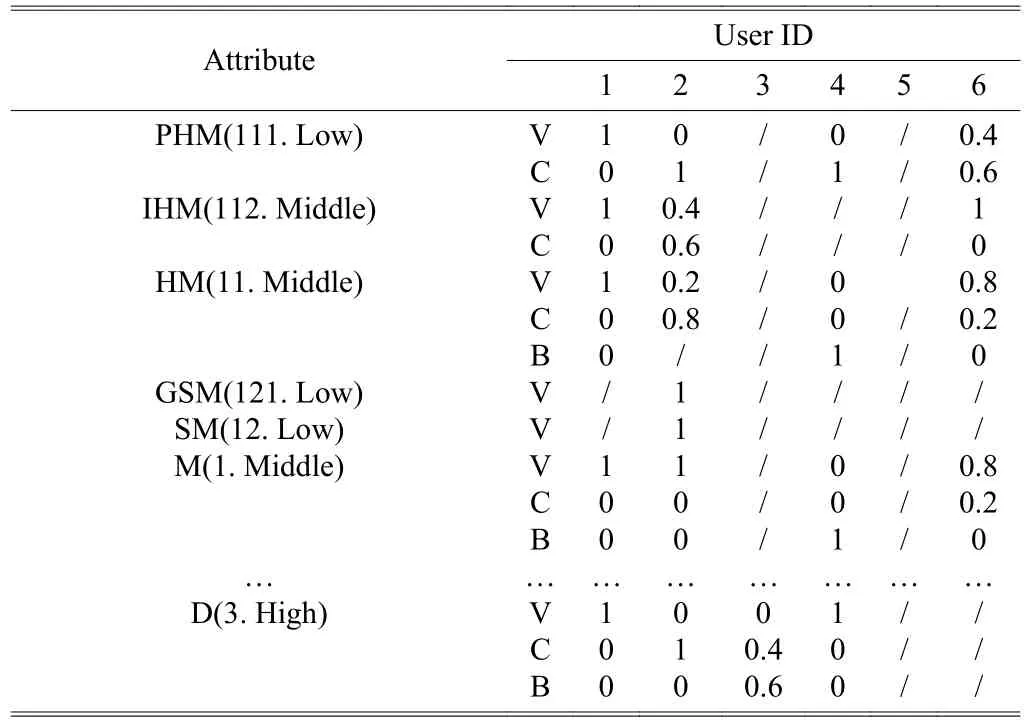
Table 8: Membership list

Table 9: Fuzzy support table

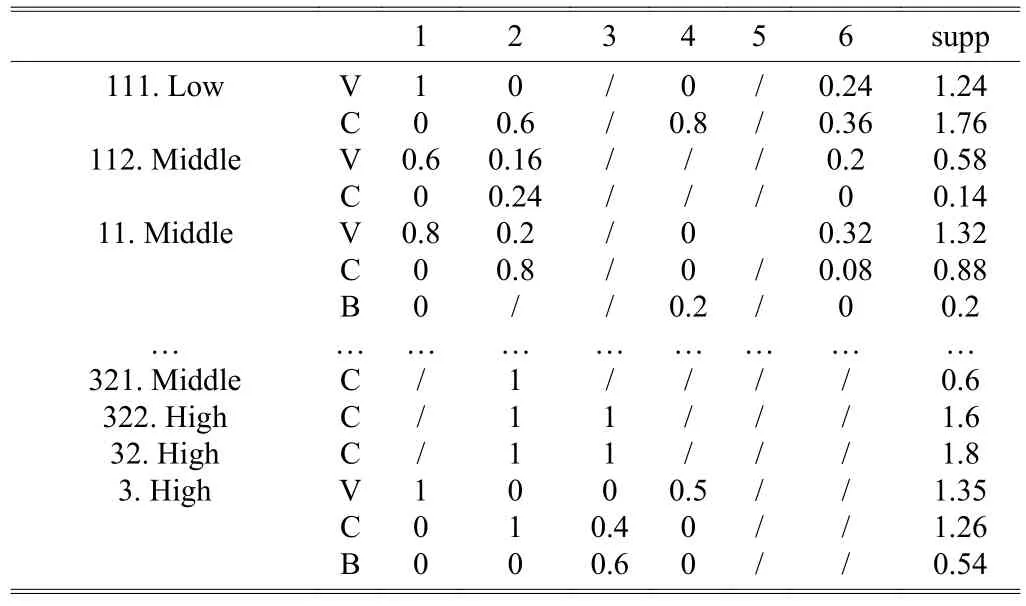
Table 10: Final fuzzy support degree table

Step 6. Set min_supp=0.8, delete {Bad} evaluation of fuzzy attribute, we will get 1-frequent item set as Table 11.

The 2-frequent itemset mining: To avoid redundancy, the child node should not connect to its ancestor node, for example,node 111 should not connect to 11, 12, and 1. The minimum fuzzy attribute set can be generated as the new set from two fuzzy attributes since every attribute set connects to another attribute set. The final mining results are shown in Table 12. In Table 12, itemconnects to. We can get from this rule: The set which includes low frequency of {Pathe horror movie} and high frequency of {Wild Life Documentary} is a frequent set,and we find their evaluation is good according to the proposed method.

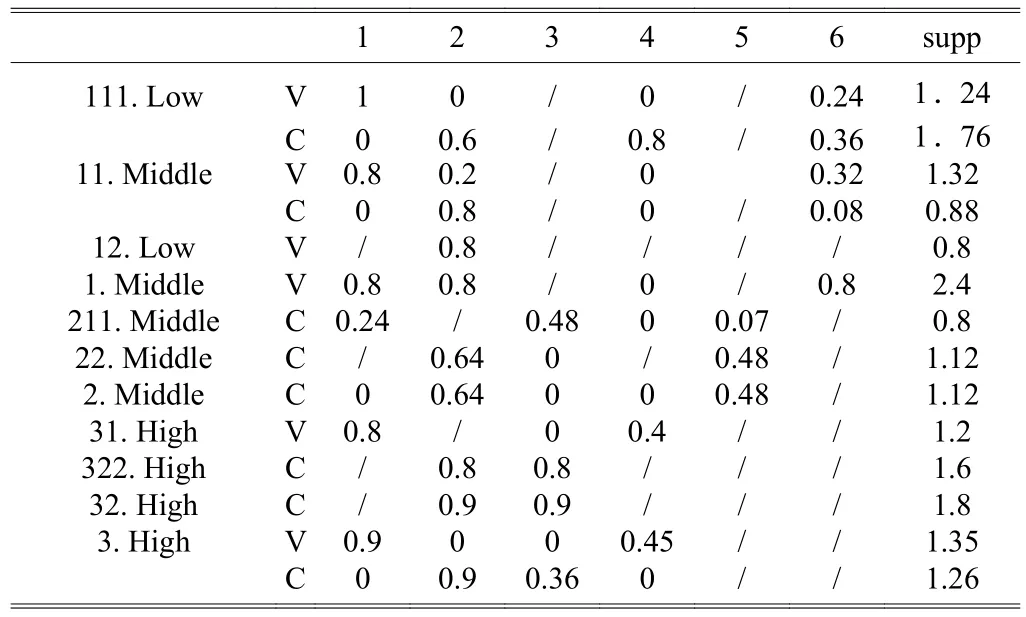
Table 11: 1-frequent item set

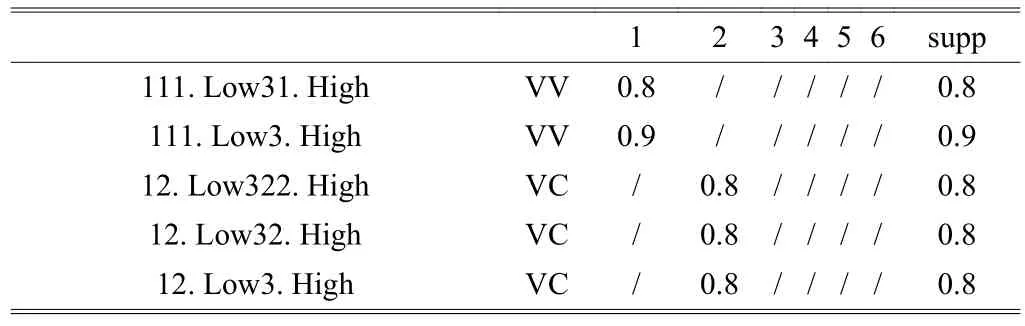
Table 12: 2-frequent set

6. Experiment Results

6.1 CH_Eclat Experiment

In this paper, we propose the FMA algorithm which is based on the CH_Eclat algorithm. We use the CH_Eclat model to count the support of database, and the performance of getting support does well affect on the effectiveness of the overall data mining. We improve the original Eclat algorithm to adapt our FMA algorithm. We use three kinds of standard data set to test our CH_Eclat algorithm and get the performance of it. The algorithm test lab environment is: CPU is AMD A8-7650K Radeon R7, 10 Compute Cores4C+6G 3.30GHz, 8G Memory,and Windows 7 OS. The CH_Eclat algorithm uses JAVA language and debugs in the Eclipse development platform. We set different support to get their run time. The console of experiment is showed in Table 13.

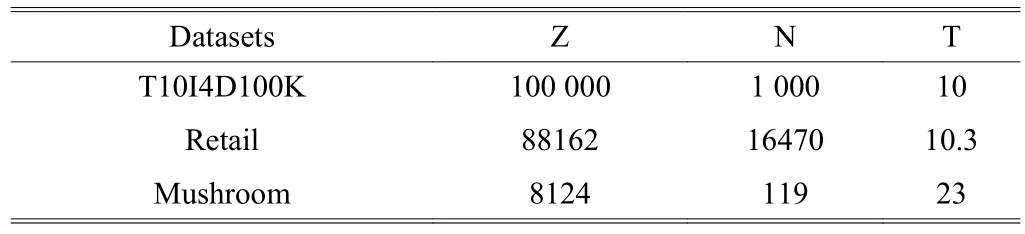
Table 13: Standard data set

In Figs. 11, 12, and 13, the CH_Eclat algorithm is compared with the standard Eclat algorithm and algorithm proposed by Z.-Y. Xiong[12]named as h_Eclat. In data set retail, the standard Eclat’s time is overflow, so we do not line it. After comparing, we find CH_Eclat has the better performance especially for the large data set and sparse data. We can quickly find the association rules with the FMA algorithm because of better support from CH_Eclat.

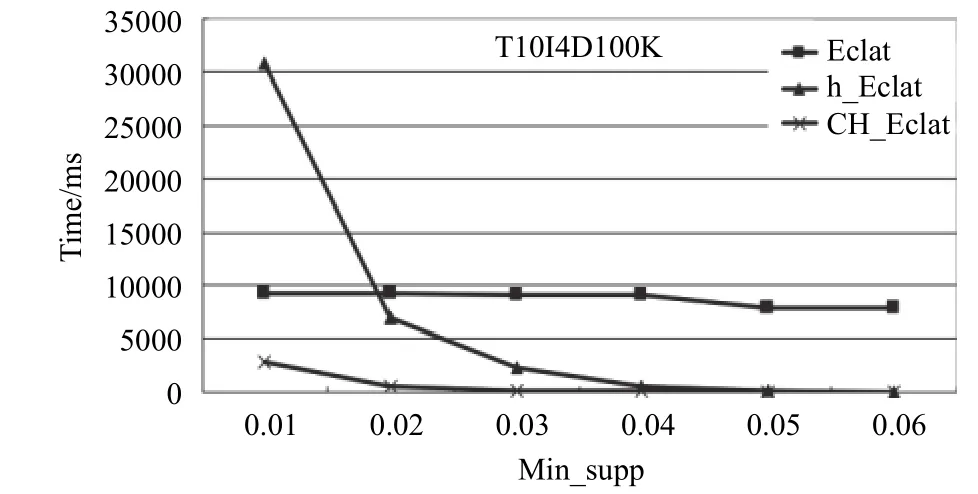
Fig. 11. Result of T10I4D100K.

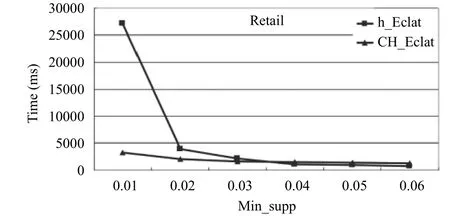
Fig. 12. Result of retail.

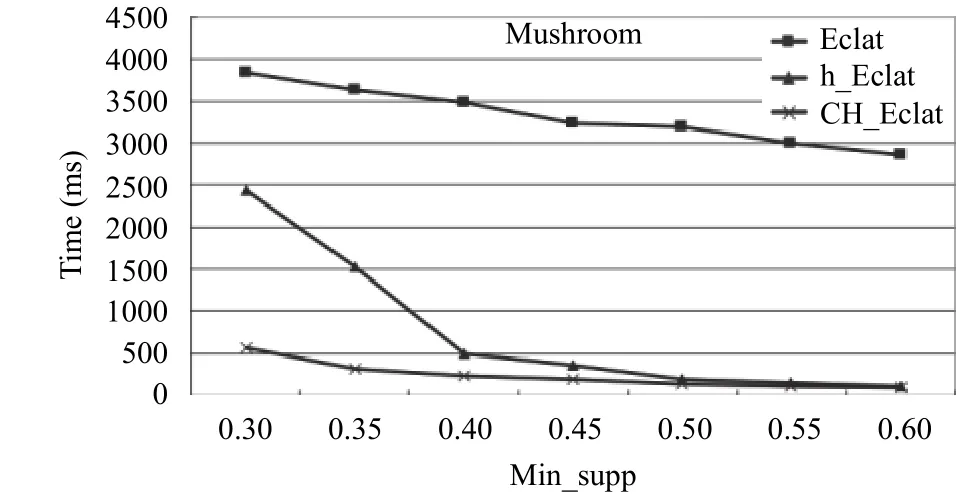
Fig. 13. Result of mushroom.

6.2 Using FMA Mining Beijing Logistics Route

We verified the validity of FMA according to the real data about the Beijing logistics route. It has 4799 logistics routes and uses different logistics modes to send their goods. We will mine the frequent route line, get potential information through peoples’ comments, and then give scores. Through the processing of the original data, the logistics send to 32 regions including several provinces,autonomous regions, and Hong Kong. It uses six types of different logistics transportation tools to send the goods to 362 municipal areas, in other words, 2453 counties in all.Due to the sparse feature of the county logistics route data,it is not conducive to analyze the frequent routes. According to the regional features and FMA, we use the province-citycounty order to construct multi-level mining. With the support of the logistics routes among different areas, we can find the frequent levels of different routes, and the result is shown in Fig. 14. We find that the route from Beijing to Sichuan is the most frequent. A lot of goods sent to Sichuan from Yanqing District, Beijing.

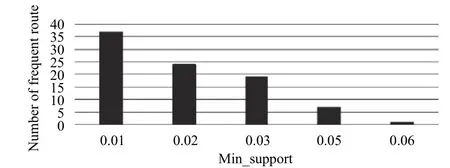
Fig. 14. Frequent routs under different support.

According to the different transportation tools used in logistics, we are able to find out the frequent levels of the use of different logistics transportation tools. The result is showed in Fig. 15. We find that a lot of goods sent to Yunan Province and Sichuan Province by Xingtie, and we also find that the goods sent to Hebei Province can get good comments by Xingtie.

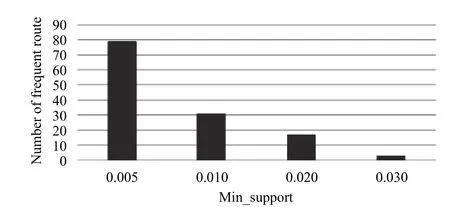
Fig. 15. Frequent logistics under different support.

After getting the frequent rules, we analyze the performance of the algorithm compared with M. Kaya’s method[20]which is based on Apriori. We set it as B_Apriori showing in Fig. 16. The result shows that the proposed algorithm has higher efficiency.

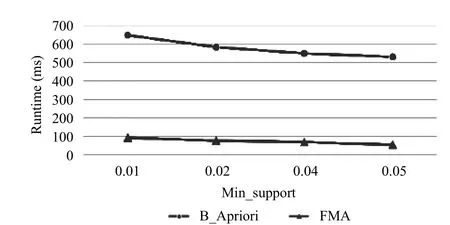
Fig. 16. Performance comparison.

7. Conclusions

In this paper, we proposed an algorithm of multi-level quantitative attributes by using the weight and combining with fuzzy theory. It is used to deal with different weights and different frequencies. With this method, we improved the data mining and got potential rules. This algorithm is much closer to the real environment. So we can do data mining by setting different conditions to obtain the target information. Our example well explained the usage of this algorithm and generated the potential rules. This algorithm is also fit for the mixed type attributes including the Boolean attribute. The good performance has been demonstrated through the data of the Beijing logistics route. It can quickly tap the frequent route. In the future, we will explore the applications of the fuzzy theory and association rules. It will promote the development of association rules.