中国辽宁典型风成黄土分维区间选取研究①
2018-07-27孙仲秀王秋兵
孙仲秀,王秋兵
中国辽宁典型风成黄土分维区间选取研究①
孙仲秀,王秋兵*
(沈阳农业大学土地与环境学院,沈阳 110161)
应用分形理论中的幂指函数关系法,选取粒径区间为无标度区,使用线性回归(linear regression)和分段线性回归(piecewise linear regression)来确定辽宁典型风成黄土837个样品粒度分维的无标度区。统计分析结果表明:一元分维的粒度分维值介于1.446 ~ 2.027,决定系数均大于0.900,确定无标度区为0.1 ~ 54.4 µm;二元分维得到节点平均值为7.64 µm ± 1.21 µm(CV=15.87%),决定系数在0.978 ~ 0.999之间变化,变异系数为0.438%,确定无标度区为0.1 ~ 7.64 µm(F2)和7.64 ~ 54.4 µm(F1), 且分维值F1>F2。二元分维值与一元分维值差异较大,从另一个侧面表明即使是同一个研究对象,选取不同标度区范围,得到的分维值及其决定系数也不同,因此,使用分维模型前要注意无标度区的选取。分维值包含着土壤发生与沉积环境信息,深入解译分维值信息有助于理解黄土-古土壤的土壤发生过程。
黄土;古土壤;分维;标度区;中国辽宁
第四纪环境演变中存在着大量非线性现象[1],这一事实得到土壤学和地学工作者们的广泛关注[2-4]。近年来,分形理论(fractal theory)被广泛应用于地貌与沉积物研究,以探讨分形特征可能指示的环境意义[1]。粒度是碎屑沉积物的重要结构特征,是判断其沉积环境的一个重要指标[5]。在研究土壤粒度时,很多学者发现土壤粒度也具有分形特证[6-7],并且分维模型可以用来很好地描述土壤粒度分布特征[8-9]。因此,土壤粒度分维值作为一种新的粒度指标被提出[8-9]。然而自然界土壤的分形不像理论[10]或破碎实验[11]那样理想化存在标度区(scaling range),土壤作为研究对象是否为分形的区别准则是无标度的[12]。其中,无标度区是指分形关系成立的尺度范围,是统计分形中的一个重要界定,但这个定义没有界定一个统一明确的无标度区范围[13]。目前,多数学者采用土壤粒径来表示无标度区,再依据无标度区定义和自身经验来确定无标度区的具体范围,由此导致无标度区范围各不相同,如0.275 ~ 630.957 µm[4],2 ~ 节点(cutoff)~ 1 000 µm[14],0.5 ~ 节点 ~ 5 000 µm[1,8], 0.02 ~节点(0.05 ~ 0.1 µm) ~ 节点(10 ~ 5 000 µm)~ 5 000 µm[9], 0 ~节点(0.51 µm)~节点(85.3 µm)~ 2 000 µm[15]等。在这种情况下针对同一研究材料,不同研究者选取的无标度区的范围也有可能不同,这不利于大量样品分维值的计算与比较。无标度区的选取对粒度分维值至关重要[4],为此,必须注意无标度区的选取。尤其,在一定研究区域内,选取合适的无标度区才能更好地对该区典型土壤进行粒度分形研究,获得沉积物粒度分形的一些新认识,服务于沉积环境演变和土壤发生学研究。
1 材料与方法
1.1 研究区概况和土壤样品采集
朝阳剖面(Chaoyang section,41°33′9.6″N,120°30′20.8″E;图1)位于辽宁省西部低山丘陵区松岭山脉中段的朝阳市凤凰山,地处中国黄土分布区的东北角。该区年平均气温和年平均降雨量分别为9 ℃和450 ~ 500 mm。朝阳剖面深19.85 m,包括顶层全新世土壤(S0)和向下5层黄土与4层古土壤相间分布(图2)。地层和剖面的形态描述详见参考文献[16]。Sun等[16]和陈辉等[17]的研究结果表明朝阳剖面为423 ka BP以来连续沉积而成的风成黄土-古土壤序列剖面。该剖面228 cm以上部分受到流水作用被改造为次生黄土(local reworked loess);228 cm以下部分(LOP)黄土具有母质连续性[16],是本文研究的重点。在2006年,采用2 cm高精度连续采样,在LOP部分采集了837个土壤样品,风干后,研磨过筛备用。
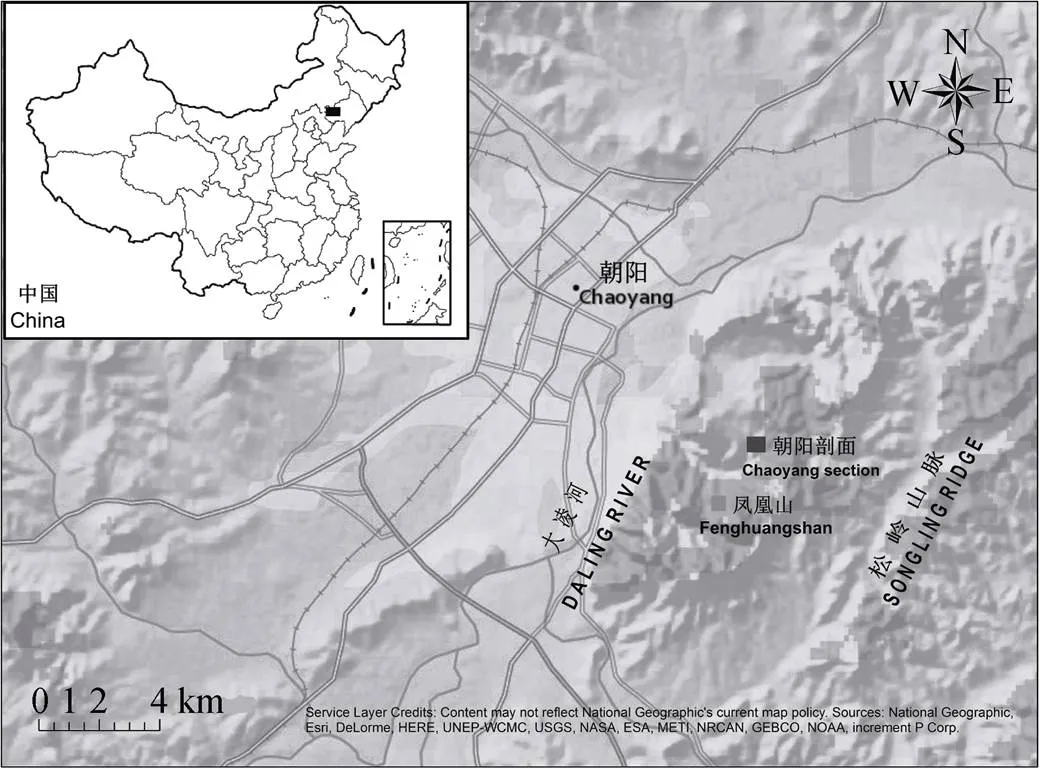
(内嵌地图上的黑色矩形指示中国朝阳的所在位置)
1.2 土壤粒度测量
土壤样品的粒度测量采用标准的样品前处理和粒度测定方法[18],使用荷兰安米德公司生产的粒度分析仪CIS-100来完成。测试粒度范围为0.1 ~ 3 600 µm,测量误差为±2.5%。
1.3 土壤粒度分维模型(fractal models)
目前线性分形应用广泛,其实质就是局部是整体成比例缩小,缩小部分具有自相似性(self similarity)[10]。分维是定量描述具有线性分形系统自相似性的参数[10],而粒度分布实质上是描述土壤开放自组织系统物质组成的分形结构[19],为此分维值作为一种粒度参数与土体演化环境密切相关[4]。
幂指数关系法是应用较广泛的测算分形维数的方法。具体计算方法为:在粒度分形集中,若其中一个粒度子集关于标度具有自相似性且该标度下的颗粒数为,则可以用如下方程描述这一关系[7, 10, 20]:
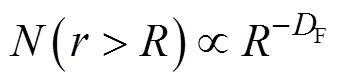
式中:(>) 是粒径大于的颗粒个数;F是分维值。
(UPP代表朝阳剖面上部0 ~ 195 cm部分;LOP代表朝阳剖面下部228 ~ 1 985 cm部分;MIP是UPP与LOP的过渡层195 ~ 228 cm部分)
图2 朝阳剖面照片及其地层示意图
Fig. 2 Schematic logs of stratigraphy with corresponding time constraints of Chaoyang section
在实际应用中,由于实验测定土壤样品粒度通常获得的是质量数据,因此使用粒径与质量之间的指数关系方程(mass-size based)较为方便和准确[7-8]。方程为:
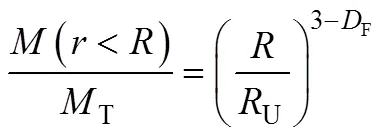
式中:(<)是指粒径小于土壤颗粒的质量和;T是指粒径小于U的土壤颗粒的质量总和;U是指所研究具有分形特征粒径集合的无标度区的上限值;F是指分维值。
对方程(2)进行自然对数关系转换得到方程(3)和(4):
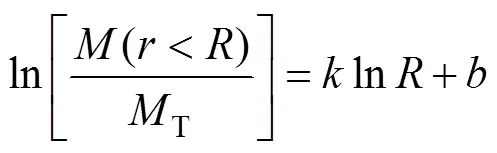
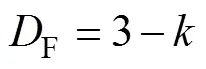
方程(3)和(4)中:为通过对方程(3)的数据点回归分析得到最高决定系数时直线的斜率;为此时方程的截距,为常数。最后分维值通过方程(4)计算获得。
基于以上计算过程推导可得到二元分维模型,经过自然对数转化后的方程为:

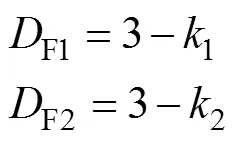
式中:lnC是粒度曲线在双对数坐标中的中间节点,将整个粒度区间分成两个部分,此时分段线性回归(piecewise regression)的决定系数最高;1、2、1和2参照方程(3)中的和释义。
2 结果与讨论
2.1 一元分维模型无标度区确定
土壤粒度分级越细,函数拟合越好,决定系数越大,分形效果则越好[4]。本文对样品小于某一粒径占总质量的百分含量((<)/T)和/U标准化后,在双对数坐标中用线性回归分析方法进行线性拟合(图3),得到直线最优参数斜率和决定系数。如图3A所示,平均粒度曲线明显存在分段线性关系,ln 54.4节点将粒度曲线分成2个单独的线性区域。粒径超过54.4 µm部分,双对数坐标中数据点基本处于一条近平行于轴的直线上。通过方程(3)和(4)计算粒度分维值F≈3,决定系数为0.16。决定系数很小,表明该区黄土在粒径大于54.4 µm范围内,粒度分布不具有分形特征。朝阳剖面LOP部分,为典型风积黄土,颗粒粒径主要集中在0.1 ~ 54.4 µm范围内。图3B,0.1 ~ 54.4 µm范围内粒径数据点,经线性回归分析得到最优参数,决定系数为0.96,分维值为1.74。
F值处于分维值的理论值区间0 ~ 3内[7],且具有非常高的决定系数值。这表明朝阳剖面LOP部分平均粒度在0.1 ~ 54.4 µm范围内具有分形特征。基于此,根据分形维数原理,对LOP的837个样品做标准化质量累积百分含量与标准化粒径的双对数坐标图,统计分析得出,粒度分维值介于1.446 ~ 2.027,决定系数均大于0.900。以上证据表明朝阳剖面黄土粒度分布的无标度区为0.1 ~ 54.4 µm。朝阳剖面风成黄土粉粒具分形特征上限节点54.4 µm与Palouse黄土(54.21 µm)和Walla黄土(50.86 µm)[15]接近。
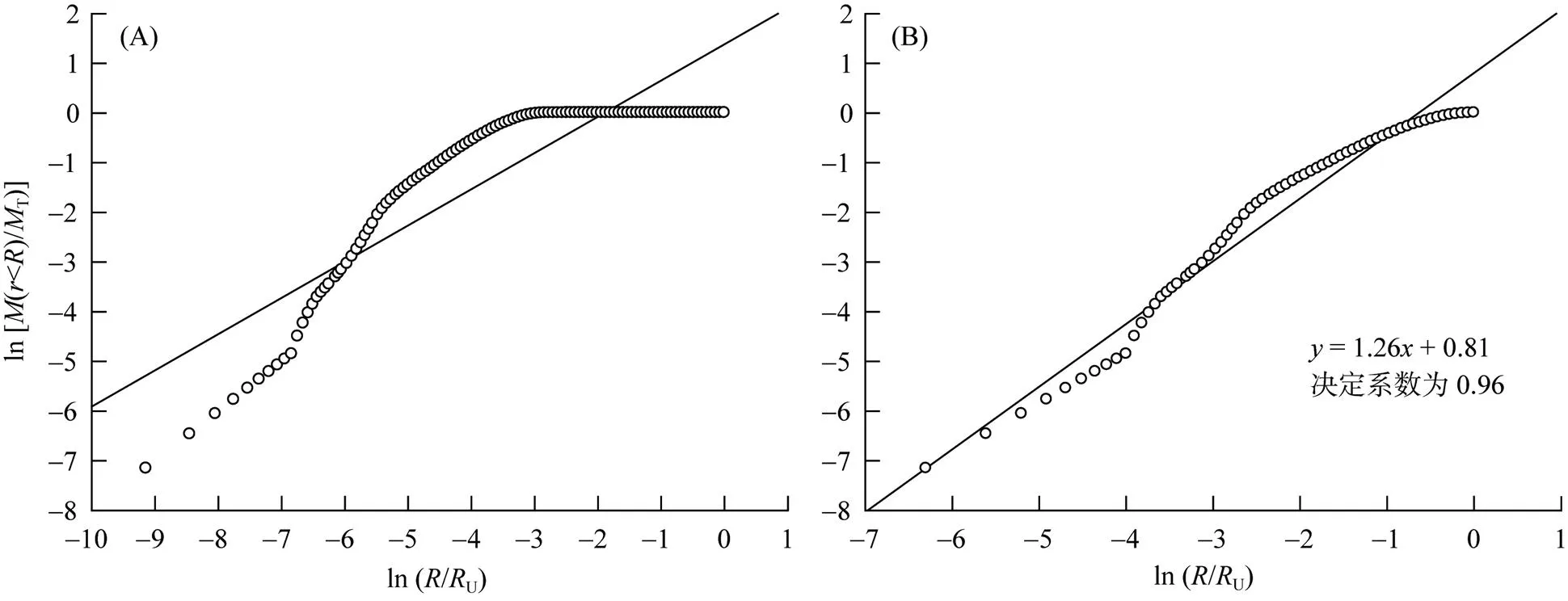
(图中符号o代表试验数据点,直线代表线性拟合最优直线)
2.2 二元分维模型无标度区确定
在二元分维模型下,利用分段线性回归分析,分析结果将0.1 ~ 54.4 µm粒度区间分成两部分,分别命名为F1和F2。根据二元分形维数原理,对LOP的837个样品绘制标准化质量累积百分含量与标准化粒径的双对数坐标图,统计分析得出,F1和F2的节点在5.04 ~ 12.66 µm,平均值为7.64 µm ±1.21 µm (CV=15.87%);决定系数在0.978 ~ 0.999变化,变异系数为0.438%;所有分维值均介于0 ~ 3[7]范围内。同时,朝阳剖面LOP黄土粒度二元分维节点值落在相似研究结果范围内:0.51[15]~ 10 µm[9]。以上证据表明朝阳剖面LOP部分具有分段分维特性,二元分维节点将一元分维无标度区进一步分成两个子无标度区,分别为0.1 ~ 7.64 µm(F2)和7.64 ~ 54.4 µm(F1),且F1>F2。F1区间主要是粗粉粒(CSI)破碎成细粉粒(FSI)的过程,F2区间主要是细粉粒(FSI)破碎成黏粒(CL)的过程[16]。二元分维得到的两个不同的分维值包含朝阳剖面风成黄土沉积后的两个不同的发生发育过程信息。二元分维值与一元分维值差异较大,从另一个侧面表明,即使是同一个研究对象,选取不同无标度区范围,得到的分维值及其决定系数也不同,因此要注意无标度区的选取。
3 结论
地处中国黄土分布区东北角的朝阳剖面,地表以下228 ~ 1 985 cm黄土-古土壤序列中粒度具有分维特征的无标度区为0.1 ~ 54.4 µm,二元分维可将其进一步划分为0.1 ~ 7.64 µm和7.64 ~ 54.4 µm两个子集。一元分维值和二元分维值包含有土壤发生和沉积环境演变信息。
致谢:在论文撰写过程中受到了Phillip R. Owens等专家的指导,在此一并感谢。
[1] Turcotte D L. Fractals and chaos in geology and geophysics [M]. Cambridge: Cambridge University Press, 1992: 1–385
[2] Steacy S J, Sammis C G. An automaton for fractal patterns of fragmentation [J]. Nature, 1991, 353: 250–252
[3] Tyler S W, Wheatcraft S W. Application of fractal mathematics to soil water retention estimation [J]. Soil Science Society of America Journal, 1989, 53(4): 987–996
[4] 张威, 郭善莉, 李永化, 等. 辽东半岛黄土粒度分维特征及其环境意义[J].地理科学进展, 2010, 29(1): 79–86
[5] 陈冬梅, 穆桂金. 不同沉积环境下沉积物的粒度分形特征的对比研究[J]. 干旱区地理, 2004, 27(1): 47–51
[6] Millán H, González-Posada M, Aguilar M, et al. On the fractal scaling of soil data. Particle-size distributions [J]. Geoderma, 2003, 117(1-2): 117–128
[7] Turcotte D L. Fractals and fragmentation[J]. Journal of Geophysical Research, 1986, 91(B2): 1921
[8] Tyler S W, Wheatcraft S W. Fractal scaling of soil particle- size distributions: analysis and limitations[J]. Soil Science Society of America Journal, 1992, 56(2): 362–369
[9] Wu Q, Borkovec M, Sticher H. On particle-size distributions in soils[J]. Soil Science Society of America Journal, 1993, 57(4): 883–890
[10] Mandelbrot B B. The fractal geometry of nature[M]. New York: W. H. Freeman and Co., 1982: 1–173
[11] Taşdemir A. Fractal evaluation of particle size distributions of chromites in different comminution environments[J]. Minerals Engineering, 2009, 22(2): 156–167
[12] 艾南山, 李后强. 第四纪研究的非线性科学方法[J]. 第四纪研究, 1993(2): 109–117
[13] 陈隅, 陈凌. 分形几何学[M]. 北京: 地震出版社, 1998: 87–89
[14] Kozak E, Sokołowska Z, Stępniewski W, et al. A modified number-based method for estimating fragmentation fractal dimensions of soils[J].Soil Science Society of America Journal, 1996, 60(5): 1291–1297
[15] Bittelli M, Campbell G S, Flury M. Characterization of particle-size distribution in soils with a fragmentation model[J]. Soil Science Society of America Journal, 1999, 63(4): 782–788
[16] Sun Z X, Owens P R, Han C L, et al. A quantitative reconstruction of a loess-paleosol sequence focused on paleosol genesis: An example from a section at Chaoyang, China[J]. Geoderma, 2016, 266: 25–39
[17] 陈辉, 王秋兵, 韩春兰, 等. 朝阳凤凰山古土壤序列粒度特征与成因分析[J]. 地球与环境, 2009, 37(3): 243–248
[18] 鹿化煜, 安芷生. 前处理方法对黄土沉积物粒度测量影响研究[J]. 科学通报, 1997, 42(23): 2535–2538
[19] Perfect E. Fractal models for the fragmentation of rocks and soils: A review[J]. Engineering Geology, 1997, 48(3): 185–198
[20] Matsushita M. Fractal viewpoint of fracture and accretion[J]. Journal of the Physical Society of Japan, 1985, 54(3): 857–860
Selecting Fragmentation Fractal Scaling Range for Typical Eolian Loess-paleosol in Liaoning, China
SUN Zhongxiu, WANG Qiubing*
(College of Land and Environment, Shenyang Agricultural University, Shenyang 110161, China)
Based on the theory of fragmentation fractal dimension, particle size data of 837 loess samples from LOP (the lower part of Chaoyang section) in Liaoning were analyzed using linear regression and piecewise linear regression to select appropriate scaling range for loess in this area. For the single fragmentation fractal dimension, values of fractal dimensions (F) are between 1.446 and 2.027 with determination coefficient more than 0.900. The scaling range of 0.1-54.4 µm was determined. While two scaling range of 0.1-7.64 µm (F2) and 7.64-54.4 µm (F1) were obtained by a cutoff of 7.64 µm ± 1.21 µm (CV=15.870%) using piecewise linear regression. The high coefficient of determination ranges from 0.978 to 0.999 with coefficient of variation for 0.438%. Furthermore, theF1is greater thanF2. TheFvalues from piecewise fractal are different from the single fractal dimension. This suggests thatFvalues could be different due to different scaling range selected for specific loess. Therefore, appropriate scaling range should be selected first before using fractal models. Due to the possible relationship with loess pedogenesis and deposition environment, interpretingFvalues is helpful for understanding loess pedogenesis and deposition environment.
Loess; Paleosol; Fractal dimension; Scaling range; Liaoning of China
国家自然科学基金项目(41771245;40971124;41371223)、辽宁省博士启动基金项目(20170520407)和国家留学基金委项目(201408210121;201508210357)资助。
(qiubingwangsy@163.com)
孙仲秀(1987—),男,辽宁营口人,博士,讲师,主要从事土壤地理学研究。E-mail:sun19871001@126.com
10.13758/j.cnki.tr.2018.03.021
S151
A
