考虑后悔厌恶的私募股权基金投资组合优化模型

胡支军,贺 阳

(1.贵州大学数学与统计学院,贵州贵阳550025;2.贵州省公共大数据重点实验室,贵州贵阳550025)

1 引 言

私募股权(private equity,PE)投资,是指以非公开的方式向少数机构投资者或个人募集资金,对未上市企业进行权益性投资,通过被投资企业上市或转让退出,获得高额资本回报的一种投资方式.PE基金投资与对公开证券市场投资的主要区别在于,它以放弃资本的流动性来换取追求长期投资的更高收益为特点.在过去的十几年间,私募股权投资在全球范围内获得了高速的发展.据普华永道2017年3月发布的一项报告显示,2016年,在人民币募资金额大幅增加的推动下,中国私募股权及风险投资基金募资创历史新高,达725.1亿美元.同时,2006年至2016年期间,中国大陆及香港市场总共募集资金超过5 320亿美元,在亚洲私募股权/风险投资基金中依旧保持主导地位.

发展PE投资,对一个国家或地区的经济增长、技术创新与劳动就业都具有明显的正面促进效应.然而,尽管PE基金作为一种资产类别已经起到越来越重要的作用,但是目前学术界关于如何将PE基金纳入整体投资组合的研究工作还相当有限.

PE基金的三个特点使得相应的投资组合优化模型变得复杂[1].首先,PE基金是非流动性投资,通常不能在其整个生命周期内(通常为10到14年)出售[2].这种非流动性是由于缺乏一个成熟的二级市场,以及对出售PE基金的合同限制.其次,PE基金的股权不能像普通股票和债券那样可以立即购买.投资者首先做出一个初始资本承诺,并在随后的时间里,作为对资本募集的回应,转移特定数量的资金给普通合伙人.第三,PE基金的现金分红不能再投资于基金,而这些支出是重要的,因为基金的生命周期是有限的.这三个特点导致投资者不能直接控制他们对PE基金的投资组合权重,而只能选择对PE基金的新承诺的规模,这将在某些滞后时间间接的影响未来的投资组合权重[1].这与现有的许多投资组合优化模型中研究的情况大不相同,在这些模型中,投资者可以动态地再调整其投资组合中所有资产的权重.

近年来,具有非流动性资产的投资组合问题引起了学术界的重视.Cumming等[3]给出了一个新的PE基准指数,讨论了新的指数如何改进包含PE基金的投资组合业绩,但该模型没有考虑PE基金投资的非流动性特征.Longstaff[4]在一个具有异质代理人的多资产交换经济中研究了市场非流动性对资产定价模型的影响.Ang等[5]给出了具有流动性资产和非流动性资产的投资组合选择模型,发现非流动性风险将导致递增的和状态依赖的风险厌恶并且减少对流动和非流动风险资产的配置.Sorensen等[6]通过求解具有风险厌恶的有限合伙人投资于由一个普通合伙人管理的PE基金的资产组合选择问题,给出了对PE基金投资的动态评价模型.Liu等[7]利用实物期权模型研究了非流动性和报酬结构对PE投资决策的影响,发现高度非流动性可能加速或延迟投资决策,管理费或提成费将导致对PE的低投资.但是,这些文献都是在经典的CRRA或HARA效用框架下研究投资者的最优投资决策问题.

在现实投资环境,投资者在投资前会对不同市场状态下各风险资产的价值进行预估,他们的判断与决策过程通常会受到认知、情绪等各种心理因素的影响,会表现出“有限理性”行为.后悔理论认为[8−10],决策者在决策过程中会将自己考虑选择方案的结果与其他方案可能获得的结果进行比较,如果发现选择其他方案可以获得更好的结果,那么决策者会感到后悔,反之则会感到欣喜.文献[11]指出,后悔理论在应用上比展望理论更具有优势.因此,在包含PE基金的投资决策中,如何考虑投资者的后悔厌恶行为偏好,选择令投资者感到最为满意的一个或多个PE基金,是一个值得关注的问题,具有重要的理论价值和现实意义.

已有不少学者应用后悔理论研究只包括流动性资产的投资组合问题.例如,Michenaudc等[12]应用后悔理论导出了最优货币对冲决策的封闭解;Mulaudzi等[13]研究了具有后悔厌恶偏好的银行对贷款和国库卷的最优配置问题;Egozcue等[14]分析了一个后悔厌恶型投资者对两个流动性风险资产的最优投资选择问题,并对后悔厌恶投资者与风险厌恶投资者的投资行为进行了比较.目前,还尚未有文献在后悔理论框架下研究具有非流动性PE基金资产类的连续时间投资组合优化问题.

随着金融市场的迅速变化,投资者通常需要根据市场环境的变化不断调整投资策略,因此,连续时间投资组合问题成为学术界广为关注的研究领域.本文的主要贡献是:1)在经典的Merton投资组合模型[15]框架内,引入非流动的PE基金,并考虑具有后悔厌恶行为的投资组合问题,给出了投资者的动态资本承诺策略,以及如何在流动性股票和债券之间最优地进行再调整;2)比较分析了不同偏好假设下的最优投资组合策略.以往的文献几乎都只考虑单一的CRRA或HARA效用函数[16],本文则同时选取CRRA和后悔厌恶两种效用函数,研究不同行为偏好对投资组合配置的影响.研究发现:后悔厌恶型投资者对PE基金的资本承诺比率低于CRRA型投资者的承诺比率,会以更谨慎的态度对待PE基金.此外,当股票与PE基金收益的相关性水平由正变为负时,后悔厌恶型投资者和CRRA型投资者对PE基金的承诺比率均由低到高逐渐增加.

2 经济环境与市场模型

2.1 经济环境

假设一个具有无限期投资机会的机构投资者(有限合伙人),可以投资三种类型的资产:无风险债券B,公开上市的股票S,非流动的PE基金F.无风险债券和股票代表经典Merton模型[15]中的标准投资机会.

无风险债券(或货币市场基金)的价格过程Bt满足

其中r表示连续复利无风险利率.为了简便,r假设为一常数.

流动性股票的动态价格St服从如下几何布朗运动

其中µS(µS＞r＞0)表示股票的预期收益率,σS表示股票收益的波动率,WS,t是标准布朗运动.这里为了简化起见,假定股票不支付红利[17].注意到,如果股票支付红利,下面的分析也是同样成立的.

进一步,借鉴文献[18]对非流动性风险资产价格过程的建模方法,假定PE基金的收益与股票的收益之间具有线性相关性,本文采用如下的几何布朗运动来描述PE基金的价值的动态演化过程

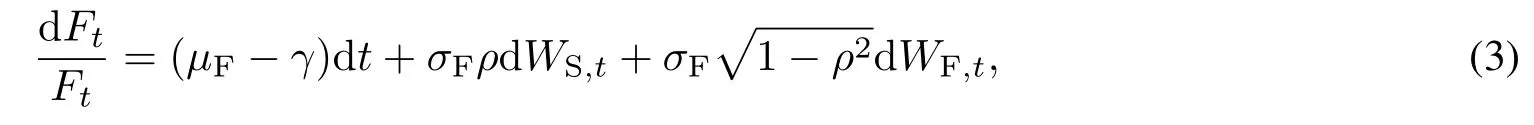
其中µF(µF＞0)表示PE基金的连续复利预期收益率,γ＞0表示PE基金支付的连续资本分配率,σF表示PE基金收益率的标准差,WF,t是与WS,t独立的标准布朗运动,ρ表示PE基金收益与股票收益之间的线性相关系数(|ρ|≤ 1).

需要指出的是,本文假定PE基金的资本分配率γ为常数,实际上,也可以考虑γ随时间确定性地或随机变化的情形.特别地,若取γ=0,则式(3)即为文献[5,6]中给出的非流动性PE基金的价格过程.

2.2 承诺资本的动态过程

由于缺乏成熟的二级市场,以及对出售PE基金的合同限制,PE基金在终止时间T之前实际上是没有交易的.PE基金的这个非流动性特征有两个主要的含义,1)PE基金的股份不能像股票或债券那样可以在二级市场即时购买.相反,作为有限合伙人(LP)的投资者首先作出一个资本承诺,然后,在后续的时间里,作为对资本募集的回应将投入特定数量的资金给基金(也称为资本提取).这些资金承诺是不可逆的,而且,通常在资金承诺给基金的时间和资金实际被基金提取用于投资的时间之间有很大的滞后;2)PE基金的现金分红(也称为资本分配)不能立即再投资于基金,同时,这些现金分红是很重要的,因为PE基金的生命周期是有限的[19].

基于上述原因,投资者不能像经典Merton投资组合模型中那样,可以动态地选择持有PE基金的比例,而只能随着时间的推移,选择他们对基金的新的资本承诺数量.考虑到PE投资的这个特殊性,本文假设投资者从其总投资组合Pt的当前值中按一定的比例连续的承诺资金给PE基金.若记Ct为投资者在t时刻未被提取的承诺资金,则有

式(4)中的第一项(Ptvtdt)表示在t时刻投资者从其总投资组合Pt中以比率vt连续的做出资本承诺.参数vt是投资者的承诺比率,也是模型的第一个决策变量.需要指出的是vt是严格非负的,因为对PE基金做出的资本承诺是不可逆的.式(4)中第二项(−Ctδdt)反映了承诺资本是逐渐地被提取并投资于PE基金的事实,这里假设PE基金是以某个固定的非负比率δ从剩余的未被提取的承诺资本Ct中进行资金提取.参数δ反映了市场中PE基金的(平均)提取比例,在模型中是一个不能由投资者控制的外生变量.

2.3 投资组合的动态过程

为了定义投资组合的动态过程,假设承诺资本Ct在实际被PE基金提取之前,可以投资于股票和债券,并且PE基金的资本分红可以被再投资于股票和债券.令Lt表示在时刻t投资于股票和债券的流动财富,并假定投资者将流动财富Lt的比例投入股票,而将的比例投入债券.同时,令It表示在时刻t投资于PE基金的非流动财富.

上面的假设生成一个Lt和It的资金循环流,可以由下面的方程组描述

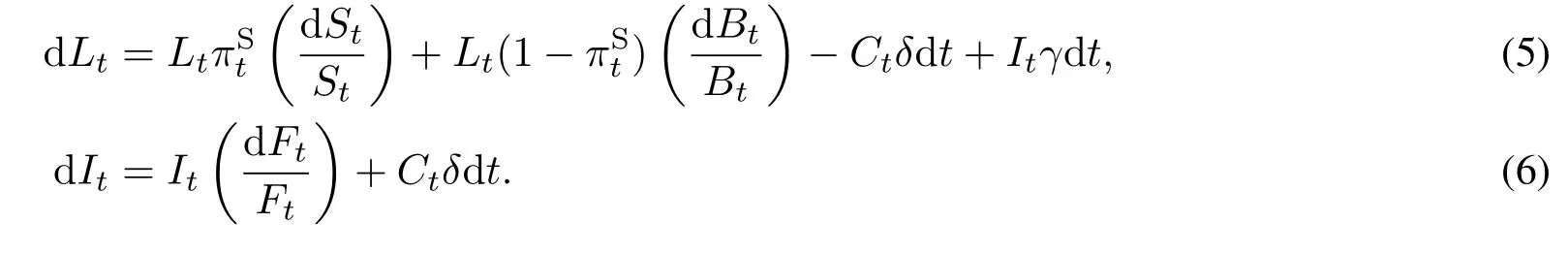
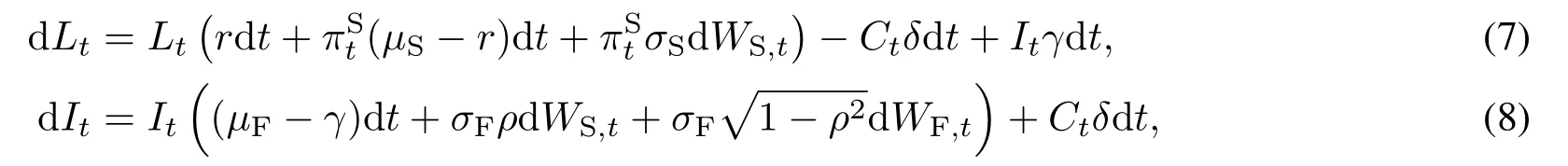
根据式(7)和式(8),即可给出投资者的总投资组合Pt=Lt+It的价值动态方程

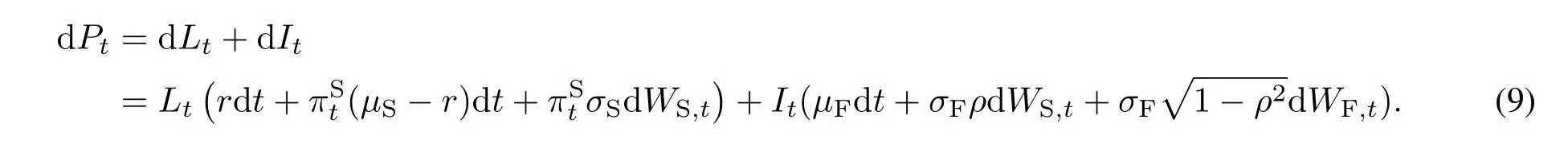
3 考虑后悔厌恶的行为投资组合优化

3.1 后悔厌恶型投资者的投资组合决策问题

考虑一个有限理性的、基于后悔厌恶行为的投资组合决策问题.投资者的目标是最大化某个终端时刻T的期末财富PT对应的期望效用.具体地,投资者的决策问题是寻求最优投资比例和资本承诺策略ˆv(t),使得下列目标函数达到最大,即

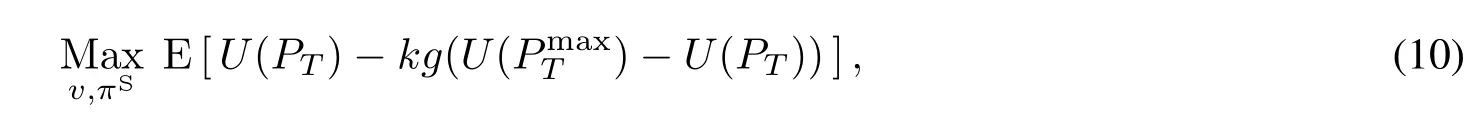
满足如下动态过程

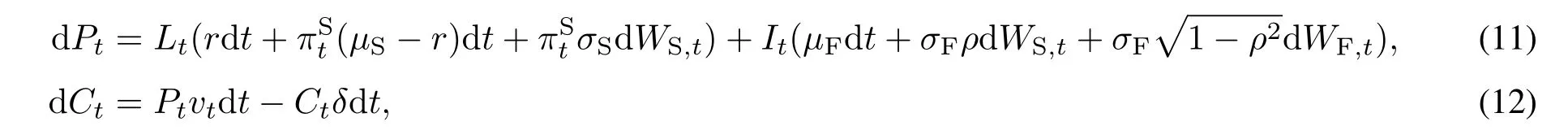
和约束条件

其中效用函数U(p)=pα/α,α＜1,α̸=0且1−α为投资者的相对风险厌恶系数.g(·)是一个严格单调增加的凸函数,反映了投资者的后悔厌恶行为[8,9],k＞0表示投资者的后悔厌恶程度.

当k=0时,模型(10)的目标函数即为传统的CRRA效用.由于g(·)是严格单调增加的凸函数,本文选取后悔函数为g(x)=xθ/θ,且θ＞1.

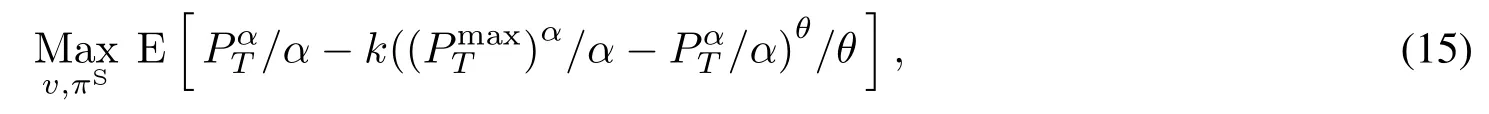
满足动态过程和约束条件式(11)∼式(14).

问题(11)是一个跨期投资组合问题,这类问题也称为随机最优控制问题.投资组合财富过程Pt称为状态过程(或状态变量),资本承诺比率v(t)和股票投资比例πS(t)称为控制过程,条件vt≥0是一个控制约束,以确保对PE基金的资本承诺是严格非负的.

3.2 求解投资组合优化问题

求解连续时间投资组合问题的经典方法是由Merton[15]提出的随机动态规划,或者由Cox等[20]提出的鞅方法.遗憾的是,这些方法并不能直接用于求解最优控制问题(15)的解析解.一般来说,动态投资组合选择问题仅在投资者的偏好与资产收益动态过程的某些特殊参数化情形才可以获得解析解.

随机模拟技术也可以用于给出动态投资组合问题的数值解.例如,Kraft等[21]应用Monte Carlo模拟求解连续时间生命周期最优住房、消费与投资决策问题.由于本文的目的是对包含PE基金的动态投资组合问题给出一个容易实施的求解策略,借鉴文献[1]的思路,本文采用不同于文献[18–21]的方法求解最优控制问题(15).

首先,假定投资者可以连续地交易三种资产.在时刻t,记wBt表示投资于无风险债券的比例,wSt表示投资于风险股票的比例,wIt表示投资于PE基金的比例.在可以连续再调整的假设下,则问题(15)退化为投资者通过动态地选择三种资产的投资比例最大化期末财富的期望效用.

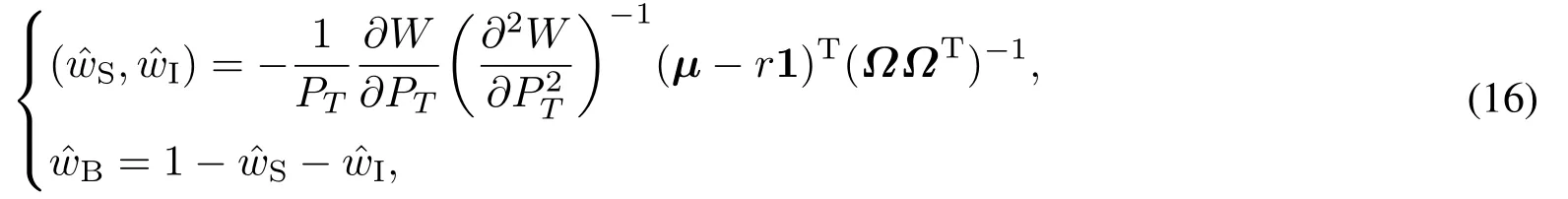
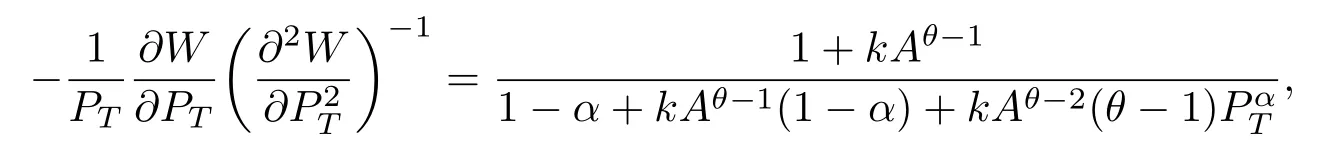
经过化简有

因此,若给出参数r,µS,µF,ρ,σS,σF,k,θ以及α的具体数值,便可以求出相应的最优投资比例以及从式(17)和式(18)的化简结果不难发现最优投资权重并不依赖于时间t,这意味着最优投资策略是不断地再调整投资组合,使得三种资产的投资比例保持不变.

然而,由于PE基金的非流动性,投资者并不能动态地选择投资比例wI,因此不可能对投资组合的头寸不断的进行再调整,以使得对三种资产的投资比例不随时间发生变化.为解决这一问题,假定投资者采用一种短视的投资组合法则,试图使投资比例尽可能地接近忽略非流动性影响所获得的最优比例和下面通过两个步骤来推导出最优投资策略.

首先,由于投资者可以连续地调整持有股票和债券的流动性财富,通过式(16)定义流动财富中持有股票的最优比例为

式(19)意味着投资者将其流动性财富Lt以固定的比例ˆπS投资于股票,而将剩余的比例投资于无风险债券.

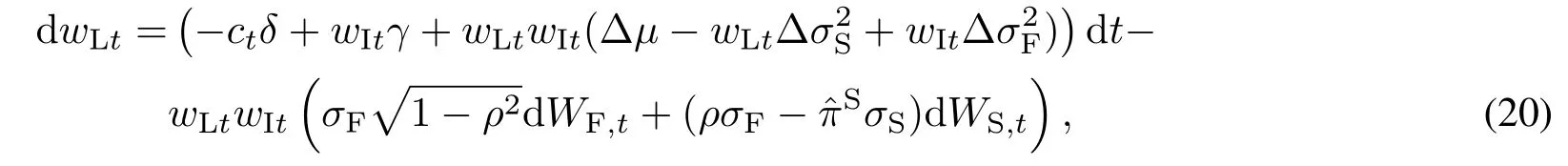
方程(20)表明投资组合比例wLt随着时间的变化而随机地发生变化.投资者可以通过改变对PE基金的比例承诺ct来部分地影响wLt的动态过程.假设投资者以∆t的频率做出新的资本承诺,类似于文献[1]的思路,本文采用条件最小二乘法(CLS)[22]来确定对PE基金的最优比例承诺ct.该方法的基本思想是,投资者的最优策略是选择t时刻的比例承诺ct,使得目标投资比例与n个未来离散时间点t+∆t,t+2∆t,...,t+n∆t(∆t＞0)上的流动资产投资比例在t时刻的条件期望的误差平方和最小.即求解下面的最优化问题

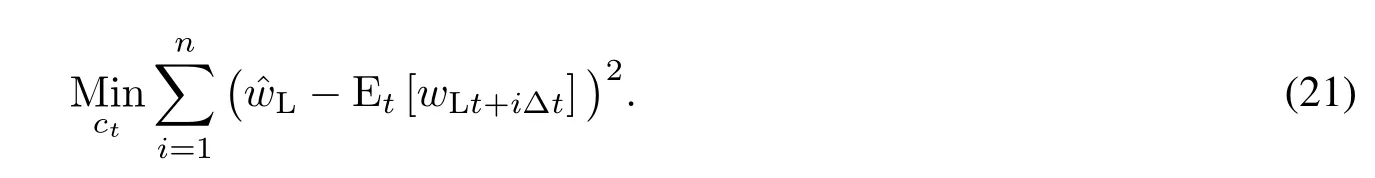
该目标函数考虑了在t时刻的承诺资金不仅会影响在t+∆t时刻投资于流动资产的比例,同时也会影响在未来的离散时间点t+2∆t,t+3∆t,...,t+n∆t对流动资产的投资比例.

根据附录B,求解优化问题(21)可以得到最优比例承诺为

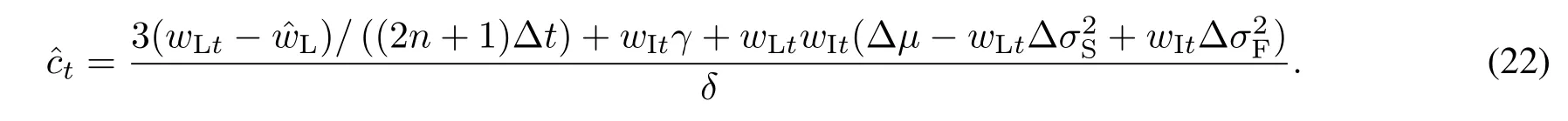
由方程(23)即可求出年度化的最优承诺比率为

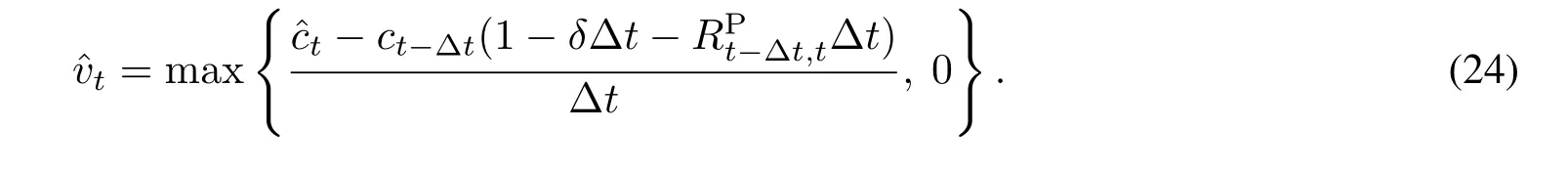
由于ct−∆t(1− δ∆t−是投资者在时刻t做出新的承诺之前尚剩余的比例承诺资本,方程(24)可以解释为,如果投资者的剩余比例承诺资本低于最优水平则其将对PE基金做出新的承诺,而如果剩余比例承诺资本超过了最优水平就不会做出新的承诺.

上面的推导给出了一个容易实施的动态投资与承诺策略,即投资者可以根据式(19)对流动性股票和债券以及根据式(24)对PE基金的承诺资本之间进行最优的资本再调整.

此外,将式(22)代入投资组合权重的动态过程式(20),可以得到下面的随机微分方程

过程(25)给出了wLt的均值–回复性质.参数κ控制投资比例wLt回复到其长期目标权重ˆwL的速度,σS与σF是该过程的波动参数.

4 数值模拟

在本节中,将通过数值模拟验证投资组合模型的合理性.首先,假定股票和PE基金具有相同的收益–风险特征,对由式(19)给出的流动性资产投资比例和由式(24)所给出的PE基金动态承诺策略进行数值模拟,考察当股票和PE基金的收益具有不同的相关性水平时,后悔厌恶型投资者和CRRA型投资者的最优投资组合策略与期望财富的变化情况.其次,考察当股票和PE基金具有不同的收益–风险特征时,两种不同偏好类型的投资者的最优投资组合策略与期望财富的动态变化过程.

4.1 参数选取

借鉴文献[1,5]的方法,本文选取参数使得对非流动性PE基金的投资可以解释为对PE的细分市场如并购(buyout)与风险投资基金(VC)进行分散化投资,而对股票的投资则解释为对股票市场指数的投资.

首先,根据文献[23–25]的研究,本文假设可交易的风险股票与流通受限的PE基金具有相同的收益率和波动参数,并根据Ang等[5]的估计结果,选取如下参数µS=µF=0.12,σS=σF=0.15.这种参数取值方法的一个优点是它可以将非流动性对投资组合的影响与可能是由于两种风险资产具有不同的Sharpe比而获得的结果区分开来.然后,再考察当股票和PE基金具有不同的Sharpe比时投资组合策略的变化情况.

借鉴文献[1]的研究结果,选取资金提取比率δ和现金分红比率γ的参数值分别为δ=0.52,γ=0.22.类似于文献[1,5]的参数取值方法,在CRRA情形,令相对风险厌恶系数为1−α=6,同时,取无风险利率为r=0.04.

进一步,假设投资期限为10年且∆t=0.25,n=12.即假设投资者在每个季度会对PE基金做出新的资本承诺,并且当决定最优承诺比率时,考虑这些承诺资金对接下来的12个季度的投资组合权重的影响.此外,假设投资者的后悔厌恶参数k=5,且θ=2.

4.2 投资组合权重的动态过程

假设I0=0,C0=0,且设风险股票与PE基金的收益率相关系数ρ=0.6,即假设两种风险资产的收益率具有较高的相关性,下面的图1给出了后悔厌恶型投资者对流动资产(股票和债券)与非流动资产(PE基金)的平均投资权重的动态变化过程,其中实线表示平均的资产投资权重,虚线之间的区域表示95%的置信区间.以下结果是通过Monte Carlo模拟迭代10 000次生成的,Monte Carlo模拟的详细过程可参见附录C.

与只包括股票和债券的Merton投资组合问题不同的是,当非流动的PE基金增加到投资组合中时,一个主要的结果是对所有资产的投资权重变为随机的,并且会随时间的变化而大幅变动.由于不可能对PE基金的投资进行连续的调整,因此,投资者每季度对流动资产和非流动资产的投资权重都在一定范围内波动.

为了考察当股票的收益率与PE基金的收益率不相关或为负相关时,投资组合权重的变化情况,下面的图2和图3分别给出了取ρ=0和ρ=−0.2时,后悔厌恶型投资者对流动资产(股票和债券)与PE基金的平均投资权重的动态变化过程.类似地,以下结果也是通过Monte Carlo模拟迭代10 000次生成的.

图1a 流动资产的平均权重(ρ=0.6)Fig.1a Average weight of liquid assets(ρ=0.6)

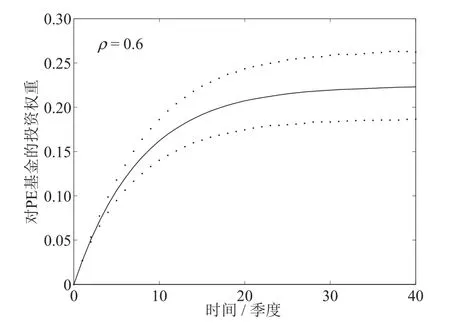
图1b PE基金的平均权重(ρ=0.6)Fig.1b Average weight of PE fund(ρ=0.6)

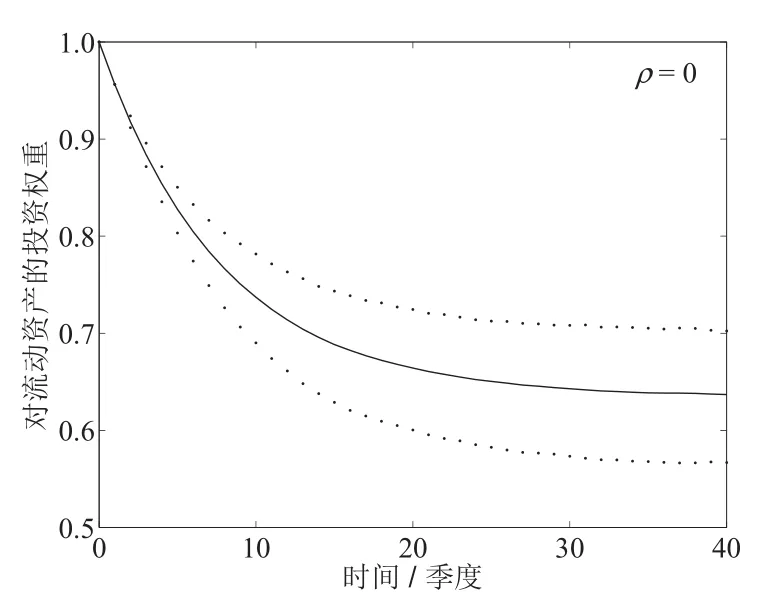
图2a 流动资产的平均权重(ρ=0)Fig.2a Average weight of liquid assets(ρ=0)

图2b PE基金的平均权重(ρ=0)Fig.2b Average weight of PE fund(ρ=0)

图3a 流动资产的平均权重(ρ=−0.2)Fig.3a Average weight of liquid assets(ρ= −0.2)

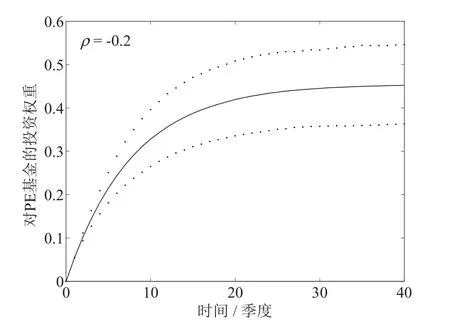
图3b PE基金的平均权重(ρ=−0.2)Fig.3b Average weight of PE fund(ρ= −0.2)

对比图1与图2,图3,可以发现,当股票收益和PE基金收益的相关性由正变为负时,后悔厌恶型投资者投资于股票和债券的平均比例逐渐降低,而对PE基金的平均投资比例则逐渐增加.这表明,相对于ρ为非负的情形,当ρ＜0时,后悔厌恶型投资者会更加偏好对PE基金的投资.

4.3 最优承诺策略

下面的图4,图5和图6分别给出了当股票收益率与PE基金收益率的相关系数为0.6,0,−0.2时,后悔厌恶型投资者与CRRA型投资者对PE基金的最优承诺比率vt的动态变化过程,其中实线表示平均承诺比率vt,虚线之间的区域表示95%置信区间.

图4a 后悔厌恶型承诺比率的动态变化(ρ=0.6)Fig.4a Dynamic change of regret aversion type commitment rate(ρ=0.6)

图4b CRRA型承诺比率的动态变化(ρ=0.6)Fig.4b Dynamic change of CRRA typecommitment rate(ρ=0.6)

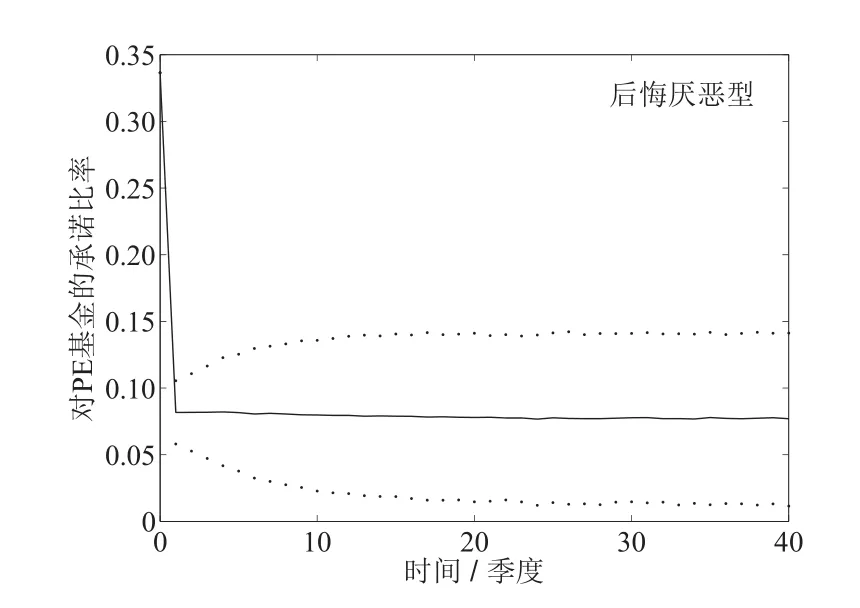
图5a 后悔厌恶型承诺比率的动态变化(ρ=0)Fig.5a Dynamic change of regret aversion type commitment rate(ρ=0)

图5b CRRA型承诺比率的动态变化(ρ=0)Fig.5b Dynamic change of CRRA type commitment rate(ρ=0)

图6a 后悔厌恶型承诺比率的动态变化(ρ=−0.2)Fig.6a Dynamic change of regret aversion type commitment rate(ρ= −0.2)

图6b CRRA型承诺比率的动态变化(ρ=−0.2)Fig.6b Dynamic change of CRRA type commitment rate(ρ= −0.2)

4.4 投资组合财富的变化

不失一般性,设P0=1,下面的图7给出了后悔厌恶型投资者与CRRA型投资者的最优投资组合所对应的累积期望财富Pt的动态变化过程.

从图7可发现,1)后悔厌恶型投资者的最优投资组合所获得的终端财富低于CRRA型投资者的最优投资组合所获得的终端财富;2)当股票与PE基金的收益率相关性由正变为负时,两种类型的投资者的最优投资组合所获得的累积期末财富也都由低到高逐渐增加.

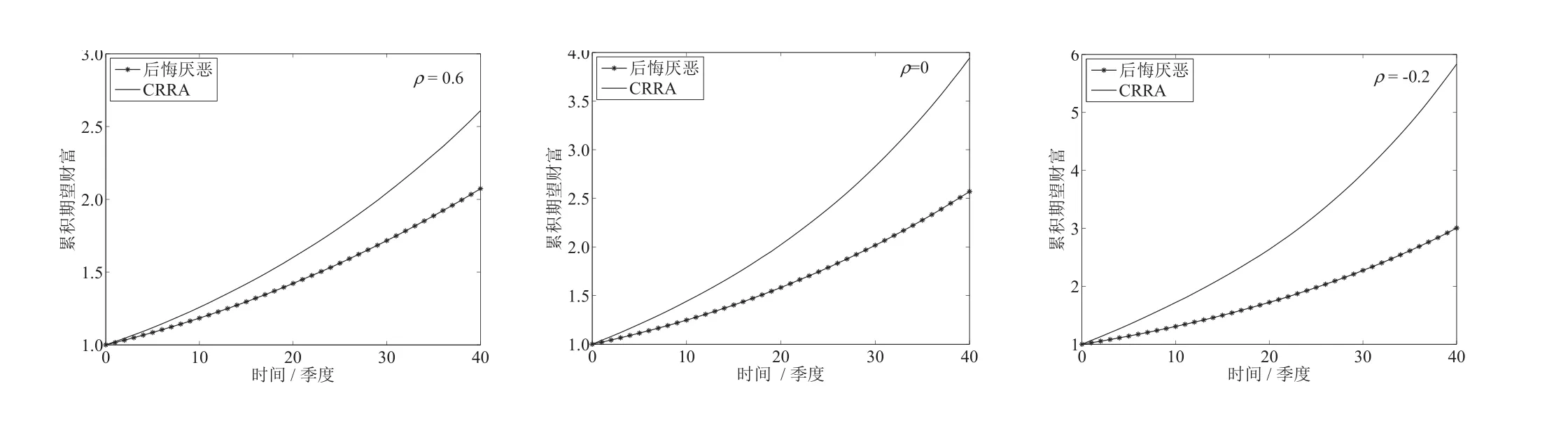
图7 累积财富动态(ρ=0.6,0,−0.2)Fig.7 Accumulated wealth dynamics(ρ =0.6,0,−0.2)

4.5 不同收益–风险特征的影响

为进一步考察当股票和PE基金具有不同的收益–风险特征时,最优投资组合策略的动态变化,参照文献[1]的方法,取µF=0.2＞µs=0.12,这意味着PE基金的Sharpe比是股票的Sharpe比的两倍.下面的图8给出了后悔厌恶型投资者和CRRA型投资者对PE基金的最优承诺比率的动态变化过程.从图8不难看出,对不同的相关系数ρ,后悔厌恶型投资者对PE基金的资本承诺比率均低于CRRA型投资者对PE基金的资本承诺比率.

此外,对µF=0.2,µs=0.12,经计算发现,当股票和PE基金的收益率相关性分别为0.6,0和−0.2时,后悔厌恶型投资者所获得的期末财富均低于CRRA型投资者所获得的期末财富,与4.4节的结论相似,这里就不再给出详细的结果.

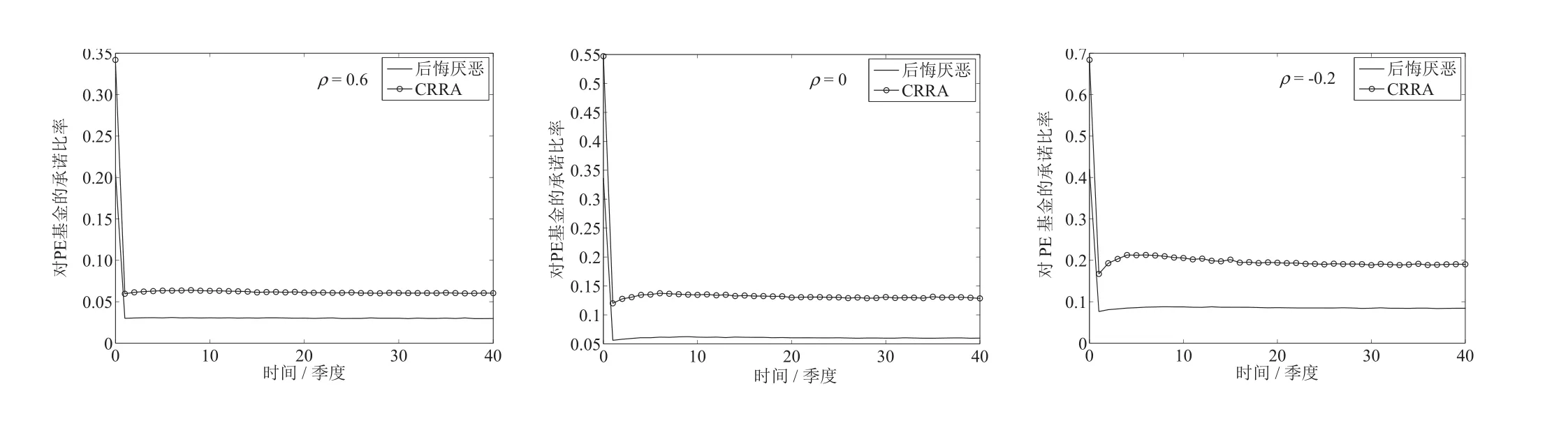
图8 承诺比率动态(ρ=0.6,0,−0.2)Fig.8 Commitment rate dynamics(ρ =0.6,0,−0.2)

5 结束语

借鉴行为经济学的后悔厌恶理论,在经典的Merton投资组合框架基础上,建立了同时考虑具有非流动性的PE基金和投资者后悔厌恶心理的三资产连续时间投资组合优化模型.本文通过提供一个动态承诺策略,给出了考虑PE基金的这些特殊特征的求解方案.模型的求解结果使我们可以直接考察PE基金的非流动性和投资者的后悔厌恶心理对最优资产配置与投资组合财富的影响,对当前关于PE基金的收益和风险特征的持续讨论具有重要的意义.此外,本文的求解方法也可以进一步推广到其他的具有资本承诺和期中资本分配的非流动性资产类,例如特殊的房地产、基础设施基金等[1,5].

本文只考虑了投资者的投资组合决策问题,由于实际中投资者不仅要进行投资决策,还要做出消费决策.因此,分别从传统CRRA型和后悔厌恶型投资者的视角出发,构建同时考虑投资与消费的连续时间动态投资组合模型,并设计有效的全局优化算法将是值得继续深入研究的问题.另外,本文假定PE基金的价值过程服从几何布朗运动,一个自然的推广是通过在PE基金的价值动态方程中加入跳跃或随机波动,使PE基金的收益率分布偏离正态分布,然而这通常只能以牺牲容易处理的解析解作为代价.