基于实时三线标定的车辆视觉定位方法*

李玉婷 胡钊政 黄 刚 刘国忠

(1.河北工业大学电子与信息工程学院 天津 300401；2.武汉理工大学智能交通系统研究中心 武汉 430063)

0 引 言

随着智能交通技术的飞速发展，汽车驾驶正逐步走向辅助化，而对车辆的精确定位是实现辅助驾驶的关键技术之一[1]。车辆在行驶中对其定位也就是对车辆位姿的计算，车辆位姿对车道保持[2-5]和自动换道[6-7]方面有重大意义。传统方法中车辆的定位信息大多由雷达、红外传感器、GNSS/IMU等高精度传感器获取[8]，成本较高，不利于车辆定位技术的推广。王楠等[9]提出了基于视觉传感器的ADAS纵向行驶工况识别方法，将车辆跟踪测距与车道线跟踪检测方法相结合以此来对车辆纵向行驶的工况进行识别。A.Rae等[10]在GPS车辆定位中引入了视觉特征，降低了车辆在街道交叉口的定位误差，但对于交叉口以外的位置未能实现完整的定位。徐美华等[11]提出的车辆偏离决策，利用车道线的对称性，基于角度判断车道偏离情况。由于车载摄像机采用预先标定算法，无法避免车辆震荡以及路面环境变化带来的影响。然而上述2种车辆视觉定位方法都预先对车载摄像机进行了标定，导致车辆在运动中的位姿计算精度受到较大影响，且上述方法未能精确的计算车辆的位姿信息。特别是，车载摄像机的外参数容易受到车辆震动、颠簸和路面环境的影响，致使车辆位姿计算的精度较低。为解决车载摄像机实时标定问题，Lu等[12]提出了在城市交通场景下车载摄像机校准的算法，该算法通过计算曼哈顿方向的标志物实时校正车载摄像机的外参数。由于该算法需要3个曼哈顿方向的三维线，当遇到标志较少的路段时该算法将会失效。Tsung-Yu[13]等提出了基于Android的车道偏离预警方案，该方案通过车载图像的中间线检查车道偏离情况来做出警告。该方案无法实际计算出车辆偏离车道的距离，且未考虑车辆与车道线存在偏转角度的情况。李祎承等提出一种基于GPS与图像融合的智能车辆定位算法[14]，以计算车辆当前位置距离视觉地图中最近一个数据采集点的位姿为目标，故大量的视觉地图库是计算得到车辆当前车辆位姿的基础，该算法工作量较大。

由上述文献可知，现有的车辆定位方法不是定位精度较低，就是工作量较大。车载摄像机外参数易受到车辆振动颠簸和路面环境的影响，故车辆行驶中车载摄像机外参数标定不准会造成车辆定位精度低。因此，若能寻找一种适应车辆震动以及路面变化，且基于车道共有标志物的车载摄像机标定方法，即可对车辆实现高精确定位。笔者研究了基于实时三线标定的车辆视觉定位算法，首先利用车道共有标志物──车道线，基于三线标定法[15]实时标定车载摄像机的外参数，再利用实时标定结果以及射影几何和消失点原理对车辆进行定位，获取车道偏离距离和车辆偏转角度信息。

1 车辆定位算法

车辆定位的框图见图1，根据车载摄像机实时传输的视频数据，首先采用基于概率霍夫变换的快速车道线检测方法[16-18]，检测出距离车辆最近的2条车道线；然后再选取其中的3条车道边缘线，利用三线标定法对摄像机外参数进行实时标定；最后利用计算机视觉方法实时计算出车辆在行驶过程中偏离车道线的距离以及车辆相对于车道线的偏转角度。笔者主要研究车载摄像机外参数的实时标定法，并通过计算车辆位姿实现车辆定位。车辆位姿是指车道偏离距离和车辆偏转角度。

图1 车辆定位框图Fig.1 The framework of vehicle positioning

1.1 三线标定法实时标定车载摄像机

车辆行驶中车载摄像机焦距不变，其内参数为定值，采用Zhang算法[19]获取车载摄像机的内参数。车辆在行驶过程中速度快、道路标志少，借助棋盘格等标志物对车载摄像机外参数进行实时标定变得不现实。为解决这一问题，笔者提出利用车道线来实时标定车载摄像机外参数，研究了基于三线标定法的车载摄像机外参数实时标定算法，解决了车辆行驶中车载摄像机外参数标定困难、实时性差的问题，使其受到车辆振动、颠簸和路面环境变化的影响减小了。

假定车道在一定范围内为平面，则近场车道线可近似视为直线。在可视范围内检测出的距车辆最近的2条车道线，由4条车道边缘线L1，L2，L3和L4组成，对应图2中的直线l1，l2，l3和l4。三线标定法仅需要3条车道边缘线,则从4条边缘线中选3条的原则是：前1帧中车辆偏向哪个方向，则选取哪个方向2条车道边缘线以及另一方向车道线的内侧边缘线。如车辆向右偏选取直线L1，L2和L3，车辆向左偏选取直线L2，L3和L4。下文以L1，L2和L3为例叙述。

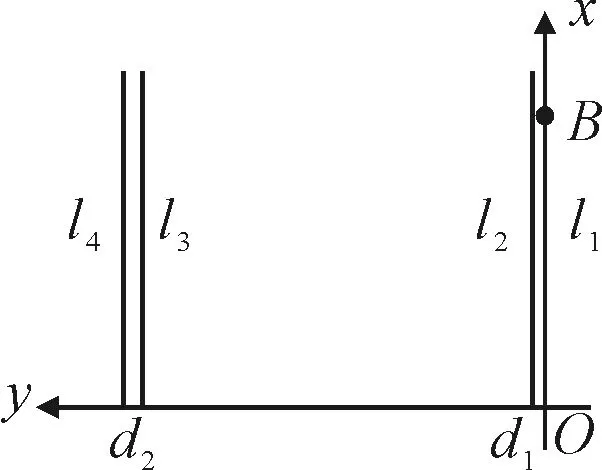
图2 公路水平面的坐标系Fig.2 Coordinate system of highway horizontal plane

在公路平面建立坐标系，见图3，x轴与最右侧车道边缘线L1重合，y轴位于公路平面且与车道线垂直。

图3 车载视频中的一帧Fig.3 One frame in the car video

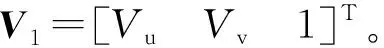
(1)

根据消失点V1可计算出车载摄像机外参数中旋转矩阵的x方向，表示为

n1=K-1V1

(2)

式中：K为车载摄像机的内参数矩阵。再根据射影几何的交比不变性，可求出另一个方向的消失点Va，见式(3)。

(3)

其中点m1，m2和m3如图2所示分别为直线l1，l2和l3上的点。由消失点Va可得na=K-1Va，n3=n1×na，故可计算出摄像机外参数中旋转矩阵的y方向，表示为

n2=n1×n3

(4)

由式(2)和(4)可得车载摄像机外参数的旋转矩阵

(5)

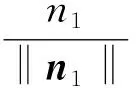
根据图3中原点O和图2中点o的关系可知

(6)

式中：t为车载摄像机外部参数的平移向量，H为单应矩阵。由l1，l2和l3与L1，L2和L3的对应关系可求得λ的值，将λ代入式(6)可求出摄像机外部参数的平移向量t。根据λ≥0可排除2个车载摄像机外参数的旋转矩阵R。由于R还剩余2种可能性，再在图像中确定一点b，使得b相对于世界坐标系中的x轴正方向的位置，可得

H-1b=B

(7)

由点B的x值为正，可唯一确定满足要求的车载摄像机旋转矩阵R。

1.2 车道偏离距离计算

车辆在行驶过程中，驾驶员可由车道偏离距离判断车辆是否超出安全边界。车道偏离距离为光心投影到路面的点到左车道线内侧边缘线的距离，范围为[-T1,T1+T2](T1为车道线的宽，T2为单车道的宽)。笔者基于视觉的算法对车道偏离距离进行计算，以此来获取车辆高精确的位置信息。基于视觉的车道偏离距离计算原理如下。

图4为车辆位姿的俯视图，直观的展示了车辆在行驶过程中位姿信息的情况。

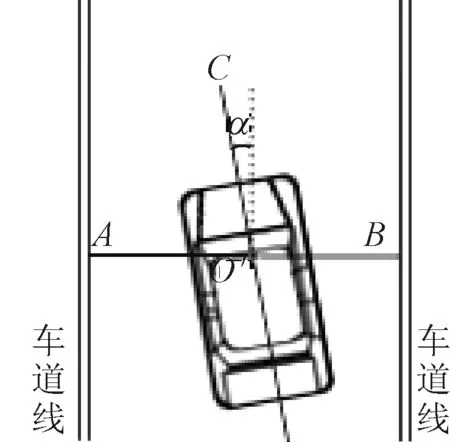
图4 车辆位姿的俯视图Fig.4 A top view of the vehicle′s position and posture

如图4所示，车道偏离距离为‖O′A‖，图像中车道边缘线的齐次方程可改写为见式(8)。

(8)

式中：k，b分别为车道边缘线的斜率和截距；u和v为图像坐标系中车道边缘线上某一点的像素值。设世界坐标系中车道边缘线表示为ax+by+c=0，由车载摄像机标定原理和式(8)可知

(9)

摄像机光心投影在地面的位置为点O′，将点O′的位置看做当前车辆的位置。最后求解点O′到车道边缘线距离，可求得行驶中车辆到车道线的距离，即图4中车道偏离距离‖O′A‖。当ki=0时O′C平行于车道边缘线且位于1条车道边缘线上，车道偏离距离为0，车辆偏转角度为0°。需要指出的是，上述计算的车道偏离距离可以经过转换，进一步计算出车轮距车道线的距离。

1.3 车辆偏转角度计算

在行驶中车辆发生偏转可直接导致车道偏离，致使车道偏离距离变化。若车辆偏转有助于车道保持、车辆趋向安全区域或车辆换道，则车辆偏转角对车辆安全驾驶起到积极作用，反之有消极作用，因此在车辆行驶中检测车辆偏转角度是必要的。车辆偏转角度为车身方向与车道线的夹角，范围为(-90°,90°]，当车辆左偏转时夹角为正数，右偏转时夹角为负数。当车辆单车道或跨道行驶时偏转角大多在[-30°,30°]范围内，当ki=∞时，O′C垂直于车道边缘线，车辆偏转角度为90°，车辆掉头时可达到。如图4所示，其中α为车辆偏转角度。笔者基于视觉的算法对车辆偏转角度进行计算，以此来获取车辆高精确的姿态信息。基于视觉的车辆偏转角度计算原理图见图5。

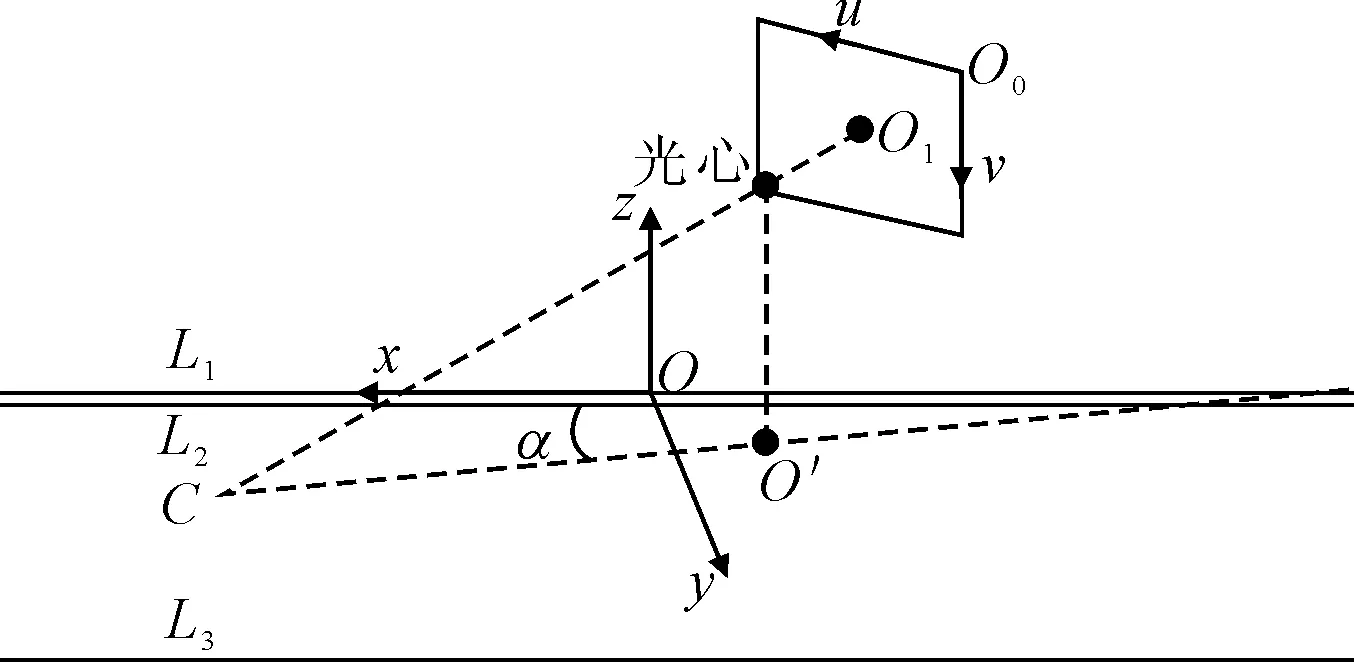
图5 计算车辆偏转角度原理图Fig.5 The schematic of vehicle deflection angle calculation

由摄像机的成像原理可知摄像机的光轴垂直于图像平面且交于点O1，点O1在图5中坐标为(u0,v0)，可利用单应矩阵H计算出光轴与路面的交点C的坐标。再根据三线标定法实时标定摄像机的外参数，计算车载摄像机在世界坐标系的位置

(10)

然后求得车载摄像机光轴到路面的投影O′C，O′C平行于纵向车身，即行驶中车辆的方向为O′C。最后求得O′C向量与x轴的夹角α，即为车辆偏转角度。

2 实验结果与分析

以下将主要从车载摄像机三线标定法与Zhang算法的对比、静态车辆定位实验和动态车辆定位实验3个方面对本文算法的效果进行反复验证。实验在两个不同路段，河北工业大学自强道(宽375 cm)和河北工业大学电子信息工程学院西侧车道(宽300 cm)，并将车载摄像机安装在不同的高度进行。实验中采集的图像和视频由车载摄像机拍摄，每帧图像尺寸为640×480(像素)，车载摄像机分别安装于车顶中心位置(高124 cm)和车辆后视镜位置(高97 cm)。首先利用Zhang算法对摄像机内参数进行预先标定，计算得到摄像机的内参数。其中，摄像机的焦距为532.3(像素)，主点位置位于[327.6 229.7](像素)。在以下实验中，车载摄像机内参数固定不变。受车道线检测效果的限制，实验的时段选取白天，避免雨雪天气。

2.1 三线标定法的精确性实验结果

三线标定法的精确性对车辆定位的精度起着决定性作用。实验中车载摄像机距路面的实际高为97 cm，棋盘格贴在路面，见图6。实验中分别利用三线标定法和Zhang算法标定车载摄像机的外参数及计算车载摄像机的高度。并对二者的实验结果进行对比，见表1，表明笔者提出的三线标定法标定车载摄像机外参数的结果精确。

图6 标定法对比实验Fig.6 Comparison experiment of different calibration methods

2.2 静态车辆定位实验结果

车辆静止时在白天不同时段多次采集路面图像，并使用米尺和经纬仪测量车道偏离距离及车辆偏转角度，与本文算法求得车辆位姿进行比较，以此判断本文算法的误差。

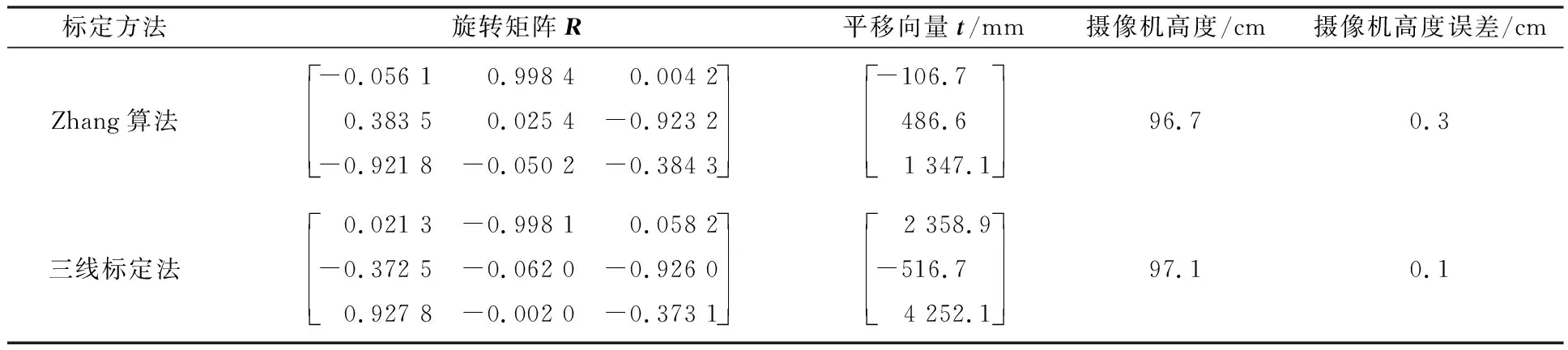
表1 标定法对比实验结果Tab.1 Comparison of calibration results from different methods

1) 车载摄像机安装的高为124 cm，车辆在宽375 cm车道进行实验。车辆在不同位姿时车载摄像机采集143张图像，图7为从中选取的7张图像，车辆偏转角分别为0°，10°，20°，25°，-10°，-20°，-25°。利用本文算法求得车辆位姿与实际测量值比较并计算误差，车辆定位的误差分布见图8。

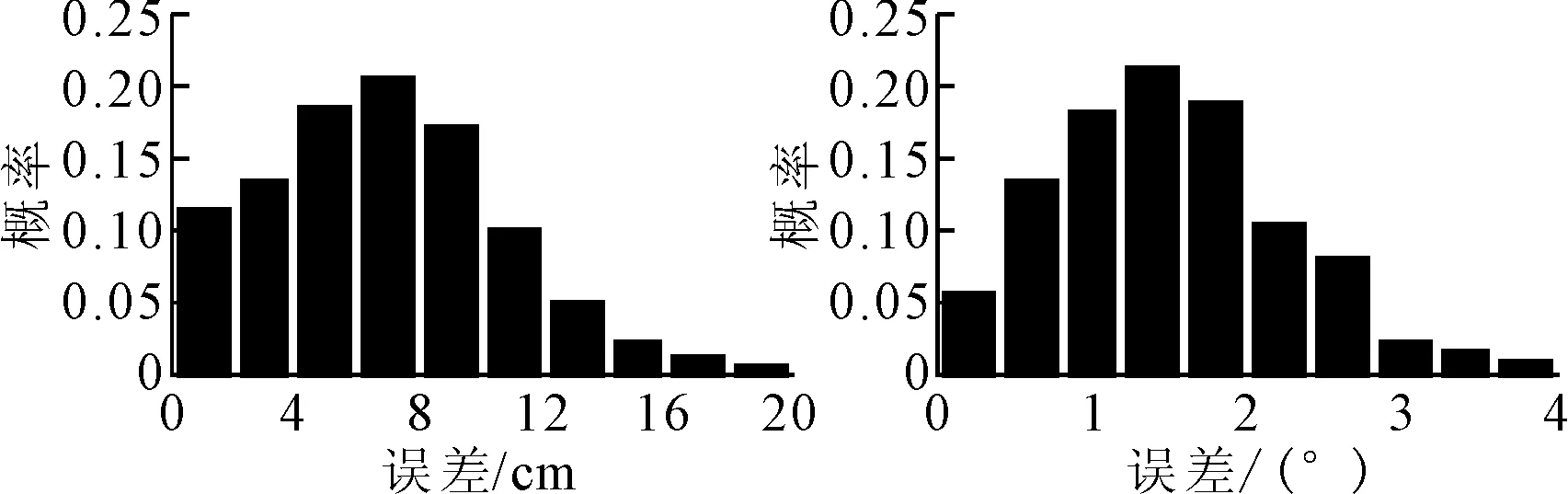
图8 车辆定位误差概率分布直方图Fig.8 Histogram of error probability distribution

由图8可知，本文算法计算出的车道偏离距离平均误差为6.9 cm，在0到14 cm范围内的误差占比95.7%；车辆偏转角度平均误差为1.5°，在0°～3.2°范围内的误差占比为97.6%。实验结果表明本文算法可满足智能车辆高精度的定位要求。

2) 安装的车载摄像机高97 cm，车辆在静态车辆定位实验1的同一车道进行实验，当车辆在不同位姿情况时车载摄像机采集156张图像来计算车辆位姿，图9为求得车辆定位的误差概率分布直方图。

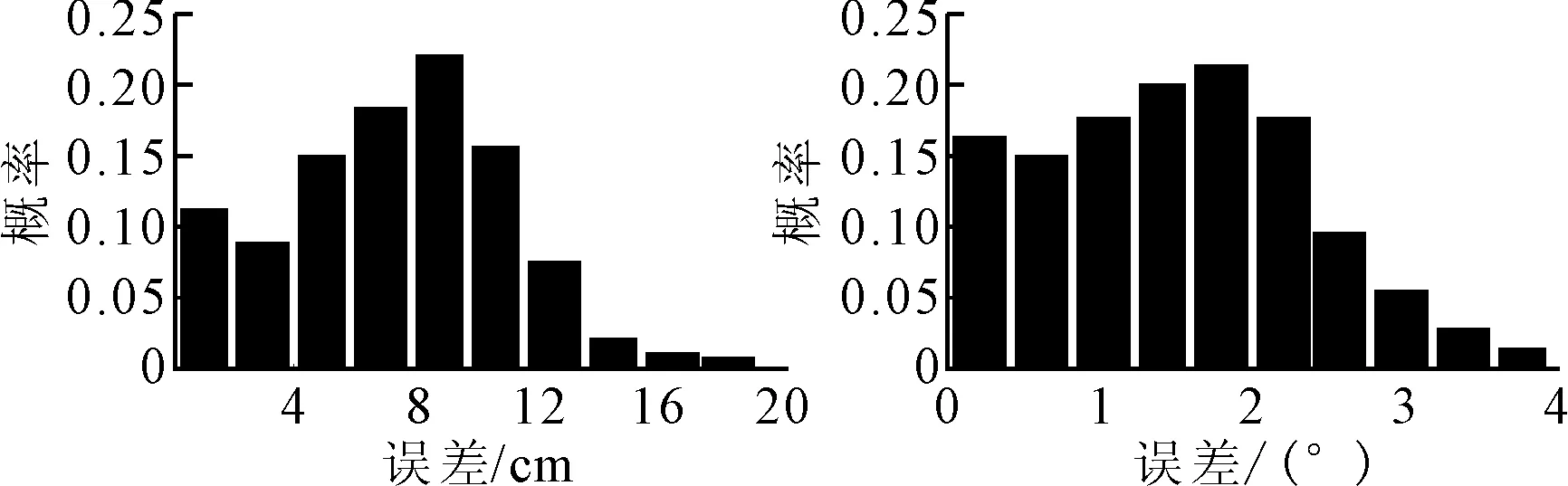
图9 车辆定位误差概率分布直方图Fig.9 Histogram of error probability distribution

由图9可知，本文算法得到的车道偏离距离平均误差为7 cm，在0到14 cm范围内的误差占比为97.7%，车辆偏转角度的平均误差为1.5°，在0°～3.2°范围内的误差占比为96.9%。将此结果与静态实验1对比，可知本文算法的定位性能受车载摄像机安装高度的影响，当车载摄像机安装高度适当提高时，车辆定位越更精确。

3) 车载摄像机安装高度为124 cm，实验场地车道宽为300 cm，实验中采集125张图像，求得定位误差概率分布直方图见图10。

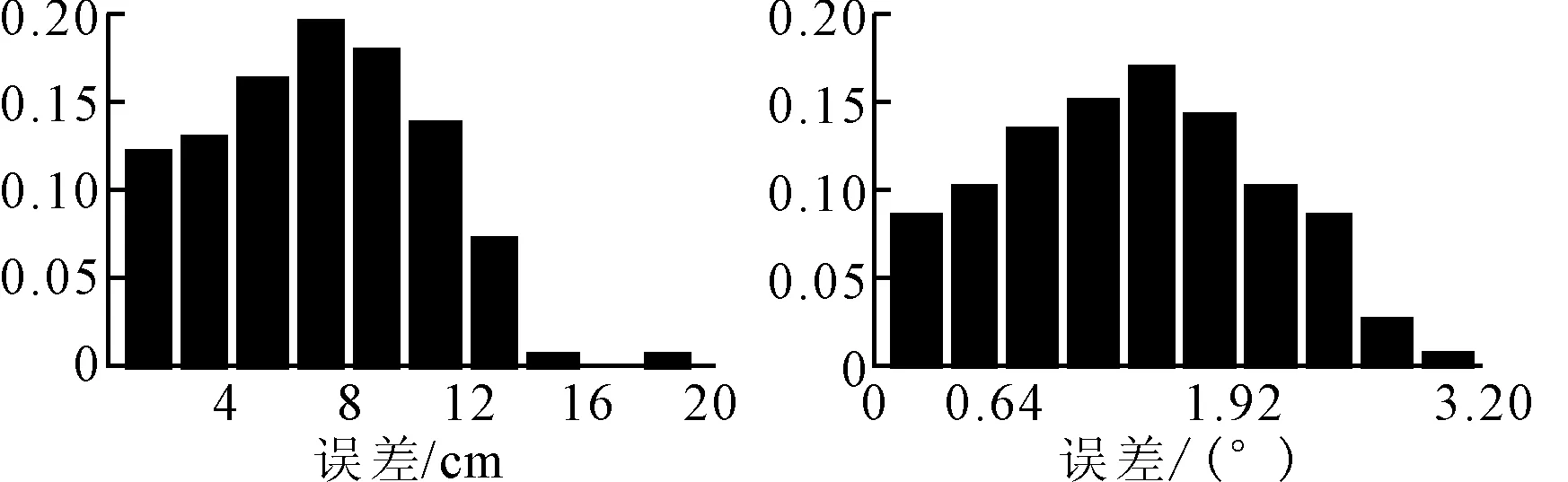
图10 车辆定位误差概率分布直方图Fig.10 Histogram of error probability distribution

由图10可知，车道偏离距离的平均误差为6.9 cm，在0到14 cm范围之内的误差占比为98.4%；车辆偏转角度平均误差为1.4°，在0°～3°范围之内的误差占比为99.2%。由静态实验1和3可知，车道越窄定位精度越高，该算法具有很强的适应性。

2.3 动态车辆定位实验结果

动态实验中车载摄像机安装的高度为124 cm，实验车道宽375 cm，车辆怠速行驶，车辆的实际位姿信息通过轨迹测量法获取。将激光测距仪放在公路左侧，其采集的数据可计算出左前车轮位置，进而可计算出车辆在公路上行驶的轨迹，显示车辆运动中的实际位姿。

1) 表2为7个拐点处三线标定法求得的车载摄像机外参数(旋转矩阵R和平移向量t)和图11为车辆行驶轨迹图，其中车辆偏转角度发生变化的7个地点称为拐点。

图11 车辆动态行驶轨迹Fig.11 Vehicle dynamic trajectory

计算出的摄像机高度。表3为7个拐点处车辆的定位结果。

表3 车辆动态定位结果Tab.3 Vehicle dynamic positioning results

由表2可知车辆行驶时车载摄像机外参数会因受车辆震动、颠簸和路面环境的影响发生变化，致使车载摄像机距路面的高度发生变化。例如，7次测量结果中，摄像机的平均高度为122.8 cm，而最大高度与最小高度相差可达4.1 cm，这会对车辆位姿的计算结果造成较大影响，上述实验结果也进一步证实了基于三线标定法实时标定车载摄像机外参数的必要性。

由表3可知本文车辆定位算法能高精度地计算车辆的位姿，车道偏离距离为7.3 cm和车辆偏

转角度为1.5°。

2) 为验证本文算法的有效性，将其与文献[11]算法进行比较，7个拐点处车辆定位误差对比结果见图12。

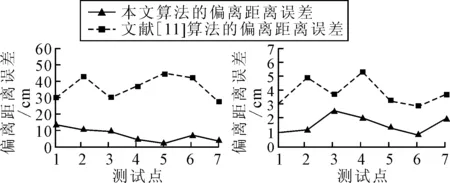
图12 车辆定位结果对比Fig.12 Comparison of vehicle positioning results

由于文献[11]算法通过预先标定算法确定摄像机的外参数，没有考虑车载摄像机外参数的动态变化，导致车辆位姿计算出现较大的误差。如图12所示，文献[11]算法计算的车道偏离距离误差高达45 cm，平均误差达36 cm。同时，计算的偏转角度误差最高达5.3°，平均误差为3.8°。而笔者提出的算法，通过实时三线标定车载摄像机的外参数，提高了车辆动态条件下的位姿计算精度。如图12所示，本文算法计算的车道偏离距离误差平均为7.3 cm，最大误差不超过13.4 cm，计算的偏转角度误差平均为1.5°，最大不超过2.5°。通过图12的实验结果对比，可以发现通过本文实时三线标定计算出来的车辆位姿更精确，算法性能明显优于预先标定的算法。

3 结 论

车辆在行驶过程中由于车体振动、颠簸及路面变化等实时变化状况给车载摄像机的外参数带来较大的变化，从而影响车辆位姿计算的精度。本文提出了一种基于三线标定的车辆视觉定位方法，实现在白天避免雨雪天气条件下基于车载视觉的车辆位姿计算。该算法通过三线标定法对车载摄像机进行实时标定，并以之为基础，提出了基于视觉的车辆位姿(车道偏离距离和车辆偏转角度)计算方法。实验中，无论是静态实验还是动态实验的结果都表明：本文算法在计算车辆位姿时精度高、适应性强、成本低廉，能够适应大多数路况和环境条件；能有效解决车辆动态变化引起的车载摄像机外参数实时变化问题，实现基于视觉的高精度车辆位姿计算，从而实现车辆精准定位。本文算法适用于光照充足的白天，在夜间场景下将会失效。为避免算法适应场景的单一性，将多传感器获取的数据进行融合，应用于车辆定位是未来的研究趋势。