藻类光竞争模型构建及水体紊动对竞争的影响
2018-07-26陈永灿刘昭伟中国水利水电科学研究院北京100038水利部防洪抗旱减灾工程技术研究中心北京100038西南科技大学环境与资源学院四川绵阳621010清华大学水沙科学与水利水电工程国家重点实验室北京100084
俞 茜,陈永灿,刘昭伟,李 娜 (1.中国水利水电科学研究院,北京 100038;2.水利部防洪抗旱减灾工程技术研究中心,北京 100038;3.西南科技大学环境与资源学院,四川 绵阳 621010;4.清华大学水沙科学与水利水电工程国家重点实验室,北京 100084)
在夏季等水华易爆发的季节,蓝绿色的聚集物常常会覆盖整个湖面.这种蓝绿色的聚集物一般为蓝藻水华.然而,这种现象却鲜少在水流湍急的河流中出现.一般情况下,河流起始端的浮游藻类藻浓度很低[1],不会出现水华,只有在水温适合且营养盐充足的大型河流的中下游河段才有可能出现[2-6],且形成水华的优势藻属通常为中心纲硅藻[7-8]或者绿球藻目绿藻[9]等河流型藻属.在自然界中,藻属不可能单独存在,而是多种藻属共同生存,互相竞争光强等资源[10-12].
光是藻类进行光合作用的重要能量来源,决定了藻类的初始生产力,当营养盐浓度充足,且水温一定的情况下,多种共存的浮游藻类会一起竞争光强,光强成为藻类竞争的唯一资源.此时,水体物理特征(例如,水体紊动)的改变可能影响共存藻类获得光强的情况,从而改变水体中的优势藻属[6,12-13].例如,滇池中占据优势地位的微囊藻在进入下游水流较为湍急的螳螂川后逐渐被绿藻和硅藻所取代[13].然而,水体紊动是如何干预藻类之间竞争光强并助其取得竞争优势的机理尚不清晰.
前期研究构建了微囊藻属浮力调节模型与移流扩散模型相结合的复合模型[14],模拟结果与实测数据吻合良好.但在自然界中,微囊藻属不可能单独存在,而是与其他多种藻属共同生存.微囊藻属虽然在紊动较弱的水体中易占据优势,但是在紊动较强的水体中却常常被小球藻属等硅藻或者绿藻所取代.因此,本文通过构建多种藻属之间的光竞争模型,模拟不同水体紊动情况下,藻类浓度的变化过程,以期解释水体紊动对于藻类竞争的干预机制.
1 数学模型和数值方法
构建的竞争模型的基本假设如下:(1)假设研究水体营养盐充足、温度适宜、浮游动物捕捉等导致的藻属损失为固定值[15],竞争藻属的生长速率在垂向只受光强影响;(2)假设水体垂向密度一致;(3)假设水体垂向紊动扩散系数一致;(4)假设微囊藻群体的浮力调节由单细胞通过光合作用/呼吸作用改变体内的碳水化合物含量控制,而小球藻属密度不变,下沉速度为固定值;(5)假设不同直径的微囊藻群体体内细胞体积占据群体总体积的比例不变,单细胞中伪空胞占据单细胞体积的比例不变;(6)假设研究的水体垂向水体密度不变,即暂时不考虑水体分层.选择微囊藻属作为具有浮力调节能力的藻类代表,选择小球藻属作为下沉型藻类的代表.
两种(多种)浮游藻类光竞争模型由以下3部分组成:(1)对流扩散方程[11];(2)微囊藻藻细胞组织密度改变模型[16];(3)静止水体中藻属上浮/下沉模型.竞争模型与前期研究[14]构建的微囊藻属模型的最大区别包括:(1)增加了竞争藻属下沉型小球藻属;(2)单藻模型中水体的消光系数为一个固定数值,而本文构建的竞争模型中竞争藻属的自遮蔽作用是随着浮游藻类垂向藻浓度分布而改变的动态函数.由于水体中存在两种(多种)浮游藻属,均会利用光强进行光合作用,而在竞争光强的过程中,除了自身遮蔽光强阻碍下层水体中藻属获取光强,还会遮蔽共存于水体中的其他藻属,阻碍竞争对手获取光强.
1.1 移流扩散方程
模型中竞争藻属的生长速率假设在垂向只受光强限制,遵循 Monod方程规律.藻属在垂向的迁移为自身上浮/下沉以及被紊动水体夹带两个作用综合的结果.式(1)~式(3)即为共存藻属在水深方向的移流扩散控制方程:
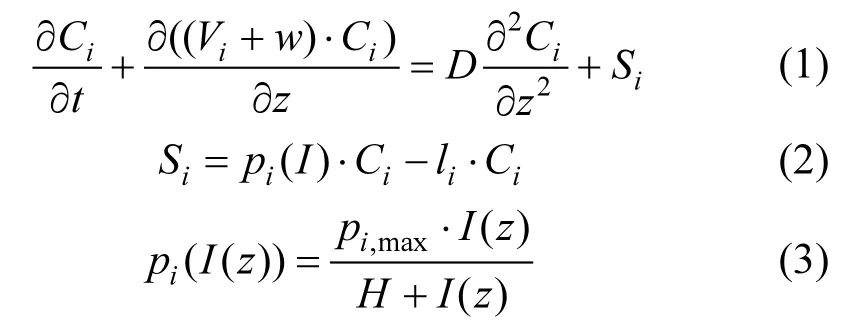
式中:i代表第i种竞争藻属,i=1,2,…,n;Ci为竞争藻属的垂向浓度,cells/L;Vi为竞争藻属自身在水体中的迁移速度(V>0,下沉;V<0,上浮),m/s;w 为水体垂向紊动流速,m/s;D为水体的紊动扩散系数/垂向涡旋系数,cm2/s;pi(I)是竞争藻属在光强为 I时的生长速率,1/h;li为竞争藻属的损失速率,1/h;pi,max为竞争藻属的最大生长速率,1/h;H为半饱和生长速率对应的光强,µmol photons/(m2·s).
1.2 随光强变化的浮力调节模型
小球藻属等下沉型藻属的密度不随光强的变化而变化,公式(4)为微囊藻属密度随光强的改变而变化的方程:
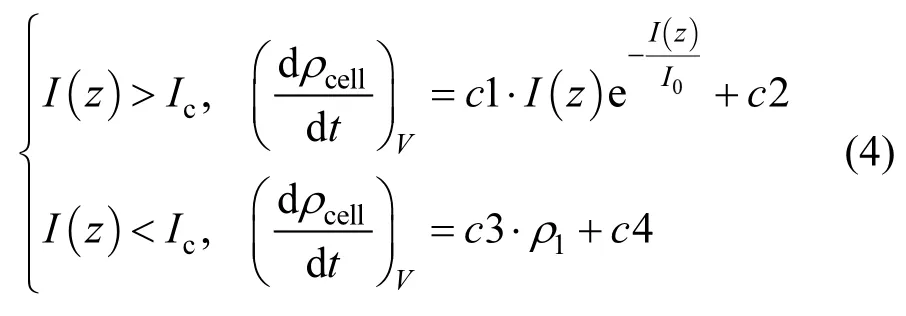
微囊藻属与小球藻属在水体中通过自遮蔽光强改变水体垂向光强分布的计算见下式:
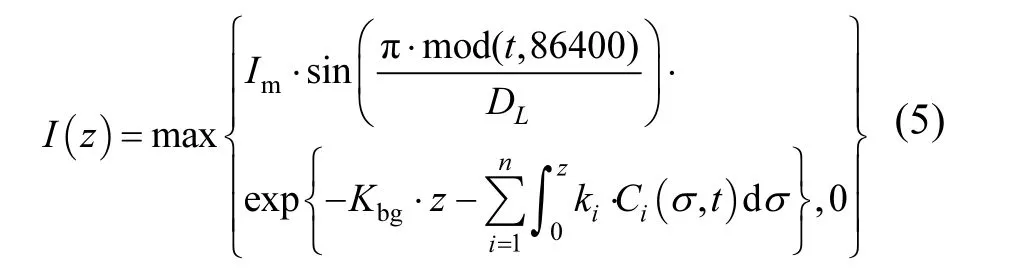
式中:Im为正午水体表面接受的最大光强,μmol photons/(m2·s);DL为光周期,s;Kbg为水体的背景消光系数,1/m;z为群体所在的水深位置,m;ki为第i种浮游藻属的消光系数,cm2/106cells, i=1,2,…,n.
1.3 静止水体中群体上浮/沉降模型
微囊藻群体和小球藻属均近似为球形,因此在静止水体中的上浮/下沉速度均可以采用在该领域被广泛应用的Stokes方程:
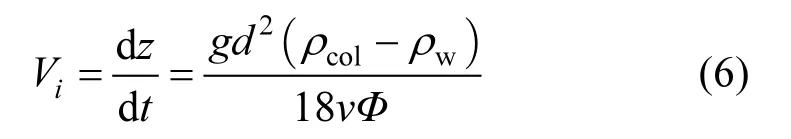
式中:g为重力加速度,一般取为 9.8m/s2;ρw为水体密度,kg/m3;ρcol为微囊藻群体密度,kg/m3;d为球形微囊藻群体直径,m;v为水体的粘滞系数,kg/(m·s);Ф 为群体形状系数.
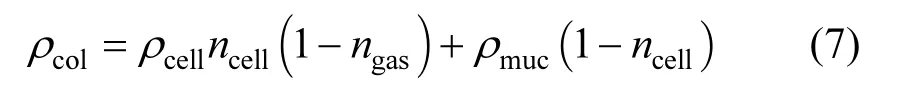
由于每个微囊藻群体都由黏液包围大量的内含有伪空胞的单细胞组成,因此微囊藻群体密度可由式(7)计算得到[17]:式中:ncell是微囊藻群体中细胞所占据的比例,%;ngas为单细胞中伪空胞所占据的比例,%;ρmuc为微囊藻属体内黏液的密度,kg/m3.
假设小球藻属的半径为 8µm,直接将小球藻属密度代入公式,计算得出本文中小球藻属的下沉速度为1.389×10-5m/s.
1.4 数值离散
采用全隐差分格式对上述控制方程(1)~(7)进行离散.同时,假设竞争藻属在水面和水底(z=0和 z=h)处无通量交换,给定如下水面和水底的边界条件:
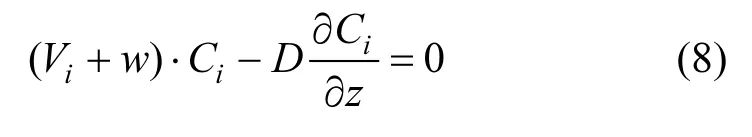
2 微囊藻属与小球藻属竞争分布
2.1 水体紊动对于微囊藻属和小球藻属垂向浓度分布的影响
研究人员在 1993年对位于荷兰阿姆斯特丹的Lake Nieuwe Meer进行了人工扰动,成功地将优势藻属由上浮型蓝藻转换为下沉型的硅藻[15].本文设置所有的参数与Lake Nieuwe Meer一致,假设竞争藻属的初始浓度在垂向分布均匀[15],模拟不同水体紊动情况下,微囊藻属和小球藻属的藻浓度垂向分布,分析研究最终的优势藻属.Lake Nieuwe Meer为超富营养化湖泊,平均水深为 18m,最深处水深为 30m,水面面积为1.3km2.其中,Lake Nieuwe Meer人工搅动前的水体紊动 D=0.17cm2/s,人工搅动后 D=5.1cm2/s[15].所有参数设置见表1,模拟结果见图1.
由图1(b)可知,人工扰动前,大量的微囊藻属集中在位于上层水体中的最大藻浓度处,垂向呈现非常明显的单峰分布,而竞争的小球藻属由于重力作用,整体下沉,主要位于水体底部.由于微囊藻属在垂向分布的巨大优势,因此,主要位于上层水体中的微囊藻属可以获取充足的光强并进行充分的光合作用,然后大量生长,促使上层水体中的微囊藻属浓度越来越高.同时,由于聚集在上层水体中的微囊藻属会阻碍光强入射,因此,在其下方运动的小球藻属由于缺少足够的光强,生长速率减缓,浓度显著减少.
而在动态水体中,水体垂向紊动扩散决定微囊藻属和小球藻属在垂向的分布都较为均匀,见图1(c),因此,两种竞争藻属获取光强的几率相似,但是因为小球藻属生长速率较快,所以小球藻属的藻浓度增加快于微囊藻属,小球藻属和微囊藻属均会阻碍光强入射,导致下层水体中的光强迅速衰减,因此下层水体中的微囊藻属和小球藻属的生长速率均减小,而水体的紊动扩散作用会将上层较多的藻细胞带入下层水体中,由于小球藻属在上层水体中藻浓度相对较高,因此垂向均匀后的小球藻属的平均藻浓度依然高于微囊藻属,如此反复,最终,小球藻属取得竞争优势.
此外,本文将初始微囊藻属藻浓度:小球藻属藻浓度分别改为10:1和1:10,模拟结果发现,当水深和垂向紊动扩散系数一定时,经过一段时间后,最终取得竞争优势的藻属不会改变.
综上,紊动较弱的水体中,微囊藻属的浮力调节能力导致大部分微囊藻属集中在上层水体中,而小球藻属在重力作用下,大多数位于底层水体,由于光强是两种藻属竞争的主要资源,位于上层水体的微囊藻属会获得极大的优势,并大量生长,最终取得竞争优势,即稳态水体中,藻类垂向自迁移运动是决定最终竞争优势藻属的主要因素.相较之下,动态水体中,紊动的垂向扩散系数促使所有藻属在垂向分布较为均匀,在获取光强的机会相似的情况下,生长速率成为决定藻类取得竞争优势的关键因素[20].

表1 文中所有参数取值Table 1 Parameters in the mathematical model
2.2 藻类自遮蔽对于竞争藻属浓度垂向分布的影响
目前许多专门研究藻类浓度垂向分布的模型均未考虑浮游藻类的动态自遮蔽,然而不考虑竞争藻属的自遮蔽很可能会对模拟结果产生较大影响并导致模拟结果与实测数据存在偏差.本文构建的浮游藻类光竞争模型和前期研究[14]中构建的微囊藻属单藻模型的一个重要区别为:竞争模型中加入了竞争藻属双方的动态自遮蔽,即竞争藻属对于入射光强的遮蔽作用不是一个固定值,而是随竞争藻属的藻浓度在不同时刻的垂向分布的改变而改变的一个函数.为了研究自遮蔽项对于竞争藻属藻浓度的影响,本文对比了加入和不加入自遮蔽项的情况下,共存的竞争藻属在水体中藻浓度垂向分布的情况.若竞争藻属的藻浓度较小,则浮游藻类自遮蔽导致的消光影响可能小于背景消光系数,因此,选取较大的初始藻浓度进行研究.假设初始微囊藻属藻浓度为 2×107cells/L,小球藻属初始藻浓度为5×107cells/L,且均沿垂向均匀分布,模拟这 2种藻属10d后藻浓度的垂向分布情况.所有参数设置见表1.较深的稳态湖泊(D=0.17cm2/s,水深= 18m)的模拟情况见图2,较浅的紊动河流(D=400cm2/s,水深=3m)的模拟情况见图3.
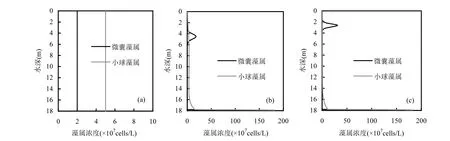
图2 紊动较弱的湖泊中微囊藻属和小球藻属竞争光强的模拟结果(D=0.17cm2/s,水深=18m)Fig.2 Model predictions of competitions for light between Microcystis and Chlorella in calm water (D=0.17cm2/s,Depth=18m)
对比图 2(b)和(c),在动态自遮蔽环境下,微囊藻属最大藻浓度比无自遮蔽项的藻浓度大,且微囊藻属最大藻浓度的位置明显高于无自遮蔽时的微囊藻属最大藻浓度位置;小球藻属藻浓度在有动态自遮蔽时明显小于无自遮蔽时的藻浓度.究其原因:当考虑浮游藻属动态自遮蔽时,水体中消光系数增加,由前期研究可知[21],消光系数越大,微囊藻群体运动的区域越靠近水面.而越接近水面,微囊藻属能获取的光强越强,进行的光合作用越充分,所以藻浓度增长更快.而下沉型小球藻属在消光系数较大且紊动较弱的水体中主要集中在下层水体,微囊藻属藻浓度的增加会导致消光系数增大,从而导致大量位于深层水体中的小球藻属所能获取的光强减小,因此生长速率减小迅速,当生长速率小于损失速率时,小球藻属藻浓度减小.而小球藻属藻浓度的减少又促进微囊藻属的生长.综上,紊动较弱的水体中,当考虑竞争藻属的自遮蔽情况时,微囊藻属藻浓度增长的更快,而小球藻属藻浓度减少的也更快,即优势藻属会更快地取得竞争优势.
在紊动的河流中,浮游藻类自遮蔽消光带来的影响更加明显.对比图 3(b)和(c),无自遮蔽时,小球藻属藻浓度增长非常快,10d之后的藻浓度几乎是初始值的30倍,达到1.44×109cells/L,而微囊藻属藻浓度减少了约五分之一.当有动态自遮蔽存在时,单独生存的微囊藻属和小球藻属藻浓度都会受到抑制,与实际情况更吻合,因为在湍急的河流中,通常不会爆发水华,也较少有浮游藻类大量繁衍的情况出现.当竞争藻属共同存在于水体中时,由于小球藻属对微囊藻属的遮蔽作用,导致微囊藻属藻浓度减少更多.即加入浮游藻类的自遮蔽作用,消光系数增加后,微囊藻属和小球藻属的生长速率受到的限制更多,在此情况下,微囊藻属藻浓度减少的更快.

图3 紊动剧烈的河流中微囊藻属和小球藻属竞争光强的模拟结果(D=400cm2/s,水深=3m)Fig.3 Model predictions of competitions for light between Microcystis and Chlorella in turbulent water (D=400cm2/s, Depth=3m)
3 结论
3.1 微囊藻属和小球藻属分别在紊动较弱的水体和紊动较为剧烈的水体中取得竞争优势,根据数值模拟的结果分析,藻属的垂向自迁移能力以及生长速率分别是具有浮力调节能力的微囊藻属和生长速率较快的小球藻属在稳态和动态水体中取得竞争优势的关键要素.水体紊动较弱时,藻属的自由迁移决定了其在水体中的垂向分布,具有浮力调节能力的微囊藻属大量聚集在水体上层,进行充分的光合作用,易取得竞争优势;当水体紊动不断增大,紊动的水体会将藻类带至各水深处,导致所有藻类在垂向分布均较为均匀,此时,所有藻属获取光强的机会相似,因此,生长速率更快的小球藻属易取得竞争优势.
3.2 浮游藻属会阻碍光强入射,共存的竞争藻属不仅会自遮蔽还会互相遮蔽.考虑浮游藻属的动态自遮蔽作用,不会改变最终的竞争优势藻属.但是在紊动较弱的水体中,会加速微囊藻属取得竞争优势;在紊动剧烈的水体中,会限制小球藻属的无限制生长.
