二氧化碳排放与经济增长关系的实证分析
2018-07-26陈建成白羽萍王国峰北京林业大学经济管理学院北京0083中国科学院地理科学与资源研究所北京000中国科学院农业政策研究中心北京000中国科学院大学北京000山西财经大学国际经济与贸易学院山西太原03000山东师范大学地理与环境学院山东济南2038
赵 哲,陈建成*,白羽萍,王国峰,刘 雨 (.北京林业大学经济管理学院,北京 0083;2.中国科学院地理科学与资源研究所,北京 000;3.中国科学院农业政策研究中心,北京 000;4.中国科学院大学,北京 000;.山西财经大学国际经济与贸易学院,山西 太原 03000;.山东师范大学地理与环境学院,山东 济南 2038)
近年来,随着全球各国工业化进程加剧,伴随着大量能源消耗产生的温室气体尤其是二氧化碳,被认为是全球气候变暖的主要驱动因子[1-3].美国国家航空航天局(NASA)数据显示,1880年以来,全球平均气温上升了 0.8℃,照此趋势,本世纪内,全球地表温度将上升 2~6℃.全球升温带来的极端气象灾害在给世界各国带来巨大经济损失的同时也威胁着各国人民的生命安全.2009年哥本哈根大会使得“相较于工业革命前全球平均温度的增温幅度控制在2℃之内,相应的二氧化碳浓度不超过 450×10-6”成为各国间的政治共识;2015年在巴黎举办的联合国气候变化大会上,195个与会国家达成通过减少温室气体尤其是二氧化碳排放量来抑制全球升温的减排计划.但是,政府间气候变化委员会(IPCC)研究指出:工业革命以来,由于人类经济活动所产生的二氧化碳排放量占全球二氧化碳排放总量的 95%以上.那么减少二氧化碳排放是否会影响经济增长?若有,不同经济发展水平的国家或地区二者间相互影响程度是否相同?2014年,中国二氧化碳排放量达到100亿t,占全球二氧化碳排放总量的 30%,超过美国和欧洲排放量的总和,成为全球最大的碳排放国家1数据来源:《Global Carbon Project,2015》.在此背景下,探求“二氧化碳排放”与“经济增长”间的相互关系及影响程度具有重要的现实与学术意义,也为我国制定节能减排方案提供一定的参考依据.
现有关于碳排放与经济增长间关系的研究主要包括线性关系[4-5],N型曲线关系[6],以及倒 U型曲线关系[7-8],虽然大多数学者的研究支持倒 U型曲线关系即环境库兹涅茨曲线(EKC),但 Robalino-López等[9], Baek[10]的研究显示,倒U型曲线并不成立,学界对于碳排放与经济发展间关系尚未达成共识[11],且Coondoo and Dinda[12], Dinda[13]的研究指出,相比于“EKC假说”单方面探究经济增长对二氧化碳排放的影响,从“因果角度”讨论二者关系更为合理.此后越来越多的学者选择用“因果检验”的方式探求经济增长与二氧化碳排放之间相互作用的反馈机制.然而,在数据选择上,现有研究大多选取面板数据,且主要针对单一国家进行分析,例如Hamit-Haggar[11], Shahbaz等[14],Shahbaz等[15], Ozturk等[16], Xiong[17]的研究分别基于面板数据,分析加拿大,巴基斯坦,印度尼西亚,土耳其,中国经济增长与二氧化碳排放间的因果关系,研究结果却不尽相同.面板分析框架的前提是假定研究对象具备相同的发展轨迹,而时间序列能够更好的分析变量间的相互关系[17-18].基于此,本文在选取长时间序列的同时,根据区域发展特点,通过构建向量自回归(VAR)模型进行格兰杰因果检验,探求不同地区经济发展水平与人均二氧化碳排放量之间因果关系以及二者间相互影响.
1 样本选择及研究方法
1.1 样本选择
本文选取了北美地区(NA),欧洲地区(EU),东亚及太平洋地区(EAP),南亚地区(SA),中东及北非地区(MENA),拉美及加勒比海地区(LAC)6个区域的生产总值(现价美元价格)和人均二氧化碳排放量的指标值进行分析,进而探求经济增长与二氧化碳排放间的关系.之所以选择这 6个地区,主要是由于各区域内国家政治,经济联系密切,发展方式具有相对一致性,且各区域间经济发展水平具有显著差别,处在工业化的不同阶段.例如,北美、欧洲区域内各国经济发展水平明显高于其他区域国家,处于工业化后期;而南亚各国均属于发展中国家,整体发展水平不高,处于工业化初期.变量间的异质性有助于更好的探求其中的关系.样本区域及样本数据时期说明如表 1所示.数据均来自世界银行网站及欧洲统计局,各变量均为年度变量.
1.2 研究方法
1.2.1 平稳性检验 平稳性通常是时间序列分析的基础,而时间序列平稳性检验的方法众多.由于进行协整检验的前提条件是被检测的变量必须是同根的时间序列.因此,本文选用单位根方法对时间序列的平稳性进行检验.单位根检验以DF检验和ADF检验最为常见,而ADF检验是DF检验的拓展,即ADF检验是DF检验从AR(1)到AR(P)的拓展.其模型为:

将AR(P)模型写成以下形式用于单位根的检验:

1.2.2 协整检验 协整理论主要强调:通过将两个或两个以上非平稳变量进行线性组合,从而抵消趋势项的影响,使组合后的变量成为平稳变量,进而探求非平稳经济变量间蕴含的长期均衡关系,避免了用差分后的序列进行建模时产生的长期调整信息丢失的问题.协整检验的常见方法有 E-G两步检验与约翰森检验法,约翰森检验法主要检验多变量间的协整关系,而对于两变量间的协整关系,则通常选择 E-G两步检验法[20-21].首先构建协整回归方程并计算非均衡误差:
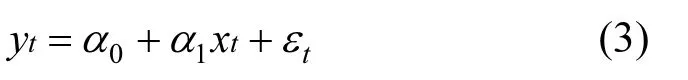
接下来,对残差进行单位根检验,若 α=0,意味着误差项et是平稳序列,说明变量间存在长期协整关系,否则就不存在协整关系:
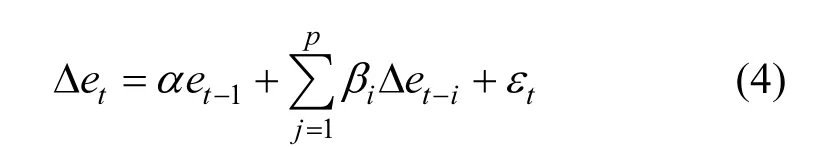
1.2.3 VAR模型检验 VAR模型实质上是考察多个变量之间的动态互动关系,把系统中每一个内生变量作为所有变量滞后项的函数来构造回归模型,一般形式如下:

式中:Y表示K维的内生变量向量; A表示相应的系数矩阵; P表示内生变量滞后的阶数.建立VAR模型时,滞后阶数的确定是一个关键的步骤,一般根据 LR、FPE、AIC、SC和HQ等信息准则来确定.
1.2.4 脉冲响应函数检验 Granger因果检验只能说明变量间的因果关系,而对于具体的影响过程以及影响方向则需要借助于脉冲响应函数进行分析.脉冲响应函数是一个变量作用对另一个变量的动态特征,因此可以通过考察系统的脉冲函数对分析结果进行补充和验证.
1.2.5 格兰杰因果检验 在通过协整检验确定变量间是否具备长期稳定关系后,若想判断变量间的因果关系,需要进行 Granger因果关系检验来判断变量间的因果性.格兰杰检验的基本思想是:检验当期Y值在多大程度上可以被前期Y值解释,如果在回归模型中添加X的滞后项后,有助于预测Y值,提高模型的解释能力,则认为X是Y的格兰杰原因.
2 结果分析
2.1 单位根检验
区域经济发展与人均二氧化碳排放量的ADF检验结果如表2所示.
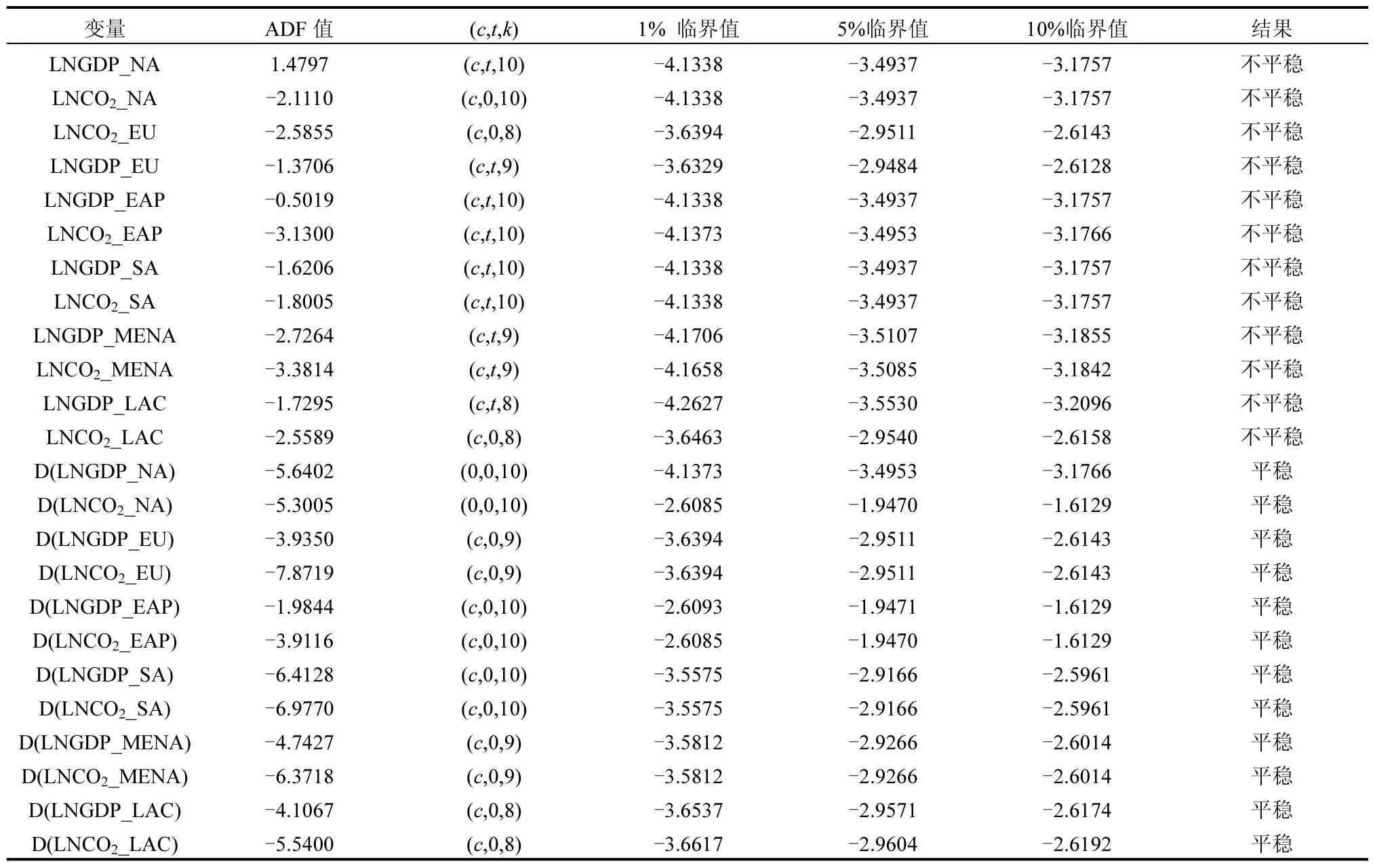
表2 ADF检验结果Table 2 The results of ADF test
由表 2可知,在 5%的显著水平下,上述各时间序列变量原序列的ADF值的绝对值均小于5%临界值的绝对值,因此不能拒绝序列存在单位根的原假设,各个变量的原序列均存在单位根,是不平稳序列.而它们的一阶差分序列的ADF的绝对值均大于5%临界值的绝对值,因此我们拒绝各个变量一阶差分序列存在单位根的原假设,各个变量的一阶差分序列均不存在单位根,为平稳序列,即各变量为一阶单整序列I(1),可以进行协整分析.
2.2 协整检验
本文选取样本区域人均二氧化碳排放量作为被解释变量,生产总值作为解释变量,分别构建6个一元回归模型,其模型的表达式为:


式中: LNCO2_NA、LNCO2_EU、LNCO2_EAP、LNCO2_MENA和LNCO2_LAC分别表示北美、欧洲、东亚及太平洋、南亚、中东及北非和拉美及加勒比海地区的人均二氧化碳排放量; LNGDP_NA、LNGDP_EU、LNGDP_EAP、LNGDP_MENA 和LNGDP_LAC分别表示北美、欧洲、东亚及太平洋、南亚、中东及北非和拉美及加勒比海地区的生产总值;α0、γ0、β0、δ0、φ0和ϕ0为常数项,α1、γ1、β1、δ1、φ1和ϕ1为各地区经济发展程度对当地人均二氧化碳排放量的影响系数;et为随机误差项.
随后,采用普通最小二乘法 (OLS)对上述建立的模型进行回归分析,结果如表3所示.
由表3可以看出,各回归模型调整后的R2均大于0.9,说明各模型的拟合程度较好,即各个方程的自变量对因变量的解释程度较高,DW 值均接近于 2,表明各方程的残差项不存在自相关.从自变量的回归系数来看,生产总值的回归系数均通过了 1%水平下的显著性检验,其中,北美和欧洲地区生产总值的回归系数显著为负,表明随着北美地区经济的发展,人均二氧化碳排放量是减少的,东亚及太平洋、南亚、中东及北非、拉美及加勒比海地区生产总值的回归系数均显著为正,表明随着区域经济的发展,人均二氧化碳排放量是增加的;从影响系数的大小来看,南亚地区的回归系数最大,为 0.432,表明南亚地区经济发展对于能源消耗的依赖程度较高,实现碳减排目标必然要经历坎坷艰辛的过程.接下来对上述六个模型的残差序列进行单位根检验,检验结果如表4所示:
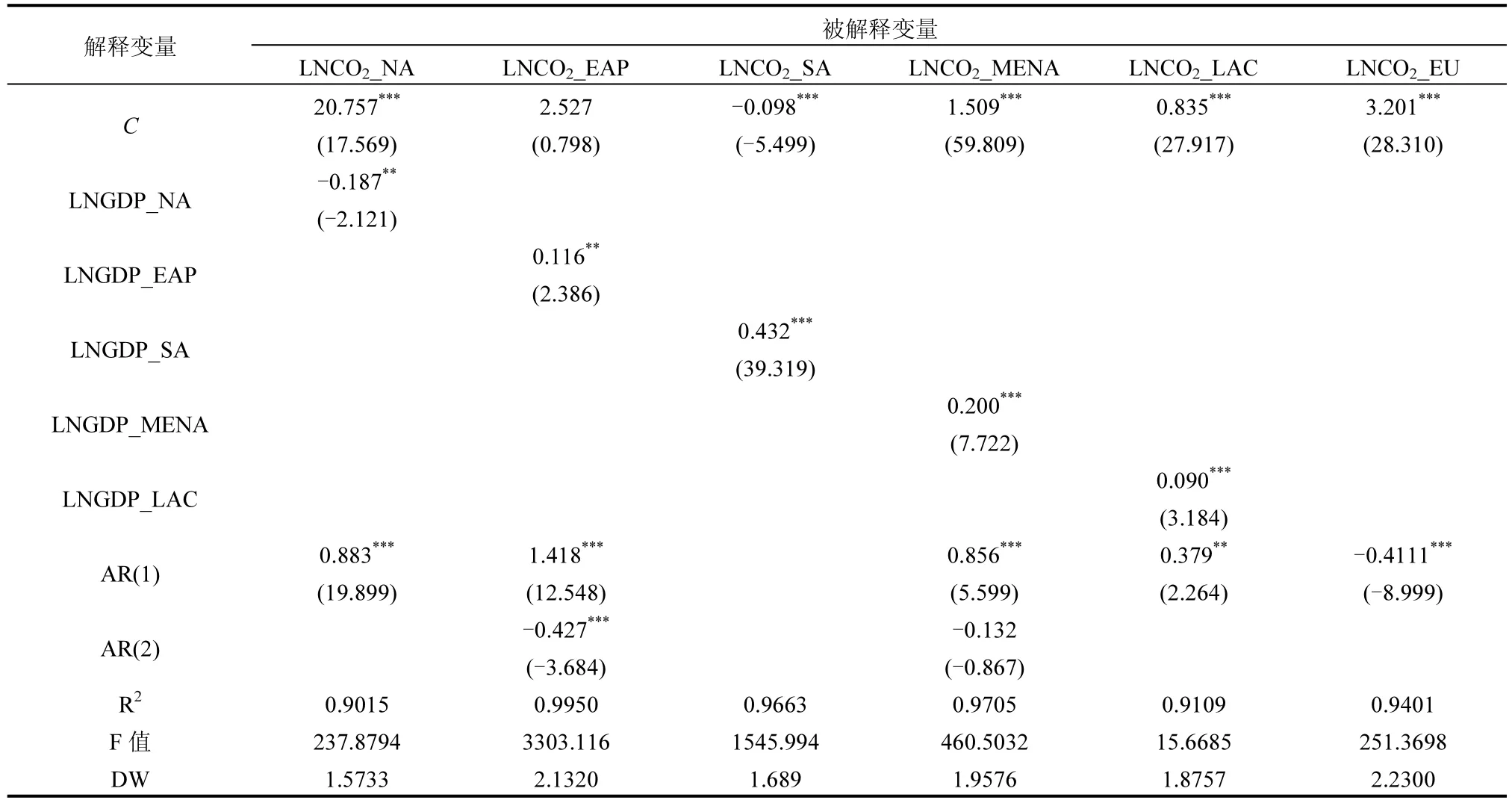
表3 回归结果Table 3 The results of regression

表4 残差序列平稳性检验结果Table 4 The stability test result of residual sequence
从表4可以看出,在 1%的显著性水平下,各区域 的回归残差均是平稳的,说明样本区域的生产总值与人均二氧化碳排放量之间存在长期均衡关系.
2.3 VAR检验
为了研究北美、东亚及太平洋、南亚、中东及北非和拉美及加勒比海地区生产总值与人均二氧化碳排放量之间的动态关系,本文构建 VAR模型进行分析.根据LR、FPE、AIC、SC和HQ等信息准则来确定最佳滞后阶数,鉴于在构建样本区域的生产总值与人均二氧化碳排放量的 VAR模型时,滞后阶数均为2.因此我们建立VAR(2)作为考察各个区域生产总值与CO2排放量关系的模型方程.构建方程如下:

式中:Ai为2×2阶系数矩阵.
检验上述 VAR(2)模型的稳定性,运用 Eviews7.0软件画出AR Roots Graph得到图1.
图1分别是北美、欧洲、东亚及太平洋、南亚、中东及北非和拉美及加勒比海地区的生产总值与人均二氧化碳排放量之间构建的 VAR(2)模型的稳定性检验结果,从中可以看出AR特征根倒数的模均都落在单位圆内,说明上述构建的VAR模型平稳.即短期内,当模型中的某个变量发生变化时,会使得模型中其他变量随之发生变化,但从长期来看,某个变量的变化对其他变量的影响会逐渐减弱,从整体来看,我们所选的各个区域生产总值与人均二氧化碳排放量之间所构成的系统是稳定、可靠的.可以进行脉冲响应函数分析.
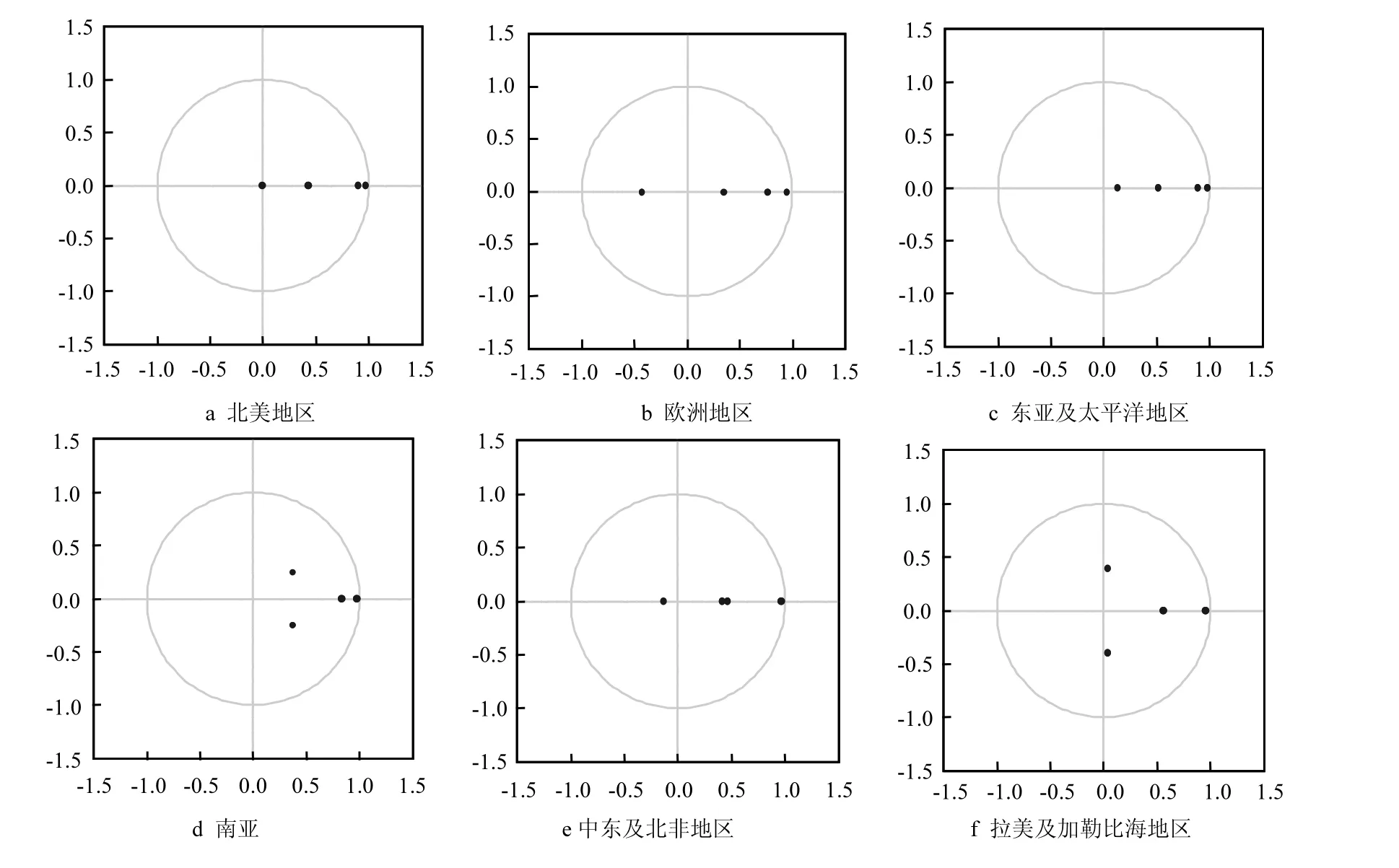
图1 VAR模型稳定性检验Fig.1 Stability test of VAR model
2.4 脉冲响应函数
在样本区域生产总值与人均二氧化碳排放量的VAR(2)模型基础上,本文通过脉冲响应函数分析变量间相互的动态关系,结果如图 2所示.其中,纵轴表示选取经济指标的响应程度,实线代表脉冲响应函数,虚线则表示正负两倍标准差偏离带;横轴表示冲击作用的滞后期长度,本文选取滞后 10期来观测变量之间的影响程度.
由图 2可以看出,北美地区经济发展对人均二氧化碳排放量的冲击效果,从第 1期开始保持逐渐增强的负向冲击作用,在第 4期这种负向冲击效果达到最大,随后逐渐减弱.表明随着北美地区经济的发展,人均二氧化碳排放量会逐渐减少;图 3可以看出北美地区人均二氧化碳排放量对经济发展的冲击效果,从第 1期开始始终为较强的正向冲击效果,表明北美地区人均二氧化碳排放量的增加可以促进北美经济的发展.
由图4可以看出,欧洲地区经济发展对人均二氧化碳排放量的冲击效果,从第1期开始保持逐渐增强的正向冲击作用,在第2期这种正向冲击达到最大,随后逐渐减弱,在第6期后转为负向冲击,且负向冲击不断增加;表明欧洲地区经济的发展会使该地区人均二氧化碳排放量呈现先增加后减少的变化趋势;图5可以看出欧洲地区人均二氧化碳排放量对该区域经济发展的冲击效果,从第1期开始保持逐渐减弱的正向冲击效果,在第 5期转为负向的冲击,并逐渐增强;表明欧洲地区人均二氧化碳排放量增加对区域经济发展呈现前期促进,后期抑制的影响效果.

图2 北美地区人均CO2排放量对GDP的脉冲响应Fig.2 The impulse response of CO2 per capita to GDP in North America
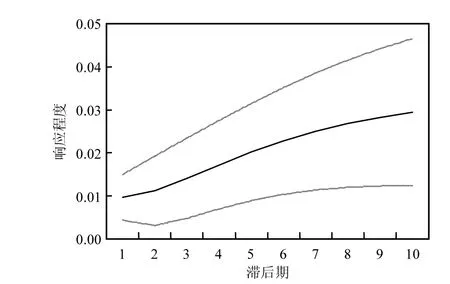
图3 北美地区GDP对人均CO2的脉冲响应Fig.3 The impulse response of GDP to CO2 per capita in North America
从北美与欧洲地区脉冲响应结果可以看出,两地区均已跨过碳排放峰值拐点,符合 EKC假说“当经济发展达到一定水平后,随着人均收入的进一步增加,二氧化碳排放量由高趋低,环境污染程度逐渐减缓”的阐述.区域经济发展对于能源消耗的依赖程度降低,有利于实现区域可持续发展.
由图6可以看出,东亚及太平洋地区经济发展对人均二氧化碳排放量的冲击效果,脉冲结果与北美、欧洲地区明显不同,从第1期开始保持逐渐增强的正向冲击作效果,表明东亚及太平洋地区的经济发展会导致人均二氧化碳排放量的增加;图7可以看出东亚及太平洋地区人均二氧化碳排放量对经济发展的冲击效果,从第 1期开始为较强的正向冲击效果至第 7期开始保持稳定;表明东亚及太平洋地区人均二氧化碳排放量的增加会推动该区域经济的发展.
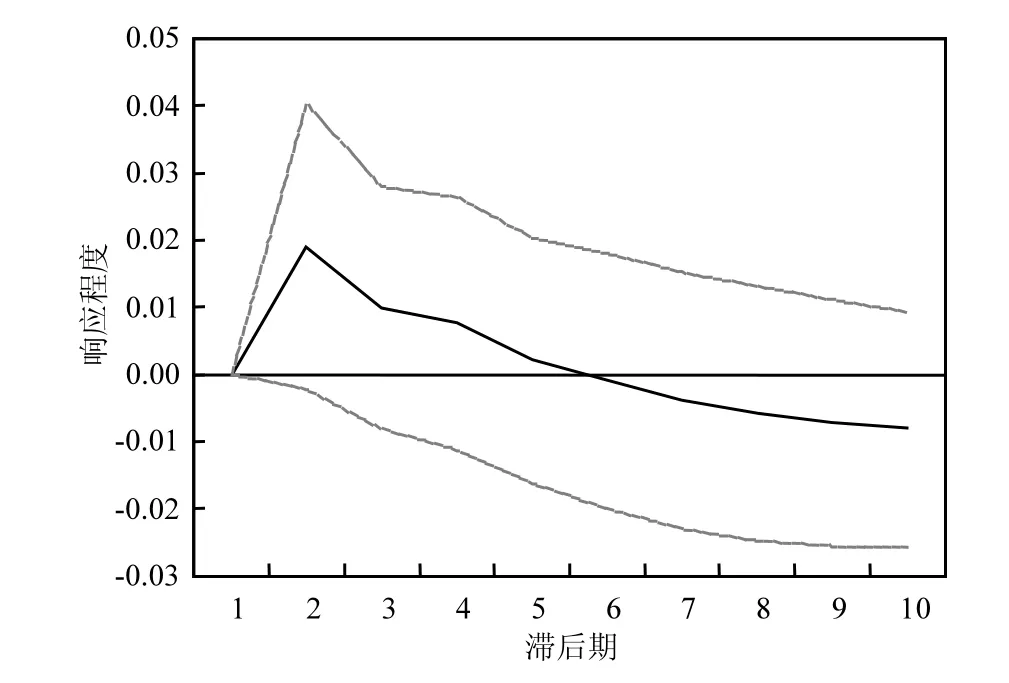
图4 欧洲地区人均CO2排放量对GDP的脉冲响应Fig.4 The impulse response of CO2 per capita to GDP in Europe
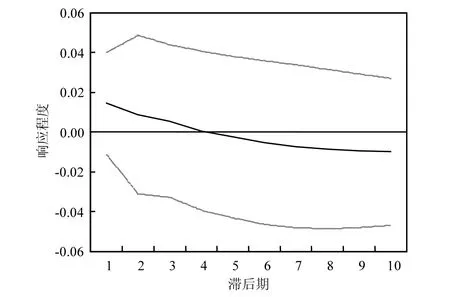
图5 欧洲地区GDP对人均CO2排放量的脉冲响应Fig.5 The impulse response of GDP to CO2 per capita in Europe
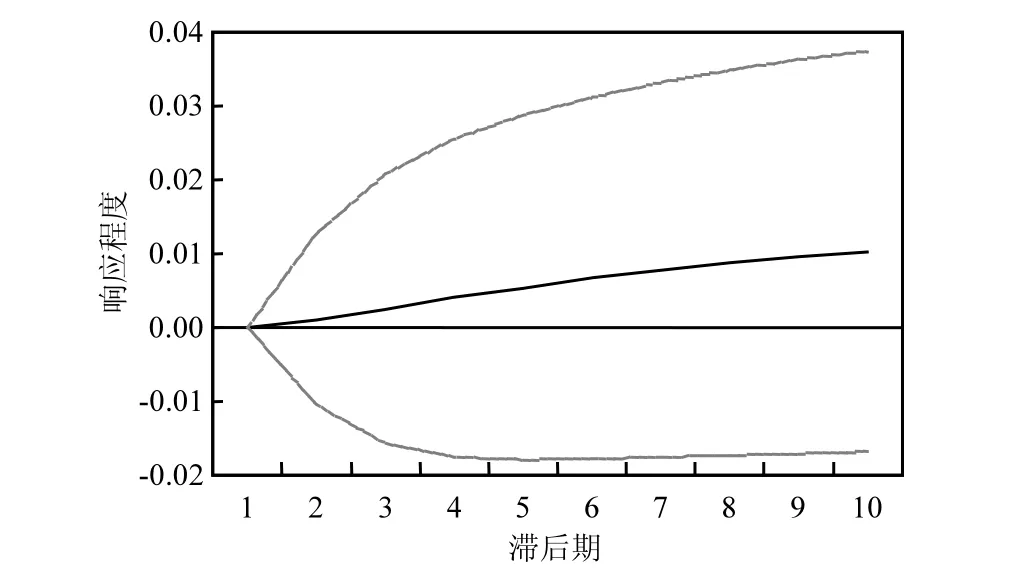
图6 东亚地区人均CO2排放量对GDP的脉冲响应Fig.6 The impulse response of CO2 per capita to GDP in East Asia and the Pacific
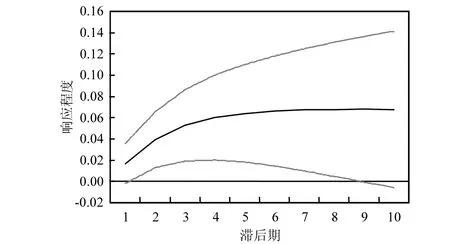
图7 东亚地区GDP对人均CO2排放量的脉冲响应Fig.7 The impulse response of GDP to CO2 per capita in East Asia and the Pacific
由图8可以看出,南亚地区经济发展对人均二氧化碳排放量的冲击效果,从第1期开始保持逐渐增强的正向冲击效果,表明随着南亚地区经济的发展,该地区人均二氧化碳排放量是增加的;图 9可以看出南亚地区人均二氧化碳排放量对该区域经济发展的冲击效果,从第一期开始为较强的负向冲击效果,在第2期这种负向冲击达到最大,之后这种负向冲击逐渐减弱,在第 5期转为逐渐增强的正向冲击;表明南亚地区人均二氧化碳排放量的增加在短期内会抑制该区域经济的发展,但从长期来看依然会促进该区域经济的发展.
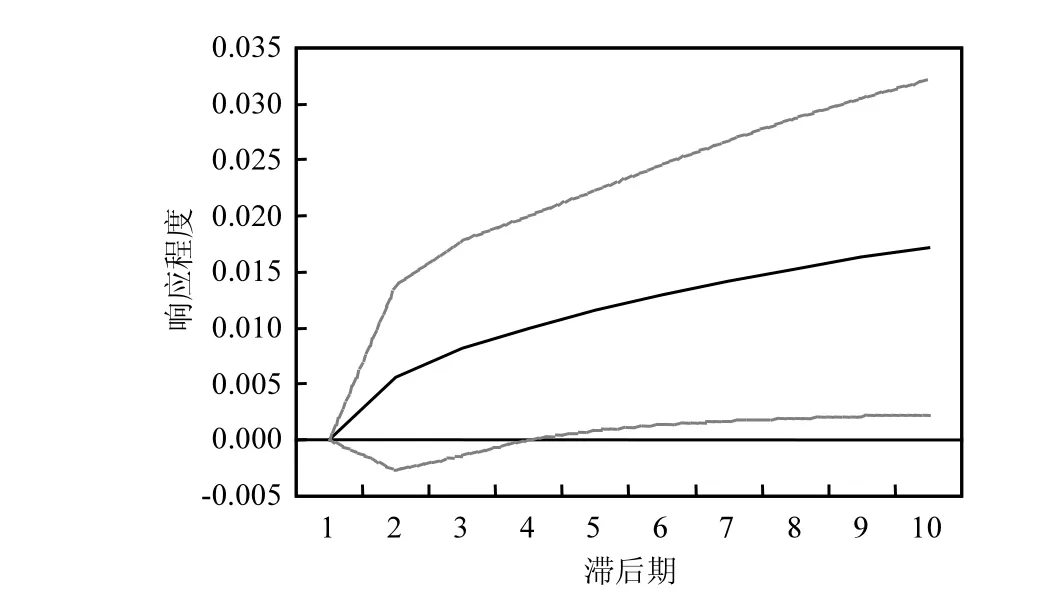
图8 南亚地区人均CO2排放量对GDP的脉冲响应Fig.8 The impulse response of CO2 per capita to GDP in South Asia
从东亚与南亚地区脉冲响应结果可以看出,两地区经济发展均会产生大量的二氧化碳排放,这主要由于该区域内国家大多处于工业化初期,经济增长对于能源消耗依赖程度较高,且发展方式粗放,随着工业化与城市化进程加剧,该地区对于能源的刚性需求会愈发强烈,减少二氧化碳排放必然会付出沉重的社会经济代价.因此,实现减碳目标要在优化产业结构的同时,加大技术研发投入力度,通过工业技术创新提升产业环境绩效,使用清洁能源,发展低碳型经济,从而降低二氧化碳减排带来的社会经济损失.

图9 南亚地区GDP对人均CO2排放量的脉冲响应Fig.9 The impulse response of GDP to CO2 per capita in South Asia
此外,作为全球最大的二氧化碳排放国家,中国的碳减排工作对全球二氧化碳减排目标的实现有着重大影响.国家政策制定应专注于工业能源消费总量管理,在优化能源结构和产业结构,淘汰落后生产能力,减少产能过剩的同时加快发展绿色产业,从而降低能耗和环境污染.同时,完善碳税与碳交易市场,运用市场方式优化各种减排资源的配置,提高减排效率与实现减排的持续性.
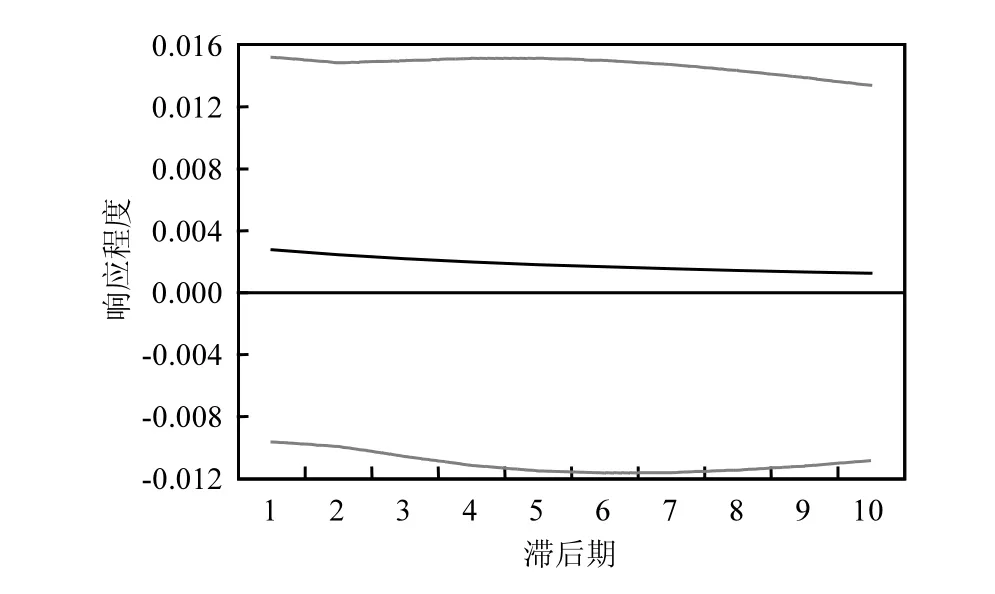
图10 中东及北非地区人均CO2排放量对GDP的脉冲响应Fig.10 The impulse response of CO2 per capita to GDP in Middle East and North Africa
由图 10可以看出,中东及北非地区经济发展对该区域人均二氧化碳排放量的冲击效果,从第1期开始保持逐渐减弱的正向冲击效果,表明中东及北非地区经济发展会增加该区域人均二氧化碳的排放,但是这种影响程度非常微弱.这或许是由于该区域国家经济增长大多依赖于能源与原材料出口而非制造业和工业化,例如沙特阿拉伯、摩洛哥、伊朗等国家;图11可以看出中东及北非地区人均二氧化碳排放量对该区域经济发展的冲击效果,从第1期开始保持较强的正向冲击效果,在第6期这种正向冲击达到最大,随后逐渐减弱;表明中东及北非地区人均二氧化碳排放量的增加会促进该区域经济的发展.
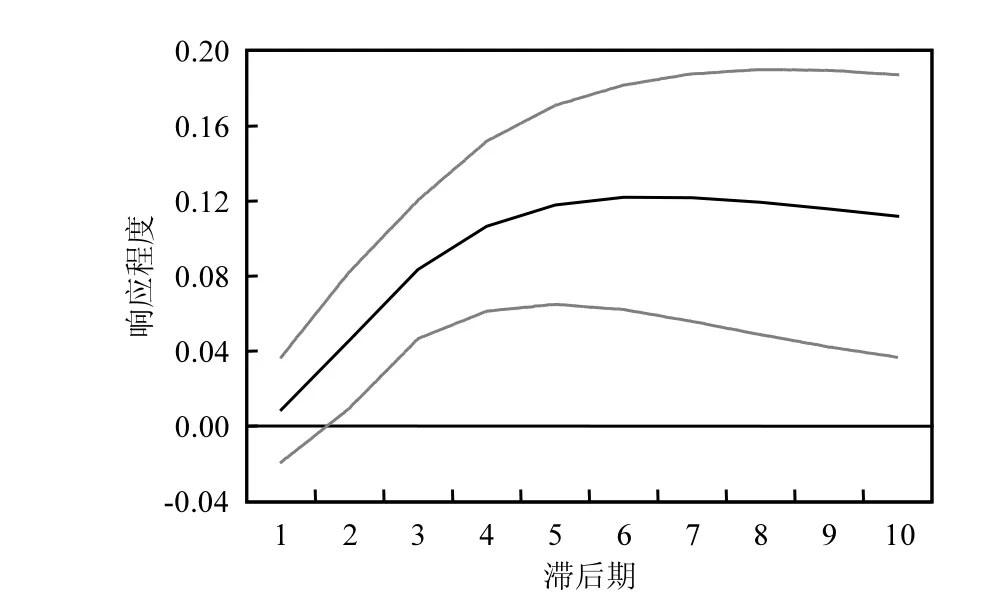
图11 中东及北非地区GDP对人均CO2排放量的脉冲响应Fig.11 The impulse response of GDP to CO2 per capita in Middle East and North Africa

图12 拉美及加勒比海地区人均CO2排放量对GDP的脉冲响应Fig.12 The impulse response of CO2 per capita to GDP in Latin America and the Caribbean
由图 12可以看出,拉美及加勒比海地区经济发展对该区域人均二氧化碳排放量的冲击效果,从第 1期开始保持逐渐增强的正向冲击作用,在第2期这种正向冲击达到最大,随后逐渐减弱,第9期开始基本保持稳定;表明拉美及加勒比海地区经济的发展会使人均二氧化碳排放量增加;图 13可以看出拉美及加勒比海地区人均二氧化碳排放量对该区域经济发展的冲击效果,从第1期开始保持逐渐增强的正向冲击效果,在第 5期这种正向冲击达到最大,随后逐渐减弱;表明拉美及加勒比海地区人均二氧化碳排放量增加会促进改区域经济的发展.

图13 拉美及加勒比海地区GDP对人均CO2排放量的脉冲响应Fig.13 The impulse response of GDP to CO2 per capita in Latin America and the Caribbean
2.5 格兰杰因果检验
对于区域经济发展与人均二氧化碳排放量间的因果性检验,结果如表5所示.
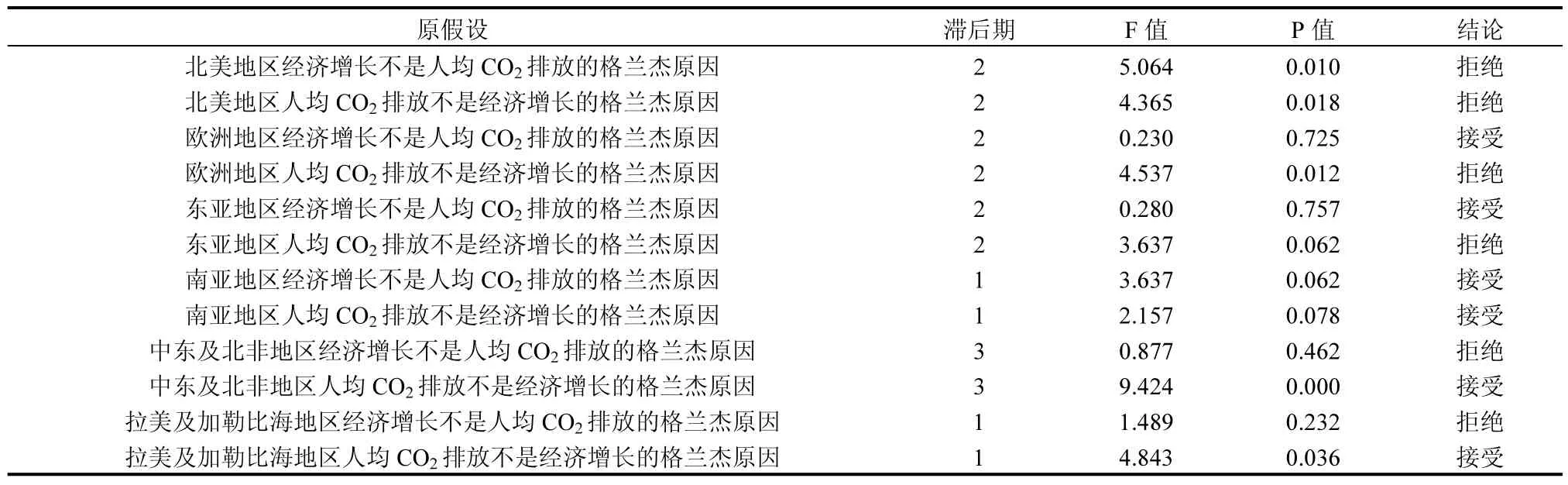
表5 格兰杰因果检验结果Table 5 The results of Granger causality test
由表 5可以看出,在 5%的置信水平下,北美地区经济发展与人均二氧化碳排放量互为格兰杰原因,表明北美地区经济发展会引起人均二氧化碳排放量的变化,而人均二氧化碳排放量的变化也会引起该区域生产总值的变化;在 10%的置信水平下,欧洲地区和东亚及太平洋地区人均二氧化碳排放量是经济增长的格兰杰原因,而经济增长不是人均二氧化碳排放量的格兰杰原因;同样在 10%的置信水平下,南亚地区的结果与北美地区结果相同,在1%与5%的置信水平下,中东及北非地区与拉美及加勒比海地区的结果则与东亚地区相同,即该区域经济增长是人均二氧化碳排放的格兰杰原因,而人均二氧化碳排放并非该区域经济增长的格兰杰原因.
3 结语
根据协整及残差序列平稳性检验结果,各区域经济发展与人均二氧化碳排放量存在长期均衡关系,从回归系数可以看出经济发展对二氧化碳排放的影响程度,其中,南亚地区回归系数最大,表示该区域经济增长对于能源消耗的依赖程度最高;此外,现有研究大多基于 EKC假说单方面探求经济增长对二氧化碳排放量的影响,本文通过格兰杰因果检验探求二者间因果关系及相互影响,结果显示,各区域经济发展均会对本地区人均二氧化碳排放量产生影响,但人均二氧化碳排放量并非都是该区域经济发展的格兰杰原因,也就是说经济增长是二氧化碳排放量增加的一个刺激因素,而二氧化碳排放并不一定是经济增长的刺激因素;从脉冲响应函数的结果可以看出,在区域经济发展对人均二氧化碳排放量的影响上,除北美与欧洲地区外,其他地区经济发展都会带来人均二氧化碳排放量的增加,但影响程度存在差异.主流研究 EKC假说认为“二氧化碳排放量在低收入水平上随人均GDP增加而上升,高收入水平上随 GDP增长而下降”,这在本文研究区域中的北美、欧洲、东亚、南亚、拉美地区都是成立的,尤其是欧洲地区,基本符合倒U型曲线的变化趋势,一定程度上验证了EKC假说.但是从中东及北非地区的脉冲响应结果我们看出,虽然该区域不乏沙特、阿联酋等人均GDP较高的国家,但经济增长对二氧化碳排放存在正向影响,影响程度比较微弱,其原因可能在于区域内国家经济发展主要依靠能源出口、工业基础薄弱等原因.基于此,本文认为二氧化碳排放量变化不仅取决于经济发展水平,也受到经济发展方式和资源禀赋的影响,随着经济增长达到某个拐点时,二氧化碳排放量达到峰值,随后逐渐减少一定程度上是通过清洁能源使用、产业机构优化、生产工艺提高而实现的.因此,在全球减碳过程中,应该根据不同区域或国家的经济发展水平制定减排目标,寻求经济发展与二氧化碳减排的均衡区间,以最小的社会经济代价达到全球二氧化碳减排目标.
