岩质边坡倾倒变形机理及稳定性研究综述

安晓凡，李 宁，孙闻博

(西安理工大学岩土工程研究所，陕西 西安 710048)

0 引言

伴随着众多水利水电、露天矿、交通工程等大型项目的建设，岩质边坡倾倒失稳的现象被逐渐发现和揭露，成为制约此类工程建设的重点和难点问题，逐步引起国内外学者、工程师的广泛关注。

倾倒变形是边坡岩体向临空面倾覆的一种失稳模式，多发生于反倾层状的岩质边坡中。早期普遍认为反倾边坡的自稳能力好于顺层边坡，变形常发生于浅层岩体中，不会出现大规模由于岩层倾倒变形触发的滑动失稳现象。但是我国是一个地质灾害频发的国家，近30年来，西南、西北等高山峡谷地区不断揭露出弯曲倾倒变形深度高达上百米的边坡，这种变形模式很可能会发展为大型和巨型的深层滑坡[1]。因此，对易发生倾倒变形的岩质边坡进行失稳机理、稳定性分析与评价方法以及治理措施的研究至关重要，具有理论意义和实际应用价值。

Müller[2]在对意大利Vaiont拱坝上游左岸滑坡的研究中首次提出了自然岩块的倾覆(Overturning)现象。基于理论和试验模型，Ashby[3]对此失稳现象提出了简单的评价准则，并且用倾倒(Toppling)来描述此类现象。金川露天矿边坡是我国最早发现，也是报道最为详细的边坡倾倒破坏实例之一[4-5]。1974年下半年，一矿区边坡受开挖、连续降雨和坡底大规模爆破的影响，岩体向矿坑方向倾倒变形，岩层倾斜10°左右，最大水平位移高达7 m。该矿区东部采场边坡于1990年2月出现变形破坏的急剧加速，边坡前缘观测点水平位移速度由每天几十毫米增至200 mm左右, 最高达358 mm/d，垂直位移量最高达331 mm/d。下盘边坡形成数条长达数十米至数百米，相对上升4～10 m的反翘陡坎；3月24日，上盘边坡大面积坍塌，近3.0×105m3的岩石滑移堆于坑底。此后，我国的龙滩水电站坝址左岸边坡、红莲池铁矿边坡、盐池河磷矿边坡、重庆武隆鸡尾山、锦屏一级水电站左岸边坡、茨哈峡水电站I号倾倒体、三峡库区巫峡段龚家坊2#斜坡、溪洛渡水库星光三组倾倒变形体、昌马水库枢纽工程边坡、天生桥二级水电站厂房南侧边坡等均出现不同程度的倾倒变形，轻则致使坡表出现裂缝、掉块现象，重则导致大规模山体崩塌、滑动破坏。

本文在阐述岩质边坡倾倒变形机理的基础上，结合国内外研究成果，详细总结了倾倒边坡的稳定性分析与评价方法，提出了基于力矩平衡的弯曲倾倒解析方法，并且对所存在的问题和下一步的研究方向进行了探讨。

1 岩质边坡倾倒变形的特点和类型

1.1 倾倒变形的分类

Goodman等[6]将岩质边坡的倾倒变形分为块体倾倒(Block toppling)、弯曲倾倒(Flexual toppling)、块体—弯曲倾倒(Block-flexual toppling)和次生倾倒(Secondary toppling)(图1、图2)。这种分类方式沿用至今，基本上涵盖了自然界能够观察到的倾倒边坡。

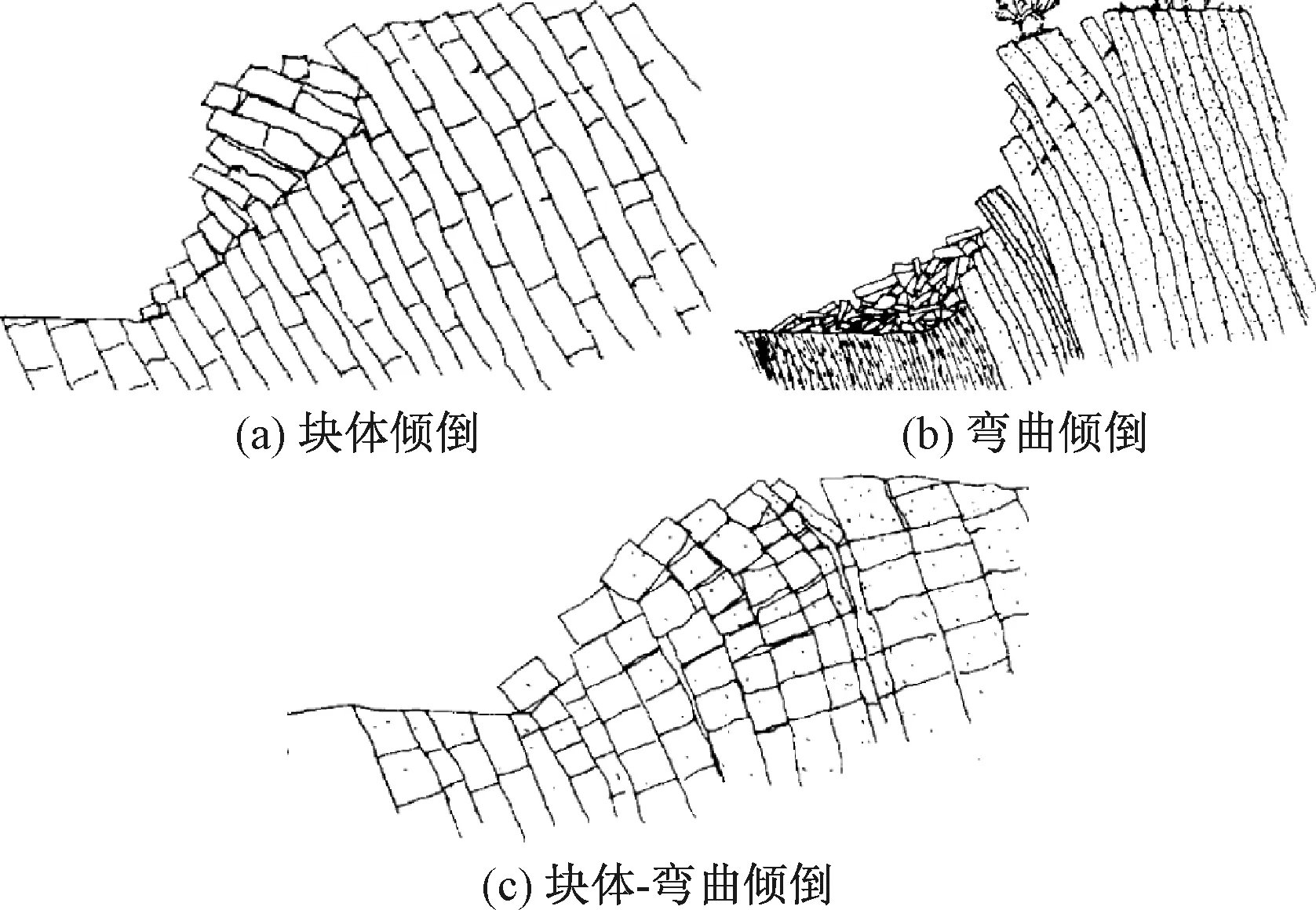
图1 边坡倾倒变形基本类型Fig.1 Basic types of toppling deformation

图2 次生倾倒类型Fig.2 Types of secondary toppling

坚硬岩柱被规模较大正交节理切割时可能会发生块体倾倒。构成边坡坡脚的短岩柱，由于受到后方翻倒下来岩柱的荷载作用而被向前推出，导致坡脚滑移。块体倾倒存在比较清晰的底面，通常是由一个个逐渐向上的阶梯状的横切节理组成(图1a)。弯曲倾倒多发生于非常发育的陡倾斜不连续面所分割的连续岩柱，由于悬臂岩柱向临空面运动导致层间滑移，因此会形成一系列逆向陡坎(图1b)。当岩柱被许多横节理切割，岩柱变形由横节理分割的各小岩块位移累计而成，形成似连续性弯曲状，则为块体—弯曲倾倒(图1c)。

次生倾倒也称作二次倾倒，按照倾倒岩体变形的触发形式不同，可以分为：底部滑移牵引上部岩体的倾倒(图2a)，上部变形体滑移推动下部岩体的倾倒(图2b)，上部岩体滑移促使坡角倾倒(图2c)以及陡倾岩体的拉伸倾倒破坏(图2d)。

实际边坡的倾倒变形往往是同时包含上述几种变形破坏模式的复合倾倒，变形破坏机理也更加复杂、很难预测。

现阶段倾倒边坡的理论研究和解析模型的建立基本上是以上述分类为基础。相对而言，对块体倾倒所开展的研究最多，分析理论也较为成熟；而弯曲倾倒的研究成果有限。对于复合倾倒和二次倾倒的理论研究也只是在近几年才有报道，大多停留在野外观测和统计分析方面。

1.2 倾倒变形的特点

倾倒变形的发生除了由于岩性和岩体结构的特殊组合形式外；长时间降雨入渗，库区水位变化，岩体冻融循环，人工开挖、爆破，洞室开挖、采矿活动等外界因素都可能会触发大规模的倾倒失稳。黄润秋[7]在分析我国典型滑坡灾害实例的基础上，对大中型反倾层状岩质边坡变形破坏规律得出以下认识：

(1) 反倾层状岩质边坡的大规模倾倒变形破坏与边坡的岩性软弱程度、岩层厚度等有密切关系。一般发生在具有“柔性”特点的反倾向或近直立薄层状地层中，尤其是以薄层状板岩、片岩、砂板岩互层、薄层状大理岩、泥质灰岩等岩性组合形式为主。

(2) 大规模的倾倒破坏存在一个很长的孕育演化过程。在此过程中，岩层可能发生很大的柔性弯曲而不折断，而其破坏一定是变形发展到极致的产物。不同于顺层边坡的潜在滑动面受一些先决条件控制，这类边坡滑动面的形成完全是自身演化的结果。然而一旦演化到滑坡阶段，由于其长期的地质历史积累，必然是深层的、大规模的。

(3) 陡倾的坚硬中—厚层状边坡岩体也常见倾倒破坏，但通常情况下，其变形和破坏的深度均不大，一般为30～40 m。与柔性地层时效变形的特点不同，这类地层通常发生的是“结构性质”的变形，即通过节理裂隙的“弯折”而表现出倾倒的特征。从人类工程活动的角度上，前者在其变形阶段的稳定性状态相对较好。后者的岩层变形可在较短时间内发生，稳定性也表现出较强的突发性特点。

2 倾倒边坡的稳定性分析方法

2.1 解析方法

2.1.1块体倾倒

Goodman等于1976年建立了岩质边坡块体倾倒稳定分析的计算模型，给出了对应的极限平衡分析方法(以下简称G-B方法)，该方法奠定了岩质边坡倾倒破坏分析的理论基础(图3)。1981年，Hoek等[8]在《Rock slope engineering》一书中直接引用了该论文的内容与结论，使得G-B方法得到广泛传播和应用。但是G-B方法所针对的只是块体倾倒这种模式，对于其他变形模式的计算模型和解析方法并未涉及。

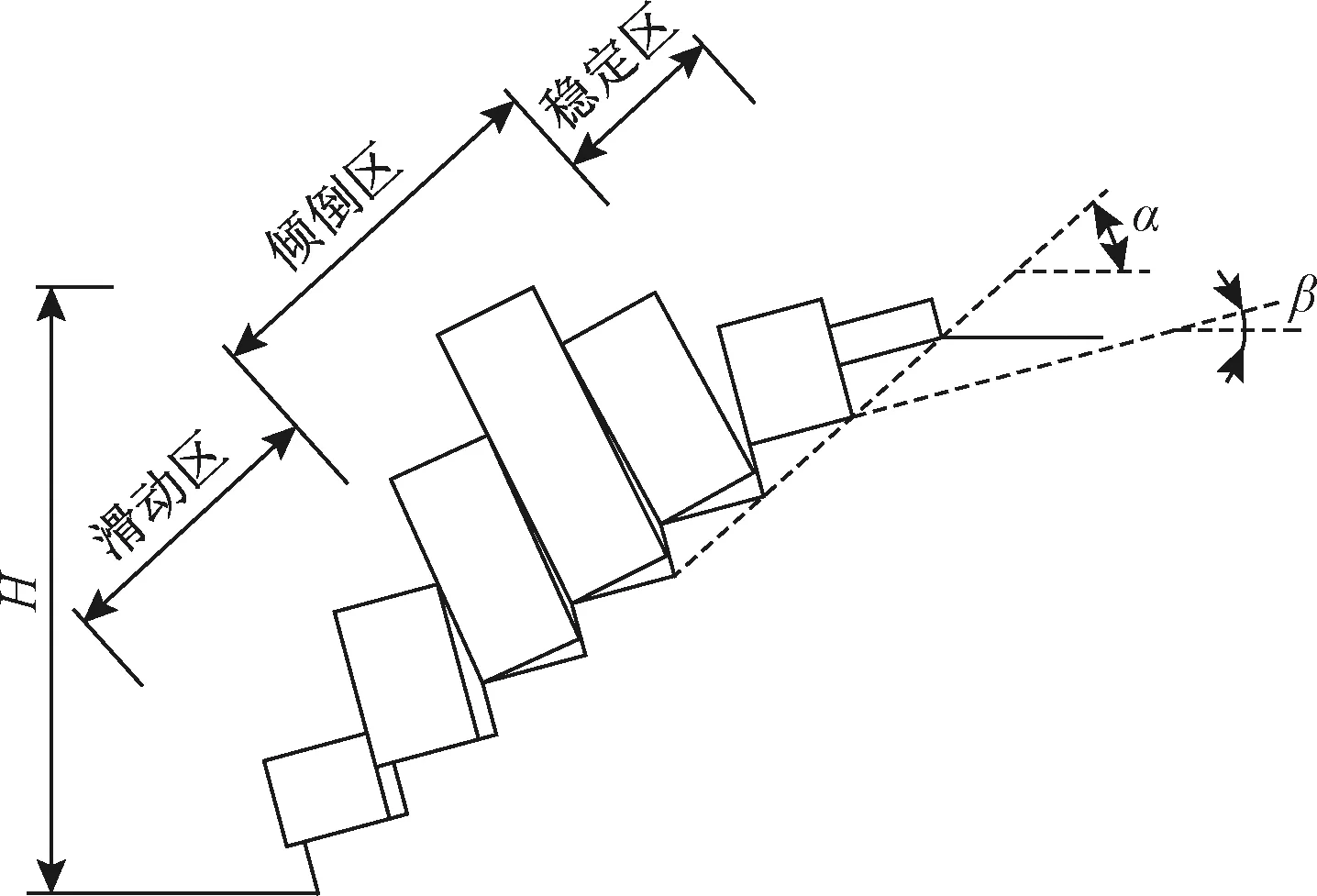
图3 块体倾倒计算模型Fig.3 Calculation model of block toppling

此后一些学者在Goodman等人研究的基础上做了一些论证和改进工作，使其适用性得以加强。Wyllie[9]首次将G-B方法应用在三个工程实例中，证实了该方法的适用性。Zanbak[10]通过程序实现G-B方法，并提出了图表法设计倾倒边坡的思路。Aydan等[11]基于极限平衡的概念，建立了块体倾倒的动态平衡方程，并通过试验验证其可行性。Sagaseta等[12]假定组成边坡的岩块厚度相对于其高度为一微量，采用微分方程来描述边坡中块体的平衡状态。但是该方法只有在岩柱的长细比大于一定值时才能保证计算结果的准确性。Liu等[13]基于极限平衡理论，提出了岩质边坡倾倒破坏分析的传递系数法。Babiker等[14]认为由于节理存在不符合实际的剪胀现象，导致极限分析过高估计了它的稳定性。进而提出的改进的塑形极限分析程序，考虑了非关联、低剪胀、摩擦模型。

国内学者也做了一些研究工作。孙广忠[15]建立了岩体结构转动和倾倒变形的力学模型，基于力矩平衡得出了结构体转动破坏和倾倒变形的计算公式和破坏判据。这与国外学者的研究思路不谋而合，岩体转动其实是块体倾倒的力学模型，而岩体倾倒变形的模型基础便是悬臂梁模型。但是该研究只是针对于单个块体而言，并没有给出整个边坡的系统解法。陈祖煜等[16]对G-B方法做出四点改进，即考虑岩柱底滑面的连通率、重新定义安全系数、确定破坏模式、将条块视为更一般的平行四边形，并给出相应的解析方法。之后在其著作中[17]详细介绍了改进的G-B方法，并且基于该方法编制了倾倒边坡的计算程序EMU。李天扶[18]指出G-B模型最大的缺陷是没有考虑水压力的作用，因此无法解释倾倒体的各种不规则现象，例如陡倾角的顺层边坡发生向外倾倒的现象等。在层状岩质边坡倾倒稳定分析中，应计入上层滞水产生的倾倒力矩，有效地排水应是对易发生倾倒的边坡首选的治理措施。刘才华等[19]、郑允等[20]分别基于传递系数法和连续性分析法的概念，提出了考虑地震作用的块体倾倒分析方法。郑允等[21]基于传递系数法，在G-B模型的基础上，提出了坡顶荷载作用下岩质边坡倾倒破坏地质力学模型和解析方法。高连通等[22]基于陈祖煜改进的G-B方法，推导了考虑地下水作用的反倾岩质边坡稳定性计算方法。

2.1.2弯曲倾倒

弯曲倾倒一般没有已知的破坏面，岩层在自重或外力的作用下向临空面发生弯曲变形，表现出明显的柔性特征。日本学者Aydan等[23]基于极限平衡方法，运用悬臂梁弯曲理论对G-B模型进行改进，建立了弯曲倾倒的力学模型，通过迭代求解得到反倾边坡坡脚剩余下滑力，该方法仍然以剩余下滑力作为边坡稳定性的判别标准，并通过室内基底摩擦试验进行了验证。该研究首次建立了弯曲倾倒的解析方法。计算模型见图4。

图4 弯曲倾倒计算模型Fig.4 Calculation model of flexual toppling

Adhikary等[24]通过离心机试验发现，倾倒折断面与岩柱并不是垂直的(G-B模型假定折断面与岩柱垂直)。并对Aydan等[23]提出的弯曲倾倒模型进行改进，得出了倾倒折断深度的计算公式以及安全系数的计算方法。之后Adhikary等[25]基于Cosserat理论建立了弯曲倾倒分析的模型，但是Cosserat模型无法考虑岩层间的滑移、错动。蒋良潍等[26]基于悬臂梁模型，并考虑板上下侧缘的层间错动阻力，统一地利用能量方法，推导了屈曲失稳和弯折破坏的判据。卢海峰等[27]在Adhikary提出的悬臂梁弯曲极限平衡分析模型的基础上，对其折裂面形式、层间凝聚力的影响和各层岩体重度等方面问题进行了修正。陈从新等[28]通过对模型试验的分析，将弯曲倾倒破坏区域分为滑移倾倒区和悬臂倾倒区，并且建立了相应的力学模型和分析方法。

2.1.3块体—弯曲倾倒和次生倾倒

实际工程中发生的边坡倾倒变形现象多是较为复杂的组合倾倒模式或二次倾倒变形。Evans[29]针对次生倾倒模式提出了应力重分布的分析方法。王思敬[4]介绍了金川露天矿边坡的滑动—倾倒复合变形实例，指出其变形是在两种机制共同作用下发生的，岩体条块状碎裂结构对变形机制和发展过程起到控制作用。伊朗学者Amini等[30]首次建立了弯曲—块体倾倒的力学模型(图5)，得出了这种变形模式的解析方法，并通过编程实现应用在两个典型的反倾边坡实例中(图6)。Mohtarami等[31]介绍了一种特殊的次生倾倒理论分析模型，即上部土体圆弧滑动、下部岩体块体—弯曲倾倒，并给出相应的解析方法。杨保军等[32]基于传递系数法，提出了岩质边坡上部滑动—下部块体倾倒组合破坏的解析分析方法。

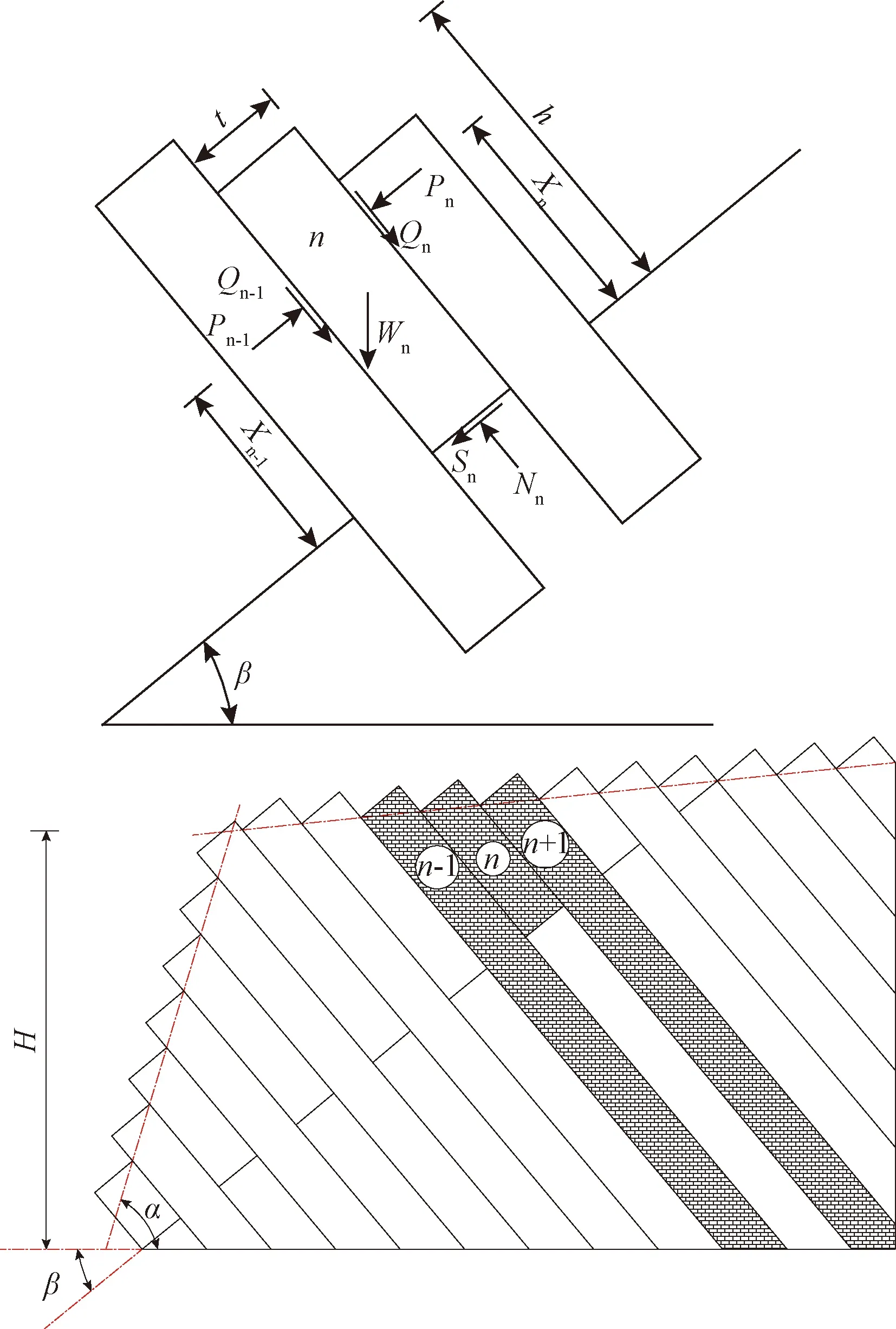
图5 块体—弯曲倾倒计算模型Fig.5 Calculation model of block-flexual toppling

图6 典型反倾边坡实例[30]Fig.6 Typical examples of anti-dipped slope

2.2 数值方法

随着计算机的广泛应用，研究人员不断尝试用各种数值方法来研究边坡的倾倒变形问题。其中最为常用的是离散元方法，代表软件是Itasca公司开发的UDEC和PFC，其次是石根华博士创立的非连续变形分析方法(DDA)，也有少数学者应用节理网格有限元和有限差分法展开研究。

离散单元法是Cundall[33]于1971年提出来的，该方法适用于研究在准静力或动力条件下节理系统或块体集合的力学问题。Ishida等[34]首次将离散元方法应用于裂隙岩体边坡块体倾倒变形的研究中。Pritchard等[35]最早利用离散元法分析大型边坡的弯曲倾倒破坏。程东幸等[36-37]利用三维离散元程序3DEC对反倾边坡的影响因素及反倾条件进行了模拟研究，并将其应用在对龙滩水电站工程边坡的三维变形特征分析中。Brideau等[38]通过两个不同约束条件的理想模型介绍了3DEC在分析块体倾倒边坡中的应用。蔡跃等[39]探讨了弯曲倾倒边坡的稳定性和岩层倾角、厚度及边坡倾角之间的关系。Alejano等[40]以西班牙一露天矿边坡为背景，介绍了一种新的次生倾倒破坏模式—上部倾倒、下部圆弧型滑动。在计算中首先用G-B方法求得上部倾倒体的下推力，然后将此力施加在下部滑体上，用离散元强度折减法对整体稳定性进行分析。王章琼等[41]研究露天矿边坡在自重、露采、地下开采等因素作用下的变形破坏特征。Li等[42]用基于连续模型的离散元方法(CDEM)模拟反倾露天矿边坡的弯曲倾倒变形。

颗粒离散元方法被应用在研究岩土体的破裂和裂纹的发展，以及颗粒间的相互作用问题、大变形问题、断裂问题等。一些学者用此方法来模拟边坡的倾倒变形。Scholtes等[43]介绍了颗粒离散元方法在弯曲倾倒边坡中的应用。Jiang等[44]基于PFC3D介绍了离散元接触黏结模型(novel DEM bond contact model)在节理岩质边坡的应用。岑夺丰等[45]研究了块裂反倾巨厚层状岩质边坡的破坏机制及稳定性。

数值流行方法(NMM)和非连续变形分析(DDA)是石根华于20世纪90年代初提出的数值分析方法[45]。孙东亚等[46]使用DDA验证G-B方法的合理性，指出了G-B法可能出现的问题。张国新等[47-48]将数值流形方法进行扩充，使之能够模拟完整岩体的拉裂与剪断，并且证实了该方法能够很好模拟实际岩质边坡的倾倒破坏。蒋青青等[49]采用FLAC3D中的遍布节理模型分析层理倾角、倾向与边坡稳定性之间的关系。宋彦辉等[50]和王宇等[51]基于强度折减法的节理有限元法(JFEM-SSR)对反倾层状边坡的变形破坏机制进行研究，并应用于实际工程当中。

2.3 试验研究

解析方法的可靠性需要通过试验研究加以验证。对倾倒边坡的试验研究主要有倾斜台面模型试验、基底摩擦试验和离心模型试验三类。

Ashby[3]、Whyte[52]和Soto[53]进行过一系列倾斜台面的模型试验。Wong等[54]开发了一个三维倾斜试验台，可以在模型侧面施加不同的压力。Amini等[55]在其理论研究的基础上，运用倾斜试验台模拟了岩质边坡的块体—弯曲倾倒破坏。Bray等[56]利用基底摩擦试验台研究该问题，用模型与砂纸间的摩擦力来模拟块体的体积力。Steward等[57]、汪小刚等[58]介绍了利用离心模型试验设备展开的研究工作。

一些学者以开挖作为“触发因素”模拟边坡的失稳。左保成等[59]、卢增木等[60]利用相似模型试验，研究岩层的倾角、厚度、结构面强度对反倾层状边坡稳定性的影响，结果显示此类边坡的变形破坏过程具有明显的“叠合悬臂粱”的特征。

对倾倒边坡动力特性的研究主要是振动台模型试验。Aydan等[61]模拟动荷载作用下主动(active)与被动(passive)弯曲倾倒的破坏。杨国香等[62]研究地震作用下反倾层状结构岩质边坡动力响应特征及破坏过程。

3 基于力矩平衡的弯曲倾倒模型

孙广忠认为倾倒变形由以下两个过程组成：(1)在自重作用下板裂体产生弯折；(2)折断点连贯成面，上覆岩体在重力作用下产生滑动或溃屈，最后导致边坡破坏。基于力矩平衡提出了反倾的板裂体弯曲倾倒折断的条件为：在自重和传递力作用下岩块产生的倾覆力矩MT大于内部摩擦力产生的抵抗力拒Mr。

MT>Mr

(1)

其力学模型如图7所示，对A点取矩可得：

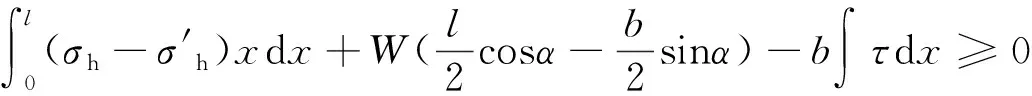
(2)

τ——岩柱侧面的切向应力；

W——岩柱重量；

l、b——分别为岩柱的长度和宽度；

α——岩柱倾角。

弯折破坏的判据为：

σT=[σT]

(3)

式中：[σT]——岩柱的抗拉强度；

σT——岩柱内的拉应力。

(4)

式中：M——岩柱截面内弯矩；

y——中性轴距表面距离；

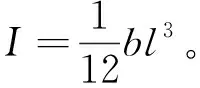
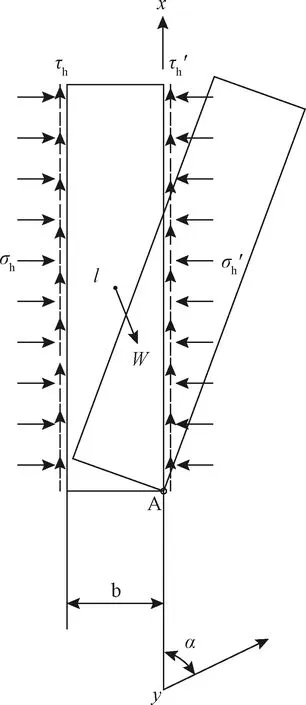
图7 弯曲倾倒力学模型Fig.7 Mechanical model of flexual toppling

孙广忠只是给出了岩柱折断的判据，并没有将其应用于整个的边坡的求解中。基于力矩平衡的思路有别于G-B方法中基于静力平衡的思路。

式(4)中对折断面拉应力的求解公式是针对纯弯曲梁，然而对于叠合梁中考虑侧面摩擦力的情况并不适用，应当加上由于侧面摩擦力而产生的拉应力，如式(5)。

(5)

针对于上述问题，可得：

(6)

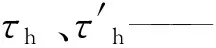
其中，MT、Mr改为对折断面中点取矩：

(7)

(8)

将式(7)和(8)带入式(6)，得到岩柱内拉应力的表达式：

(9)

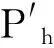
P0<0，边坡稳定；

P0=0，边坡处于极限平衡状态；

P0>0，边坡失稳。

4 讨论与结论

(1) 倾倒破坏是岩质边坡失稳的主要模式，但由于岩层倾倒变形所引起的边坡二次破坏形式有可能是滑动、崩塌等。

(2) 倾倒变形易发生于反倾层状岩质边坡中，但并不等同于其他形式的边坡就不会发生倾倒变形。岩层的长细比较大或岩柱的刚度较小时，易发生向临空面方向的弯曲倾倒；受节理切割的块状岩体或块状—层状互层岩体的失稳模式往往是块体倾倒或块体—弯曲倾倒。顺层陡倾或近直立岩层的边坡，由于层间水压力或冻融作用会形成额外的倾倒力矩，可能会导致边坡的倾倒失稳。次生倾倒模式中，荷载由上部潜在的滑动体传递到下部层状岩体也可能会诱发倾倒失稳。

邱俊等[63]提出层状岩质边坡“倾倒临界倾角δ”的概念。顺倾边坡δ≈60°，当岩层倾角α>δ时，边坡将可能产生倾倒变形；当α<δ时，边坡通常产生顺层面的“滑移-弯曲”或“滑移-拉裂”型破坏。在地质条件基本相同的情况下，反倾边坡演化形成的倾倒体的发育分布面积和倾倒深度通常大于顺倾边坡，反倾边坡形成的倾倒体后缘高程一般在坡肩位置，而顺倾边坡通常会低于坡肩一定高度。

(3) 块体倾倒与弯曲倾倒解析模型最大的不同点是：块体倾倒模型存在已知的破坏面，且假定岩块为刚性体，其本身不发生变形；而弯曲倾倒的潜在破坏面是未知的，岩层可以发生弯曲变形。

大型工程中倾倒边坡的变形多数是弯曲倾倒，合理确定潜在的破坏面对分析边坡的稳定性至关重要。依据地质勘探中岩层倾角和岩体完整性的变化，能够初步推测潜在的倾倒折断面。以往的解析模型基本上是根据模型试验的结果假定破坏面，其准确性和适用性值得进一步探讨。

(4) 目前对倾倒边坡的研究主要集中在稳定性分析方法上，尤其是用数值方法探索此类边坡的变形破坏机理。然而与之相对应的评价方法的研究较少。G-B方法以保证坡脚第一块岩柱稳定所需的抗滑力作为边坡稳定的标志，在实际应用中很不方便。强度折减法较好地弥补了其不足，将计算结果转换成工程中易接受的安全系数。基于考虑倾倒问题中岩柱的抗弯能力，在对剪切强度指标c和tanφ折减的同时，应同时对抗拉强度σt进行折减。

实际工程中遇到的大型高陡边坡越来越多，尤其是倾倒边坡的变形机制较普通滑坡复杂且可预测性差，仅凭一个安全系数的概念不足以判断其安全性，因此建立全面的评价体系至关重要。

(5) 无论是G-B方法还是基于悬臂梁理论的弯曲倾倒模型，在处理该问题时都做了相应的假设，故极限平衡法的适用性有限。有限元法因其平衡方程的连续性，使得在模拟裂隙岩体的大变形受到限制。

离散元克服了有限元法的局限性，使得节理接触的形成和断开、大变形、离散块体的转动和块体变形都很容易实现。结合强度折减的思想，以计算不收敛(设置最大不平衡力控制)作为边坡破坏的依据，在计算中可以通过对应的速度矢量图确定滑动面(破坏面)的位置[64-67]。因此，离散元法适用于各种类型、大小尺度的边坡倾倒变形分析。

(6) 已有的研究大多是基于边坡在自然状态下展开的，较少有涉及到外荷载的影响。但是降雨、库水位变化、开挖卸荷、爆破和地震作用等外荷载影响往往会加剧岩层的倾倒变形，甚至直接导致边坡失稳。针对于这方面的研究将会是今后的重点。