拉压超静定问题中变形协调方程的讨论
2018-07-25张晓艳陈燕唐亮
张晓艳 陈燕 唐亮
摘 要 在材料力学中利用小变形放大法得到变形协调方程是求解杆件拉压静不定问题的重难点。在教学实践中发现,学生往往对杆件拉压受力的定性判断不够准确,导致对杆件力的方向假定不一致以及假设变形长度不同,所得到的变形协调方程也是不同的。现就教科书上针对杆件拉压问题所讲授的变形协调方程的几种形式进行了探讨,在此基础上提出了利用投影法形成变形协调方程简单易于理解,特别是在不易进行拉压定性判断的复杂杆系中更显优势。
关键词 变形协调方程 小变形放大法 材料力学
中图分类号:O347 文献标识码:A DOI:10.16400/j.cnki.kjdkz.2018.05.020
Abstract In the mechanics of materials, the small deformation magnification method is used to obtain the deformation compatibility equation. In the teaching practice, it is found that the qualitative judgment of the tension and compression of the rod is not accurate, which leads to the difference of the assumption that the direction of the rod is not consistent and the length of the deformation is different. In this paper, several forms of the deformation coordination equation are discussed in the textbook for the tension and pressure problem of the rod. On this basis, it is proposed that the formation of the deformation coordination equation by using the projection method is simple and easy to understand, especially in the complex bar system which is not easy to conduct the qualitative judgment of the tension and pressure.
Keywords deformation coordination equation; small deformation amplification method; material mechanics
求解杆件拉压静不定问题一般的解题思路是:[1-4]先建立力学平衡方程,然后根据杆件的变形特点建立变形协调方程,再补充力与变形之间的关系得到补充方程,进而求解得出所有的未知量。为得到变形协调方程,现行材料力学教科书中一般使用都是小变形放大法。
1 现行教材中对小变形放大法的描述
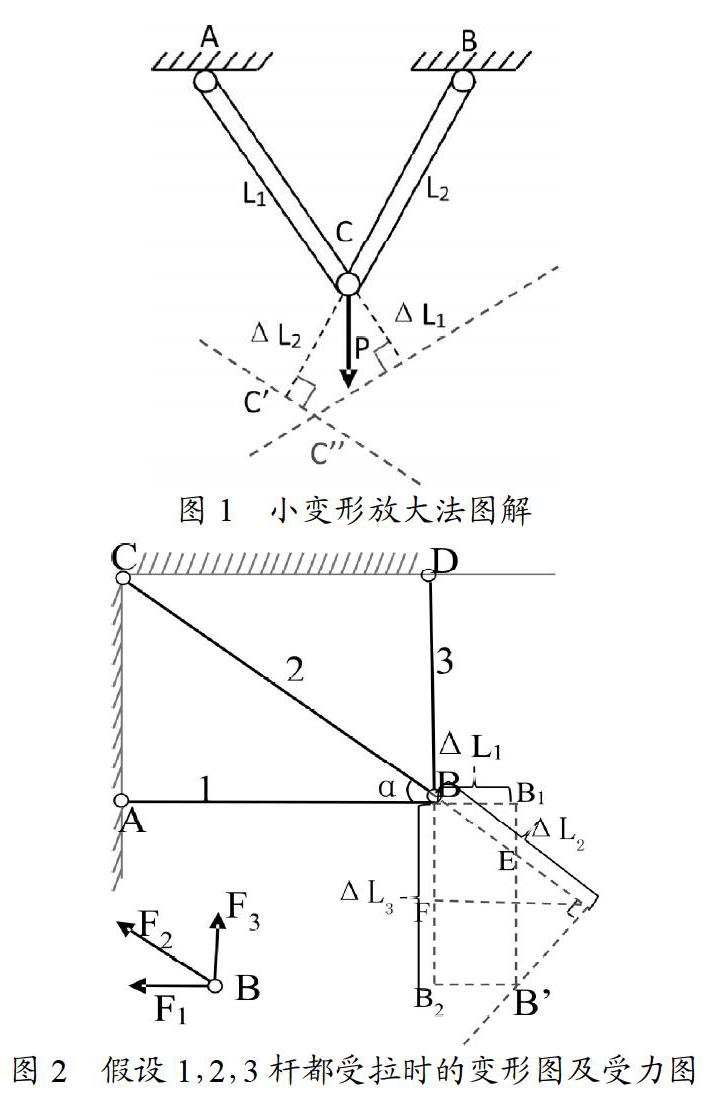
如图1所示,铰接杆件AC、BC在C点受力P的作用,求解C点变形后的位置。利用小变形放大法求解是通过杆件AC和BC伸长量 L1和 L2得到C点水平和竖直方向的位移。变形分析时严格的画法是分别以A点为圆心,(L1+ L1)为半径作圆弧,及以B点为圆心,(L2+ L2)为半径作圆弧,两圆弧的交点C'即为C点变形后的位置。实际操作时常采用的是“以直代曲”的近似畫法,即:分别过AC和BC变形延长线终点做AC和BC的垂线,两条垂线的交点C''就是C点变形后的位置。[5-6]随后,通过求解直角三角形可得到C点的水平和竖直方向的位移。
而在教学实践中发现,学生往往对杆件拉压受力的定性判断不够准确,导致对杆件力的方向假定不一致以及假设变形长度不同,所得到的变形协调方程也是不同的。
如下面的超静定例子。1,2,3杆在B点铰接,利用小变形放大法先画出B点变形后的点B'。当假定3根杆件都受拉时变形图及受力图如图2所示。
通过该变形图(图2)可以得:
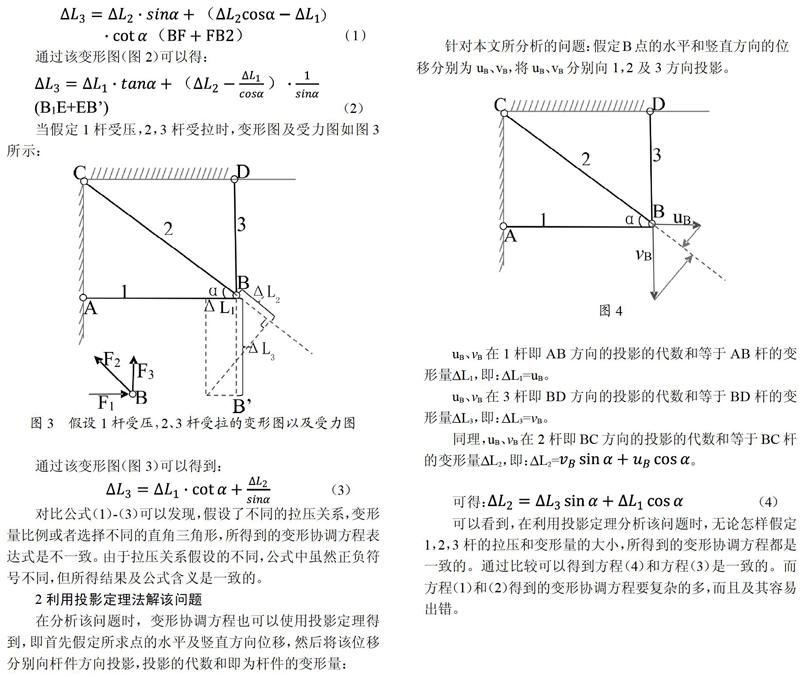
当假定1杆受压,2,3杆受拉时,变形图及受力图如图3所示:
通过该变形图(图3)可以得到:
对比公式(1)-(3)可以发现,假设了不同的拉压关系,变形量比例或者选择不同的直角三角形,所得到的变形协调方程表达式是不一致。由于拉压关系假设的不同,公式中虽然正负符号不同,但所得结果及公式含义是一致的。
2 利用投影定理法解该问题
在分析该问题时,变形协调方程也可以使用投影定理得到,即首先假定所求点的水平及竖直方向位移,然后将该位移分别向杆件方向投影,投影的代数和即为杆件的变形量:
针对本文所分析的问题:假定B点的水平和竖直方向的位移分别为uB、vB,将uB、vB分别向1,2及3方向投影。
uB、B在1杆即AB方向的投影的代数和等于AB杆的变形量 L1,即: L1=uB。
uB、B在3杆即BD方向的投影的代数和等于BD杆的变形量 L3,即: L3=B。
同理,uB、B在2杆即BC方向的投影的代数和等于BC杆的变形量 L2,即: L2=。
可得: (4)
可以看到,在利用投影定理分析该问题时,无论怎样假定1,2,3杆的拉压和变形量的大小,所得到的变形协调方程都是一致的。通过比较可以得到方程(4)和方程(3)是一致的。而方程(1)和(2)得到的变形协调方程要复杂的多,而且及其容易出错。
3 结束语
现行教材中求解杆件拉压的静不定问题使用小变形放大法时,对于复杂的杆件组(超过2个杆件),定性分析杆件受拉或受压,或假设的杆件变形量相对大小不同作图时,作图所得到的变形后的点会不同,造成的结果是所列变形协调方程也会不同,增加了解题的难度以及理解问题的复杂度。投影定理法在理解问题上概念清晰,求解过程都简单明了,所形成的变形协调方程易于理解,特别是在不易进行拉压定性判断的复杂杆系中更显优势。
参考文献
[1] 孙训方,方孝淑,关来泰.材料力学(1).北京:高等教育出版社(第5版),2009.
[2] 刘鸿文.材料力学(1).北京:高等教育出版社(第6版),2017.
[3] 单辉祖.材料力学(1).北京:高等教育出版社(第4版),2016.
[4] 盖尔(James M. Gere),古德诺(Barry J. Goodno).材料力学.北京:机械工业出版社(翻译版, 原书第8版),2017,
[5] 邓宗白,陶秋帆,金晖.关于材料力学中小变形问题的讨论[J].力学与实践,2009.31(4):72-76.
[6] 常学平,王维,蒋平,等.拉、压静不定问题变形几何分析中存在的问题[J].力学与实践,2008.30(2):89-90.
